执行器饱和受限系统的鲁棒控制及其在网络遥操作机器人系统中的应用

姚合军，杨 恒

(安阳师范学院 数学与统计学院，河南 安阳 455000)

0 引言

饱和现象在实际控制系统是最常见的现象，本质上任何系统都有不同程度的饱和约束，如果不考虑饱和限制，那么严重情况下将导致系统性能下降甚至不稳定。在实际工程控制过程中，执行器饱和是一种最为常见的约束，因此有关执行器饱和控制的研究具有非常重要的实际意义。

上世纪60年代Fuller首次提出饱和系统，并采用回馈计算和跟踪的策略，使系统快速退出饱和区。近几十年来，执行器饱和控制问题得到了众多学者的广泛关注[1-3]。Hu等人提出了一种在饱和线性反馈下估计离散线性系统吸引域的方法和一种基于LMI的方法来构造具有保证稳定性要求的干扰抑制反馈律[4]。魏爱荣等人针对执行器饱和的状态反馈单输入线性系统和输出饱和的动态输出反馈单输出线性系统，给出了保证全局渐近稳定或区域渐近稳定的充分条件[5]。王茂等人基于一个参数相关的不连续切换Lyapunov函数和一些基本引理，设计一个能保证闭环系统局部指数稳定的开关静态输出反馈控制器[6]。Zuo等人利用线性矩阵不等式方法给出了执行器饱和的线性系统吸引域估计[7]。接着，Zhou等人把饱和系统的设计方法引入到饱和网络控制系统中来，研究了饱和网络系统的输出反馈镇定问题[8]。李金娜等人利用Lyapunov方法，给出了具有饱和非线性约束的网络控制系统鲁棒稳定性的充分条件。然后，给出了γ次优和最优鲁棒H∞控制的充分条件[9]。张美玉等人利用线性矩阵不等式方法设计了非线性执行器饱和时滞切换系统的状态反馈控制问题[10]。陈东彦等人通过迭代算法对饱和时滞系统进行吸引域估计，并讨论了系统的全局渐近稳定性问题[11]。然而上述文献对饱和系统的研究过程中所设计的Lyapunov函数缺少恰当的参数矩阵，所得结果具有较大的保守性，另外都没有考虑到外界干扰或不确定性对系统的影响。正因为此,在前人研究的基础上，针对执行器饱和受限的不确定系统，利用线性矩阵不等式方法探寻系统稳定的充分条件，降低该条件的保守性是有意义的。

1 问题描述

考虑如下执行器饱和受限的不确定时延系统

(1)

x(t)=φ(t)t∈[-d,0]

其中x(t)∈Rn是状态向量，u(t)∈Rm是控制输入向量，A,Ad∈Rn×n，B∈Rn×m是已知的常数矩阵，φ(t)=[φ1(t)φ2(t)…φn(t)]T∈Rn是给定的系统初始状态，d是系统状态时延，饱和函数sat(u(t))=[sat(u1(t)),sat(u2(t)), …,sat(um(t))]，其中

ΔA(t),ΔAd(t),ΔB(t)是具有适当维数的系统不确定性，满足

[ΔA(t),ΔAd(t),ΔB(t)]=DF(t)[E1,E2,E3]

(2)

其中矩阵函数F(t)满足FT(t)F(t)≤I

设计系统(1)的状态反馈控制器：

u(t)=2Kx(t)

(3)

其中K∈Rm×n是待定的常数矩阵。把(3)代入系统(1)中得到闭环系统

(4)

x(t)=φ(t)t∈[-d,0]

其中

η(t)=sat(2Kx(t))-Kx(t)

(5)

并且η(t)满足

ηT(t)η(t)≤xT(t)KTKx(t)

(6)

设计目的是确定形如(3)的控制器，使闭环系统(4)是渐近稳定的。

2 主要结果

引理1[12]如果对具有适当维数的矩阵Y,D和E，对称矩阵Y，以及满足FTF≤I的矩阵F，则不等式Y+DFE+ETFTDT<0成立，当且仅当存在一个常数ε>0，使得

Y+εDDT+ε-1ETE<0

定理1如果存在正定矩阵P，Q∈Rn×n,矩阵K∈Rm×n以及ε>0，使得下面矩阵不等式

H(t)=

(7)

成立，则闭环系统(4)是渐近稳定的。

证明选取带有参数矩阵的Lyapunov函数如下

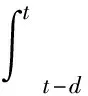
P,Q∈Rn×n是待定的对称正定矩阵。

V(t)沿系统(4)求导得到

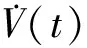
-xT(t-d)Qx(t-d)

(8)

其中

由(6)式得到

其中ε是任意小的一个正数。

把上式带入(8)式得到

由条件(7)可知闭环系统(4)是渐近稳定的。

定理1中的条件(7)不是线性的，不能用MATLAB求解，下面我们利用恰当的矩阵变换把条件(7)转化为线性的矩阵不等式。

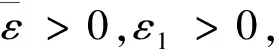
(9)

证明由引理1可知不等式(7)等价于

上式左右两边分别乘以分块对角矩阵diag{P-1,P-1,ε-1I,ε-1I}得到：

把式(5)带入上式得

其中

由引理1知，上式当且仅当存在ε1>0时，下面式子成立

由Schur引理，易知上式等价于式(9)。

3 数值算例

图1 移动机器人物理模型

本部分内容将对如图1并受远程遥操作的移动机器人系统进行模拟仿真。假设移动机器人的质量为M，转动惯量为Iv，左右轮的轮间距为l，机器人移动线速度为v，机器人方位角为φ，轮的转动惯量Iw，k为驱动增益，r为轮子的半径，θl,θr分别为左轮和右轮的转动的角，ul,ur分别为左右轮的驱动输入，c为机器人和地面间的摩擦系数，经动力学分析可得机器人的动力学模型为

其中

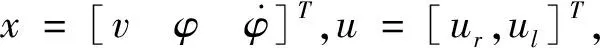
其中

考虑到系统可能会受到不确定外界干扰和系统传输时延以及控制器饱和的影响，考虑如下形式的机器人系统

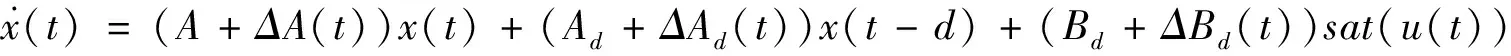
x(t)=φ(t)t∈[-d,0]

其中

d=0.1,执行器饱和函数sat(u(t))=[sat(u1(t)),sat(u2(t))]满足

解线性矩阵不等式(9)得到控制器为

选取初始状态为

则闭环系统状态响应图如下：

图2 状态x1(t)的响应图

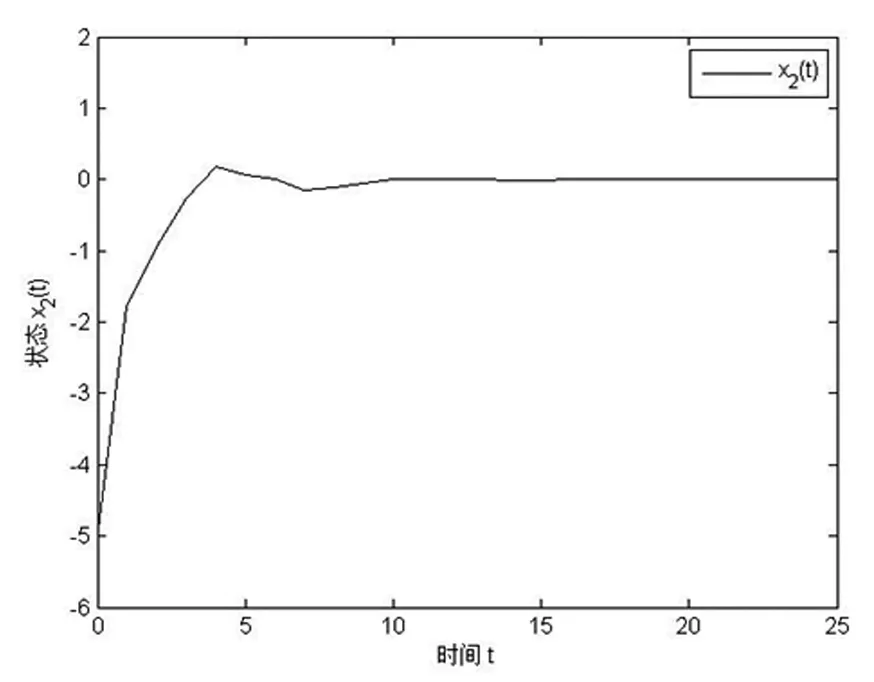
图3 状态x2(t)的响应图

由图2、图3容易看出该机器人系统状态收敛速度较快，状态曲线振幅较小，平稳性较好，系统整体性能较优。

4 结论

本文给出了一类带有执行器饱和项和时延的不确定系统的渐近稳定条件和鲁棒控制设计方法，通过增加系统维数消除饱和项，在Lyapunov函数中引入参数矩阵，降低了系统渐近稳定条件的保守性，并把所得方法应用到了网络遥操作机器人系统。