高功率掺Tm3+自相似脉冲激光器的仿真优化设计

石郑楠延凤平韩文国张鲁娜

(北京交通大学光波技术研究所全光网络与现代通信网教育部重点实验室，北京 100044)

1 引 言

超短脉冲在生物医学、塑料加工以及光通信等领域有着重要应用[1-3]，近几十年引起了广泛的研究兴趣。锁模光纤激光器可以产生皮秒量级或者飞秒量级的超短光脉冲，但是由于孤子面积定理和频谱边带的限制使得锁模激光器产生的孤子能量通常小于0.1 nJ[4-7]。为了获得更高能量的超短脉冲，研究人员关注到了自相似脉冲锁模光纤激光器。1993年，Anderson等[8]最早在求解用来描述光纤中光脉冲的传输特性的非线性薛定谔方程时发现了自相似光脉冲的存在。这一研究极大地激发了研究人员探究自相似脉冲的兴趣。2004年，Ilday等[9]提出了一种掺镱自相似脉冲光纤激光器，仿真模拟了激光器中自相似脉冲的演化过程，并且获得了能量为10 nJ的脉冲。2014年，Liu等[10]报道了一个掺铒自相似光纤激光器，发现了在增益光纤中具有自相似脉冲的演化。该激光器产生了3.5 nJ的脉冲，并通过外部光栅对将脉冲降低至70 fs。

与掺镱和掺铒增益光纤相比，掺铥光纤表现为异常色散。并且掺铥光纤激光器在肿瘤切割、激光手术刀、塑料材料切割等领域有着独特的应用，因此在2 μm波段获得超短脉冲具有重要意义。2015年，Tang等[11]报道了一种基于可变正常色散的掺铥锁模光纤激光器。从理论和实验上分别证实了在正常色散较大时，该激光器具有自相似脉冲演化的特性，并且是第一款能够实现正常色散操作的高性能掺铥光纤激光器。该激光器产生了7.6 nJ的脉冲，并可以将脉宽降低至130 fs，产生的峰值功率是以前的掺铥光纤激光器峰值功率的4倍。随后，Liu等[12]在该模型的基础上，利用数值模拟方法对掺铥光纤激光器中色散管理的高能自相似脉冲进行了优化设计。最终，通过增加腔长、泵浦功率以及滤波器带宽等方法获得了能量高达32.75 nJ、脉宽为142.64 fs的脉冲。由于材料的限制，大多数有关色散管理的报道仍集中在1.55 μm波段，很少有报道涉及2 μm波段。目前，激光器环形腔中已使用体光栅元件[13]和特殊的正色散光纤[14]来补偿2 μm波段的色散。近年来，许多研究人员还发现，通过减小纤芯直径和增加数值孔径，光纤的零色散波长可以扩展到更长的波长[15]。因此，低成本、易于集成的高数值孔径光纤可用于补偿2 μm波段激光器谐振腔中的色散[16-20]。

虽然掺铥自相似脉冲激光器具有独特应用，但是相关报道并不多。在已有的报道中，所获得的脉冲功率不高，并且用到的光学器件较多，成本较高。鉴于此，本文构建了一种新的较为简单的掺铥锁模光纤激光器模型，并产生了2 μm自相似脉冲。为了获得更高功率的脉冲，对掺铥锁模光纤激光器进行了优化设计，仿真分析了腔内净色散、增益系数和可饱和吸收体等参数对获得高功率自相似脉冲产生的影响，最后通过外部光栅对脉冲进行了压缩。

2 数值模型的建立

2.1 激光器的结构模型

本文中搭建的掺Tm3+自相似脉冲激光器结构如图1所示。激光腔包括：一段掺铥光纤(TDF)、两段单模光纤(SMF)、一段高数值孔径单模光纤(UHNA7)，以及光隔离器(Isolator)、可饱和吸收体(SA)、光纤合束器(FC)和输出耦合器(Coupler)。模型中的TDF作为增益光纤，UHNA7光纤用来进行色散补偿，SA的作用是启动和稳定锁模，Isolator保证光的单向传输。当FC将泵浦光(Pump)耦合进激光器后，光脉冲依次经过光器件进行循环，部分脉冲从Coupler输出，输出采用的是90∶10耦合器，其中10%作为输出端。

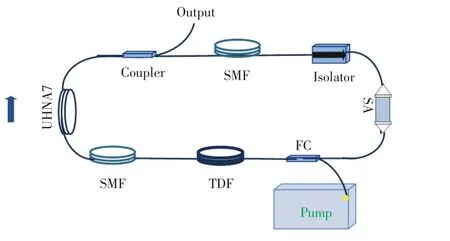
图1 掺Tm3+自相似锁模激光器结构示意图Fig.1 Schematic diagram of the thulium-doped self-similar mode-locked laser

2.2 光纤及器件的数值模型

为了便于分析，本文忽略高阶色散和高阶非线性的影响[21-23]，用来描述脉冲在光纤中传输的数值方程为非线性薛定谔方程[24-25]，如下式：

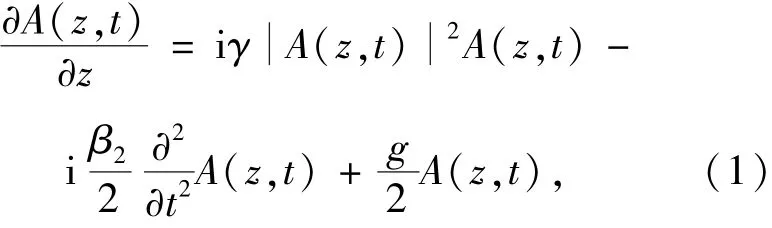
其中，A(z，t)为脉冲包络的慢变振幅，β2为群速度色散系数，γ为非线性系数，g为增益系数。对于掺铥增益光纤，g可用下式表示：

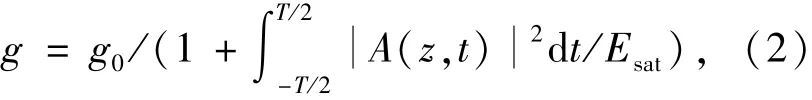
其中，g0为小信号增益系数，Esat为增益饱和能量，T为脉冲在光纤中传输一次的时间。对于单模光纤，g0＝0。

模型中的可饱和吸收体(SA)用来启动和稳定锁模，并能够使脉冲进行窄化，其透射率函数用下式表示：

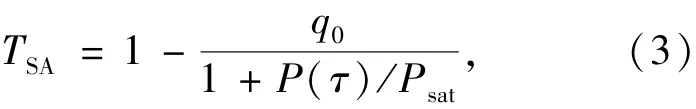
其中q0为可饱和吸收体的调制深度，P(τ)为瞬时功率，Psat为饱和功率。

腔外压缩[26]采用光栅作为色散延迟线(DDL)，其作用是对脉冲提供负色散补偿，DDL可用下式表示：

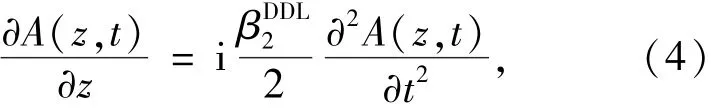
其中，为光栅的色散量。

3 数值仿真结果和分析

自相似脉冲产生于净色散为正且在反常色散器件中无非线性效应的谐振腔内[27]，因此本文通过调节UHNA7光纤的长度来改变腔内净色散的值，以实现激光器输出稳定的自相似脉冲。模拟用到的光纤参数如表1所示。除此之外，可保和吸收体调制深度q0为0.9，饱和功率为9 W。

根据表中参数进行仿真，用一个微小的噪声信号作为初始脉冲。输出脉冲时域演化图如图2所示，从图中可以看出，脉冲在运行约400圈后，输出脉冲基本稳定，脉冲峰值功率为257.5 W，脉冲半高全宽FWHM为30.58 ps。

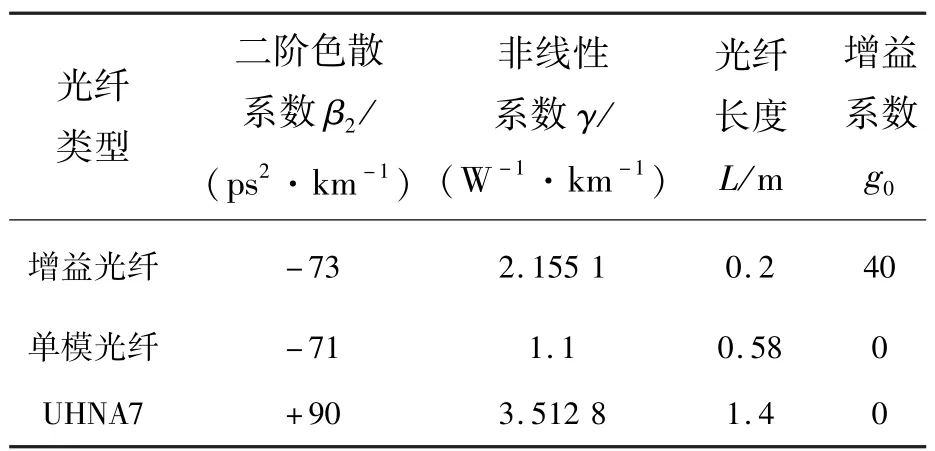
表1 激光器的参数表Tab.1 Laser parameters

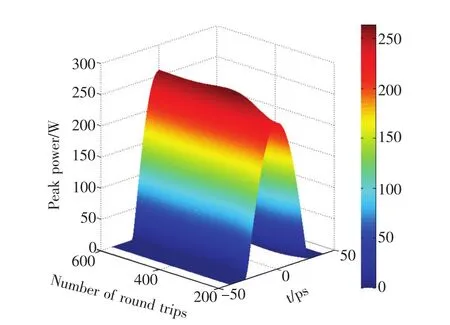
图2 脉冲时域演化图Fig.2 Time domain evolution diagram of pulse

3.1 典型的2 μm自相似脉冲特征

为了定量分析激光器产生的脉冲为自相似脉冲，引入失配参数M2来描述激光器产生的脉冲与理想抛物线之间的关系[28]。失配参数量化了某一时刻脉冲强度2与拟合的抛物线脉冲之间的差异。M2可用公式(5)进行定义：

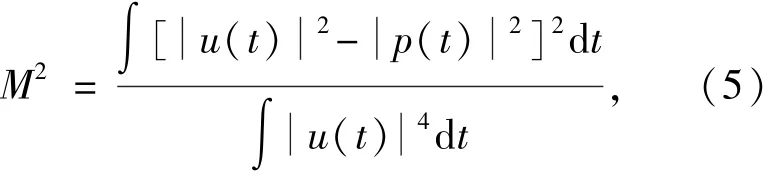
通过缓慢调整腔内净色散的值，激光器输出脉冲形状在发生变化，失配参数M2也在发生变化，脉冲从高斯波形(M＝0.14)演变而来，当M＜0.06时，脉冲波形被认定为抛物线型[29]。此外，腔内净色散值由LUHNA7决定。由腔内净色散与失配参数之间的关系(图3)可知，腔内净色散值在0.02～0.08 ps2时，M＜0.06，此时脉冲波形为抛物线脉冲；在腔内净色散值为0.033 ps2时，M值最小为0.018，证明演化脉冲与抛物线脉冲拟合较好。

图4(a)为 Δβ2＝0.033 ps2时，激光器输出时域自相似脉冲与对应的啁啾曲线图。从图中可以看出，激光器输出脉冲峰值功率为257.5 W，脉冲半高全宽为30.58 ps，对应的脉冲能量约为7.87 nJ，并且伴随着严格的线性正啁啾。这是由于腔内总体色散呈现正色散导致的，这一现象对后续进行脉冲压缩有很大的优势。图4(b)所示为脉冲频域波形图，可以看出脉冲线宽约为26 nm，并且脉冲频域波形同样类似于抛物线型。

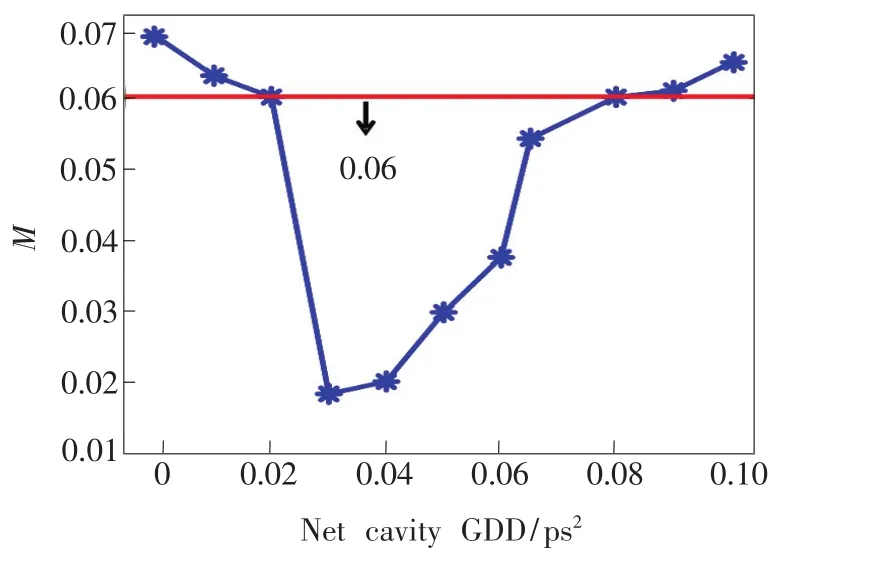
图3 腔内净色散与M关系图Fig.3 Relationship between net dispersion and M

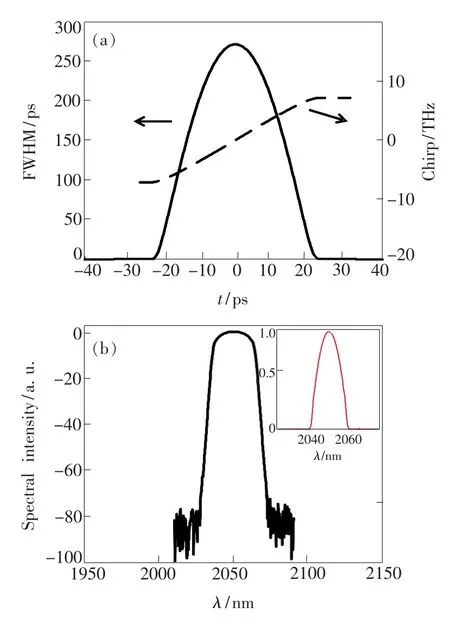
图4 (a)输出脉冲时域图；(b)频域脉冲曲线图。Fig.4 (a)Time domain diagram of output pulse.(b)Pulse diagram in frequency domain.

3.2 腔内净色散对2 μm自相似脉冲的影响

由上文的仿真分析可知，腔内净色散值在0.02～0.08 ps2时，输出的2 μm脉冲为稳定的抛物线型脉冲。因此本论文在0.02～0.08 ps2这一范围内分析随着腔内净色散值的变化，自相似脉冲输出特性的变化情况。仿真过程中通过调整UHNA7光纤的长度来改变腔内净色散的值，其他参数均与表1一致。仿真结果如图5(a)、(b)所示。

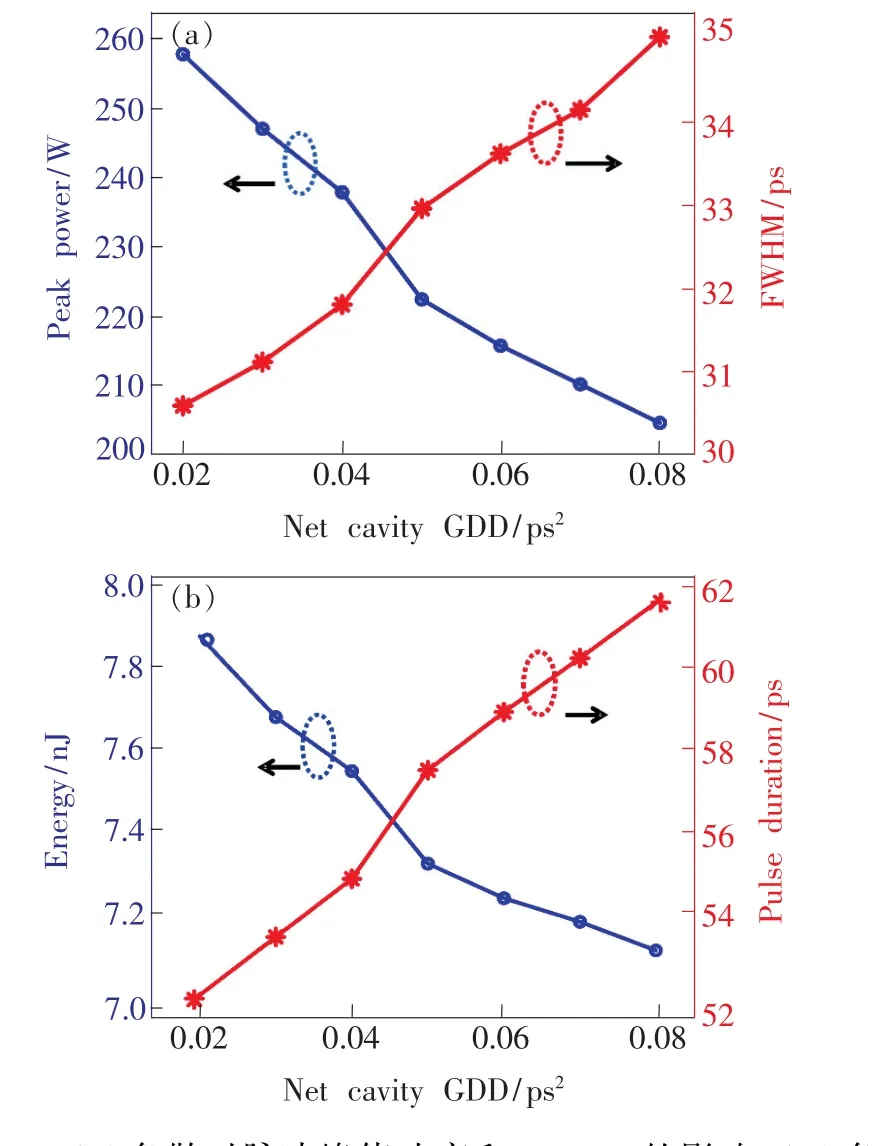
图5 (a)色散对脉冲峰值功率和FWHM的影响；(b)色散对脉冲光持续时间和能量的影响。Fig.5 (a)Effect of dispersion on peak power and FWHM.(b)Effect of dispersion on pulse duration and single pulse energy.

由以上分析可知，当腔内净色散值在0.02～0.08 ps2范围内变化时，脉冲的峰值功率、半高全宽、单脉冲能量和脉冲持续时间都会随之改变。

随着腔内净色散的增加，脉冲峰值功率和单脉冲能量在降低，而脉冲时域半高全宽和脉冲持续时间在增大。由于色散增加使得脉冲时域宽度发生展宽，从而降低了脉冲峰值功率，又因为脉冲峰值功率的降低，导致可饱和吸收体对脉冲的吸收效应变得不明显，这会引起腔内损耗的增加，从而使得单脉冲能量有所降低。由此可知，在一定的腔内净色散范围内，可通过适当降低腔内净色散的值来获得高功率、窄脉宽的2 μm自相似脉冲。

3.3 增益系数对2 μm自相似脉冲的影响

以下仿真是在腔内净色散值为0.033 ps2时进行的。由公式(2)可知，小信号增益系数和增益系数成正比，因此，可用小信号增益系数g0代替增益系数进行仿真。仿真过程中保持其他参数不变，只改变小信号增益系数，经仿真模拟可知，g0在40～46 m-1范围内可输出稳定的自相似脉冲。因此在这一范围内进行分析，仿真结果如图6(a)、(b)所示。随着小信号增益系数的增加，无论是脉冲峰值功率、FWHM、单脉冲能量还是脉冲持续时间，都随着g0的增加而线性增加。g0的增加导致脉冲峰值功率随之增加，出现这一现象是因为脉冲能量的增加引起的。仿真过程中非线性效应与群速度色散所占的主导位置是不同的，脉冲FWHM和脉冲持续时间的增加主要是因为在激光腔内色散效应占主导地位，随着g0的增加，在谐振腔内非线性效应的提升可以产生更宽的频谱，从而引起脉冲时域FWHM和脉冲持续时间增加。

图6 (a)g0对峰值功率和FWHM的影响；(b)g0对脉冲能量和脉冲持续时间的影响。Fig.6 (a)Effect of g0on peak power and FWHM.(b)Effect of g0on pulse energy and pulse duration.

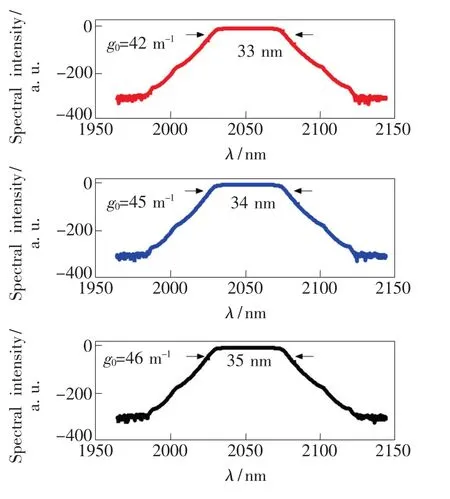
图7 g0对脉冲光谱带宽的影响Fig.7 Effect of g0on pulse spectral bandwidth

虽然g0引起输出特性发生改变，但是脉冲形状并没有因此而改变，该结果表明激光器输出脉冲形状与小信号增益系数无关，并且要想提高脉冲能量可通过适当增加g0来获得。

图7为g0对脉冲光谱宽度的影响，可以看出脉冲光谱有明显的变化趋势，从33 nm增加到了35 nm，这一过程是由于在谐振腔内非线性效应的提升而引起的。

3.4 SA对2 μm自相似脉冲的影响

SA对实现脉冲的锁模和稳定具有决定性作用，而SA特性可由其自身的调制深度q0和饱和功率等属性所决定。因此，接下来采用控制变量法分析SA的调制深度和饱和功率对2 μm自相似脉冲的影响。

首先研究了SA的调制深度对脉冲的影响。保持掺铥锁模光纤激光器中其他参数不变，只改变SA的调制深度，通过仿真分析可知，调制深度在0.3～0.9范围内变化时可实现脉冲锁模，因此在这一范围内对脉冲的输出特性进行分析。仿真结果如图8(a)、(b)所示。

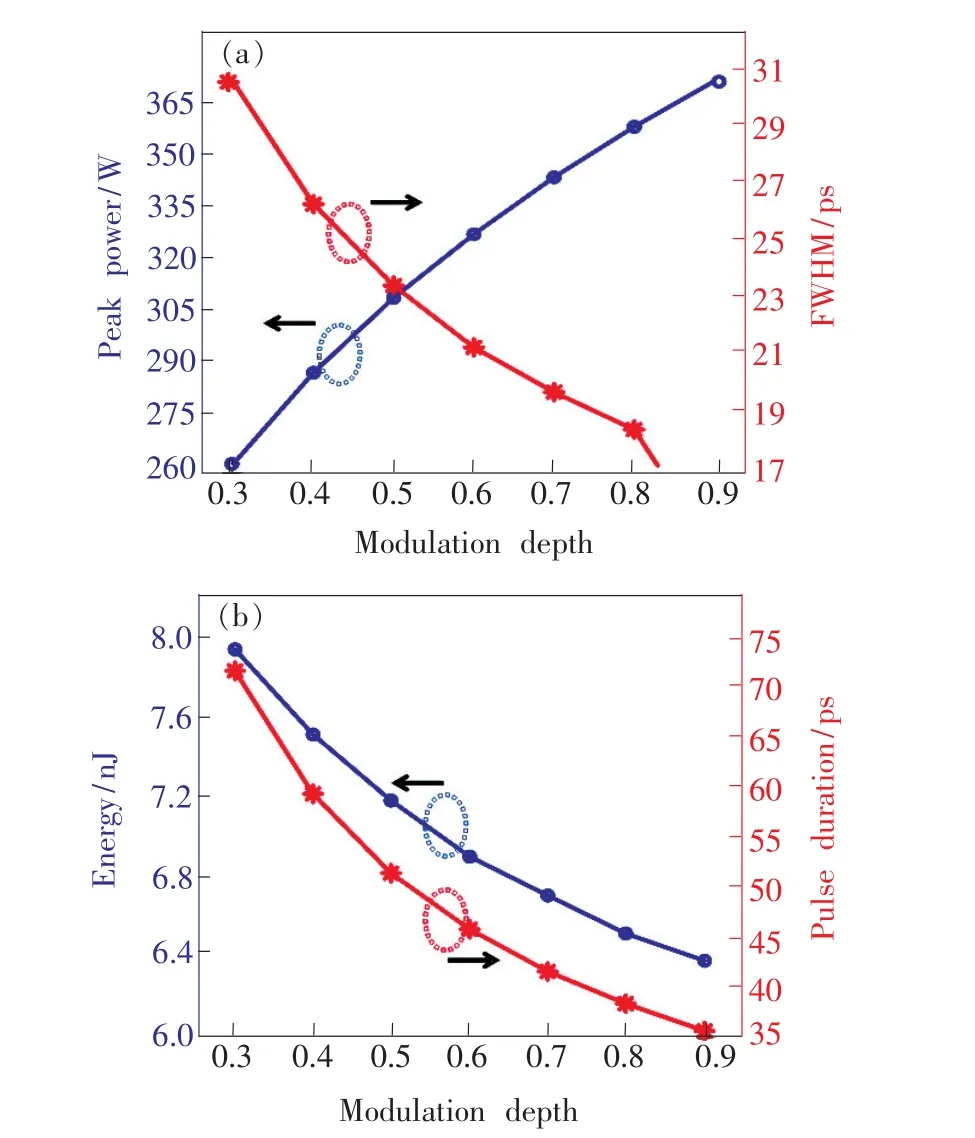
图8 (a)q0对峰值功率和FWHM的影响；(b)q0对脉冲能量和持续时间的影响。Fig.8 (a)Effect of q0on peak power and FWHM.(b)Effect of q0on pulse energy and pulse duration.

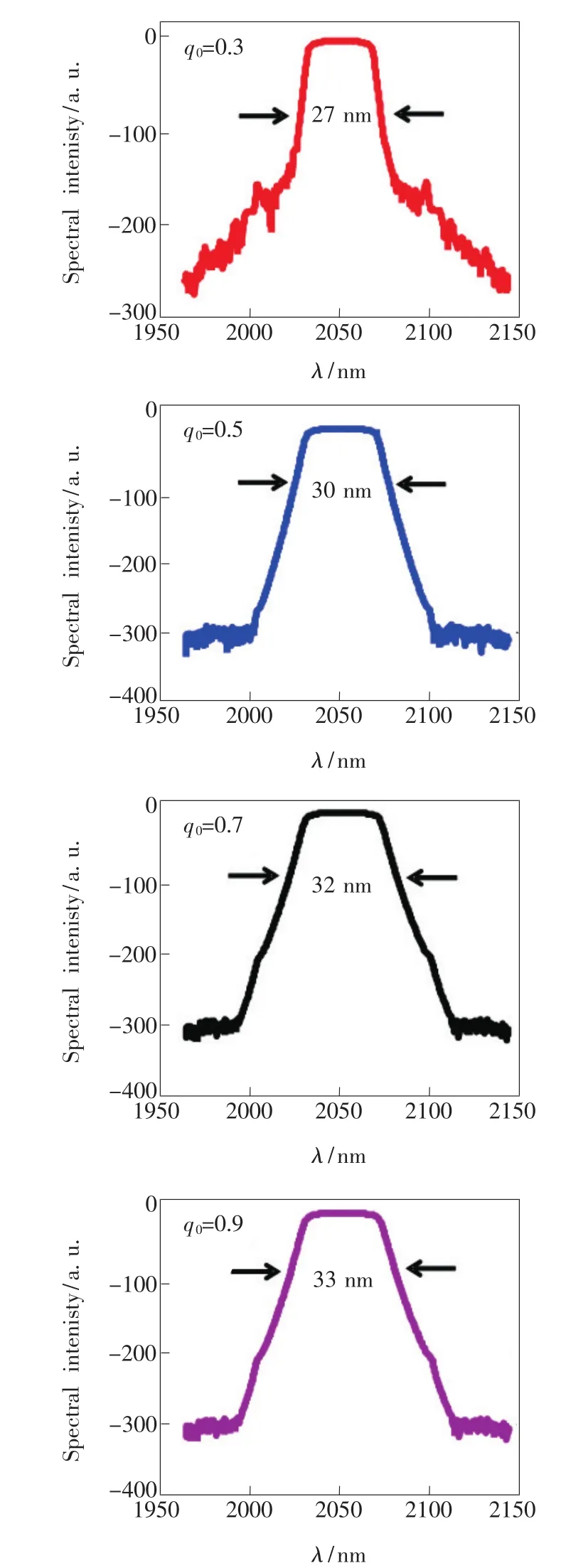
图9 q0对脉冲光谱带宽的影响Fig.9 Effect of q0on pulse spectral bandwidth

由图8可以看出，随着调制深度的增加，脉冲峰值功率增加，而脉冲FWHM、单脉冲能量和脉冲持续时间都随着调制深度的增加而减小。较高的调制深度会增加可饱和吸收体的吸收效应，从而使脉冲窄化效果更明显。而单脉冲能量降低的原因是在泵浦功率固定的情况下，较高的调制深度意味着更多的损耗，从而导致腔内单脉冲能量的减小和非线性相移的增加。非线性效应的增加会导致脉冲频谱宽度的增加，不同调制深度下脉冲频谱比对图如图9所示。由图中还可以看出，随着调制深度从0.3增加到0.9，输出频谱中陡峭的频谱边缘逐渐减弱，这归因于线性啁啾的频率降低。从以上仿真结果可以看出，设计不同的可饱和吸收体的调制深度，能够达到不同的效果。

由以上分析可知，当SA的调制深度为0.9时，可获得高功率、窄脉宽的自相似脉冲，因此，固定调制深度为0.9保持不变，接下来研究可饱和吸收体的饱和功率Psat对2 μm自相似脉冲的影响。经仿真分析可知，在所构建的模型中，饱和功率在5～100 W之间可输出稳定的脉冲。因此，分析饱和功率Psat对脉冲峰值功率、FWHM、单脉冲能量及脉冲持续时间等输出特性的影响在这一范围内进行。仿真输出结果如图10(a)、(b)所示。结果表明，脉冲峰值功率随着饱和功率的增加呈指数型增加，而单脉冲能量和脉冲FWHM以及脉冲持续时间随着饱和功率的增加呈指数型下降，在饱和功率大于75 W时，随着饱和功率的增加，脉冲能量和脉冲时域FWHM基本保持稳定。由图11可以看出，在低饱和功率时，脉冲光谱宽度在缓慢增加，而在高饱和度时，输出脉冲频谱FWHM也基本保持恒定。在低饱和功率下可以获得较高的脉冲能量，而在高饱和功率的条件下，能够获得较高的峰值功率和较窄的脉冲宽度。因此，适当地选择SA的饱和功率对产生高功率、窄脉冲的自相似脉冲有很大的影响。

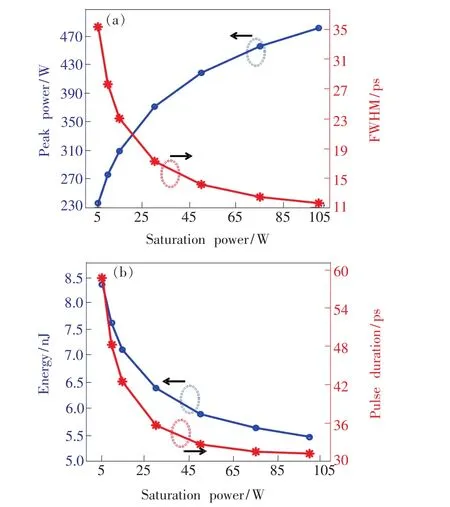
图10 (a)Psat对峰值功率和FWHM的影响；(b)Psat对脉冲能量和持续时间的影响。Fig.10 (a)Effect of Psaton peak power and FWHM.(b)Effect of Psaton pulse energy and pulse duration.

图11 Psat对脉冲光谱宽度的影响Fig.11 Effect of Psaton pulse spectral bandwidth

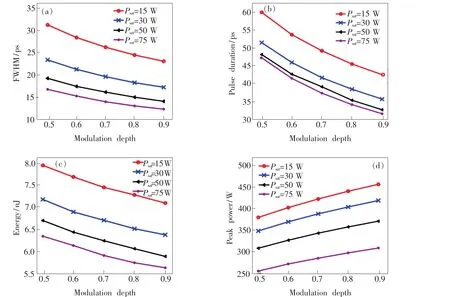
图12 (a)不同q0和Psat对FWHM的影响；(b)不同q0和Psat对脉冲持续时间的影响；(c)不同q0和Psat对脉冲能量的影响；(d)不同q0和Psat对峰值功率的影响。Fig.12 (a)Effect of different q0and Psaton FWHM.(b)Effect of different q0and Psaton pulse duration.(c)Effect of different q0and Psaton pulse energy.(d)Effect of different q0and Psaton peak power.

为了清楚地显示SA参数对激光器输出2 μm自相似脉冲特性的影响，仿真分析了在不同的调制深度下使用不同的饱和功率对输出脉冲产生的影响。图12(a)所示为不同饱和功率下输出脉冲宽度与调制深度之间的关系。该图表明，使用高饱和功率和高调制深度的SA可以获得较窄的脉冲。此外，当饱和功率大于50 W时，脉冲持续时间变化很小，如图12(b)所示。图12(c)显示了不同饱和功率下，调制深度从0.5到0.9变化时的输出脉冲能量的变化情况。在饱和功率固定的情况下，随着调制深度的增加，输出的单脉冲能量在减小。此外，对于给定的调制深度，较高的饱和功率会导致较低的脉冲能量。从图中还可以看出，如果输出脉冲能量保持恒定，则较高的调制深度对应于较低的饱和功率。图12(d)展示了脉冲峰值功率在不同饱和功率、不同调制深度之间的变化，由图中可以看出，随着调制深度和饱和功率的同时增加，脉冲峰值功率随之增加。因此，较高的饱和功率和调制深度有利于获得高峰值功率的脉冲。

由以上分析可知，可饱和吸收体SA的相关参数极大地影响了掺Tm3+锁模光纤激光器的性能。特别地，调制深度和饱和功率的变化会造成明显的脉冲能量和脉冲持续时间的变化。适当地选择可饱和吸收体对在2 μm波段产生高功率、窄脉宽的自相似脉冲有很大影响。

3.5 2 μm自相似脉冲压缩

采用光栅对产生的2 μm自相似脉冲进行压缩，仿真过程中，光栅色散系数为-71 ps2/km，光栅提供了一种负色散，起到色散补偿作用。通过改变光栅的色散量实现对脉冲的压缩。图13所示为压缩前后的脉冲对比图，其中黑色和红色曲线分别表示压缩前和压缩后的脉冲。压缩后的脉冲峰值功率为20.85 kW，脉宽为547.4 fs。

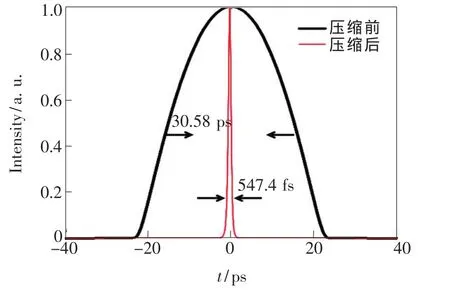
图13 压缩前后脉冲对比图Fig.13 Comparison of pulses before and after compression

4 结 论

本文建立了一个掺Tm3+锁模光纤激光器的数值模型，模拟了2 μm波段自相似脉冲在激光器中的运行状态，从激光器中输出了能量为7.87 nJ、脉宽为30.58 ps的2 μm自相似脉冲。研究发现，腔内净色散在0.02～0.08 ps2范围内时，可产生稳定的自相似脉冲。同时，适当降低腔内净色散能够提高脉冲的输出能量以及降低脉冲的FWHM；基于所构建的模型，当腔内净色散值为0.033 ps2时，小信号增益系数在40～46 m-1范围内可产生稳定的脉冲；随着增益系数的增加，脉冲峰值功率、FWHM以及脉冲能量都随之增加；随后仿真分析了可饱和吸收体的调制深度和饱和功率对自相似脉冲产生的影响，通过分析可知，适当增加SA的调制深度和饱和功率能够得到高功率、窄脉宽的自相似脉冲。因此，为了获得高功率的自相似脉冲，需要全方面考虑系统的各个参数。最后，对产生的2 μm自相似脉冲进行了压缩，经过腔外光栅压缩获得了峰值功率为20.85 kW、脉宽为547.4 fs的脉冲。本文为获得高功率的自相似脉冲进行了优化，同时为后续研究者提供了指导和建议。