Sr2MgSi2O7中本征缺陷和镧系离子的热力学稳定性和转变能级

闻 军,汪 燕,江贵生,郭 海,宁利新

(1.安庆师范大学电子工程与智能制造学院，安徽安庆 246133；2.安徽师范大学功能分子固体教育部重点实验室，安徽芜湖 241000；3.安徽师范大学光电材料科学与技术安徽省重点实验室，安徽芜湖 241000； 4.浙江师范大学物理系，浙江金华 321004)

1 Introduction

The phosphor Sr2MgSi2O7(SMSO)∶Eu2+，Dy3+is a kind of important long-afterglow material and has many advantages， such as the long afterglow time，high stabilities，non-radiation and so on.Since around 2001[1]，researchers have extensively studied this phosphor[1-12]，in order to determine the luminescent and trap centers，understand mechanisms of the thermoluminescence(TL)and long-lasting luminescence(LLL)，and improve its luminescent properties.It is known that the SMSO∶Eu2+，Dy3+exhibits a broadband emission，which is ascribed to the electronic transitions from the excited 4f65d1to the 4f7states of Eu2+ions.Besides，the co-doping of Dy3+ions would enhance the emission intensity，but not affect the position of the emission band.

As for the roles of native defects(anion and cation vacancies)and co-doped lanthanide ions(Dy3+，La3+，Ce3+，Er3+and so on)in the TL and LLL of the material，not only the experimental measurements[1-7]but also the theoretical calculations[8-12](such as the first-principles and empirical methods)are carried out.It is important to note hereby that the previous first-principles studies on the defective and lanthanide-doped SMSO usually identify the levels related to electron and hole traps according to the Kohn-Sham states from the calculations on band structures or the density of states(DOSs).However，these states should not be confused with the optical transition levels between the different charge states of the same defect/dopant[13]，whose locations in the host band gap correspond to trap depths determined from the experimental TL curves of the long afterglow material.

In the present work，hybrid density functional theory(DFT)calculations on formation energies and transition levels of native defects，defect complexes and lanthanide ions in the SMSO are performed in order to theoretically assign the origins of electron traps in the SMSO∶Eu2+，Dy3+.The calculated formation energies reveal the relatively easily generated defects，whose thermodynamic and optical transition energy levels are further derived.The energy differences between the conduction band minimum(CBM)and the two types of defect levels above respectively give the energies of zero-phonon lines(ZPLs)and electronic transitions for the processes of the electron exchange between native defects(or lanthanide dopants)and the CBM.It is found from this study that the thermodynamic and optical transition energy levels corresponding to the oxygen vacancies with the negative charge states are very close to the CBM.Thus，the corresponding optical transition energies agree well with the experimental trap depths in the SMSO∶Eu2+，Dy3+.This indicates that the neutral and negatively charged oxygen vacancies are related to the TL and LLL of the SMSO ∶Eu2+，Dy3+.Besides，the optical transition level of the Dy3+ion at the Sr site is also in a good agreement with the experimental results，confirming that Dy3+ions can be as electron trap centers in the material.It is hoped that the calculations presented in this work are applied to identify the trap centers and analyze the contribution of native defects and lanthanide ions to the TL and LLL of the long afterglow material.

2 Calculation

Geometric optimizations and electronic-structure calculations on the perfect，defective and lanthanide-doped SMSO were performed by using the hybrid DFT with the standard PBE0(Perdew-Burke-Ernzerhof-0)functional，whose exchange energy is made up of 25%exact Hartree-Fock exchange energy and 75%PBE exchange energy[14-15](as implanted in the VASP software[16-17]).Sr 4s24p65s2，Mg 3s2，Si 3s23p2，O 2s22p4and Ln 5s25p64f0-145d0-16s2(Ln＝La-Lu)electrons were treated as valence electrons，their interactions with cores were described by the projected augmented wave(PAW)method[18].Geometry optimizations were performed by using the conjugate gradient technique，and the convergence criteria for total energies and atomic forces were set to be 10-5eV and 10-1eV/nm，respectively.The one Γ point was used for the sampling of the Brillouin zone in the geometric optimizations of the supercells of the SMSO in consideration of the large cost of hybrid DFT calculations with the PBE0 functional.Formation energies(ΔEf)of the native defects(vacancies and anti-site defects)and complexes in the SMSO are calculated to study their thermodynamic stabilities.The ΔEfof the defect D in the SMSO is calculated from PBE0-calculated total energies of 1×1×2 supercells，according to the following equation[19-20]：

where D is in the charge state of q.Etot[Dq]is the total energy of the defective 1×1×2 supercell containing the Dq，and Etot[perfect]is the total energy of the perfect 1×1×2 supercell which contains 48 atoms.nirepresents the number of the atom i which is doped into(ni＞0)or extracted from(ni＜0)the perfect 1×1×2 supercell.nirepresents the chemical potential of the corresponding atoms.EFis the Fermi level and εVBMis the position of the valence band maximum(VBM).The chemical potentials of the Sr(μSr)， Mg(μMg)， Si(μSi)and Ln(μLn)are taken from the PBE0-calculated energies per atom in unit cells of the related bulk materials.The chemical potential of the O atom(μO)is derived from the thermal equilibrium conditions for reducing atmospheres(such as H2/Ar atmospheres[2])：

where μSMSOis the PBE0-calculated total energy of each formula unit of the compound SMSO.

The thermodynamic transition energy level ε(q2/q1)of the D in the SMSO(as shown in Fig.1(a))is defined as the position of the EF，where the formation energies of the D in the charge states of q1 and q2(q1＜q2)are equal[20]：

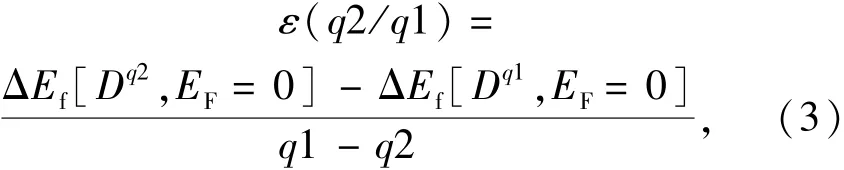
where ΔEf[Dq1， EF＝0]and ΔEf[Dq2， EF＝0]are the PBE0-calculated ΔEfof the Dq1and Dq2， respectively，when the EFis at the VBM.In the equation(3)，the adopted supercells containing the Dq1and Dq2are in their respective equilibrium configurations.The optical transition energy level εopt(q2/q1)of the D in the SMSO is defined similarly，except for that the configuration of the final state is the same as the counterpart of the initial state(as shown in Fig.1(b)).The processes of the electron exchange between the defect/dopant and the conduction band(CB)are studied according to the locations of the levels ε(q2/q1)and εopt(q2/q1)of the D in the band gap of the host.It is seen that the energy of the ZPL(Ezpl)for the above process equals to the energy difference between the CBM and the levelε(q2/q1).Similarly，the energy(Eabs)of the absorption process corresponds to the energy difference between the CBM and the levelεopt(q2/q1).

Fig.1 (a)Schematic representations for the absorption and emission processes associated with the electron exchange between the defect level of the D and the CB.(b)Configuration-coordinate descriptions for the optical transition processes“1” and “2”.

3 Results and Discussion

The SMSO crystallizes in the tetragonal system and belongs to themspace group(No.113)，as shown in Fig.2.The lattice parameters obtained from DFT geometric optimizations with the standard PBE0 hybrid functional are listed in Tab.1，along with the experimental values[21].The two sets of values are quite consistent，with relative deviations of less than 0.1%，indicating that the superiority of the PBE0 functional.There are one type of Sr，Mg and Si sites as well as three types of O(labeled as O(1)，O(2)and O(3)，respectively)sites in the SMSO.The coordination number(CN)of the Sr is eight.The averaged bond length of the Sr—O from the experiment and calculation is 0.267 3 nm and 0.266 8 nm，respectively.Both the Mg and Si are coordinated by four O.The averaged bond length of Mg—O and Si—O from the experiment is 0.189 1 nm and 0.165 5 nm，respectively， with their optimized values of 0.193 8 nm and 0.163 0 nm，respectively.The ionic radii of eight-coordinated Sr2+and four-coordinated Mg2+are 0.126 0 nm and 0.057 0 nm，respectively[22].The ionic radii of the eight-coordinatedLn3+ions(Ln＝La-Lu)are ranging from 0.116 nm to 0.097 7 nm.Besides，the ionic radius of the eight-coordinated Eu2+ion is 0.125 nm.In con-sideration of the CN and ionic radii of host cations，lanthanide ions are placed at Sr2+sites when their thermodynamic and optical transition energy levels are calculated in order to assign the origins of electron traps in the SMSO.

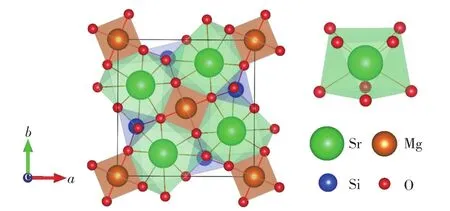
Fig.2 Schematic diagrams of the unit cell of the SMSO and the local structure around the Sr site

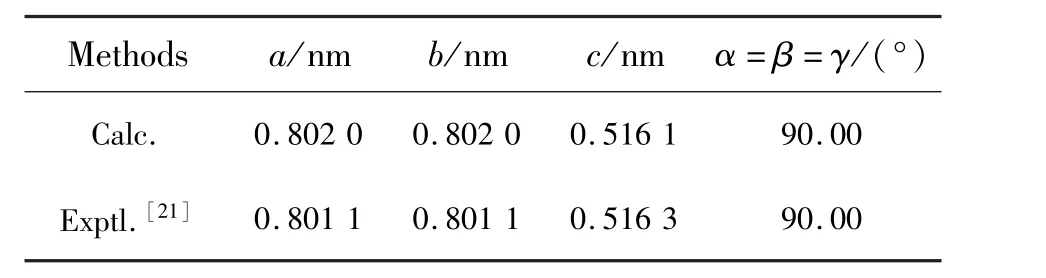
Tab.1 PBE0-optimized and experimental lattice parameters of the SMSO

The PBE0-calculated formation energies ΔEfof native defects and defect complexes in the SMSO are listed in Tab.2.The ΔEfof the vacancies at Sr， Mg and Si sites(VSr，VMgand VSi)are larger than 10.0 eV，indicating that they are not easily generated in undoped SMSO samples prepared under reducing atmospheres.One may conclude that they are not responsible to the TL and persistent luminescence of SMSO∶Eu2+，Dy3+phosphors.Three types of oxygen vacancies(VO(1)，VO(2)and VO(3))are easily generated in the host due to their small values of the ΔEf.Especially， the vacancies prefer to be at O(1)sites with the energy advantages of 31 meV and 231 meV，in comparison with O(2)and O(3)sites，respectively.It should be noted that the ΔEfof the VOin the SMSO would increase by 5.533 eV，if the O-rich condition is considered.The ΔEfof both the anti-site defects SrMgand MgSrare 1.128 eV and 2.317 eV，respectively，which means that the SrMgis much more possible in the host in comparison with the MgSr.Moreover， the ΔEfof defect complexes(VOVSr，VO-VMgand MgSr-SrMg)are also derived to study their thermodynamic stabilities.The two defects inthe complex are placed at the nearest-neighbor sites，in consideration of the mutual attraction of their opposite electrical charges of the anion vacancies(VO)and cation vacancies(VSrand VMg).It is found that the ΔEfof the complexes VO-VSrand VOVMgfor three types of the VOare relatively large，further confirming that the VSrand VMgare not easily produced in the host.The ΔEfof the SrMg-MgSris 2.569 eV，indicating that this defect complex is possibly generated in the host.This is reasonable since both the single MgSrand SrMghave the relatively low ΔEf.It should be noted that the existence of the easily generated defects in phosphors may be confirmed by various experimental measurements，such as the inductive-coupled plasma atomic-emission spectroscopy(ICP-AES)[23]and the electron paramagnetic resonance(EPR)[24].

Tab.2 PBE0-calculated formation energies ΔEfof the single defects and defect complexes(with the neutral charge states)in the SMSO

The PBE0-calculated pattern of the total and orbital DOSs for the perfect 1×1×2 supercell of the SMSO is illustrated in Fig.3.It is found that the top of the valence band(VB)is mainly composed of O-2p states，while the bottom of the CB is predominantly constituted by Sr-3d states with the mixture of O-2p states.The band gap of the SMSO calculated from the standard PBE0 hybrid functional is 7.18 eV，much larger than the calculated one(4.69 eV)[9]from the local density approximation(LDA)[25].According to Hölsä et al.[11]， the band gap of the SMSO is estimated to be 7.1 eV from the measured synchrotron radiation excitation spectrum of the Eu2+-doped SMSO，which shows a noteworthy increase of the intensity at 175 nm because of the host absorption.The PBE0-calculated value of the band gap is thus in an excellent agreement with the experimentally determined one.It confirms that hybrid DFT calculations with the standard PBE0 functional can efficiently improve the situation of the severe underestimation of the band gaps for the LDA[25]and generalized gradient approximation(GGA)[15]methods.It is noted that an accurate value of the band gap would be crucial for the calculations on the locations of thermodynamic and optical transition energy levels of the defect/dopant in the energy band of the host，further affecting the theoretical assignment of the origins of the shallow and deep electron traps of long afterglow materials.

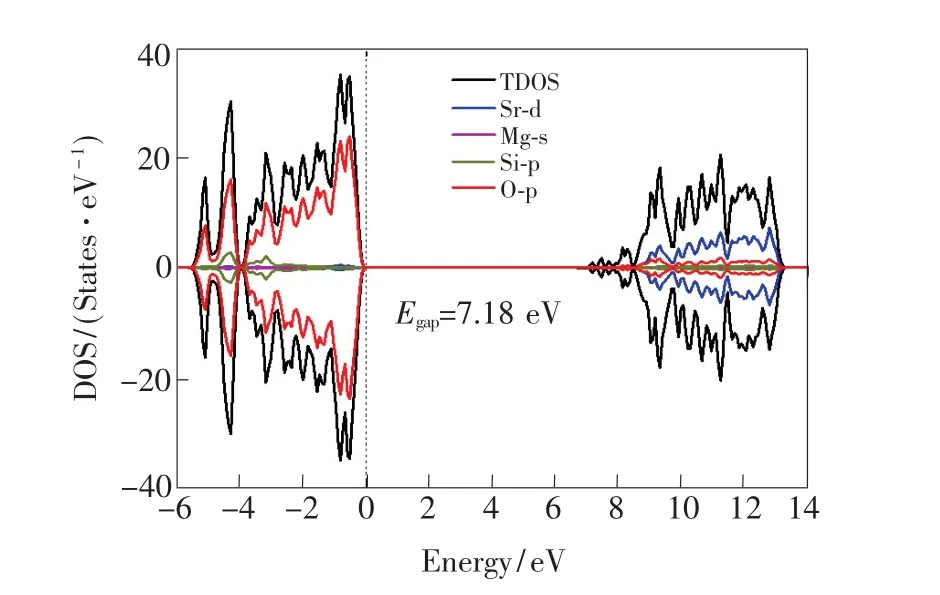
Fig.3 PBE0-calculated total and orbital-projected DOSs for the 1×1×2 supercell of the SMSO.The 4×4×3 k-point was adopted for the sampling of Brillouin zone in the calculations of the DOSs.

The PBE0-calculated defect formation energies ΔEfas a function of the EFfor the neutral and charged VO(1)， VO(2)， VO(3)， SrMg， MgSrand SrMg-MgSrare illustrated in Fig.4.The defects shown in the figure are relatively easily produced in the SMSO prepared under reducing atmospheres.The location of the EFin the band gap of the host corresponds to the synthesis conditions of samples[26]. The EFwould be in the upper and lower part of the band gap for reducing and oxidizing atmospheres，respectively.It is in the intermediate region of the band gap when a neutral atmosphere is adopted for the synthesis of samples.In general，the doubly positively charged and neutral VOin the SMSO is the most stable when the EFis in the lower and upper part of the band gap，respectively.The doubly negative charge states become the most stable for the VO，when the EFis close to the CBM.To take the VO(1)as an example，the 2+charge state is preferred when the EFis below 2.657 eV，while the neutral charge state is the most stable when the EFis in a large region of the band gap(between 2.657 and 6.606 eV above the VBM).Above 6.606 eV，the 2-charge state is the most stable for the VO(1).The figure also reveals the high similarity between the variation trends of the most stable charge states of the SrMg，MgSrand their complex SrMg-MgSrwith respect to the EF.In the most region of the band gap，their neutral charge states are the most stable in energies.This is consistent with the expectation，considering the same valent states of Sr2+and Mg2+ions.

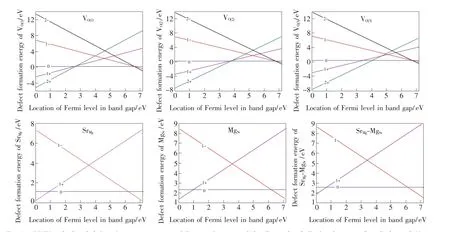
Fig.4 PBE0-calculated defect formation energies ΔEfas a function of the Fermi level EFfor the neutral and charged VO(1)，VO(2)， VO(3)， SrMg， MgSrand SrMg-MgSrin the SMSO.

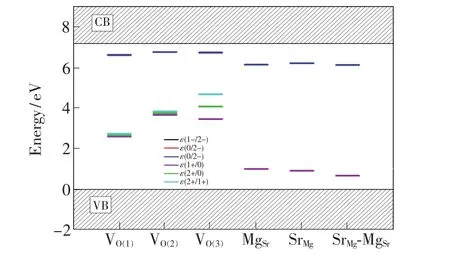
Fig.5 PBE0-calculated thermodynamic transition energy levels of the VO(1)， VO(2)， VO(3)， MgSr， SrMgand SrMg-MgSrin the SMSO.

The intersection between the two lines corresponding to the formation energies ΔEfof the defect with the charge states q1 and q2(as shown in Fig.4)gives the location of its thermodynamic transition energy level ε(q2/q1)in the band gap， which is also demonstrated in Fig.5.The charge state q2 is much more stable for the defect/dopant when the EFis below its level ε(q2/q1)， while the charge state q1 is preferred when the EFis above the level ε(q2/q1).It is found from the calculated levels ε(q2/q1)that the VOwith neutral and singly negative charge states in the SMSO may act as electron traps and be responsible to the TL and LLL.The neutral oxygen vacancies VOare supposed to be stable in the SMSO prepared under reducing atmospheres，as described above.They can capture the electrons released by Eu2+ions when the 4f→5d excitations are carried out，and consequently become negatively charged.After losing an electron(i.e.，obtaining a hole“h”)， the Eu2+ion turns into the state “Eu2++h”.The negative charge states of the VOare generally metastable except for the situation of the EFbeing extremely close to the CBM.The usual thermal activation would promote the electrons of the negatively charged VOback to the CB.These free electrons can transfer back to the “Eu2++h”， generating the 5d→4f emissions.The optical transition energies Eabsrelated to the absorption processes of the electrons from the negatively charged VO(V1-Oand V2-O)to the CBM are calculated and listed in Tab.3.The Eabscorresponding to the transformations of the charge states 1-→0，2-→0，and 2-→1-for the VO(1)，VO(2)and VO(3)are in the range from 0.587 to 0.894 eV，showing a reasonably good agreement with the trap depths determined from the TL curves by Shi et al.[5](0.67-0.73 eV)and Hai et al.[2](0.688-0.710 eV).Besides，the Eabsrelated to the negatively charged MgSr，SrMgand SrMg-MgSrare larger than 1.0 eV，possibly not contributing to the TL and LLL in the SMSO∶Eu2+，Dy3+.

Tab.3 PBE0-calculated optical transition energies of the native defects and the complex in the SMSO

The PBE0-calculated locations of the thermodynamic transition energy levelsε(1+/0)of the dopantsLn(Ln＝La-Lu)at Sr sites in the band gap of the SMSO are listed in Tab.4 and illustrated in Fig.6.The levelsε(1+/0)of theLnSrcorrespond to the transformation of trivalent and bivalent states and are conductive to analyze the valence stabilities of lanthanide ions in the host.The hybrid PBE0 calculations indicate that the variation trend of the thermodynamic transition energy levelsε(1+/0)from LaSrto EuSrshows the reasonable similarity with the counterpart from GdSrto YbSr.Among the two subseries，the Eu and Yb respectively has the lowest levelε(1+/0)， which is in the lower part of the host band gap(2.794 eV and 3.054 eV above the VBM，respectively).This is ascribed to that the 4f orbitals of Eu2+and Yb2+ions are half filled and fully filled， respectively， making their binding energies of 4f electrons much stronger in comparison with the other lanthanide ions.Eu2+rather than Eu3+ions are supposed to be stable in the SMSO prepared under reducing atmospheres，which corresponds to theEFlocated in the upper part of the band gap.Eu3+ions may be achieved in the host only if the oxidizing or air atmospheres are adopted[4].The other trivalent lanthanide ions(such as Dy3+ions[1-3])are relatively easily obtained in the SMSO under the reducing atmospheres.This may explain the coexistence of bivalent Eu and trivalent Dy ions in thematerial SMSO∶Eu，Dy prepared under reducing atmospheres.Moreover，Dy ions(at Sr sites)have the level ε(1+/0)very close to the CBM， along with their energy separation of 0.781 eV.The Eabsfor the promotion of the electron from the state “Dy3++e”back to the CBM is calculated to be 0.844 eV，showing a reasonably good agreement with the experimental values(0.67-0.73 eV[5]and 0.688-0.710 eV[2])of the trap depths for the SMSO∶Eu2+，Dy3+.To sum up，the native defects VO(with the neutral and 1-charge states)and co-doped Dy3+ions can serve as electron traps and consequently play an important role in the TL and LLL of the SMSO∶Eu2+，Dy3+， according to PBE0-calculated thermodynamic and optical transition energy levels.

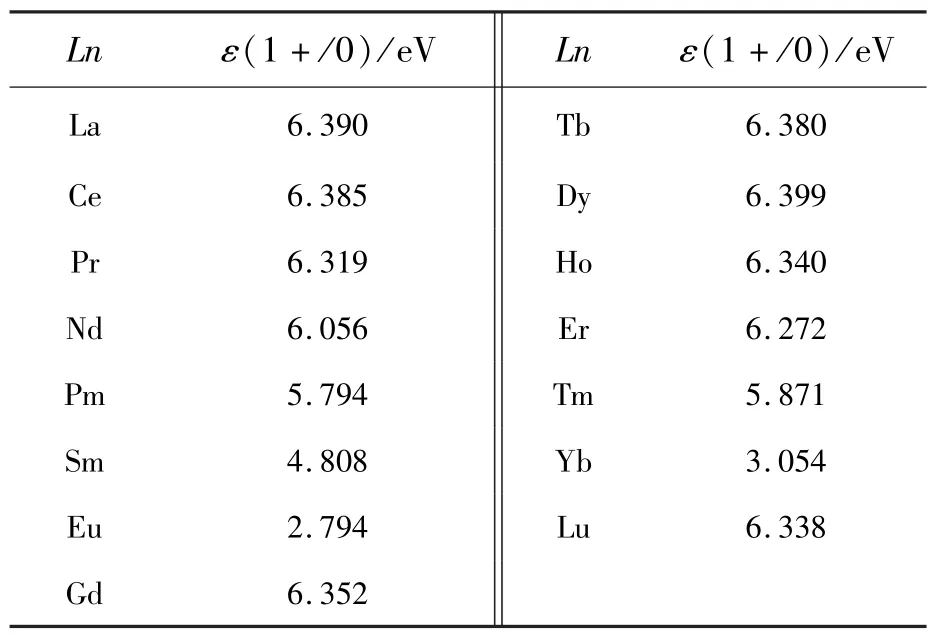
Tab.4 PBE0-calculated locations of thermodynamic transition energy levels ε(1+/0)of the dopants LnSr(Ln=La-Lu)in the band gap of the SMSO

Fig.6 PBE0-calculated thermodynamics transition energy levels ε(1+/0)of the dopants LnSr(Ln ＝ La-Lu)in the SMSO

4 Conclusion

Thermodynamic stabilities and transition levels of native defects，defect complexes and lanthanide dopants in the SMSO are calculated from the hybrid DFT with the standard PBE0 functional.The band gap of the SMSO host is calculated to be 7.18 eV，agreeing well with the experimental value(of 7.1 eV)determined from the measured synchrotron radiation excitation spectrum of the Eu2+-doped SMSO.The formation energies of cation vacancies(VSr，VMgand VSi)are larger than 10.0 eV，indicating that they are not easily generated in the SMSO prepared under reducing atmospheres.Three types of oxygen vacancies(VO(1)， VO(2)and VO(3))， anti-site defects(SrMgand MgSr)，and the complex SrMg-MgSrare relatively easily produced under reducing atmospheres.Moreover，the PBE0-calculated thermodynamic/optical transition energy levels and the corresponding energies of the relatively easily generated native defects/complexes and lanthanide dopants demonstrate that the native defect VOand co-doped Dy3+ions(at Sr sites)can act as electron traps and consequently play an important role in the processes of TL and LLL of the SMSO∶Eu2+，Dy3+.It is important to note that the neutral and negatively charged(rather than the positively charged)VOare involved in the processes of the TL and LLL according to the calculations of this work.Besides，hybrid PBE0 calculations indicate that the variation trend of the thermodynamic transition energy levels ε(1+/0)from LaSrto EuSrshows the reasonable similarity with the counterpart from GdSrto YbSr.Especially，the location of the level ε(1+/0)of the Eu is the lowest in the band gap and about 2.794 eV above the VBM.