不同湿度混凝土动力抗压性能数值模拟分析

王海龙，田 宇，银文文，孙晓燕，邹道勤

（浙江大学 建筑工程学院，浙江 杭州 310058）

混凝土结构经常在含水的环境中工作，如大坝、桥墩、地下管廊、多雨地区的混凝土路基以及铁路无渣轨道板等等。此时，自由水会通过混凝土的孔隙、微裂缝等缺陷渗入混凝土内部，内部组成的改变势必会引起其服役性能的变化。含水混凝土在其寿命周期中会遭受各种静力与动力荷载的作用，由于混凝土中自由水的存在，混凝土的静、动力力学性能会有较大的改变［1-2］。尽管目前已有一些相关的试验研究见诸报道，但是大部分研究都是集中在较大的应变率情况，地震应变率下的含水混凝土动力响应研究还相对较少。目前，学者们普遍认为在应变率小于1 s-1时，含水量对混凝土的动态力学性能有很大的影响［3-4］，但是这些工作主要是集中在试验研究，样本数量有限，还有待基于数值模拟方法开展更为深入系统的研究分析。动力荷载下混凝土的性能变化，现阶段主要可以通过惯性效应［5］和黏性效应［6-7］来进行解释。为了弄清不同湿度混凝土的动力性能变化规律，本文建立不同孔隙含水率混凝土的数值模型，将惯性效应和黏性效应同时引入分析过程，在地震应变率范围内开展含水混凝土的动力性能计算分析，从数值模拟角度深入揭示含水混凝土的动力性能变化规律与机理，并在此基础上讨论如何应用材料动力试验结果进行结构计算分析，以期为动载作用下混凝土结构设计和安全性评价提供依据。

1 数值模型的建立

1.1 混凝土骨料投放 考虑到三维数值模拟的计算复杂性，本文采用二维细观数值模型，将骨料假设为球形，对应到二维模型则为圆形。模拟时采用瓦拉文（Walaraven J C）［8］二维骨料级配曲线公式生成随机骨料模型，具体如式（1）所示，公式左侧表示混凝土二维截面内骨料粒径小于D0的概率。

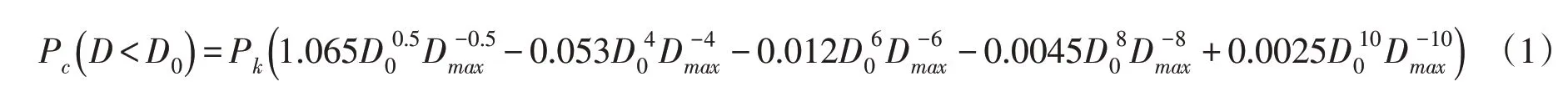
式中：Pk为粗细骨料占混凝土总体积的百分比，通常取0.75；Dmax为最大骨料粒径。

取Dmax为20 mm，Dmin为5 mm，为更精确地投放骨料，另取中间值12 mm，按式（1）分别计算出粒径为5 ～12 mm、12～20 mm的骨料比例，如表1所示。二维模型宽b取100 mm、高h取200 mm，骨料的投放结果如图1所示。

表1 二维细观模型骨料比例

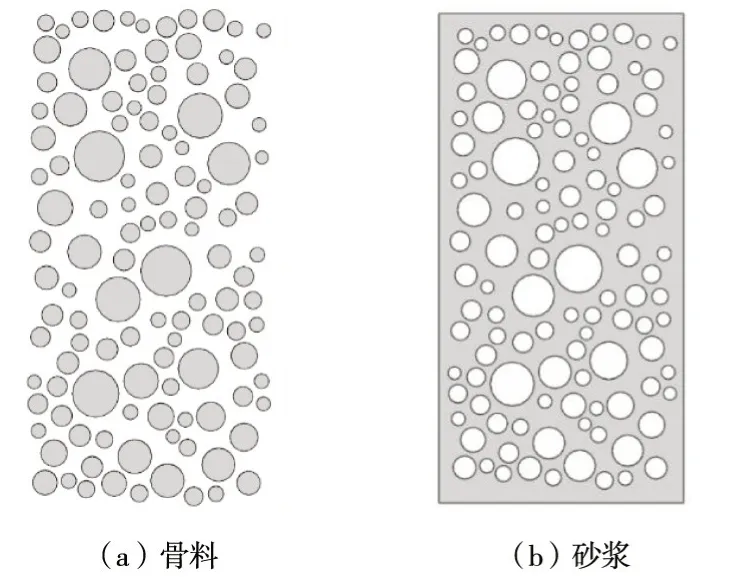
图1 骨料和砂浆几何模型

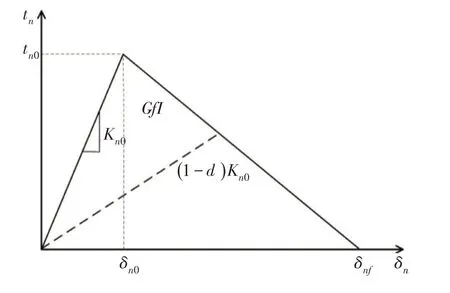
图2 cohesive单元法向应力-位移曲线

1.2 用于模拟界面与基体破坏的黏聚力单元 黏聚力单元（cohesive 单元）可以很好地模拟材料的起裂、扩展及失效全过程，因此本文采用cohesive单元来反映材料的破坏进程，其本构关系如图2所示，其中tn0为单元法向强度，δn0为对应的法向位移，δnf为单元失效位移，GfΙ为断裂能。单元的损伤起始准则由名义应力平方准则定义，不考虑单元法向压缩应力造成的损伤，软化曲线采用指数型曲线。

图3 含孔隙混凝土细观模型

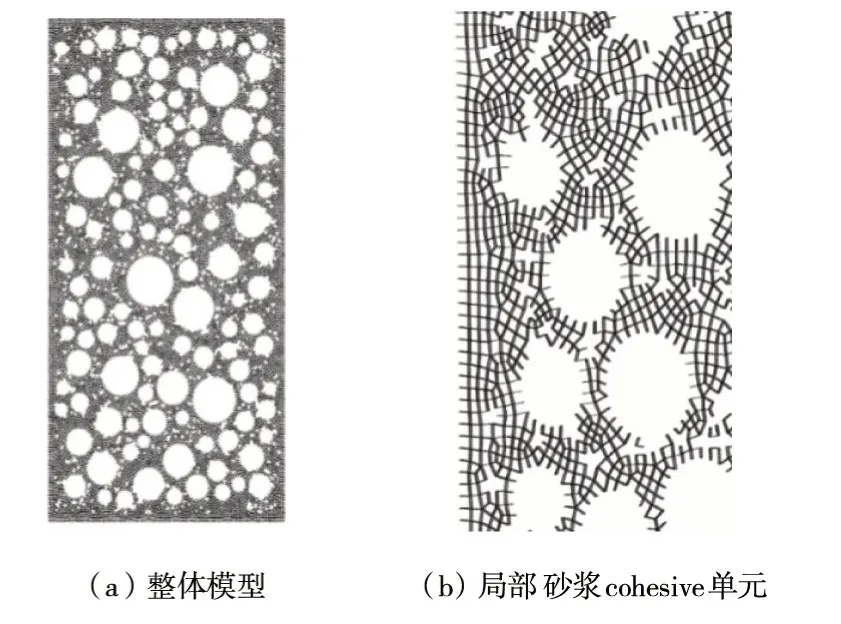
图4 砂浆cohesive单元

1.3 含水混凝土数值模型 采用ABAQUS 软件进行建模和分析。为模拟混凝土中的孔隙，通过py⁃thon编程在砂浆实体单元中随机去掉单元直至达到规定的孔隙率，模型如图3所示。通过python脚本程序处理数据文件，在骨料-砂浆界面之间和砂浆单元之间分别插入0厚度的cohesive 单元，插入砂浆的cohesive单元如图4所示。对于含水混凝土，将孔隙水视为线弹性材料填充到混凝土模型的孔隙中，孔隙水实体单元与其周边单元之间以接触的形式定义，以考虑水的流动。

混凝土饱和过程中，水分从其外表面不断浸入，直至完全饱和。假设水浸入混凝土各表面的速率相等，对于非饱和混凝土，则水分从各面浸入的距离相等。模拟得到的孔隙含水率与水分浸入距离的关系如图5所示。从图5可以看出，随着浸入时间增加，孔隙含水率的增长越来越慢，这与已有试验结果吻合［9］。分别选取水浸入各表面的距离为0（干燥）、10、20、30、40、50 mm（饱和）的含水混凝土细观模型进行受力分析，如图6 所示。认为孔隙含水率是被水分填充的孔隙面积占总孔隙面积的比值，则6 个模型对应的含水率分别为0%、26.4%、51.1%、71.9%、86.7%、100%。

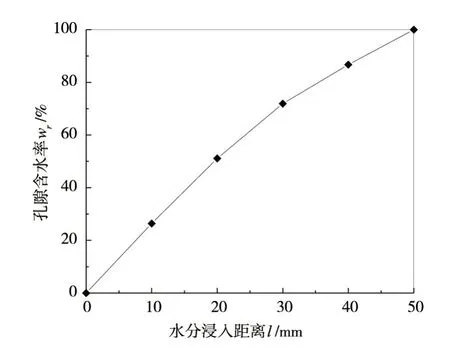
图5 孔隙含水率与水分浸入距离的关系

图6 不同孔隙含水率的混凝土模型

1.4 材料参数 认为动力荷载下混凝土宏观力学行为的变化主要是由惯性和黏性作用引起的［5］，因此采用细观模型进行动力性能模拟分析时，不改变组成材料的本构模型，即动力作用下的材料本构模型与静力本构相同。骨料实体单元采用线弹性模型，不考虑其损伤失效。砂浆实体单元采用弹性损伤模型，砂浆基体的力学行为由砂浆实体单元以及砂浆cohesive单元共同描述。界面层采用弹性损伤模型，由界面cohesive单元描述。将孔隙水考虑为弹性体，在保持其体积模量的情况下尽量降低弹性模量，以增加流动性，计算时取水的体积模量为2.2 GPa、计算弹性模量为0.132 GPa。现有研究表明［10］，水浸泡后混凝土的断裂能比干燥混凝土降低25%。考虑到相关研究较少，而混凝土中的微孔隙在数值模型中很难模拟，因此模型对含水部分的砂浆以及界面层的断裂能进行25%的折减。孔隙水cohesive单元抗拉强度和抗剪强度取0.1 MPa，断裂能取1N/m。

施士昇［11］的研究表明，混凝土的抗剪强度大于抗拉强度，为降低参数选取的复杂性，取砂浆以及界面层抗剪强度为抗拉强度的1.3倍。徐世烺等［12］建议对混凝土Ⅰ型断裂的断裂能取90 N/m，因此对界面层、砂浆Ⅰ型断裂的断裂能分别取80 N/m、100 N/m。根据Roesler等［13］的相关研究，取cohe⁃sive 单元损伤起始位移为失效位移的0.2%。砂浆和界面层的抗拉强度、弹性模量、剪切模量以及泊松比等材料参数的取值参照相关文献［14-16］，骨料和砂浆的密度分别定义为2600、2200 kg/m3。材料参数如表2所示。

1.5 动力压缩模拟 模型中cohesive 单元可以模拟混凝土动态受压时裂纹的萌生以及扩展，显示求解方法可以计算惯性效应，因此模拟中仅需对水的黏性效应合理表征即可。

1.5.1黏性效应计算方法 混凝土中的孔隙、微裂纹的尺寸及相对运动速度会影响水的黏性力，但孔隙以及微裂纹的尺寸、分布非常复杂，黏性力需要一种合适的量化分析方法。根据Rossi［6］的研究，水的黏性作用可以用Stefan效应表述：两个距离为h、半径为r的平行圆盘间充满着黏度为k的牛顿流体，当以相对速度v使二者分离时，将会产生阻止其分离的黏性力σv，即：

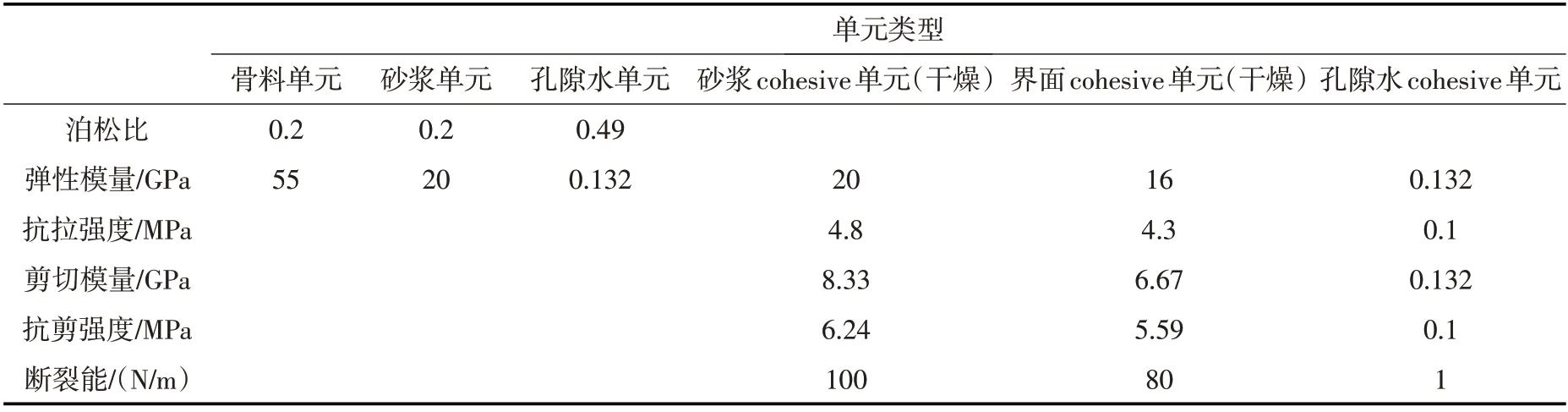
表2 混凝土细观模型材料参数

对于混凝土来说，内部存在大量的孔隙以及微裂纹等初始缺陷，当混凝土没有被特意烘干时，这些缺陷中将会有水分的存在。当混凝土受到荷载作用导致孔隙或者微裂纹发生法向相对运动或者张开时就会受到黏性力的作用，阻止裂纹扩展从而导致强度提高。

Stefan 效应解释了孔隙的法向相对运动或者裂纹的张开产生的黏性力导致的强度提高。对孔隙的切向相对运动或者裂纹滑移，当其内部有水时也会产生黏性力，这可以用牛顿内摩擦定律来描述［7，13，17］，当圆盘以相对速度v作切向运动时，液体将会产生阻止圆盘运动的黏性力τv，即：

无论是Stefan效应还是牛顿内摩擦定律产生的黏性力，均与相对速度成正比，这与动力学方程中的阻尼有类似作用，因此将水的黏性以阻尼的形式添加到动力学方程中：

对模型施加瑞利阻尼：

式中：m为质量矩阵；c为阻尼矩阵；k为刚度矩阵；F为外部荷载向量；u为位移向量。

Rossi［6］认为通过试验可以验证黏性力的影响，由于黏性力理论量化困难，因此水的质量比例阻尼系数通过试验值进行标定。由于阻尼项已经整体反应了孔隙或者微裂纹中水的黏性力的影响，因此，孔隙率并不需要特意取某值，含水孔隙只需随机分布于整个试件即可。已有的试验结果［9，18］显示，完全饱和混凝土在应变率10-3s-1时的动力强度增长因子在1.21左右。因此，以文献［9］的试验值为参考对水的阻尼系数进行标定，得到的质量比例阻尼系数为1000。

1.5.2 模型验证 使用标定的阻尼系数进行其它应变率和孔隙含水率混凝土计算分析，计算结果与试验结果的对比如图7所示，可见模拟值与试验值吻合。图中，ε̇c为加载应变率；ε̇cs为静态加载应变率；DIF为动载作用下混凝土破坏时的外荷载与静力破坏时外荷载的比值，称名义动力强度增长因子）。由于干燥试件的动力效应主要来自于惯性效应，可见本文建立的模型不仅能够较好地对惯性效应进行表征，也可以很好地反映水的黏性作用对试件动力效应的影响。

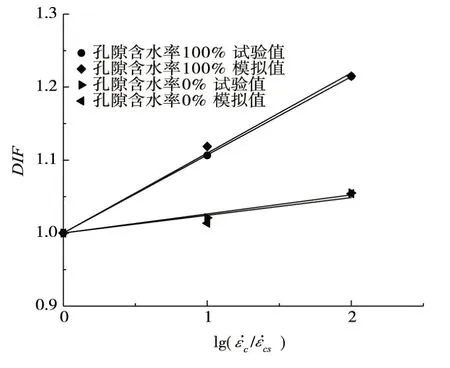
图7 数值模拟与试验动力效应对比

2 应变率的影响

2.1 应力应变曲线 以完全饱和混凝土为例，不同应变率下的应力应变计算曲线如图8所示。从图8可以看出，随着应变率增加，饱和混凝土应力应变曲线发生了明显改变，其抗压强度、弹性模量、峰值应变均增加。其它孔隙含水率混凝土亦具有同样的特征。随应变率增加，饱和混凝土应力应变曲线下降段越来越平缓，这是由于黏性作用一定程度上延缓了裂纹的快速扩展，与试验结果［9］吻合。

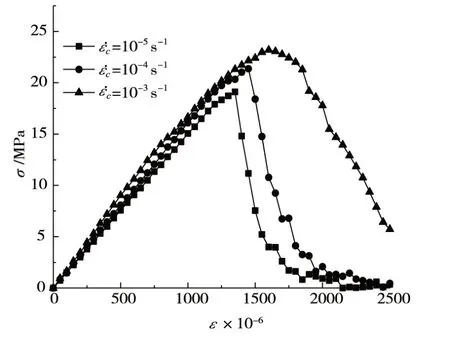
图8 不同应变率下饱和混凝土应力应变曲线

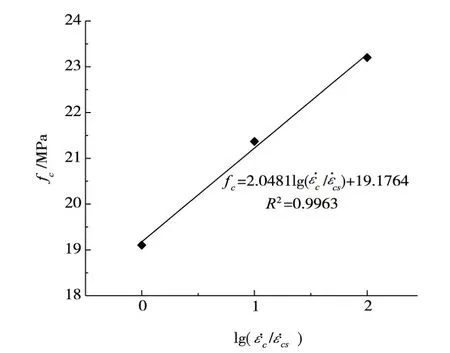
图9 饱和混凝土抗压强度与应变率的关系

2.2 抗压强度 饱和混凝土抗压强度与应变率的关系如图9 所示。从图9 可见，饱和混凝土抗压强度与应变率的对数成较好的线性关系，试验结果［9］显示的抗压强度上升梯度为1.9463，模拟结果为2.0481，吻合较好。

饱和混凝土展现出来的动力效应是模型惯性效应与黏性效应共同作用的结果。根据Griffith 理论［19］，当亚临界裂纹尺寸超过临界裂纹尺寸时，混凝土材料便会发生失效，在应变率较小时，亚临界裂纹有足够的时间去扩展，因此在应力较小时失效；在应变率较大时，亚临界裂纹没有足够的时间去扩展，因此能达到更大的应力才失效。对于数值模型，临界裂纹尺寸即为cohesive 单元的失效位移，当裂纹张开或者滑动的位移达到失效位移时，材料失效。将应变率10-5s-1时的混凝土抗压强度视为静态抗压强度，计算出不同孔隙含水率混凝土DIF 值与应变率的对应关系如图10 所示。从图10 可以看出，干燥混凝土和含水混凝土DIF 值与应变率的对数成较好的线性关系，这也与许多学者的研究结果较为吻合［18-20］。随着孔隙含水率增加，拟合直线斜率增加，即混凝土的DIF值增长越快，动力效应越强。

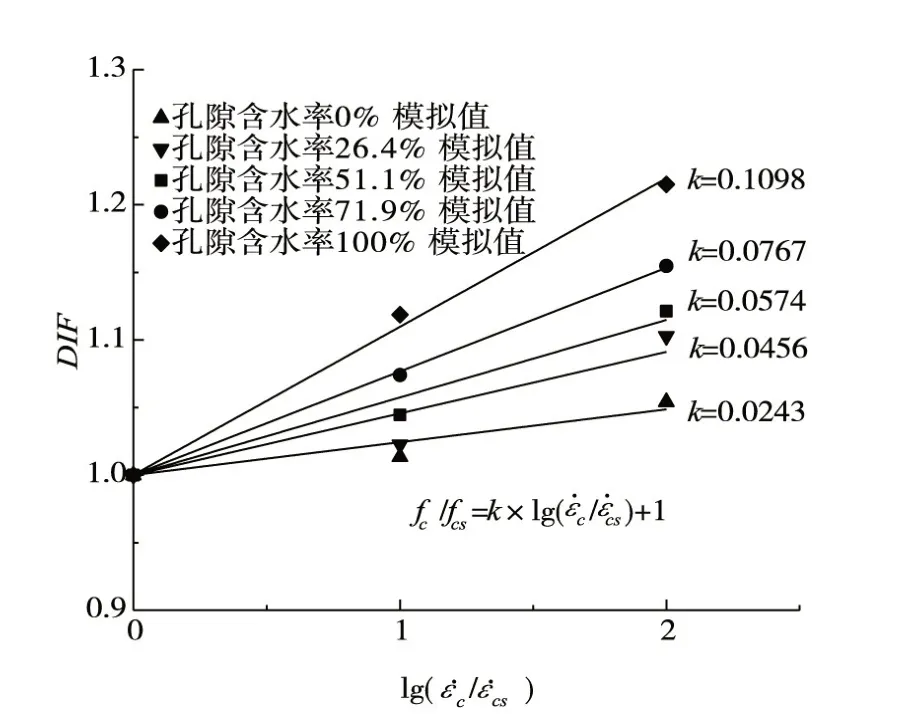
图10 不同孔隙含水率混凝土DIF与应变率的关系

2.3 弹性模量 饱和混凝土弹性模量与应变率的关系见图11，弹性模量取40%抗压强度时的割线模量，Ec为弹性模量，Ecs为应变率10-5s-1时的弹性模量。从图11可以看出，饱和混凝土弹性模量与应变率的对数有较好的线性关系，这与许多学者［18，21］的试验研究结果吻合，其它孔隙含水率混凝土也具有同样的规律，随着应变率增加，饱和混凝土弹性模量增加。这主要是因为应变率越大，黏性效应以及惯性效应越强，对原始缺陷发展的限制越强，相当于对混凝土有了一定的刚化作用从而导致弹性模量增加。

2.4 峰值应变 饱和混凝土峰值应变与应变率的关系见图12，图中，εc为峰值应变，εcs为应变率10-5s-1时的峰值应变。从图12可以看出，随着应变率增加，混凝土峰值应变增加，且二者之间有较好的线性关系。彭刚等［14］的研究发现混凝土峰值应变的数据离散性较大，但总的来说，随应变速率的提高混凝土的峰值应变呈增长趋势，其试验测得的饱水混凝土在应变率10-4s-1下的峰值应变为10-5s-1时的1.071倍，本文模拟得到的计算结果为1.074，二者较为一致。

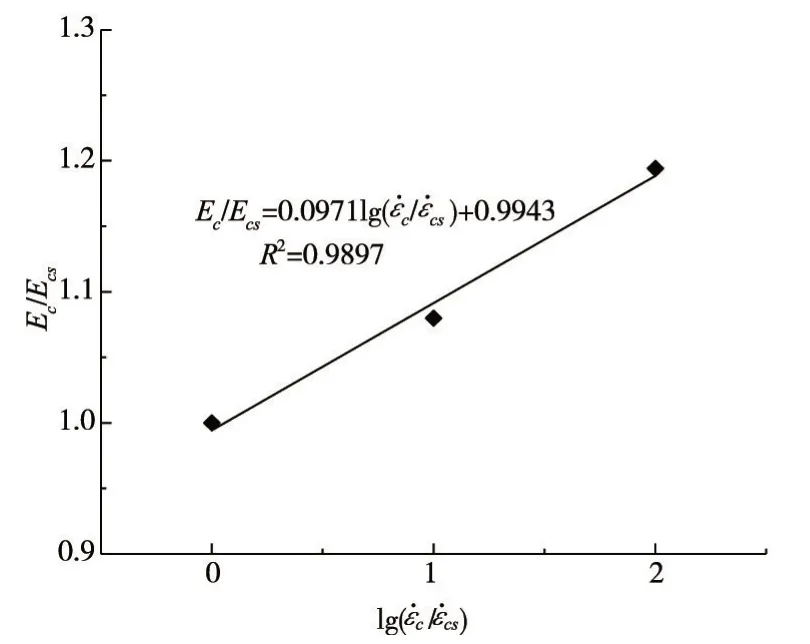
图11 饱和混凝土弹性模量与应变率的关系

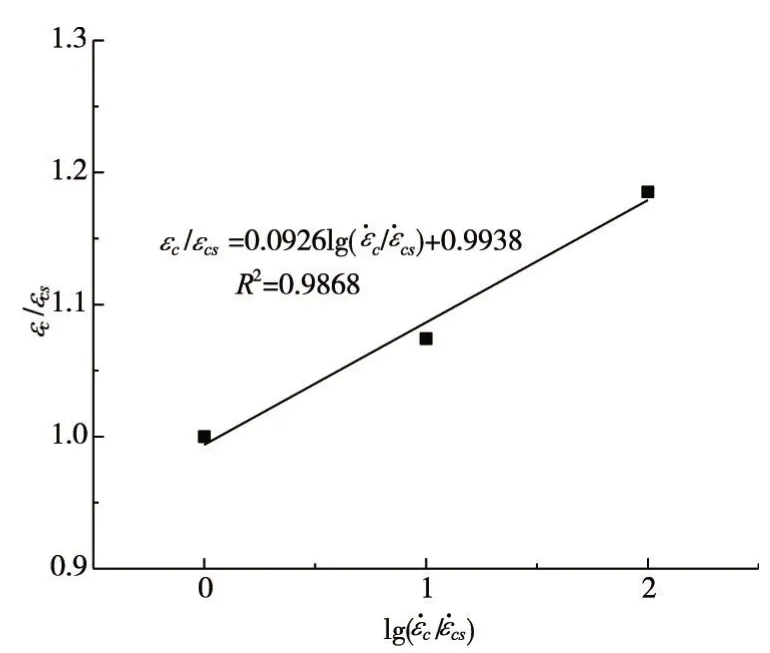
图12 饱和混凝土峰值应变与应变率的关系

3 孔隙含水率的影响

应变率为10-3s-1时混凝土动力抗压强度与含水率的关系如图13所示，从图13可以看出：动态荷载作用下混凝土抗压强度与孔隙含水率有较好的线性相关性，这也与试验结果［9］吻合。Pihlajavaara［22］用下式来描述由于水分浸入导致混凝土静态抗压强度的降低：

式中：fw为孔隙含水率为wr时混凝土的静力抗压强度；f0为孔隙含水率为0%时混凝土的静力抗压强度；c为系数。

应变率为10-5s-1的静态荷载作用下（fw/f0）2计算结果与孔隙含水率wr的关系如图14所示，二者呈现很好的线性关系。

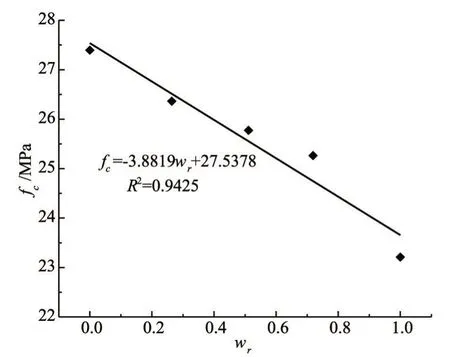
图13 应变率10-3s-1下混凝土抗压强度fc与wr关系

应变率为10-3s-1时（fw/f0）2与孔隙含水率wr的关系如图15所示，从图15可以看出，动力荷载作用下二者间亦具备较好的线性相关关系。这表明式（6）不仅适用于静态压缩，也适用于动态压缩工况，这也与试验结果［9］一致。但与应变率为10-5s-1时的结果相比，动力荷载作用下混凝土强度下降梯度减小，表明随应变率的增加，水分对混凝土抗压强度的有益作用增加，这就是水的黏性效应所致。

应变率为1×10-3s-1时混凝土动力强度增长因子DIF与孔隙含水率wr的关系见图16。从图16可以看出，混凝土动力强度增长因子与孔隙含水率成较好的线性关系，模拟结果显示的DIF 上升梯度为0.1527，这与试验结果0.16较为吻合［9］。随着孔隙含水率增加，DIF增加，即动力效应增强。根据前文可知，黏性力与裂纹相对张开或者错开速度成正比，而裂纹的张开或错开位移与远场应力成正比，即裂纹张开或错开速度与应力加载速率成正比［7，19，23］。因此，黏性力与应力加载速率成正比，试件加载速率越大，产生的黏性阻力越大，从而孔隙含水率越高的混凝土具有越大的应变率敏感性。

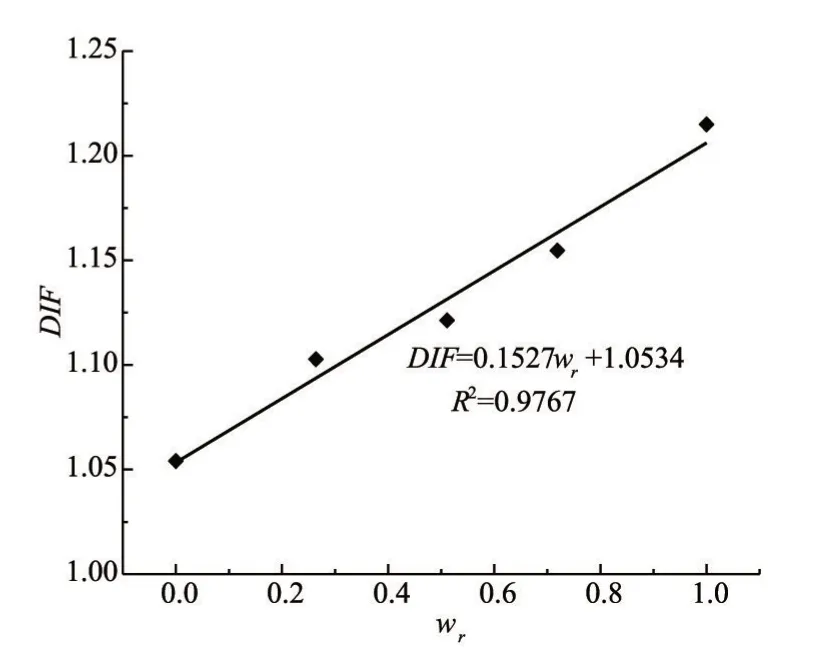
图16 混凝土动力强度增长因子DIF与wr的关系

混凝土动力分析时即使采用材料的静力参数，即细观层次上认为混凝土的组成材料为率无关材料，当考虑了惯性效应和黏性作用后，可以很好地反映动力荷载作用下混凝土名义强度随加载速率提高而增加以及混凝土名义动力强度随含水率增加而改变的现象。同样，在混凝土结构的动力数值计算中，式（4）和式（5）中已经考虑了惯性和黏性作用，在进行材料力学参数赋值时如再直接采用试验获取的动力参数，则会影响结构动力分析结果的准确性。因此，要真实反映动力荷载作用下混凝土结构的力学行为，则需考虑惯性和黏性影响来获取动力计算所需的材料参数。

4 考虑应变率和含水率的混凝土强度预测

根据前文，混凝土的应变率和孔隙含水率均会影响其动力强度增长因子和抗压强度，因此可将二者视为独立的变量，分析在二者共同作用下的混凝土抗压强度变化规律。由于（fw/f0）2与wr在静动态荷载作用下有较好的线性关系，故而采用形如下式以干燥混凝土静态抗压强度为基准对含水混凝土动力抗压强度进行拟合分析：

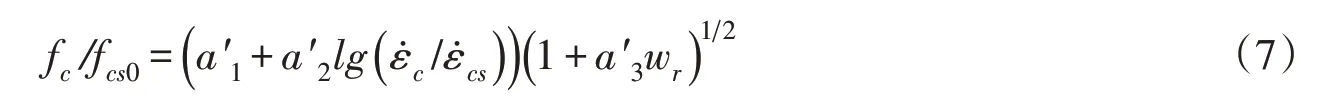
式中：fc为孔隙含水率为wr的混凝土在应变率为ε̇c时的抗压强度；fcs0为干燥混凝土在10-5s-1应变率下的静态抗压强度；a′1、a′2、a′3均为拟合值，采用MATLAB 软件进行非线性回归分析，得到a′1、a′2、a′3分别为0.9610、0.0582、-0.3364。

式（7）右侧的第一项表示应变率对干燥混凝土抗压强度的影响，第二项表示孔隙含水率的影响。模拟值与式（7）计算值的误差情况见图17，可见整体误差较小。

模型通过施加阻尼来表征水的黏性效应，水的黏性效应与混凝土孔隙和微裂纹的尺寸、相对运动速度相关。随着应变率的增加，黏性效应不断增强，也更为复杂，因此式（7）适用的范围为应变率≤1×10-2s-1，即地震应变率范围的上限。

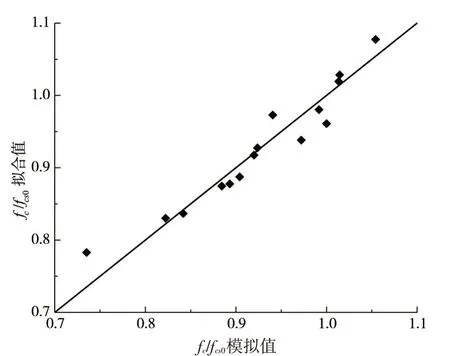
图17 fc/fcs0模拟值与拟合值的对比

5 结论

本文基于混凝土动力效应的产生机理，建立了含水混凝土动态压缩细观数值模型，分别分析了在应变率为1×10-5s-1、1×10-4s-1、1×10-3s-1工况下孔隙含水率对混凝土动态抗压力学性能的影响。得出以下结论：（1）混凝土抗压强度、动力强度增长因子随应变率增加而增加，且与应变率对数成线性关系。混凝土压缩弹性模量、峰值应变随应变率增加而增加，且与应变率对数成较好的线性关系。（2）随着孔隙含水率增加，混凝土静、动态抗压强度呈现线性减小趋势。但是，随着孔隙含水率增加，混凝土动力强度增长因子线性增加，即率效应增强。（3）混凝土动力分析时组成材料采用静力参数，当考虑惯性效应和黏性作用后，可以很好地反映动力荷载作用下混凝土名义强度随加载速率提高而增加、随含水率增加而改变的现象。（4）在混凝土结构的动力数值计算中，当动力方程中已经考虑了惯性和黏性作用，在进行材料力学参数赋值时如再直接采用试验获取的动力参数，会影响结构动力分析结果的准确性。