X射线聚焦望远镜镜片装配一体化建模和仿真

郝朝洋，邱树涵，潘文婷，李 芬，颜 远，关晓飞

（1.同济大学数学科学学院，上海200092；2.同济大学交通运输工程学院，上海200092；3.同济大学经济与管理学院，上海200092）

近20年来，随着高能天文观测的蓬勃发展，国际上先后发射了多颗X射线天文卫星。这些卫星多采用嵌套式Wolter-I型［1］或圆锥近似的类Wolter-I型［2］望远镜结构，实现了高角分辨率和大集光面积的观测，并取得了丰硕的成果。而中国在X射线天文领域的起步较晚，时间投入和资金投资相对有限，成果相对较少，目前为止仅自主研制了一颗X射线天文卫星，并在硬X射线调制望远镜（HXMT）［3］领域初步获得一些成果。此外，中国计划于2025年发射X射线时变与偏振探测卫星（XTP卫星）［4］，采用类似NuSTAR望远镜的圆锥嵌套Wolter-Ⅰ型结构［5］，并且用圆柱玻璃镜片进行压制，设计的角分辨率在1'左右，这将会是世界上首个搭载大面积X射线偏振望远镜的天文观测台，拥有超5 000 cm2的总探测面积。XTP卫星的发射将极大有利地推动极端条件下基本物理规律的研究进展。但是现今对光学元件的加工精度以及装配检测手段达不到XTP卫星的X射线聚焦能力的要求，导致X射线成像和探测技术发展困难重重。

圆锥嵌套Wolter-I型结构既相对Wolter-I型结构有着性能的提升，又没有嵌套Wolter-I型结构那样高的制作成本和难度，目前被广泛采用。考虑在装配初期进行柱面玻璃热弯效果的检查和控制，可以利用目前的计算机全息检测技术［6］，来减少每层镜片的几何误差。而影响装配质量的另一个关键因素是装配过程产生的偏差，对此则很难找到合适途径在装配过程中进行实时的检测和控制，并且实验时间长、材料成本高，人工、设施等成本高，故计算机仿真模拟是一个很好的解决手段。

目前利用有限元软件模拟望远镜镜片装配过程研究的建模方式主要为手动建模，所建模型较为简单，分析方式不够精细，不能快速、自动、精确地得到装配过程中所需的关键值以用于指导实际生产和制作。本文针对X射线聚焦望远镜镜片装配过程，采用有限元软件Abaqus结合Python语言进行二次开发一体化地建立贴近实际的装配模型，研究芯轴前后端半径、石墨条间隔角度、镜片厚度、镜片半径和装配载荷对结构面形偏差的影响，节省建模及数据处理时间，方便进行大量模拟试验并得到系列对比结果，以此指导实验室的装配实际流程。

1 镜片装配过程分析

圆锥嵌套Wolter-I型结构性能较好，又没有嵌套Wolter-I型结构那样高的制作成本和难度，是较为广泛采用的结构。它的光路结构如图1所示。图中，Lp和Lh分别为主、次轴的轴向长度，g为主次轴间的间隙，Z为光轴方向，N为第N个主镜入射X射线方向，d为相邻两个主镜光路之间的距离，θN为主镜与轴线之间的倾斜角，RN、rN分别为次镜在中心和端点到光轴的距离，其大小与主镜倾斜角相配合，使得射线经过每一层主次镜都聚焦到O点，f为焦距。

若实际主次镜面与理想锥面在入射位置和反射角度上有出入，则将出现成像误差。成像误差的具体机理如图2所示。图中，Δd为主镜面在径向上的面形误差，θ1N、θ2N分别为主、次镜面与轴线之间的倾斜角。令一束与轴平行的X射线射入，ΔL1为从主镜发生一次反射之后的轴向误差，ΔL2为再从次镜发生一次反射之后的轴向误差。本文选取的最大面型误差范围为3μm［7］。

该结构主、次镜都叠合有多层镜片，每层6片镜片，每片角度约有60°，每个玻璃镜片都撑有5根石墨条。装配时把热弯而成的柱面玻璃放在涂有超薄环氧树脂胶的石墨条上，垂直于玻璃表面对橡胶压条施加位移进行加压，在石墨条与玻璃充分接触之后，等待环氧树脂胶凝固，最后按一定次序卸载压条。表1为镜片装配时其中一组常用的几何参数。

把柱面的玻璃压制到圆锥面的安装面上，玻璃会变形产生偏差。会影响到玻璃镜片安装的面形偏差因素有：玻璃自身热弯质量、玻璃半径（假设芯轴尺寸已固定）和装配工艺等。本文默认玻璃质量达标，仅考虑玻璃半径和装配工艺等的影响。由于要进行大量的实验对比分析，通过有限元软件多次手工建模的成本很高，本文将通过有限元软件Abaqus结合Python语言进行二次开发，建立一体化建模流程，在此基础上进行仿真实验，并尝试为装配优化工艺提供技术支持和建议。

2 一体化建模和仿真流程

2.1 模型设置

不同于贺鹏飞等［7］的相关研究，本文采用三维模型进行仿真和分析，考虑到芯轴刚度较高，在建模中不考虑其形变，并将石墨条与芯轴的接触面简化为固定约束。考虑到6个镜片在结构上具有对称性，但单个镜片在装配过程中并不具有对称性，本文将模型简化为研究一个镜片。如图3所示，1号压条为中间压条，2、3号压条为二级压条，4、5号压条为三级压条，压条对应的石墨命名顺序也相同，这里压条加载顺序为1—2—3—4—5。

图3 三维黏接分析有限元模型Fig.3 3-D finite element model

建模和仿真采用Abaqus有限元分析软件，为避免剪切闭锁问题使用C3D8R单元，也可使用C3D8或C3D8I单元。局部有限元网格演示见图3，各材料的性能参数见表2。

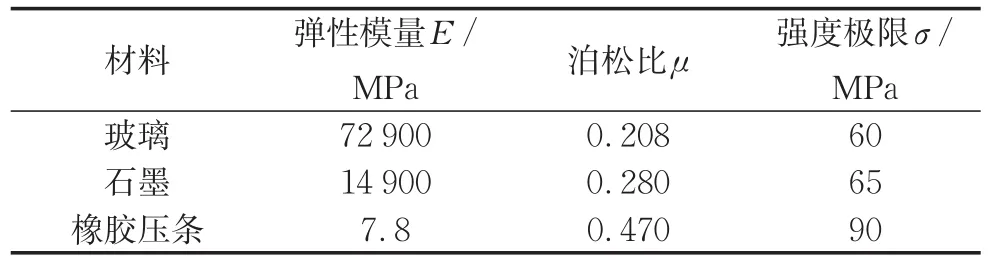
表2 主要材料参数Tab.2 Parameters of materials

2.2 荷载加载和边界条件

本文研究不同半径镜面的加载黏合过程，其与芯轴前后端的半径有以下3种关系：镜面半径大于芯轴前后端半径、镜面半径小于芯轴前后端半径和镜面半径介于芯轴前后端半径之间。这3种情况下力荷载的作用有所不同，第一种情况下中间压条1上的力荷载是为了使镜片接触石墨1（自然状态下分离），之后在2～5号压条上施加的力荷载与压条1的作用相同，这时压条1所需的力荷载会略小；对于第二种情况，压条1开始不需要荷载（自然状态下镜片接触石墨1），随着2～5压条上荷载的施加，压条1需要一定荷载来防止镜片与石墨分离；情况三则是前端为第一种情况，后端为第二种情况。对于不同参数下所需荷载的最优数值，以前的研究均采用的是反复试算的方法，这无疑会大大增加工作量，并且实验结果的精确性不够高。

本文将建立自适应的位移荷载求反力法减少计算量并提高计算精度。位移荷载求反力法的目的是使镜片与石墨条接触，使用位移荷载配合自由度约束可以取代力荷载。首先在建模过程中旋转镜面与压条，使得镜面中线、1号压条与1号石墨条平行，再将2～5号压条绕芯轴旋转到1号压条两侧，最后抬升镜面与压条使它们与石墨条分离；接着依次为1～5号压条施加位移荷载，位移大小用几何方法计算，并在每步对镜面、压条和石墨条施加相应的自由度约束。同时设置场输出和历程输出时对压条选择反作用力（RF），这样仿真结束后可以逐帧提取反作用力，其结果即为所需荷载，并可提取节点坐标计算面形误差。位移荷载求反力法有其局限性，仿真实验中发现多数情况下（实际实验也证明）并非在刚好接触的状态下其面形偏差最小，而是在接触的基础上增加一点荷载（合力或均布压强）可以使得面形偏差更小，于是对算法进一步改进建立自适应的位移荷载求反力法。

自适应的位移荷载求反力法的算法分为两步：第一步为搜索阶段——首先新设4个荷载参数，分别为1号压条荷载、2、3号压条荷载，4、5号压条荷载（利用对称性）和步长，接着对荷载参数在一定范围内进行遍历（此时选取的搜索步长是关键），按照之前的几何参数进行几何建模，施加位移，接触后施加荷载，并取消位移约束，如果满足接触且计算得到的面形误差小于位移荷载法计算得到的面形误差，则记录当前参数；第二步为优化阶段——在搜索阶段已经获得了较优参数的大致值，接着再缩小步长，对参数附近的值进行遍历，直到满足需要。

以上面形误差的计算根据镜面几何参数计算标准锥面方程，提取有限单元节点的三维坐标（x，y，z），根据y和锥面方程计算标准半径R，再用计算径向误差（见图1和图2）。本文取所有节点最大误差的绝对值作为整个镜片的面形误差。

2.3 Abaqus-GUI一体化开发

基于模型设置和载荷加载方法利用Python对Abaqus进行二次开发。Abaqus脚本接口可以基于Python语言的定制开发。这个接口与图形界面无关，可与内核直接通信，可以执行重复性计算、创建模型、做优化分析、访问输出数据库、创建Abaqus的插件等。使用Python对Abaqus进行二次开发的好处有：语言简洁，易于理解，简化手动繁琐的操作；自动化，如进行后处理可以自己编写专门的模块；能够实现参数化分析；可编写独立模块，具有独立性和可移植性；具有优秀的异常处理机制［8］。

Abaqus脚本与Abaqus的计算机辅助计算（CAE）模块的通信关系如图4所示。这里Python解释器有3种输入接口分别为GUI，命令行接口（CLI）和脚本，并保存为rpy文件。经过有限元分析计算以后结果保存并输出数据库中（ODB文件），其由模型数据和结果数据组成。输出数据库ODB文件的层次结构见图5。

图4 Abaqus脚本与Abaqus/CAE的关系Fig.4 Abaqus script versus Abaqus/CAE

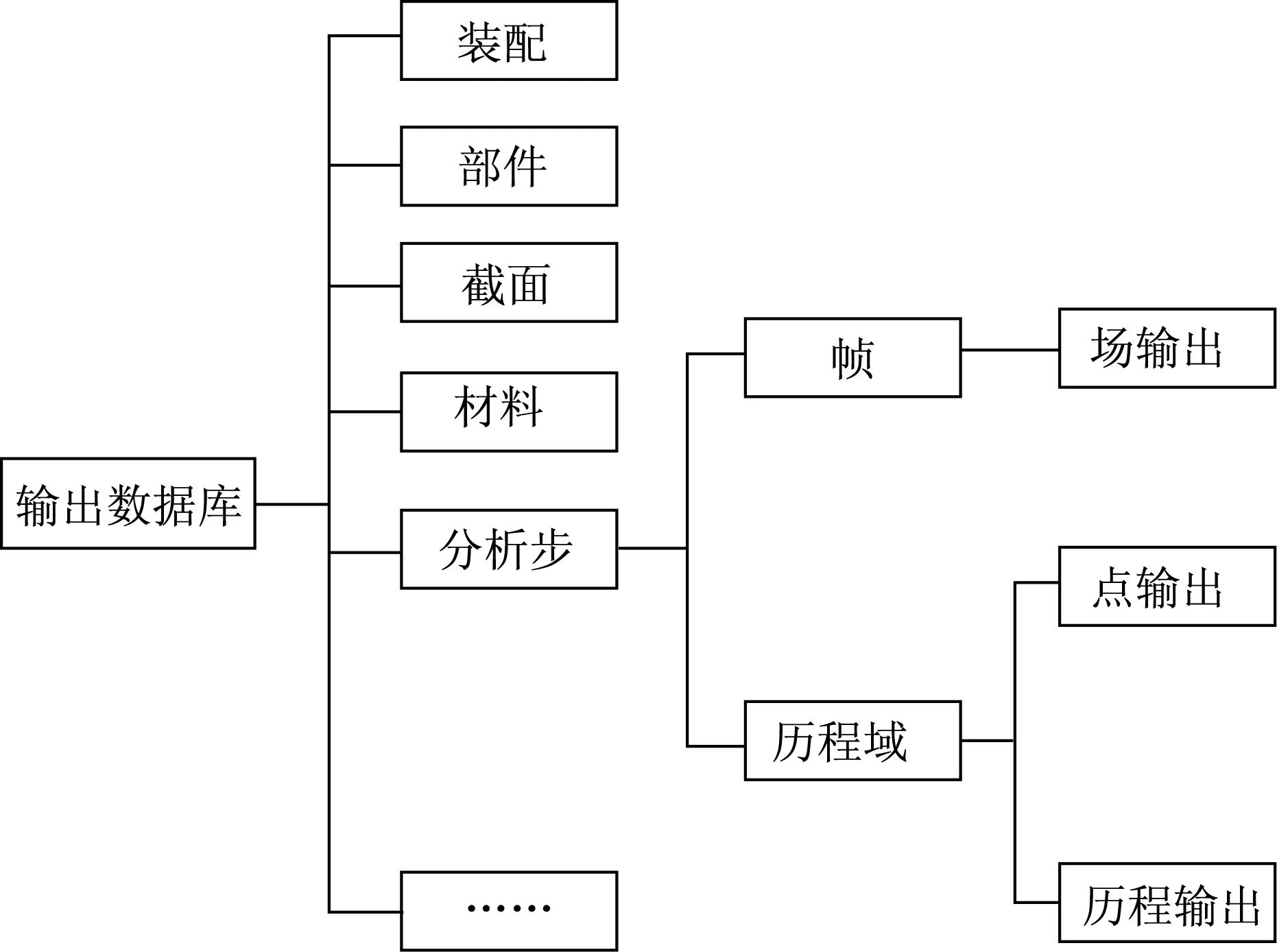
图5 输出数据库ODB的层级结构Fig.5 Hierarchy of the output database ODB

自适应建模分析算法利用Python编写脚本实现，仿真生成ODB输出数据库文件后，则用Python脚本对仿真过程和结果中的关键数据进行提取，然后用数据分析工具（如Python、Matlab）进行分析。此外，对于传统的手动建模过程中需要反复切换模块、点击按钮、输入数据等，而且难以撤销，若使用纯代码进行建模，则每次都要修改部分代码，并且用户体验不佳，操作比较复杂。本文同时设计了GUI界面进行仿真分析，有效地提高前后处理效率，节省建模及数据处理时间，利于用户操作且还可以规避一些人为的错误。

界面的设计如图6所示，有常规计算和确定最佳荷载组合计算两种窗口。在常规计算窗口中，有几何参数栏（前后端半径、镜筒高、石墨条厚度与旋转角度、镜面半径与厚度、压条厚度等）、材料参数栏、仿真参数栏（石墨条、镜面、压条网格大小）以及位移荷载求反力法和自定义荷载两种模式，勾选自定义荷载后可输入想要的压条荷载；在确定最佳荷载组合计算窗口中，有几何参数栏、仿真参数栏以及自定义搜索区间和在求反力法结果附近搜索两种模式，勾选求反力法结果附近搜索后将先进行求反力法计算再搜索包含改计算结果的区间，此外加入参数输入约束如各数值为正数、前端半径需大于后端半径等。计算的过程输出将放在Abaqus安装路径下的Temp文件夹中。

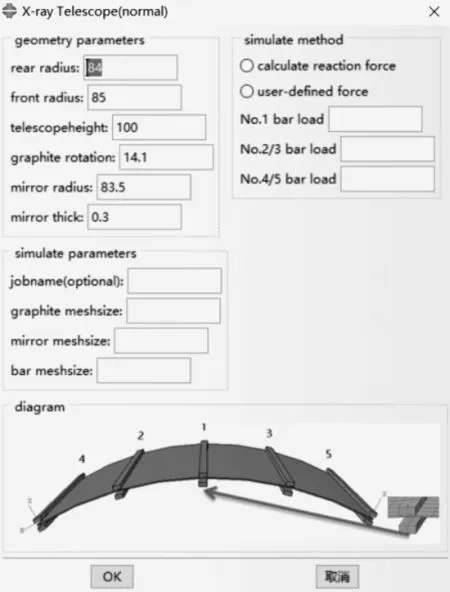
图6 GUI界面Fig.6 GUI interface

2.4 收敛性及精度的影响因素

在仿真过程中，有限元分析比较困难的是计算达到收敛，大多数情况下不收敛的原因难以找到，需要进行大量的试算。不收敛原因主要有：①网格划分不合理。如网格划分过粗或者接触时主从面的网格粗细没有掌握好，有时候主面和从面的网格大小为倍数关系会造成穿透现象而不准确且无法收敛。点对面离散时，若从面网格比主面网格细，则不会发生穿透，从面和主面都发生了正常的变形；若从面网格比主面网格粗，则会出现穿透。面对面离散时，情况类似。②针对接触分析问题。可以设置微小的过盈量，以保证在分析一开始就已经建立起接触关系。另外不能在接触面上使用C3D20、C3D20和C3D10等单元类型，避免过约束。此外，对本问题使用减缩积分单元收敛效果会比完全积分单元和非协调单元要好。③分析步设置不合理，两个复杂步骤应该放在不同的分析步里，分析步的初始步长、最小步长、步长缩减系数、最大尝试次数都关系到能否收敛。在接触分析步中，位移主要有两个阶段，一个是镜面的两边还没有接触到最外侧的石墨条，这时的运算很简单，分析步长也很大，但一旦镜面的两边接触到了最外侧的石墨条，也就是进入了第二阶段，这时候运算开始变得复杂，分析步步长将急剧减小，若减小的尝试次数超过5，则Abaqus会以为算不出来而报错，这时候需要在分析步编辑器和通用求解控制编辑器中调整初始步长、最小步长和最大尝试次数。④边界条件约束不当，缺乏约束会产生数值奇异或零主元。⑤使用不恰当的位移荷载，由于精度问题，位移荷载可能会造成较大的局部应力，产生不合理的形变，使得准确度较低、收敛很困难。⑥使用不恰当的力荷载，如静力分析模块中在没有其他约束的时候对物体施加纯力，会导致分析步长越来越小直至不能收敛。

针对计算的精度，考虑到Abaqus软件默认精度及计算机存储精度的限制，可以利用Abaqus仿真计算的无单位性，对仿真参数进行放大或缩小以提高计算结果的有效数字，使得仿真计算能最大程度保留有效数字，提高计算精度。此外，还需要对X射线聚焦望远镜镜面压弯有关材料的弹性形变特性与塑性形变特性、镜面与环氧树脂、石墨间隔条的接触摩擦进行细节上的处理，另外也可使用Fortran语言用户子程序的开发，以上改进会使得数值仿真结果更为准确。

3 仿真结果分析

根据上述一体化建模和仿真流程，本文将依次研究前后端半径、镜片半径、石墨条间隔角度等对装配结果的影响，并对数据进行进一步的分析。下文中所有演示图默认为前端在下，1号石墨条指向1号压条为x轴正向，镜片轴线向上为y轴正向，4号石墨条指向5号石墨条为z轴正向（图3）。

3.1 前后端半径、镜片半径对装配结果的影响

根据镜片半径与芯轴前后端半径的3种大小关系，本文用多组数据进行实验，得出这3种关系应力分布、面型残余的分布等基本特征。这里芯轴参数见表1和表2，镜片内表面半径见表3，镜面厚度为0.2 mm，镜筒高为100.0 mm，石墨条之间间隔角度为14.1°，石墨条与压条厚度为1.0 mm，石墨条、镜片、压条网格大小分别为2、3、6 mm，计算结果见表3（仅展示其中3组）。

不同尺寸镜面应力分布、面形误差分布见图7到图9。总体来看，压条附近区域面形误差都较小，这是因为压条本身与石墨条的贴近对镜面的约束强度较大，而其他区域则缺乏直接约束；而压条附近区域镜面应力都比较大，但计算而得的最大应力均低于玻璃的强度极限。对于前两种情况的镜片，前端应力普遍大于后端，而第三种情况前端与后端应力分布较为均匀。从应力的最大值看，最大应力与最大误差随镜片内表面半径增加而减少。第一种情况下径向实际值往往偏大，而第二种情况则偏小，第三种情况则较为对称。

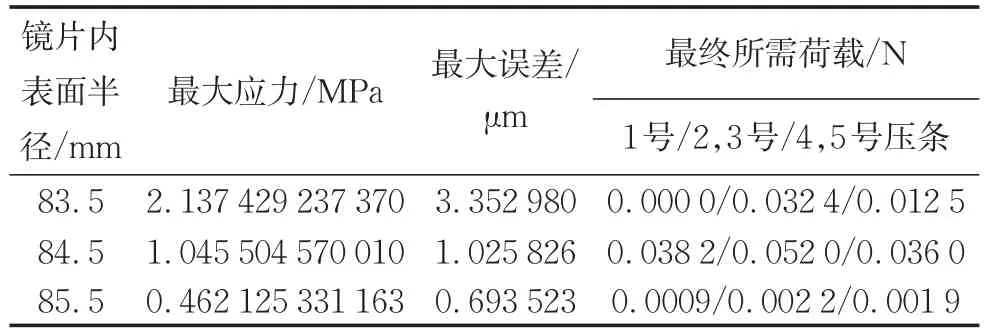
表3 基于三种镜片内表面半径的计算结果Tab.3 Computational results based on three inner surface radius of mirror

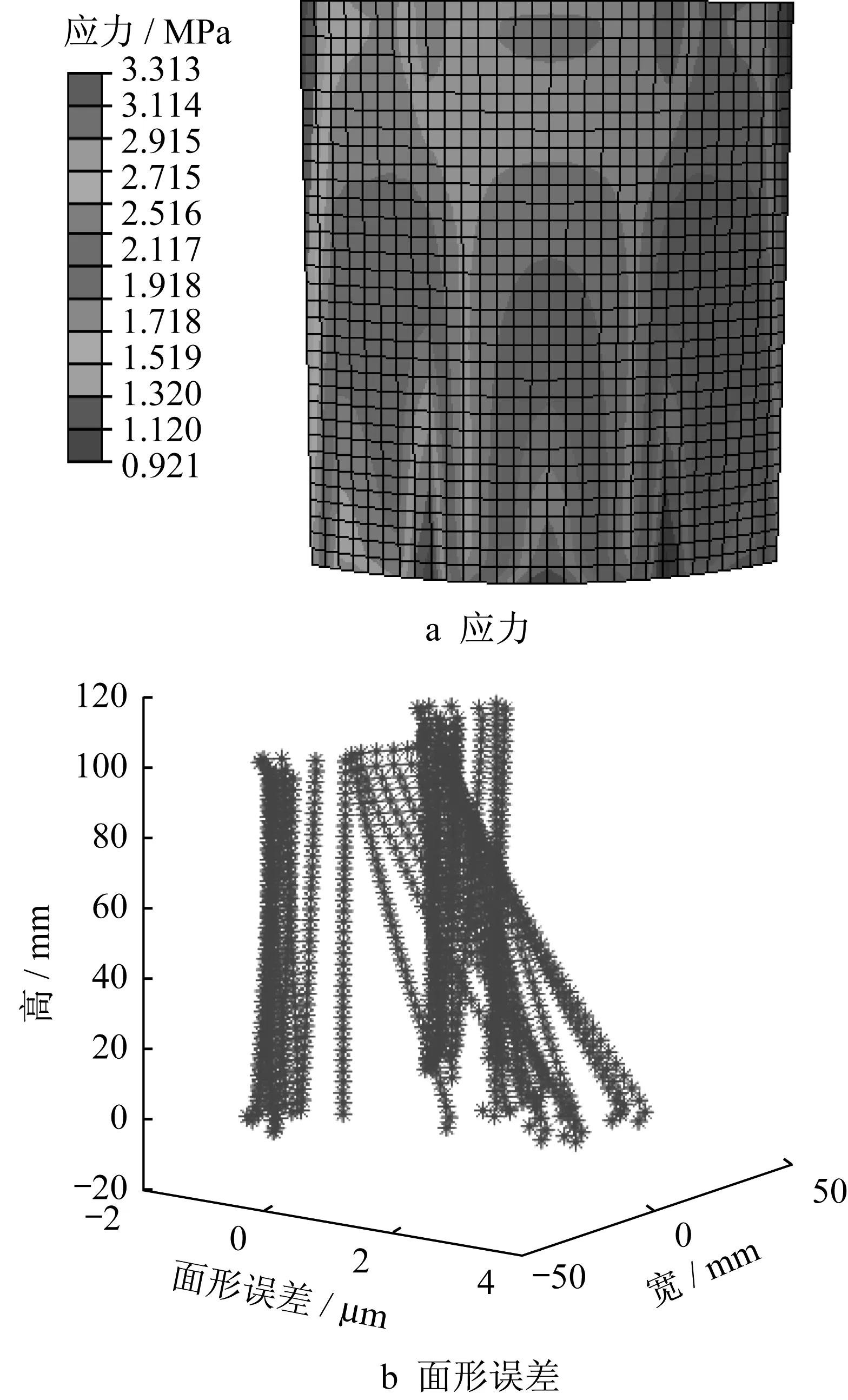
图7 镜面内表面半径为83.5 mm时的应力和面形误差分布Fig.7 Distribution of stress and surface error when inner surface radius of mirror is 83.5 mm

注意到虽然在最大误差上三维模型与二维模型类似，但面形误差分布上两者还是有所不同。尤其是当镜片半径介于前后端半径之间时，其分布情况较为特殊，且综合来看镜片半径略大于前后端半径的时候，最大应力与最大误差以及误差分布的情况都较好，而过大的镜面半径也会造成较大误差。

从所需荷载的角度看，可以观察到当镜片内表面半径小于前后端半径时，压条1最终所需荷载几乎为0；介于两者之间时，所需的荷载较大（要把其中一端压紧）；大于两者时，需要一点力来抵消其他4根压条的影响，与预想的结果相符。

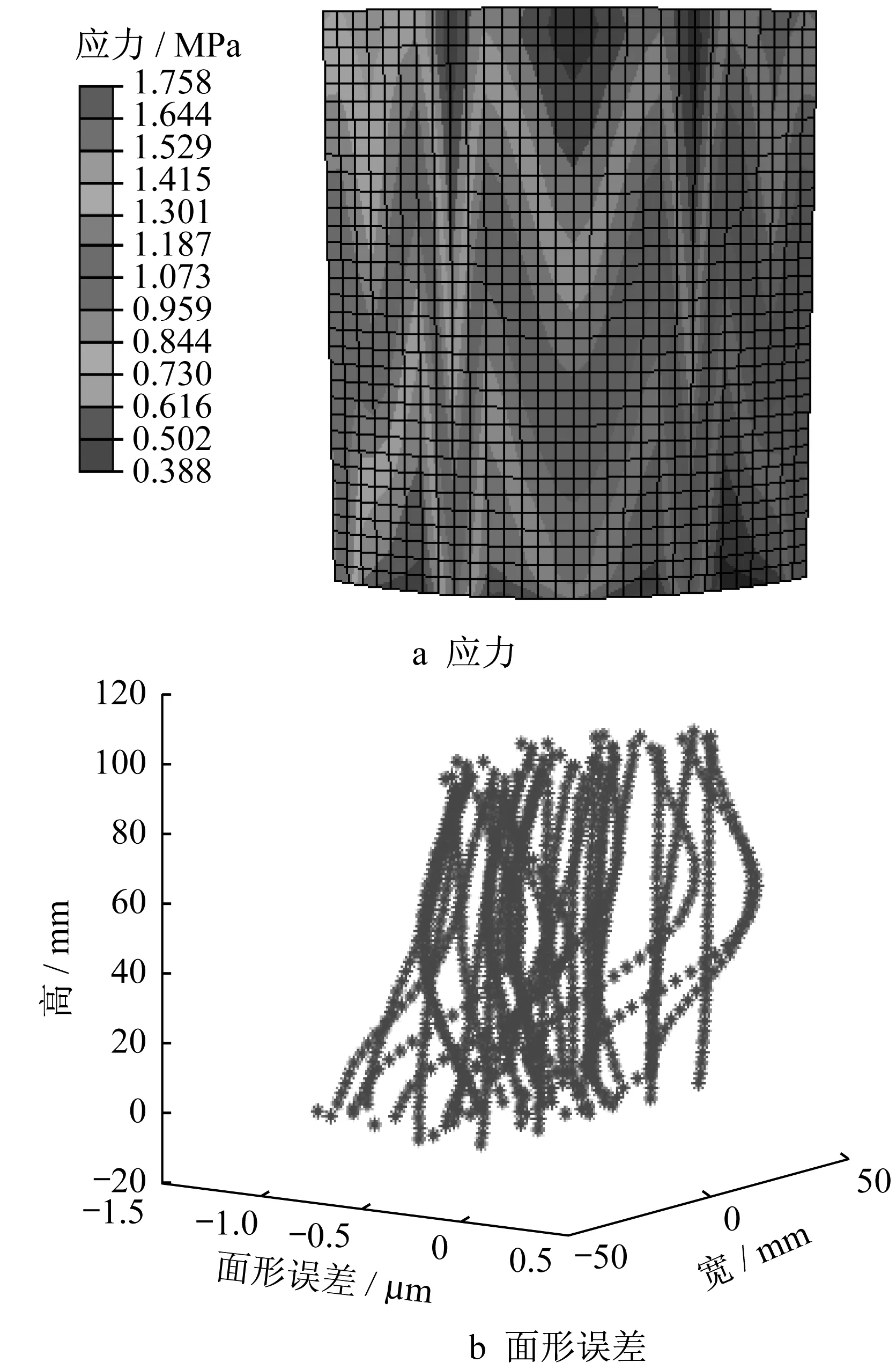
图8 镜面内表面半径为84.5 mm时的应力和面形误差分布Fig.8 Distribution of stress and surface error when inner surface radius of mirror is 84.5 mm

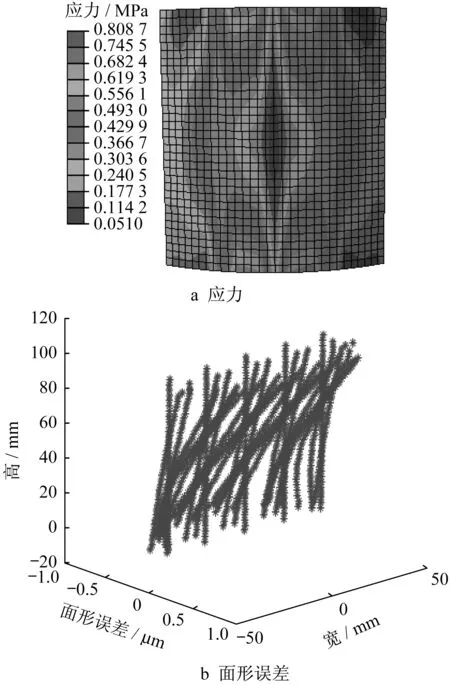
图9 镜面内表面半径为85.5 mm时的应力和面形误差分布Fig.9 Distribution of stress and surface error when inner surface radius of mirror is 85.5 mm

3.2 镜片厚度对装配结果的影响

当前的镜片厚度主要有0.2、0.3、0.4 mm 3种，由上一小节知，镜片半径略大于前后端半径时效果较好，故本小节所使用的镜片半径为85.5 mm，其余参数相同，以此分别分析 0.20、0.25、0.30、0.35、0.40、0.45、0.50 mm这7种规格镜片厚度对装配结果的影响，计算结果如表4所示。图10展示其中一种情况下整体应力和面形误差分布。

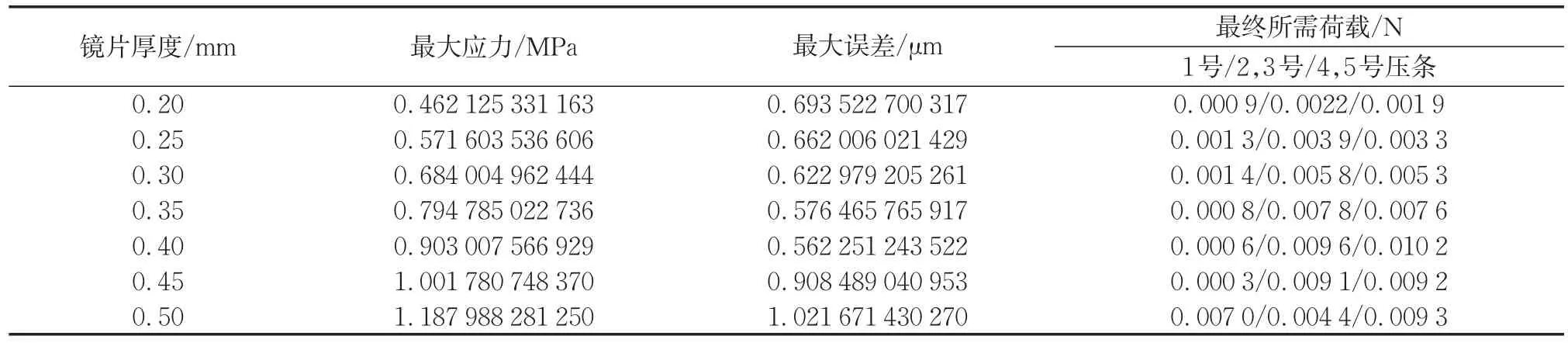
表4 7种镜片厚度下计算结果Tab.4 Computational results of 7 different thicknesses of mirror

由图11可知，镜片厚度改变，应力与面形误差分布规律相同。可以发现，随着镜面厚度的增加，最大应力增加（但仍远低于玻璃的强度极限），所需荷载无规律变化，而最大面形误差减少，因为根据材料力学，厚度大的板壳结构不容易发生较大的形变；但当镜面厚度增加到一定程度后，应力增加较快，使得镜面出现更大的形变，最大面形误差会突增到比原来还大。经过多组数据分析后镜片厚度在0.3～0.4 mm之间为佳，厚度过大或过小均会使面形误差增加。

3.3 石墨条间隔角度对装配结果的影响

由上一小节知镜面厚度为0.4 mm时面型最大误差小，故本小节所使用的镜片厚度为0.4 mm，其余参数与上一小节相同，以此分析石墨条间隔角度对装配结果的影响。表5给出了石墨条间隔角度不同时的计算结果。石墨条间隔角度改变，应力与面形误差分布规律相同，此处不再赘述。可以发现，随着石墨条间隔角度的增加，最大应力先减后增，而最大误差的改变则没有明显规律（总体上先减后增），故石墨条最佳间隔角度只能通过自适应算法求得。需要注意的是，石墨条间隔角度的影响要综合考虑每一层镜片的情况，要找到对每一层镜片来说最大面形误差最小的石墨条最佳间隔角度，而不能只针对某一层最小。这些都体现出了一体化建模和仿真的优势。

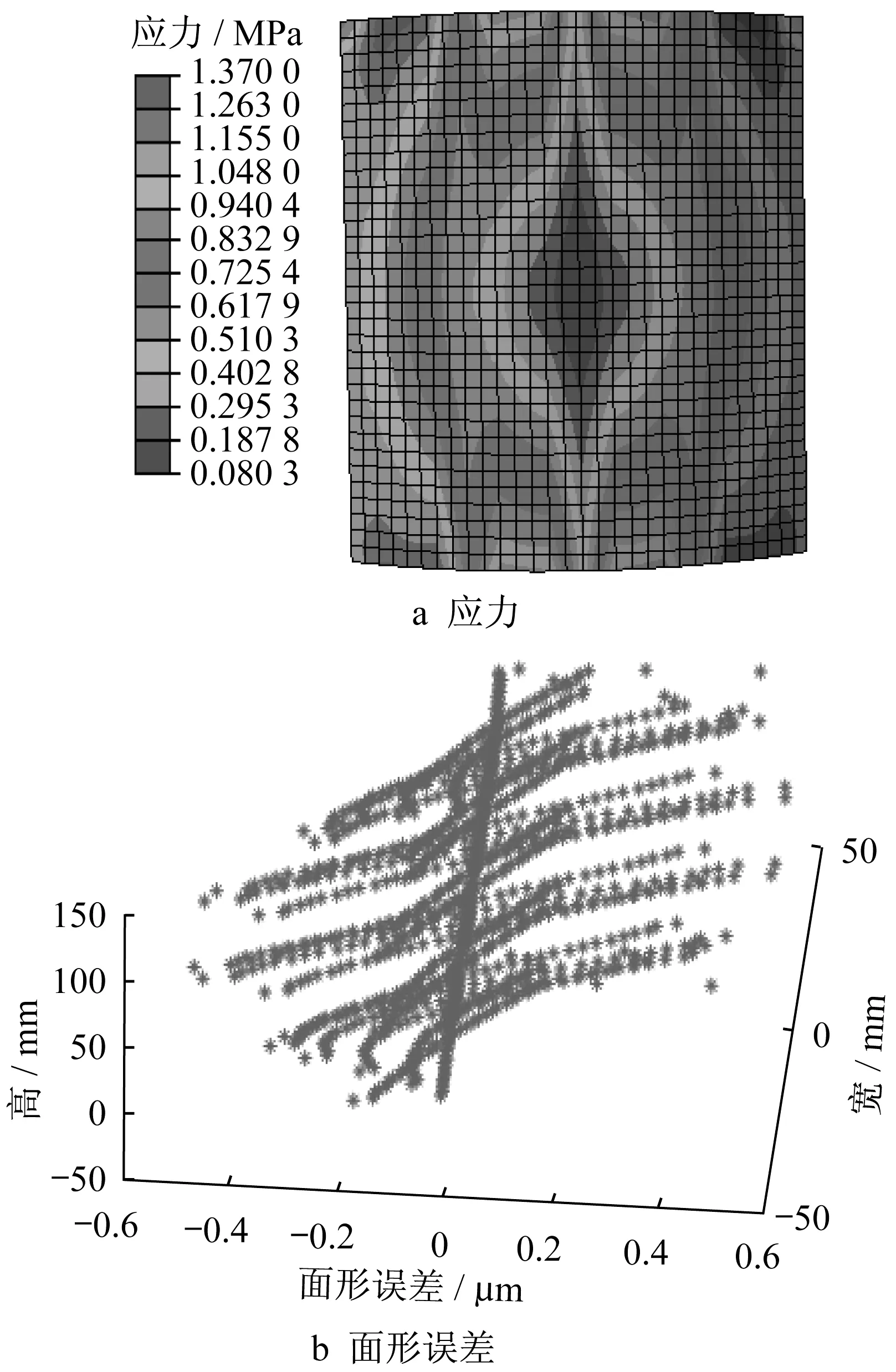
图10 镜片厚度为0.35 mm时的应力和面形误差分布Fig.10 Distribution of stress and surface error when thickness of mirror is 0.35 mm

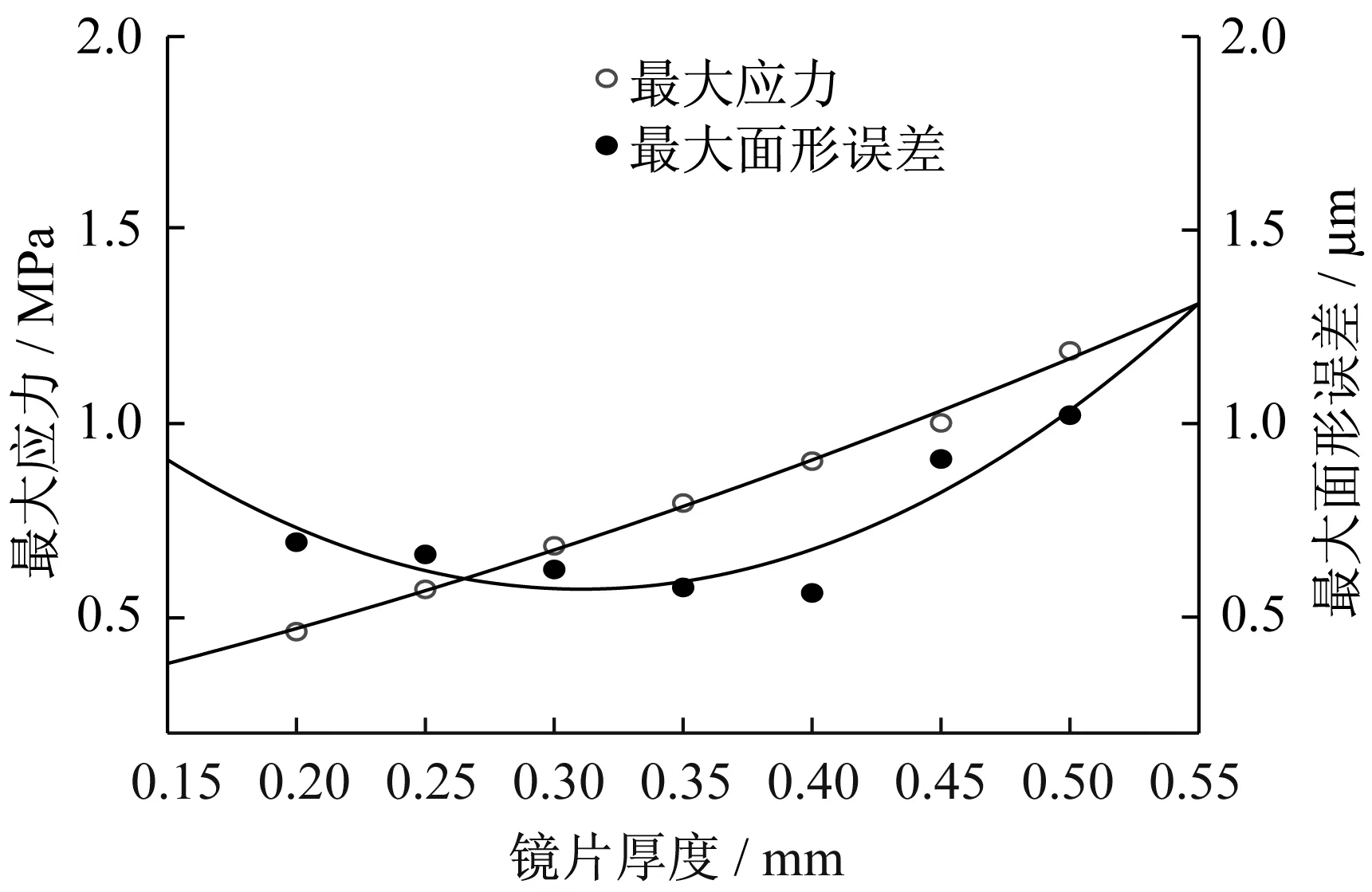
图11 镜片厚度与最大应力、最大面形误差的近似关系Fig.11Mirror thickness versus maximum stress and surface error

3.4 最佳荷载组合研究

本文利用自适应算法在一定区间内对各镜片半径下的最佳荷载组合进行探究，装配相关参数与镜片厚度为0.3 mm的算例相同，得到结果见表6。从计算结果可看出，最佳荷载组合与施加位移求反力的结果是相近的，且由于所需荷载的数值较小，算法的遍历搜索步骤可能要执行很长时间，故在施加位移求反力的结果附近搜索效率更高。

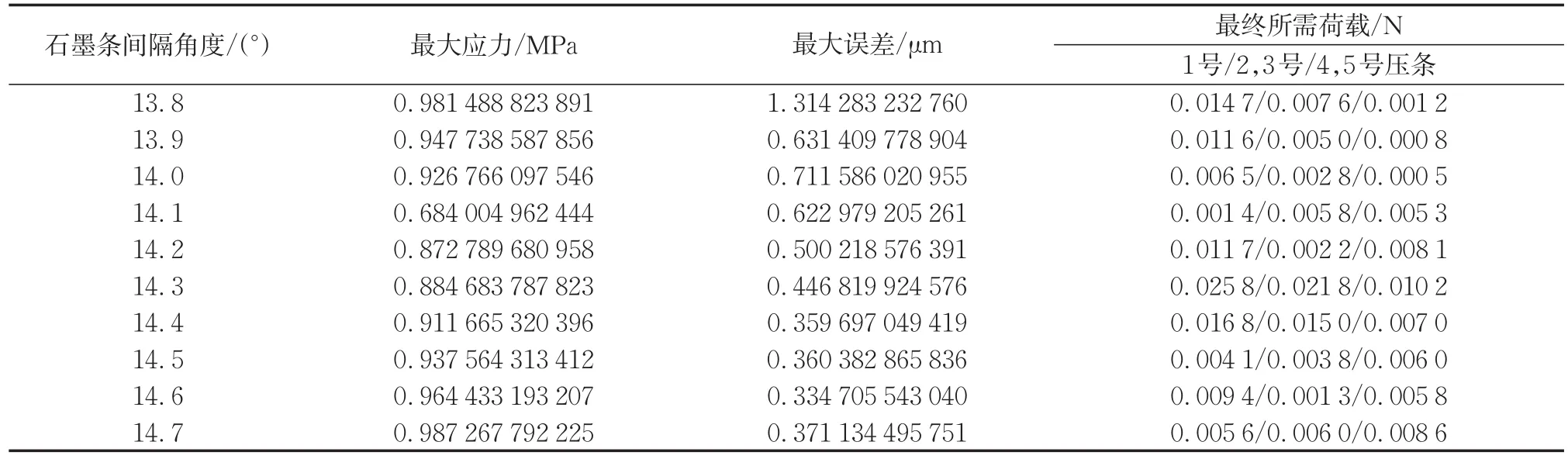
表5 不同石墨条间隔角度的计算结果Tab.5 Computational results of different angles of graphite strips

4.5 面形误差的进一步表示

以前的研究较为重视径向误差对像差的影响［7］。由光路图可知，影响镜面成像的质量不只是径向误差Δd，镜面倾斜角度的误差Δθ对镜面成像的质量也有一定影响，故面形误差实际上应当用如下关系式来表示（此处以主镜的误差为例）：

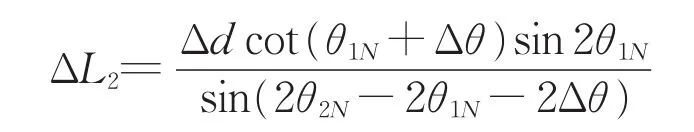
对于Δθ的求算，本文考虑用曲面拟合仿真后镜面得到的散点，装配相关参数与镜片厚度为0.4 mm的算例相同。具体算法如下：找到所求节点周围的点（边界点处理稍微特殊），对这些点进行二次曲面拟合，获得曲面方程，求曲面在此处的法向量，并与理想锥面的法向量作比较。所得的倾斜角误差分布图如图12所示。

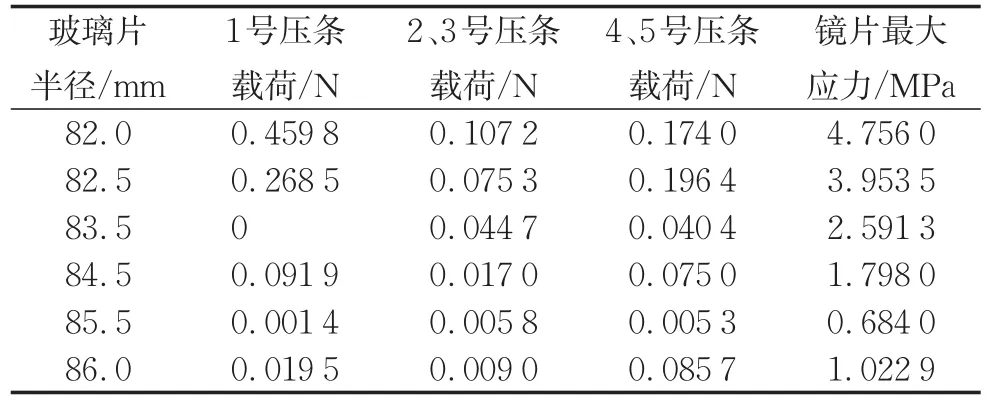
表6 半径82～86 mm镜片最优荷载组合及最大应力Tab.6 Optimal loads and maximum stress of mirrors with a radius from 82 to 86 mm

从倾斜角误差分布的情况来看，越往中间镜面的角度误差就越大，其计算精度与曲面拟合的程度有关。

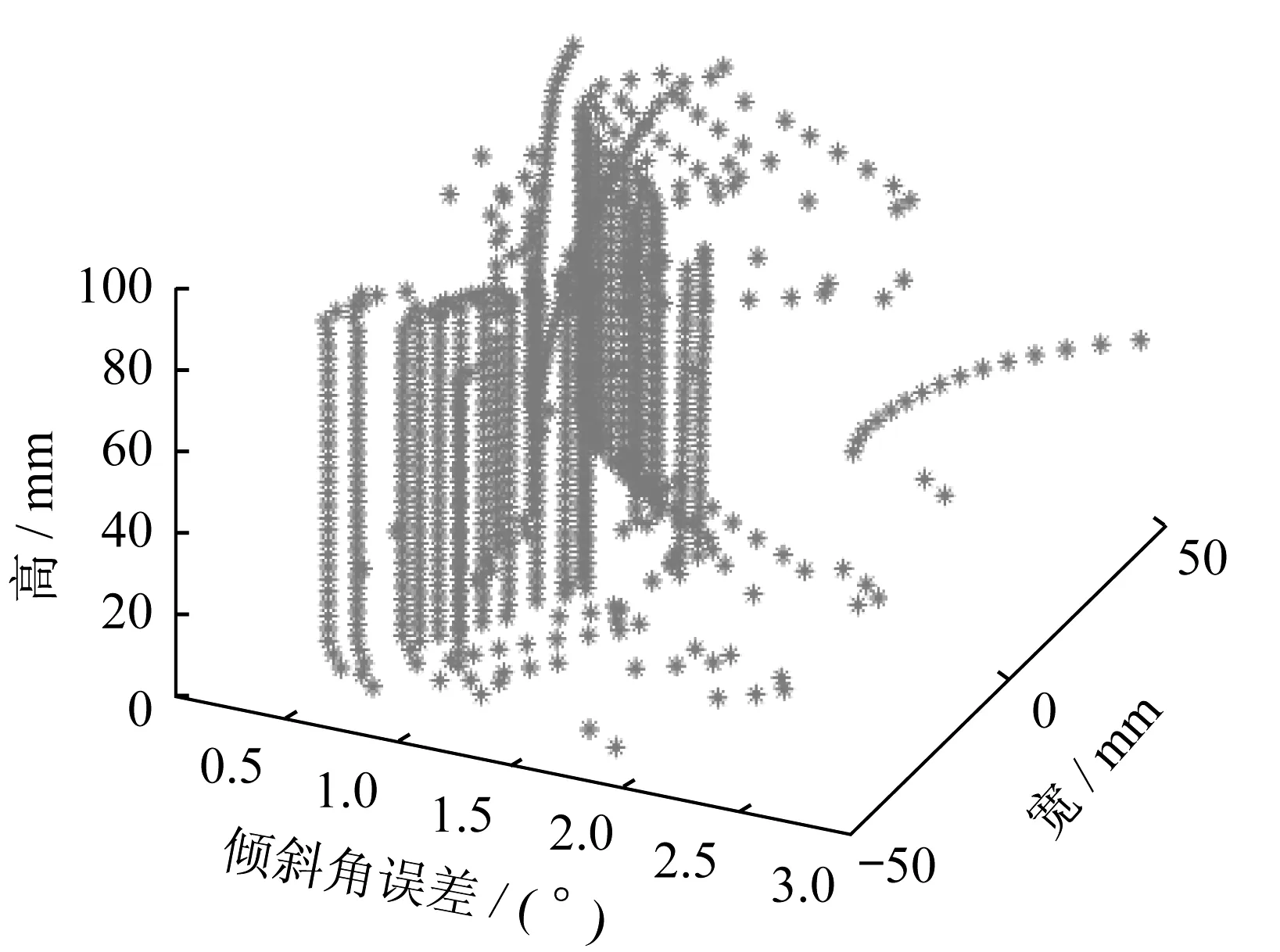
图12 倾斜角误差分布图Fig.12 Error of tilt angle

4 结论与展望

本文针对圆锥嵌套式Wolter-I型X射线聚焦望远镜镜片装配过程利用Abaqus建立了三维一体化建模和仿真算法流程，同时使用Python对Abaqus进行二次开发，提出了自适应建模计算方法，本方法可以有效提取各参数下的应力分布、面形偏差分布等结果。利用此算法流程对3种不同半径镜片进行加载，分析了前后端半径、镜片厚度、镜片曲率和装配载荷对结构面形偏差的影响，得到其面形误差与二维模型有着较大的不同，在镜片厚度偏小和偏大都会使得面形误差偏大，理想的厚度应在0.3～0.4 mm之间，石墨条间隔角度增加往往会减小面形误差，但要综合考虑各层镜面的情况等结论，并利用自适应算法自动地为不同半径镜片计算最佳装配载荷。在面形偏差的评估方面，本文提出了需要综合考虑面形径向偏差与面形倾斜角度变化的思想，并用曲面拟合的方法来估算镜面在某点处的法线方程，以此来对光路进行进一步的分析。此外，本文相应二次开发的算法和软件能够一体化地建模和仿真，可用于多层镜片计算，节约可观的实验成本和人工，具有良好的可拓展性和广泛的适用性。最后得到的最优镜片半径、最佳装配载荷和考虑多种面型偏差影响因素等研究结果，为提高装配工艺减少面形偏差提供了理论分析方法和装配指导方向。