高速公路冰雪湿滑路面车辆换道越线时间生存分析

柳本民，陈彦旭，管星宇

（同济大学 道路与交通工程教育部重点实验室，上海 201804）

车道变换是车辆行驶过程中的常见行为之一，车辆排队、拥堵、消散以及超车等过程往往伴随有换道行为。车辆换道行为与道路交通安全息息相关。据统计，车道变换引起的碰撞约占交通事故总数的4%［1］，其造成的交通延误达到所有碰撞事故的十分之一［2］。因此，车道变换给道路交通安全带来很大的负面影响。换道时程特征（包括换道持续时间、越线时间等）是研究换道安全性的关键指标，同时对于微观交通流模型的构建也具有重要意义［3］。

在换道时程特征研究方面，Worrall等［4］在1970年通过航空摄影的方法，对车辆执行换道所需时间进行测算和统计。此后，陆续出现一些研究尝试使用更加准确的测量手段，对车辆换道持续时间进行统计分析［5-6］，或研究某些因素对换道时间的影响［7-8］。Toledo等［3］通过交通监控视频提取车辆换道时间数据，结合微观交通仿真的需要，分别对小客车和货车换道时间进行建模。张良等［9］分别通过高空观测、车内观测和驾驶模拟3种方法，采集车辆换道时间数据，并对统计结果进行比较，认为通过驾驶模拟器可以得到更加准确、细致的数据，对于换道时程特征的研究更为适用。王雪松等［10］基于自然驾驶数据对变道切入过程的持续时间进行了统计，认为其基本符合对数正态分布，并较一般换道持续时间更为短促。

越线时间（time-to-line crossing，TLC）是指换道开始至车轮刚好越过车道线进入目标车道时刻的持续时间。换道冲突与换道车辆越过车道线的时刻关系密切，当车辆越过车道线开始进入目标车道时，对于目标车道后方车辆影响最为显著。因此，越线时间是开展换道安全预警的重要参数。很多学者尝试对其进行预测。Mammar等［11］基于三角几何关系分别提出直线段和曲线段TLC的计算方法。Winsum等［12］提出了TLC的两种估算方法，并比较了在正常行驶、正常换道以及驾驶员疲劳导致车道偏离3种情境下模型的估算精度。王畅等［13］、郑楚清［14］通过高次多项式实时拟合车辆换道轨迹，进而根据轨迹时间关系实现对TLC的预测，并利用实测数据进行验证。在此基础上，黎莉等［15］建立了营运车辆换道越线时间预测模型。

而在冰雪天气下，由于道路交通环境的复杂性，驾驶员对于车辆的控制能力以及对外界感知能力均有所下降，对换道安全距离更容易出现错误的估计。再加上换道行为本身的复杂性和风险性，使驾驶员很容易做出错误的判断或操作，导致车辆换道过程中追尾、侧向刮擦、斜向碰撞等交通事故频发，严重危及交通安全，降低了道路通行效率［16］。但基于气象环境的特殊性与安全性方面的考量，冰雪天气低摩阻系数路面交通数据采集困难，难以直接通过户外实车试验采集相关数据，故对冰雪湿滑路面车辆的换道行为特征缺乏必要的细化分析，这是一个亟待解决的问题。因此，本文基于高逼真驾驶模拟器，对冰雪等天气下的驾驶场景和路面行驶质感进行模拟，采集换道数据，对不同天气和路面条件下的车辆换道越线时间特征进行研究。

1 模型与方法

生存分析（survival analysis）起源于医学，是研究事件产生某一结果所经历的持续时间的一种统计方法。目前很多学者已经尝试使用生存分析解决交通领域的时间相关问题，如离散交通事故数据的分析［17］、交通延误［18］、交通出行时间［19］、交通事件持续时间［20］、交通拥堵持续时间［21-22］、非机动车闯红灯行为及忍耐时间［23］，以及作业区强制换道持续时间［24］等。

将生存分析方法应用于车辆换道时程问题，车辆换道行为的持续时间可以理解为“生存时间”。具体来说，将车辆开始换道作为研究的起点，车辆仍处于原车道则代表“生存”，一旦车辆越过车道线进入目标车道，车辆所处的车道状态改变，则事件结束。

1.1 车辆越线时间生存函数建模

生存分析的基本变量是非负的时间相关变量T，主要通过生存函数和风险函数描述T的分布特征。在车辆换道越线时间分析中，T是指从车辆开始换道至车辆越过车道线为止（事件开始并持续发生至产生结果）所持续的时间，车辆越过车道线即为事件发生的结果。

生存函数S(t)是指车辆开始换道后持续至时刻t仍未越过车道线的概率，其本质是累积生存概率，可表示为

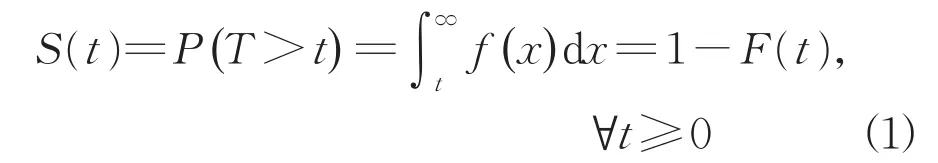
式中：T为越线时间；f(x)为T取值为时刻x的概率密度；F(t)为累积分布函数，表示从事件开始发生至t时刻已经出现结果的概率，也就是车辆换道开始至t时刻前或恰好在t时刻越过车道线的概率。

风险函数表示车辆换道已经持续至t时刻未越过车道线的条件下，在单位时间Δt内越过车道线的概率，其本质为条件生存概率h(t)，公式为

1.2 车辆越线时间半参数生存模型Cox

Cox模型是一种分析协变量对于生存时间影响的比例风险模型，可定量分析影响因素的作用强度和方向，得到各时刻生存状态改变的风险函数，从而得到多因素的生存时间函数。

车辆换道越线时间为T＞0，与T相关影响因素构成的协变量向量为X=[x1，x2，x3，…，xn]，影响程度通过协变量参数向量β=[β1，β2，β3，…，βn]来表示，X与β之间的函数关系以I(X，β)来表示，称为T的影响函数。在X的影响下，车辆越线时间的风险函数称为X前提下的条件风险概率，且

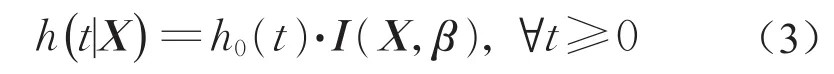
式中：h0(t)称为基准风险函数，即不受任何其他因素影响情况下（即I(X，β)=1）的风险函数。

根据Cox回归模型的性质，若βi＞0，说明xi是一个风险变量，对风险函数有正向影响，会增大风险水平，起到缩短车辆越线时间的作用；若βi＜0，则xi是一个保护变量，倾向于降低风险水平，起到延长车辆越线时间的作用；若βi=0，说明xi是车辆越线时间的无关变量。

结合生存函数S(t)与风险函数h(t)之间的数学关系，有

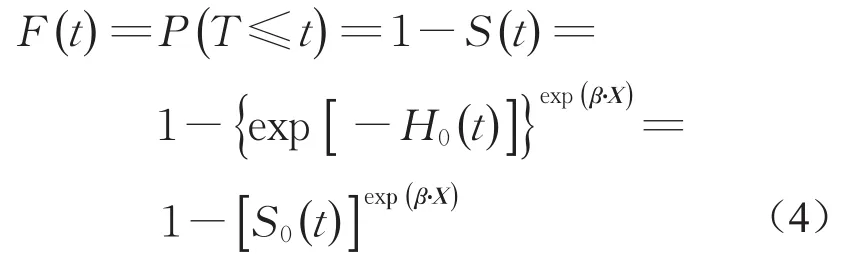
式（4）表示在影响因素X的作用下，车辆换道持续至t时刻已经完成越线的概率。

2 试验与数据采集

2.1 试验设计

2.1.1 试验设备

本试验依托同济大学道路与交通工程教育部重点实验室驾驶行为模拟系统（advanced car driving simulator，ACDS），如图1和图2所示，驾驶模拟舱动力系统开启时，可根据车辆实时行驶状态模拟车辆在x、y、z方向上的平移运动或绕轴转动，实现8自由度的运动仿真［25］。

图1 驾驶模拟器外观Fig.1 Exterior of driving simulator

针对冰雪湿滑路面场景，SCA Ne Rstudio 1.6驾驶模拟仿真软件能够有效模拟冰雪湿滑路面的车辆动态特性，结合ACDS强大的8自由度动力系统，更能反映冰雪湿滑路面的实际驾驶路感，从而刺激驾驶员做出相应的动态调整，试验数据更为真实可靠。同时，通过采用驾驶模拟试验，可规避冰雪环境实车试验时危险性高、试验误差大的不足，是本课题的有效研究方法。

图2 驾驶模拟器内景Fig.2 Interior of driving simulator

2.1.2 驾驶模拟试验场景搭建

高速公路相比一般公路车速高，车流量大，在冰雪等恶劣天气下，车速分布离散性增大，换道行为频发，具有较高的研究价值。本试验路段参照设计速度120 km·h-1的平原区高速公路设计，采用双向6车道，提供充足换道空间，车道宽度3.75 m，并按规范设置应急车道。

为控制试验变量，主线均为平直路段，包含准备段及4个试验段，各路段之间以匝道连接。准备段用于被试者提前熟悉操作，适应模拟环境，减少试验误差。4个试验段分别模拟晴天、雨天、降雪、结冰等4种天气状况。根据表1将路面摩阻系数分别设置为0.8、0.5、0.3、0.2，分别对应干燥路面、湿润路面、积雪或轻度压实雪路面、冰板或冰膜路面，其中干燥路面场景主要起对照作用。为避免摩阻系数突变影响试验数据，将摩阻系数变化点设置于各匝道段中部，匝道内部数据与本研究无关。各试验段视觉效果如图3所示。

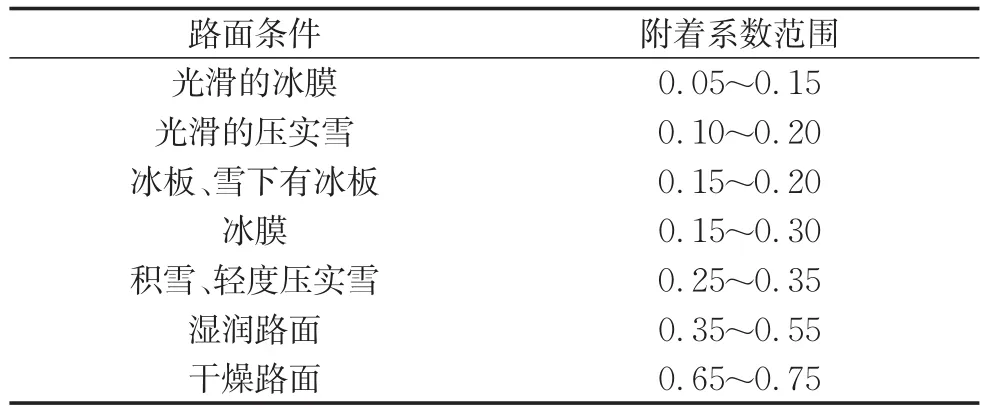
表1 不同状态下的路面附着系数［26］Tab.1 Adhesion coefficients of pavements under different conditions[26]

在交通流方面，本试验通过SCANeRstudio 1.6的swarm组件配置环境车辆，保证周围环境车辆与试验车辆的交互，环境车辆交通流密度约为25辆·km-1，流量约为600辆·（h·车道）-1，车型均为小型车，属中等密度。

图3 驾驶模拟试验仿真场景Fig.3 Scenarios of driving simulation experiment

2.1.3 试验流程

本试验共招募试验样本22名，包括学生、保安、出租车司机、教师等，其中男性18名，女性4名，均拥有驾照，并具备一定的湿滑路面驾驶经历。试验过程中，有2名男性出现驾驶模拟症，其余20名被试者适应良好。被试者的年龄、驾龄分布情况如表2所示。

表2 试验样本信息Tab.2 Information of experimental samples

试验中主线限速120 km·h-1，驾驶员在保证安全、舒适的前提下，可根据当前交通状况自由选择车道，产生换道需求时即可进行换道，避免刻意换道。换道过程中应遵守交通法规，根据自身驾驶习惯进行操作。

2.2 数据采集

试验采集数据包括：时间、行驶里程、车辆横向位置（与道路中心线或边界之间的距离）、道路平曲线半径、车道号、路面摩阻系数、行驶速度、三轴加速度、方向盘转角、方向盘转速、刹车踏板开合度、油门踏板开合度，以及周边环境车辆的相对位置、速度等。

经过对试验数据的判别和提取，本试验共采集有效换道数据1 042次，如表3所示。

换道越线时间数据总体分布情况如图4所示。越线时间平均值为2.98 s，小于2 s的比例为10.26%，约15%的数据大于4 s，超过70%的数据分布在2～4 s范围内。对越线时间数据进行正态分布检验，偏度系数为1.375，峰度系数为3.755，整体呈峰态较为陡峭的正偏态分布。

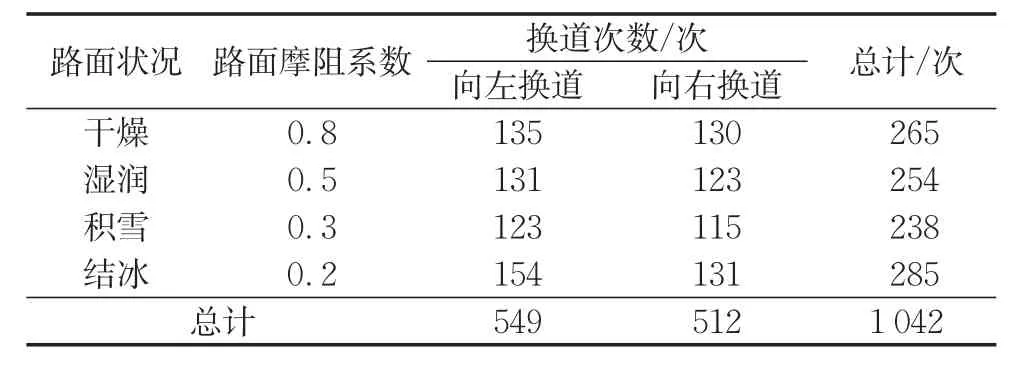
表3 换道数据统计Tab.3 Statistics of lane changing behaviors

图4 越线时间总体分布Fig.4 Distribution of TLC data

3 车辆越线时间指标分析

采用Kaplan-Meyer（K-M）非参数生存分析直接估计越线时间T的生存函数和风险函数，定量分析在某一特定影响因素下越线时间的分布特性。设通过驾驶模拟试验所采集到的有效换道数据共n组，包含越线时间数据n个，将数据按升序排列为t1≤t2≤…≤tn，则车辆的越线时间可估计为

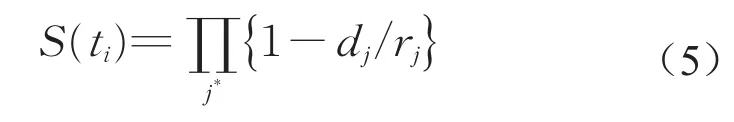
式中：S(ti)为车辆越线时间大于ti的概率；j*为满足条件tj＜ti的所有j的集合；dj为区间[tj，ti)内车辆完成越线的样本数；rj为截止至tj时刻车辆仍未完成越线的样本数。

变量选取应考虑在换道起点即可获得且具有代表性的参数，故选取摩阻系数、换道方向、跟驰状态以及换道起点车速作为分析变量。

3.1 不同摩阻系数下越线时间分布特征

将摩阻系数作为分类因子进行生存函数非参数估计，生存时间个案统计如表4所示。

表4 不同摩阻系数生存时间个案统计Tab.4 Statistics of survival time of cases at different adhesion coefficients

不同摩阻系数下的越线时间生存函数曲线如图5所示。生存函数S(t)是时间变量t的非增函数，在换道起始时刻（t=0），生存函数值为1，随着时间推移，生存函数值逐渐下降，并最终趋于0。生存曲线越陡峭，说明生存率降低速率越快，即该时段内车辆完成越线的样本数越多；生存曲线越平缓，说明生存率降低越缓慢，样本总体的越线时间就越长。由图5知，不同摩阻系数下生存曲线的总体走势相近，尤其是换道开始前2 s内，生存曲线重合度较高且趋势平缓，说明各组内在0～2 s内完成越线的样本数量都很少；至2 s时刻，各组内未完成越线的生存概率基本都在90%以上。换道开始2 s后，生存曲线下降速率显著加快，同时，不同摩阻系数组间的差异也开始体现，高摩阻系数（f=0.8，0.5）条件下生存曲线更加陡峭，车辆越线时间的总体水平较低；低摩阻（f=0.3，0.2）系数组则反之。同组之间，摩阻系数相对更低的一条生存曲线则处于上方，曲线走势更加平缓，说明车辆完成越线所需的时间更长。而后，高摩阻曲线约在4 s后开始逐渐趋于平缓，在这个时间点上，超过90%的样本车辆已经完成换道。而低摩阻曲线约在6 s后逐渐趋于平缓。

由表5给出的组间比较检验结果，p＜0.05，拒绝原假设，说明不同摩阻系数条件下车辆越线时间存在显著性差异。相同生存概率下，随着摩阻系数的降低，越线时间依次延长。在相同时间点上，越线时间的生存概率随摩阻系数的降低逐渐提高。

图6给出不同摩阻系数下的越线时间累积风险函数曲线。由图6可知，车辆越线时间的风险函数是时间t的增函数，即某辆车换道的持续时间越大，在下一时刻完成越线的概率就越大。摩阻系数越高，车辆在相同时间点上的“死亡”（即完成越线）风险越大。

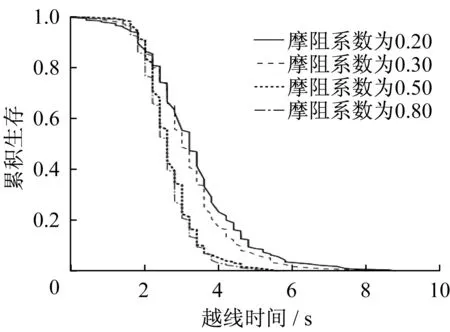
图5 不同摩阻系数下的越线时间累积生存函数Fig.5 Survival distribution function for TLC at different adhesion coefficients

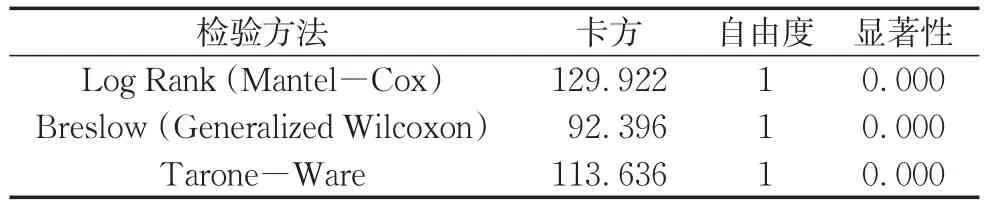
表5 摩阻系数组间总体比较检验结果Tab.5 Significant test of TLC at different adhesion coefficients

图6 不同摩阻系数下的越线时间累积风险函数Fig.6 Hazard function for TLC at different adhesion coefficients

3.2 不同换道方向越线时间分布特征

同理，对不同换道方向的车辆越线时间生存函数进行比较，结果如图7所示。可知，不同换道方向的越线时间生存曲线基本重合，且根据Log Rank假设检验结果，p＞0.05，即两者的越线时间无显著性差异。说明换道方向对于车辆换道越线时间的影响不显著。

图7 不同换道方向的越线时间累积生存函数Fig.7 Survival distribution function for TLC at different lane changing directions

3.3 不同跟驰状态越线时间分布特征

车辆的跟驰状态对于换道时程特征存在一定影响。研究表明，在驾驶员状态和车况良好时，车辆跟驰的安全距离一般为速度值（单位采用m·s-1）的1/2以上；当驾驶员和车辆状况不佳时，跟驰距离应当保持在速度值（单位采用m·s-1）的2倍以上［27］。样本数据中车速范围是14.99～135.06 km·h-1，考虑到冰雪等特殊路况的影响，取跟驰状态的距离界定范围为100 m，即当车辆正前方100 m内存在其他车辆时，认为试验车辆处于跟驰状态，定义正前车状态为1，反之正前车状态为0。

由图8知，当车辆处于跟驰状态时，生存曲线更加陡峭，说明车辆从开始换道至越线所需要的时间更短。在换道开始初期，这种差异并不明显，随着时间的推移，不同跟驰状态下的车辆完成越线的概率差异越来越显著。根据Log Rank假设检验结果，p＜0.05，拒绝原假设，当车辆处于跟驰状态时，其越线时间与非跟驰状态下存在显著性差异。

这说明，跟驰车辆做出换道决策的主要原因是前车行驶速度较慢，无法达到期望车速，驾驶员具有较为迫切的换道意愿。这种情况下后车车速往往大于前车，在TTC（time to collision，碰撞时间）的压力下，驾驶员倾向于采取更加果断的换道动作，以更快越过车道线。

3.4 不同车速下越线时间分布特征

车辆换道时的车速水平以换道起点时刻的瞬时车速表征，试验所获得的换道起点车速分布如图9所示，不同摩阻系数条件下起点车速的分布范围存在显著差异，高摩阻系数（0.8、0.5）条件下，样本分布离散性很大；而摩阻系数为0.3的条件下，车速明显降低，分布集中程度提高；摩阻系数为0.2的条件下，车速进一步降低至30～70 km·h-1范围内，峰度进一步提高。车速数据与实际相符，随着路面附着系数的减小，驾驶员出于安全考虑，表现出更低的车速选择意愿，期望车速显著降低。另一方面，由于可选择的车速区间受到挤压，在权衡效率与安全两方面的因素后，驾驶员倾向于选择既能保证安全又能获得效率的车速范围，行驶车速分布趋于集中。

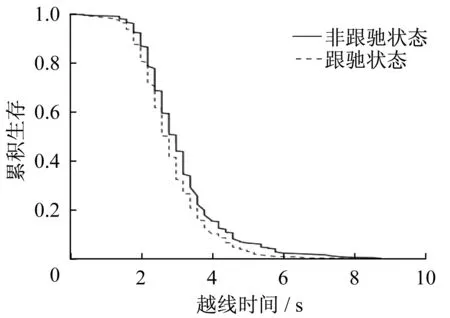
图8 不同跟驰状态的越线时间累积生存函数Fig.8 Survival distribution function for TLC at different car-following states

使用K-M非参数生存分析需将车速数据转化为有序分类变量。将起点车速值划定为［0，30）、［30，50）、［50，70）、［70，90）、［90，∞）km·h-15个等级，进行K-M非参数估计。

根据图10所示的生存曲线，不同车速水平下越线时间生存函数走势存在差异，车速越高，生存函数形状越陡峭，生存率下降越快；相同生存概率下，车速水平越高，车辆完成越线所需要的时间越短。根据非参数估计检验，p＜0.05，原假设被拒绝，说明行驶车速对车辆换道越线时间存在显著性影响。

图10 不同车速等级下的越线时间累积生存函数Fig.10 Survival distribution function for TLC at different speeds

4 车辆越线时间Cox比例风险模型及参数估计

非参数生存分析缺少对其他参数的控制，需假定其他影响因素是完全随机无影响的，也仅适用于对分类变量的分析。故采用生存分析中的Cox半参数估计方法进一步分析。除以上4个指标外，换道起点横向位置（物理意义为换道开始时刻车辆重心与目标车道线之间的距离）反映了车辆越线前所要经过的横向运动距离，与越线时间存在必然的联系。因此，结合车辆换道实际以及非参数生存分析结论，选取路面摩阻系数f、换道起点车速v、车辆跟驰状态fv以及换道起点横向位置d为协变量，建立Cox半参数生存模型。

协变量的相关性分析结果如表6所示。摩阻系数与换道起点车速之间存在较强的相关性，但考虑到两者均为车辆换道过程中的重要参数，对换道行为的影响机理也存在很大区别，故予以保留。

表6 协变量相关性分析Tab.6 Correlation analysis of covariates

基于式（6）对协变量参数β进行估计，进而使用导出乘积限估计的方法得出累积基准生存函数S0(t)。

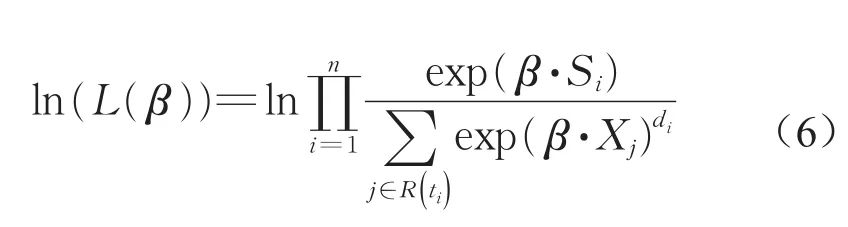
式中：L(β)表示β的偏似然函数；di为总样本中越线时间同为ti的样本个数；Si为该di个样本协变量的和。

车辆换道越线时间多因素Cox风险模型参数估计结果如表7所示，β列为各协变量的系数估计值，系数为正的变量对于风险率存在正向影响，对于越线时间存在负向影响；SE列表示该参数的标准误差；Wald列表示Wald检验统计量；Sig.列为显著性检验p值；Exp（β）列表示相对危险度，反映了在该因素影响下越线事件发生的风险概率变化。由表7可知，4个协变量的显著性检验p值均小于0.05，说明4类影响因素对于车辆越线时间影响显著。

表7 换道越线时间Cox模型参数估计结果Tab.7 Parametric estimated parameters of Cox model for TLC

根据参数估计结果，车辆在开始换道后t时刻完成越线的风险函数为

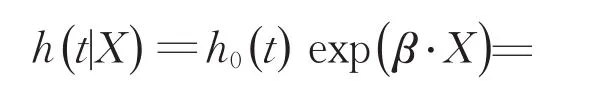
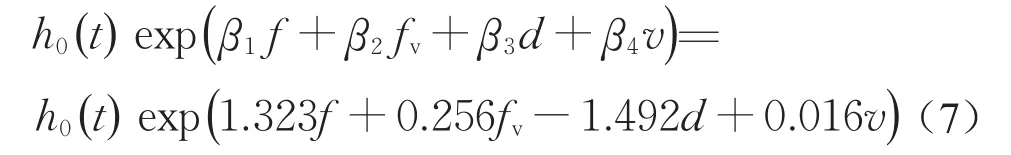
越线时间Cox比例风险模型为

根据相对危险度Exp（β）的估计结果，摩阻系数f每升高一个单位，越线时间的风险率提升为原来的3.76倍。在实际情况下，摩阻系数每升高0.1，风险率提高为原来的exp(1.323×0.1)=1.14倍，越线时间缩短。起点横向位置d每提高一个单位，越线时间的风险率降低为原来的0.23倍，越线时间延长。同理，处于跟驰状态的车辆相比非跟驰状态车辆在该时刻完成越线的风险概率提高为原来的1.29倍；行驶速度v每提高1 km·h-1，车辆完成越线的风险概率提升为原来的1.02倍。

5 结论

针对冰雪湿滑路面难以开展自然驾驶试验的现状，基于同济大学8自由度高逼真驾驶模拟系统，从试验设计、场景搭建等方面系统地提出冰雪、结冰等极端低摩阻情况下的驾驶模拟试验方法，在定性分析基础上，选取行驶车速、路面摩阻系数、跟驰状态、起点横向位置为指标变量，通过生存分析方法定量分析了多因素影响下的车辆换道时程特性，建立了车辆换道越线时间Cox半参数生存模型。结果表明，路面摩阻系数、车辆跟驰状态、行驶车速等指标对越线时间产生负向作用。路面摩阻系数每提高0.1，车辆在该时刻完成越线的风险概率提高为原来的1.14倍；处于跟驰状态的车辆在该时刻完成越线的风险概率是非跟驰状态车辆的1.29倍；行驶速度每提高1 km·h-1，车辆完成越线的风险概率提升为原来的1.02倍，均导致越线时间缩短。换道起点横向位置对越线时间具有正向作用，该指标每增加1 m，越线时间的风险率降低为原来的0.23倍，越线时间延长。此外，换道方向对越线时间并无显著性影响。