基于ARIMA 型的中国家禽出栏量预测

张莹，谷圣臣，潘俊池，贾永全

（黑龙江八一农垦大学动物科技学院，大庆 163319）

我国是世界家禽饲养大国，不仅养殖历史悠久，而且禽肉和禽蛋产量高。2018 年，我国禽肉产量达到1 994 万t，位居世界第二；禽蛋产量3 128 万t，位居世界第一[1]。2018 年受非洲猪瘟的影响，中国猪肉总产量呈断崖式下降，禽肉将成为我国第一大消费肉类。第二次世界大战之后，全球经济逐渐复苏[2]，畜牧业也得到了快速发展。1980～2018 年，肉类总产量由14 024 万t 增长到32 946 万t，增幅高达135%，禽肉产量由最初的2 078 万t 上升到12 025 万t，上升幅度高达479%，禽蛋产量由2 833 万t 上升到7 898 万t，上升幅度高达179%。可以看出，在全球范围内，禽肉和禽蛋消费量呈逐年上升趋势。

在2018 年的中国家禽年出栏量排行榜中，排名第一的是山东省，家禽出栏量突破20 亿只。其次分别是广州省、福建省、河南省和安徽省，广东省的家禽出栏量突破10 亿只，福建省也从5.71 亿只增长到9.15 亿只，河南省和安徽省分别为9.07 亿只和8.74 亿只。在2018 年中国禽蛋年产量排行榜中，排名第一的也是山东省，禽蛋产量为447 万t，在全国畜蛋总产量中占比高达14.3%，其次分别是河南省、河北省、辽宁省和江苏省，分别为414 万t、378 万t、297 万t 和178 万t。

中国共产党第十八届五中全会审议通过的《中共中央关于制定国民经济和社会发展第十三个五年规划的建议》[3]，旨在到2020 年我国全面建成小康社会，即经济持续稳定发展[4]。农业是一个国家经济发展的基础，畜牧业已经成为农业和农村经济的主导产业、拉动农民增收的主渠道、新农村建设的重要支柱[5]，家禽产业是畜牧业的一个重要组成部分，通过对家禽出栏量进行科学预测，从而对我国居民禽肉的消费能力有一个明确的认知。问题在于如何建立一个合理的模型来预测我国的家禽出栏量，同时在复杂的政治和经济环境中，政府和企业如何进行家禽的产业布局和生产规划一直是我们面临的难题。对家禽出栏量数据进行统计分析建立的ARIMA 模型具有预测效果好、拟合度高、数据利用充分等优点。运用ARIMA 模型对我国家禽出栏量数据进行统计分析，以期为家禽的产业布局和生产布局提供参考和依据。

1 ARIMA 模型简介

自回归差分移动平均（ARIMA）模型是由美国学者博克斯和英国统计学家詹金斯共同创立的[6]，ARIMA 模型能根据历史值来预测将来值[7]。ARIMA 模型常被用来分析时间序列问题，除此之外，还有指数平滑和GARCH 等方法，其中以ARIMA 模型精准度最高、拟合性最好。

ARIMA 包含三个部分，即AR、I、MA[8]，其中AR表示自回归模型，其中，AR 为自回归模型，从而通过历史值来预测将来值，用p 表示自回归阶数。I 表示差分，通过差分处理将相关程度大的信息提取出来，d 表示差分阶数。MA 为移动平均模型，它能使自回归模型中误差项的分布更加均衡，用q 表示移动平均阶数。

ΔdXt表示对预测值Xt进行d 阶差分，u 表示常数项，εt表示误差，ai表示自回归系数，Xt-i表示历史值，bi表示偏回归系数，εt-i为不同期的误差项。

2 建立ARIMA 模型的一般步骤

（1）平稳化处理，建立模型前，要求序列是平稳序列，即一个序列的均值、方差和协方差不随时间推移产生变化[9]。实际上，平稳的时间序列很少，大部分序列都不平稳，首先可以通过时序图判断法进行检验，时序图判断法是最直观的检验方法，通过观察时序图的趋势来判断平稳性。其次是自相关系数检验法，通过观察随着滞后阶数增加时，系数是否快速趋近于0，是否除了前三阶落在置信区间外，其他阶都落进置信区间内。最后是单位根检验法，通过将p 值与0.05 进行比较来确定序列的平稳性，如果数据不平稳，可以通过差分或取对数来使其满足平稳性条件[10]。

（2）白噪声检验，如果序列值之间互不相关，那就意味着这个序列的过去对于预测将来毫无意义，这种序列被称为白噪声序列。原始时间序列必须是一组具有相关性并且有规律可循的数据，此时，根据历史值来预测将来值才有意义。将p 值和显著水平进行比较，从而确定平稳序列的白噪声检验是否通过。

（3）模型的识别和定阶，利用最小信息准则，当BIC 值取最小时，p 和q 的取值为最佳系数，此时建建立模型所形成的预测公式最简洁，对娄据的拟合效果最好，从而确定p 和q。

（4）诊断检验和参数估计，进行白噪声检验时，取显著水平a=0.05，将p 值与显著水平进行比较，来确定残差是否为随机序列。同时对模型参数进行估计，并对估计值进行检验，确定参数估计的可信度。

（5）模型的预测，建立ARIMA（p，d，q）模型后，形成一个预测模型，从而根据历史值预测将来值。

3 ARIMA 模型的应用

3.1 数据的来源

选用1986～2018 年我国家禽出栏量数据（所有原始数据来自《中国统计年鉴》，表1），综合运用SPSS 和SAS 统计分析软件，旨在建立一个适宜模型，对2019 年的我国家禽年出栏量进行预测。

3.2 平稳化处理

从1986～2018 年我国家禽出栏量数据的时序图（图2）中可以看出，我国家禽出栏量数据呈指数上升趋势，通过取对数处理可以将指数上升趋势转化为线性发展趋势[11]，最后通过差分处理来消除线性上升趋势。从取对数并进行二阶差分处理后数据的时序图（图3）中可以看出，数据基本平稳，可近似看为平稳序列。

图1 ARIMA 模型建模流程图Fig.1 ARIMA model modeling flowchart

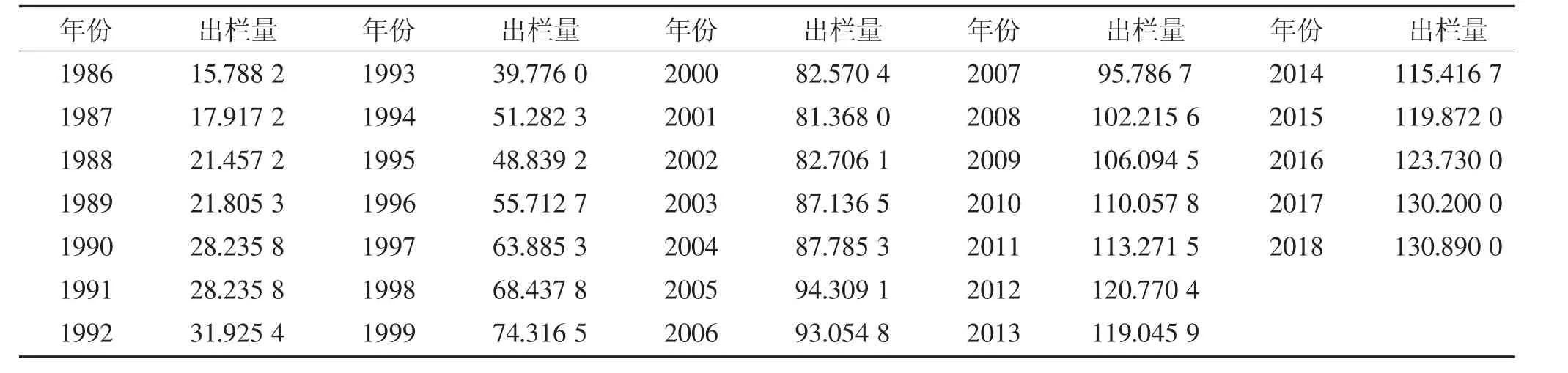
表1 1986～2018 年我国家禽出栏量统计表/亿只Table 1 Statistical table of poultry production in China from 1986 to 2018（100 million）

图2 家禽出栏量时序图Fig.2 Timing chart of poultry production

图3 取对数后二阶差分时序图Fig.3 Timing chart of logarithmic second-order differences

对取对数并进行差分的家禽出栏量数据进行自相关系数检验，从图4 和图5 中可以看出，当滞后数目增加时，自相关系数快速趋向于零。为了更加精确地确定检验的准确性，最后进行单位根检验法，将p值与显著水平进行比较，从而确定序列是否平稳。

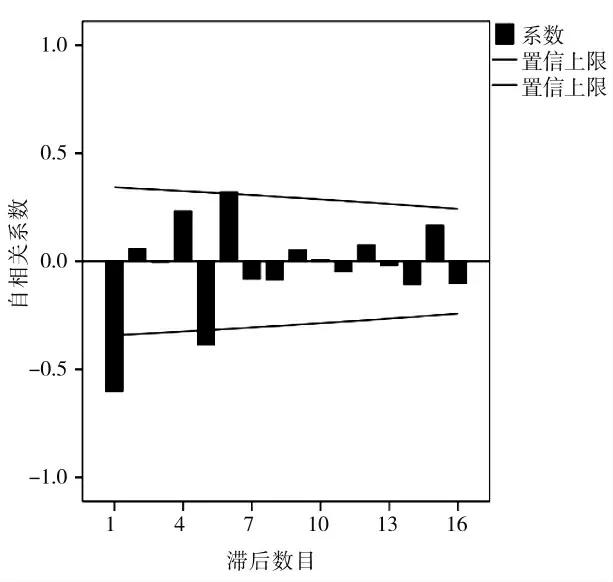
图4 自相关图（ACF）Fig.4 Auto Correlation Graph（ACF）

图5 偏自相关图（PACF）Fig.5 Partial Autocorrelation Graph（PACF）

从表2 中可以看出，在零均值、单均值、趋势这三种类型下，Tau 统计量的p 值均小于0.05，即二阶差分序列为平稳序列。

表2 二阶差分序列单位根检验表Table 2 Second order difference unit root test table

3.3 白噪声检验

当家禽出栏量数据确定为平稳序列后，就需要进行白噪声检验。从表3 中可以看出，取显著水平a=0.05，从滞后1 期一直到滞后16 期，p 值均小于0.05，所以该序列为非白噪声序列。

3.4 模型的识别和定阶

通过最小信息准则法来识别模型的类型和阶数，实验将p 与q 均小于等于5 的所有ARIMA 模型进行比较，由表4 可知，当p=2，q=0 时，BIC 值取最小，最小表值：BIC（2，0）=-6.704 2，此时建立的模型最简洁，对于家禽出栏量数据的拟合效果最好。由上文可知差分阶数d=2，最终确定ARIMA（2，2，0）模型。

3.5 诊断检验和参数估计

对模型的残差进行白噪声检验，从表5 可以看出，p 值为0.555，大于0.05，残差序列为白噪声序列[12]，即一组相关性小的随机序列。

对模型参数进行最小二乘估计，从而确定各个参数。表6 给出了模型参数的估计值和参数检验的结果，自回归系数a1的估计值为-0.873，自回归系数a2的估计值为-0.472，取显著水平ɑ=0.05，该模型t统计量的p 值小于0.05，即参数有效，该模型对该序列的拟合有效。

表3 二阶差分序列白噪声检验表Table 3 Second order difference sequence white noise test table

表4 MINIC 最小信息准则表Table 4 MINIC minimum information criteria table

表5 残差白噪声检验表Table 5 Residual white noise test table

表6 模型参数估计表Table 6 Model parameter estimation table

3.6 模型的预测

由ARIMA（2，2，0）模型：

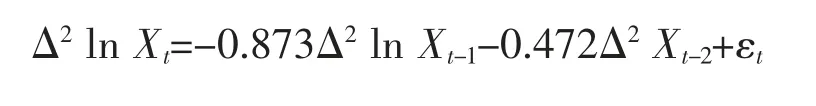
又因为：

序列Xt 的最终预测公式为：

从图6 可以看出，利用家禽出栏量数据所建立的ARIMA 模型对原始数据拟合效果较好。下面，对2019 年我国家禽出栏量进行预测，预测结果见表7。

图6 模型拟合效果图Fig.6 Effect of model fitting

表7 2013～2018 年实际值与预测值比较表/亿只Table 7 Comparison of actual and forecast values from 2013 to 2018（100 million pieces）

4 讨论

由于家禽出栏量受国家经济发展水平、家禽饲养数量、市场需求、政府政策和疾病防控等因素的影响。一个国家的经济发展水平影响家禽产业的生产和加工水平，而家禽的饲养数量和市场需求之间的供需关系影响畜禽产品价格，近而影响家禽出栏量。政府部门制定的方针政策影响畜禽产业的养殖规模和生产方向。疾病的防控也非常重要，疾病一旦发生，若管控措施不当会导致畜禽的大批量死亡，严重影响畜禽产业的供需平衡。从2013～2018 年实际值与预测值比较表（表7）中可以看出，利用该模型对2018 年我国家禽出栏量进行预测，预测值为134.49 亿只，而实际值为130.89 亿只，预测误差为2.75%，由此可见，所建立的ARIMA 模型具有较高的精准度。

许多学者从不同角度对预测方法进行比较分析，程诗广等[13]对比了ARIMA 模型和GM（1，1）模型在矿区开采沉陷上的运用，发现ARIMA（p，d，q）模型优于GM（1，1）模型，适用于矿区开采沉陷下沉量预测。刘夏等[14]运用ARIMA 模型和灰色马尔可夫模型对三亚市交通客流量进行预测，表明两种预测具有较高的精度。李志超[15]对比了ARIMA 模型、灰色模型和回归模型对上海市月度居民消费价格指数的预测，得出ARIMA 模型和灰色模型GM（1，1）适合进行短期项目预测且精准度相差不多，而一元n 阶多项式回归模型预测精度较差。宋媛媛等[16]应用ARIMA 模型和灰色模型GM（1，1）对湖北省痢疾发病数进行预测，通过拟合及预测评价指标的比较ARIMA 模型均优于GM（1，1）模型，可得ARIMA 模型对湖北省痢疾发病数的预测比GM（1，1）模型有较明显的优势，能更准确的处理时间序列类型的资料。林佳敏等[17]利用BP 神经网络和ARIMA 模型对污水处理厂出水总氮（TN）浓度进行预测，结果表明：BP 神经网络模型在训练集和测试集模拟结果的平均相对误差分别为15.9%和16.5%，模型预测结果的平稳性较差；ARIMA 模型对未来7 d 出水TN 浓度的时序预测平均误差为4.41%，预测精度较高。但该模型存在一个缺点，当预测时间延长时，预测误差会逐渐增大，所以ARIMA 模型只能用于短期预测。

家禽出栏量稳步上升，主要原因是人民生活水平的提高，饮食中对动物性蛋白的需求越来越大[18]。近年来，我国家禽产业发展迅速，一方面给国民提供了充足的肉制品和蛋制品；另一方面吸引大量农村剩余劳动力，增加当地农民的额外收入[19]。其次，近年来粮食供应充足，饲料原料丰富，在农村发展畜牧业，能够将粮食资源转化为肉、禽、蛋、奶、水产品等动物性食品[20]。最后，将饲养畜禽过程中产生的粪尿污水通过微生物发酵处理，杀灭其中的病原微生物，将粪污很好地转化为粪肥并施于农田，可以减少化肥的使用量，避免过度使用化肥对土壤、空气和水质造成的污染，使禽肉和禽蛋品质不断提高。虽然我国家禽业已经得到快速发展，家禽品种改良工作不断取得新的进步，但还存在核心种源长期依赖进口、良种繁育体系没有建立、集约化程度低、龙头企业带动不足和产品的深加工程度低等问题，只有解决好这些问题，我国家禽产业才能真正走向世界前沿。

5 结论

通过上述运算与分析可知，ARIMA 模型对原始数据拟合效果好、提取充分，预测公式简洁；模型简单有效，短期预测结果准确。利用ARIMA 模型预测我国2019 年和2020 年的家禽出栏量分别为135.08 亿只和138.58 亿只，根据该预测结果可见，我国家禽生产仍将保持持续发展的趋势，其定量的预测结果将为我国家禽业的生产规划和产业布局提供有益参考。