仿鸮翼叶片对轴流风机气动噪声特性的影响研究*
王 雷 李金波 黄榆太 马 列 刘小民
(1.西安交通大学能源与动力工程学院;2.广东美的制冷设备有限公司)
0 引言
轴流风机作为一种传统的流体机械,广泛应用于能源工程等国民经济的各个领域,也应用于空调、冰箱、吸油烟机等家用电器当中。这些家电设备在满足用户需求的同时,产生了较大的噪声污染,成为室内环境最主要的噪声来源之一。因此,如何降低轴流风机的噪声成为企业及科研人员关注的重要课题。
轴流风机的噪声问题始终未能得到彻底的解决,作为重要的噪声源,如家用风扇、空调用风机、工业通风设备等,对人们的生活产生了越来越多的困扰。同时,由于风机的广泛应用,对于噪声的研究也会产生显著的经济效益[1]。空气动力噪声是影响轴流风机稳定性及工作性能的主要原因。叶轮作为轴流风机的重要噪声源,通过传统的设计方法已经总结出了相关的降噪方案,如叶片穿孔法、采用倾斜整流片法、前掠叶片法以及不相等叶片间距等方式[2-3]。游斌等对空调室外机叶片采用尾缘凹陷设计后,对前缘局部加厚处理外,对叶片其他区域整体减薄,能够减小风轮质量,降低电机负荷,同时减弱转子尾迹,可以减小叶尖颤振,降低叶片旋转频率峰值噪声,同时改善音质[4]。但叶轮的静压和风量与原型相比均有所下降。由此可见,采用传统的降噪设计往往无法兼顾气动性能和噪声特性等多目标要求,因此有必要发展新的降噪理论和方案,从而为传统的降噪方案注入新的设计思路。
自然界中一些生物经过亿万年的进化,形成了具有环境适应性的躯体特征[5],因此仿生学作为一门新兴的学科,将生物学和工程应用紧密的结合了起来,通过生物解剖生成生物模型,然后进行仿生重构生成仿生模型,最后进行理论分析后进行工程应用,给人类的发明提供了源源不断的灵感和启迪。长耳鸮在飞行过程中不仅动作敏捷,而且在飞行的过程中产生的噪声很小,这与它的体貌结构密切相关,其头部也近似为圆滑的椎体,体表覆盖着波纹状层叠的羽毛可以减少摩擦和涡流噪声,且翅膀和尾部边缘的锯齿形状的非光滑边缘结构可以很大程度上减小其飞行过程中的涡流噪声。Lilley等研究发现在鸮类翅膀的前缘梳状和尾缘齿型结构能在捕食过程中显著降低噪声[6]。Graham等发现长耳鸮独特的翅膀构型具有明显的降噪效果[7]。此外研究还发现,鸮类低速飞行所消耗的能量远小于其他鸟类,长耳鹗在飞行过程中还具有静音飞行的特性,对于改善风机叶片的气动性能和声学特性具有借鉴意义,为提高风机性能、降低风机噪声提供了新的研究思路和方法[8]。
受到长耳鸮静音飞行的启发,本文针对直径为710mm的某工业用轴流风机,通过逆向工程提取长耳鸮翅膀沿翼展方向40%截面处翼型进行仿生重构,获得轴流风机叶片的翼型参数。采用数值计算方法研究了采用仿鸮翼型叶片对轴流风机气动性能和噪声的影响,提出了轴流风机降噪的有效技术途径。
1 仿生翼型的提取与重构
结合廖庚华等[9]提取的鸮翼典型截面的中弧线、厚度等几何特征,设翼型截面的中弧线坐标为Zc,厚度为Zt,通过拟合得到的翼型上下表面的坐标分别为Zupp和Zlow,得到各个截面处的翼型轮廓线如下:

中弧线分布如下:

厚度分布为:

其中,Z(c)max为中弧线分布的最大值;Z(t)max为中弧线分布的最大厚度,c为翼型弦长;η为弦长的相对位置坐标;Sn为待定系数,S1=3.936 2,S2=-0.770 5,S3=-0.770 5;An也是待定系数,A1=-29.486 1,A2=66.456 5,A3=-59.806,A4=19.043 9。
最大厚度分布公式为:

由于原型风机翼型截面的厚度分布为单圆弧分布,为了保证原型风机的气动性能,将上述鸮翼翼型的中弧线分布用原有风机翼型的单圆弧进行替代。针对特定风机某个回转面的投影半径为r的中弧线近似为鸮翼翼型的曲率半径,以满足对轴流风机不同弯掠角的设计情况,使仿生翼型的应用更具有普遍性。假定翼型的弦长为1,中弧线的圆心位置分布在翼型弦长中点的垂直平分线上,则中弧线分布规律如下:


图1 仿生翼型中弧线构建Fig.1 Mid-arc line of bionic airfoil
同时用比例系数来控制翼型的厚度分布系数,以原型翼型的最大厚度为基准,假定厚度分布的比例系数为ξ,则

提取长耳鸮翅膀40%截面处的厚度分布,如图2所示。考虑到长耳鸮翼型在尾部过于尖锐而导致的加工难度问题,因此在该40%截面处翼型的基础上提取该翼型弦长的前80%的厚度分布进行翼型重构,并将其应用在不同叶高处的回转面上,图3所示为仿生翼型在50%叶高处的截面的投影图。在重构翼型的基础上,从叶片根部到顶端等间距共截取了五个截面得到更加准确描述轴流风机叶片的翼型[10]。

图2 长耳鸮翅膀展向40%截面翼型图Fig.2 40%cross section of long eared owl wing

图3 仿生叶片50%叶高处重构翼型截面Fig.3 Reconstructed airfoil section at 50%of bionic blade height
2 数值计算模型
2.1 计算模型及定常流场计算
轴流风机模型如图4所示。主要部件有叶轮和导风圈,主要针对叶轮进行优化设计,采用CREO进行三维物理建模,对电机区和安装凸台部分及网罩等相应部分进行简化,图5和图6分别给出了几何重构后仿鸮翼叶片某回转截面的形状及整体数值计算域。

图4 风机模型图Fig.4 Diagram of fan model

图5 仿鸮翼叶片的局部示意图Fig.5 Partial schematic diagram of the bionic wing blade

图6 数值计算域Fig.6 Numerical calculation domain
针对研究的轴流风机,采用Workbench分别对轴流风机的内部流动区域进行网格划分。为了能够控制轴流风机各部件的网格尺寸,将轴流风机分为进口延长段、电机区、叶轮、出口延长段四个区域,然后分别进行了网格划分,各区域之间通过interface交界面进行连接。为了更好的控制整体网格数量,将进出口延伸段进行结构化网格处理,为了保证数值计算的准确性,在网格划分时,对主要部件的近壁面区域的网格进行了边界层加密,保证叶片表面的y+在1附近,满足大涡模拟对近壁面网格的要求。通过网格无关性验证后,最终整体轴流风机模型的总流域网格数约800万,进出口延伸段采用结构化网格,叶顶间隙区、电机区及叶轮区采用非结构化网格,叶轮区的网格数约560万,对叶顶间隙区的部分进行了局部加密,由于表面网格要满足紧凑声源条件,采用的计算频段为10 000Hz,计算得到的表面网格尺寸为3.4mm,取表面网格尺寸为3mm,同时共施加10层边界层,第一层网格高度为0.02mm,保证表面的y+大部分均小于1来满足大涡模拟对近壁面网格的要求。
3 数值模拟计算及分析
3.1 流场与声场计算模型
定常流场计算采用商业软件Ansys Fluent对轴流风机的内部流场进行相应的数值计算,文中所选用的湍流模型为Realizablek-ε模型,壁面采用无滑移边界条件,旋转区域采用MRF运动参考系模型,旋转速度设为969r/min。求解算法选择SIMPLEC算法,由于网格均为六面体网格,因此梯度求解选择常用的Green-Gauss Cell Based;动量方程、能量方程和湍流耗散方程均采用二阶迎风格式,收敛残差设为10-4。考虑到精度要求,动量方程、能量方程和湍流耗散方程均采用二阶迎风格式[11],相对于一阶格式来说,二阶迎风格式具有更小的截断误差。进口总压为101 325kPa,出口静压为101.325kPa。由于大涡模拟能更加准确的捕捉脉动效应对流场的影响[12],因此在稳态流场计算的基础上,非定常流场计算目前应用广泛的是大涡模拟(LES)[13]结合FW-H声类比方程方法,即由大涡模拟获得非稳态流场,再由FW-H方程将获得的非稳态流场信息转化为声场信息,较易快速得出结果,有利于工程实现[14]。最后通过快速傅里叶变化将时域信号转换为频域信号,得到频谱、声压级等数据信息。由于波长远大于风机的特征尺寸,因此噪声计算中可以忽略导风圈和叶轮之间噪声的反射、衍射和散射[15]。
由下式确定非定常计算的时间步长为:

式中,Δt为时间步长,f为FFT变换可捕获的最高频率。在非定常流场及噪声计算过程中,亚网格尺度湍流模型为Wall,压力离散格式采用二阶迎风格式,压力-速度耦合采用PISO算法,动量方程为二阶中心差分格式,时间离散采用二阶隐式差分格式,边界条件与定常计算设置保持一致。考虑到轴流风机的噪声主要集中在中低频区域,因此将计算频段设定0~10 000Hz,得到非定常计算过程的时间步长为5×10-5S,满足CFL条件[13],经过傅里叶变换之后捕捉到的最高频率为10 000Hz,每个时间步长的最大迭代次数设定为50步,在每个计算时间步长内,当残差小于1×10-4判定为收敛。

图7 风洞测试实验室Fig.7 Wind tunnel testing laboratory

图8 半消音噪声测量实验室Fig.8 Noise semi-anechoic measurement laboratory
气动性能测试的实验装置及方法根据《GB/T 1236-2010工业通风机用标准化风道进行性能试验》与《AMCA210-2007通风机额定性能实验的实验室方法》进行,气动性能实验测试装置为LW-9293-600全自动风机风电性能测量装置,测试方法采用AMCA 210-99风扇测试系统。将非定常计算得到的稳定流场作为FW-H声学方程的输入条件,为了更好的和实验进行对比,并按照《GB/T 2888-2008GB/T2888-2008风机和罗茨风机噪声测量方法》中轴流风机规定的测试点设置噪声接收点,噪声接收点设在距离风机水平进口中心处1m,对应接收点坐标位置设置为(0mm,-1092.31mm,0mm)。噪声测试实验在半消音室内进行,图7和图8分别为气动性能测量实验装置和半消音室测量装置,实验测试结果与数值模拟结果的对比如表1所示,风量值相对误差为1.2%,噪声值相对误差为2%,数值计算误差整体控制在5%以内,满足工程设计和对计算精度的要求。

表1 原型风机的数值模拟和实验验证Tab.1 Numerical simulation and experimental verification of the prototype fan
3.2 流场结果分析

图9 原型风机与仿鸮翼翼型风机的静压比较Fig.9 Comparison of static pressure between prototype fan and the bionic owl profile fan

图10 原型风机与仿鸮翼翼型风机的效率比较Fig.10 Comparison of efficiency between prototype fan and the bionic owl profile fan
图9和图10分别为原型风机与仿鸮翼翼型风机在实验测试工况范围内的静压和效率折线图。仿鸮翼风机在整个运行工况内的静压均有所提升,说明仿鸮翼叶片的做功能力进一步提升,但由于其独特的厚度分布方式使得扭矩也同步增加,因此仿鸮翼叶片风机整体的效率比原型风机有小幅度的下降。在大流量及高效点的效率区别不大,从而保证了翼型在整个工况范围内气动性能基本保持不变,这与鸮翼略低的气动性能及优良的降噪特性保持一致。
静压分布云图如图11和图12所示,原型风机的静压分布梯度范围较为狭窄,当气流流经叶片表面时容易造成压力脉动,而仿鸮翼翼型风机的压力过渡区域相对较为和缓,压力梯度分布更为均匀,不容易引发由于叶片表面的压力差而引起的旋涡噪声;原型风机在叶尖处吸力面和压力面的梯度较大,容易引起叶顶泄漏涡的进一步脱落,从而造成叶片叶尖涡的能量对整体声压级的贡献度增加。从图13~图14可以看出,气流在从吸力面向压力面过渡的过程中,在叶片吸力面区域形成了较大的逆压旋涡,从而造成气流在叶尖处的脉动增加。仿鸮翼叶片的气流流经叶片时过渡较为平缓,流线也较为均匀,流线整体从吸力面流向压力面时形成较为均匀的旋涡然后平稳流向压力面,使得气流在叶尖处的脉动情况减弱,声能辐射也相对较小。

图11 原型风机50%叶高截面处的静压分布Fig.11 Static pressure distribution at 50%blade height section of prototype fan

图12 仿鸮翼翼型风机50%叶高截面处的静压分布Fig.12 Static pressure distribution at 50%blade height sectionof the bionic fan inspired by owl wing

图13 原型风机50%叶高截面处叶顶流线图Fig.13 Streamline near the tip at the 50%blade height section of the prototype fan
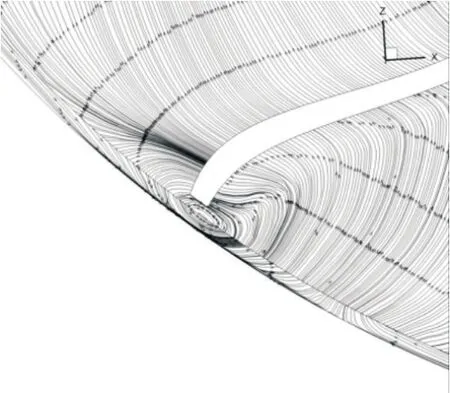
图14 仿鸮翼翼型风机50%叶高截面处叶顶流线图Fig.14 Streamline near the tip at the 50%blade height section of the bionic owl profile fan inspired by owl wing
3.3 声场结果分析
表2给出了原型风机与仿鸮翼风机的数值计算对比结果,从表中可以看出,在同转速下仿鸮翼风机的风量提升了4.6%,且总体声压级降低了1.41dB。在风机进口区域1m处监测点的声压级频谱如图15所示,从图中可以看出在4 000Hz频段以后的声压级逐渐减小。总声压级采用A计权,在中低频区域的噪声特性影响更为显著。结合人耳的听觉范围与计算效率和精度,本文将计算的频段范围设定为0~10 000Hz。可以看出在整个计算频段内仿鸮翼叶片的声压级都有所降低,尤其在低频区域的降噪效果更为明显,这与鸮翼的低噪飞行特性保持一致。原型轴流风机的叶片通过频率为80.75Hz,从计算数据可以看出对应的原型风机的基频声压级为31.20dB,而仿鸮翼轴流风机的基频声压级为26.77dB。可以看出采用出仿生翼型使轴流风机在基频处的降噪幅度约为4.43dB,从频谱图可以看出,轴流风机叶片的离散噪声和宽频噪声均有所降低,且在1 000Hz频段左右的降噪效果显著,整体表现为气流在流经叶片时变化更为缓和,对叶片表面的冲击强度减弱,从而有效降低了轴流风机叶片与导风圈之间的非定常相互作用。

表2 原型风机和仿鸮翼翼型的数值模拟对比Tab.2 Numerical simulation of the prototype fan and the bionic fan inspired by owl wing

图15 声压级频谱Fig.15 Sound pressure level spectrum
图16给出了原型风机和仿鸮翼风机的功率谱密度分布,从图中可以看出,原型风机与仿鸮翼翼型风机的噪声能量主要分布在整个计算频谱的中频区域,说明轴流风机的远场噪声在中低频区域的贡献较大。原型风机的功率密度的峰值约为仿鸮翼翼型叶片峰值的2倍,尤其在1 000Hz频段左右,仿鸮翼叶片的噪声能量降低的更为明显,说明仿鸮翼翼型叶片的厚度分布主要在中频区域的降噪效果更为显著。图17所示为原型风机与仿鸮翼风机的A计权的1/3倍频图,可以看出,轴流风机气动噪声表现出明显的宽频特性,且在整个计算频段内具有较为明显的降噪效果,特别是在1 000~2 000Hz频率范围内降噪效果更为明显。宽频噪声的降低说明气流在流经叶片时产生附面层的以及旋涡脱落引起的压力脉动程度减弱,而离散噪声的降低则表明气流来流的不均匀和不连续性减弱,与叶片的来流情况和叶顶间隙密切相关。

图16 功率谱密度Fig.16 Power spectral density

图17 A记权1/3倍频图Fig.17 1/3-octave band sound pressure spectrum dB(A)
声压时均脉动值[17-18]被定义为静压对时间偏导的均方根值,能反映出叶片表面上声源强度的大小。从图18与图19可以看出原型风机叶片表面的声源强度的最大值分布在叶片前缘区域及叶尖部分,说明气流在经过叶片表面时由于叶片截面翼型的作用引起前缘局部区域的流动分离恶化,导致叶片前缘局部产生的涡流与二次流加剧。由于气流在流经吸力面向压力面时叶顶泄漏涡的脱落也是重要的噪声源,叶顶间隙的流动对于流场和声场都具有非常重要的影响,原型叶片叶尖部分在前缘区域有叶尖小翼的产生抑制了部分旋涡脱落而引起的声压脉动,但该叶尖小翼在接近尾缘部分的设计较为平缓,基本上没起到使气流平稳进行过渡的作用,因此在叶尖后半区域的流动分离加剧造成了该处的声压波动强度较大。而仿生翼型独特的厚度分布使得气流在流经叶片前缘时较为平稳,能够延迟叶片表面的流动分离现象,从而使得叶片前缘区域的声压脉动强度减弱,但在接近尾缘部分,由于旋涡脱落的影响,使得尾迹涡仍然成为叶片表面的一部分噪声源,下一步可从控制叶片的尾迹涡方向出发进一步控制翼型整体表面的噪声源。从叶尖处的声压脉动图可以看出,仿鸮翼叶片的声压脉动范围区域进一步减弱,向翼型尾缘方向延伸,这是由于原型翼型的中部较厚,气流在流经叶片表面时容易在该处产生流动分离,加剧了垂直于叶片表面上的旋涡脱落,使得声场的噪声辐射能量进一步增加。

图18 原型叶片表面的风压脉动时均图Fig.18 PRMS distribution on the surface of the prototype fan

图19 仿鸮翼叶片表面的声压脉动时均图Fig.19 PRMS distribution on the surface of the bionic blade
4 结论
通过对原型叶片翼型的优化设计,以自然界具有独特静音飞行能力的鸮翼做为仿生原型,采用数值计算方法研究了仿鸮翼轴流风机气动性能及噪声特性,得到的主要结论如下:
1)仿生翼型的应用能够保证风机在宽工况范围运行时的整体气动性能,且在整个计算工况内静压都有提升,效率呈现小幅下降特性。这是由于轴流风机的效率与翼型的升阻力密切相关,而长耳鸮与滑翔类鸟类相比,飞行能力表现不突出,其主要特点体现在优异的降噪特性。
2)在叶尖处,仿鸮翼叶片的声压脉动范围区域减小,且向翼型尾缘方向延伸,这是由于原型翼型的中部较厚,气流在流经叶片表面时容易在该处产生流动分离,加剧了垂直于叶片表面上的旋涡脱落,使得声场的噪声辐射能量进一步增加。
3)仿鸮翼型独特的厚度分布使得气流在流经叶片前缘时较为平稳,能够延迟叶片表面的流动分离现象,从而使得叶片前缘区域的声压脉动强度减弱。但在接近尾缘部分,由于旋涡脱落的影响,尾迹涡仍然成为叶片表面重要的噪声源。因此,可以从控制叶片尾迹涡的角度出发,进一步抑制仿生翼型尾缘涡的脱落,达到降低轴流风机噪声的目的。

