轴流压气机数值模拟中复杂湍流模型的对比研究

钟艺凯 杨金广 张 敏 杨 帅 刘 艳 王春雪

（1.大连理工大学能源与动力学院；2.北京动力机械研究所）

0 引言

随着计算机技术的快速发展和数值计算方法的日益完善，计算流体力学（CFD）技术在叶轮机械中的有着越来越广泛的应用，其低廉的成本、高效的性能，使叶轮机械在设计研究过程中减少了大量的实验成本[1]。如宋国兴等[2]对轴流压气机进气旋流畸变进行仿真研究，陈振毅[3]等采用数值模拟方法研究了轴流压气机近失速工况下轴向间隙对径向流的影响，都获得了准确的结果，由此可见数值模拟在叶轮机械中的应用是准确可靠的。对于叶轮机械内部流动的数值模拟，主要是采用求解雷诺平均N-S方程（RANS）对其进行数值模拟。由于雷诺应力项的存在使得RANS方程不封闭，科学家根据湍流运动的基本规律发展了使方程组封闭的湍流模型，促进了湍流理论应用的发展。自1970年以来，湍流模型的研究得到了快速发展，先后建立了零方程、一方程、两方程及雷诺应力模型等湍流模型。虽然这些湍流模型能很好地捕捉到一些流动现象，但是其适用性都有一定的限制，其在叶轮机复杂流动数值分析中的适用性、精度以及稳定性等尚无定论，有必要进一步研究[4]。

本文以Durhum静子叶栅和NASA rotor37压气机转子为研究对象，基于所开发的CFL3D_Turbo数值计算平台，研究了B-L，S-A，Chien k-ε，SST k-ω和k-ε-Rt五种湍流模型计算的结果，重点考察了不同湍流模型的数值计算精度、流场细节捕捉程度以及湍流模型计算稳定性的影响。

1 求解器开发

本文求解器基于经过广泛验证的CFL3D开发而成，所采用的控制方程组为直角绝对坐标系下的三维雷诺平均Navier-Stokes方程组，其控制方程[5-6]可以表示为：

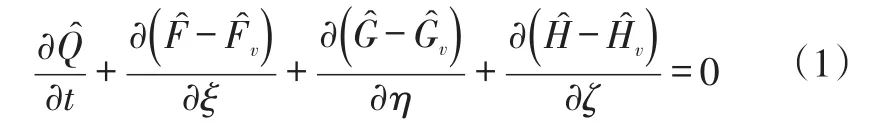
式中，t为时间；ˆ为守恒变量；为无粘通量；为粘性通量。

控制方程组空间离散格式采用通量差分分裂的Roe[7]格式进行离散，时间项采用近似因子分解法进行迭代求解，采用当地时间步长、多重网格以及残差光顺技术加速收敛。

本文对CFL3D经过适应性改进，形成专用于叶轮机械计算的CFL3D_Turbo数值计算平台。主要改进包括：1）开发了匹配的前处理模块。目前采用的策略是读取商用软件的网格生成结果，这里选用NUMECA软件包中Autogrid5模块。通过读取Autogrid5生成的网格文件，对其进行边界条件分析和坐标系转化，另存为CFL3D_Turbo识别的网格文件格式；2）改进了原求解器。主要有增加旋转域模拟能力，添加适合于圆柱内流计算的边界条件等；3）开发了较为完备的后处理软件。

2 湍流模型

2.1 B-L模型

B-L模型[8]是在C-S模型的基础上改进而得到的一种代数模型，它不仅适用于边界层的计算，还能应用于N-S方程中，因其应用简单且有相当的精度，所以其在工程领域中应用广泛[9]。下面给出其湍流粘性系数计算式：

其中，y为到壁面法向距离；ycrossover为内、外层粘性相等时y的最小值。其中内层粘性计算公式为：

式中，l为混合长度；ω为旋度。

外层粘性计算公式为：

式中，K为Clauser常数；CCP为附加常数。

2.2 S-A模型

S-A模型[10]是一种基于经验和量纲分析，建立了求解湍流粘性的输运方程，主要是针对简单流动而逐步发展起来的湍流模型，它对压力梯度边界层也有较好的预测。其输运方程如下：

式中，Gѵ为湍流粘度生成项；Yѵ为湍流粘度耗散项；Sѵ为源项。湍流动力粘性系数的计算公式为：

2.3 Chien k-ε模型

Chienk-ε模型[11]是一种低雷诺数模型，将泰勒级数展开技术用来处理固体壁附近的动能及其耗散率，同时它具有良好的经济性和计算精度，主要应用于各种管道流动和边界层流动。其输运方程为：

式中，P为湍流生成项；C1，C2，f1和f2为常数。湍流动力粘性系数计算公式为：

2.4 SST k-ω模型

SST k-ω模型[12]是Menter在标准k-ω模型的基础上进行改进和发展出来的，它考虑了近壁区逆压梯度边界层中的主剪切应力的传递，并将Bradshaw提出的主剪切应力与湍流动能成比例的假设引入到涡粘性的定义中，这使得它在近壁区逆压梯度和分离流动的计算有更好的预测精度，能够有效的预测逆压梯度条件下的流体分离的开始点和分离区的大小。其输运方程为：

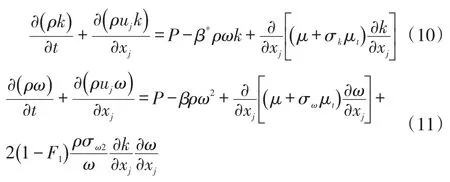
式中右侧前三项分别为生成项、耗散项以及扩散项，ω方程中第四项为交叉扩散项。湍流动力粘性系数的计算公式为：

2.5 k-ε-Rt模型

k-ε-Rt模型[13]是由湍动能k方程、湍流耗散率ε方程以及无阻尼涡粘度Rt方程三个方程共同组成。这个模型在湍流耗散率ε方程中加入了一个额外的源项，旨在提高非平衡流区域的耗散率ε水平，这样可以降低动能和长度尺度以此来改善对逆压梯度流的预测，其具有很强的数值鲁棒性且易于使用。下面给出它的输运方程：

式中，P为湍流生成项；E为耗散率ε方程中的附加源项；Cε1，Cε2，Cε3，C1，C2，C3，f1，f2为常数。其中湍流粘性系数计算公式为：

3 算例与分析

3.1 Durham压气机叶栅

Durham压气机叶栅为低速压气机平面叶栅，其采用可控扩散叶片。在模拟中进口总温为293.15K，进口总压为107 000Pa，进口气流角为37°；出口给定轮毂处静压97 000Pa，其余位置处静压由简单径向平衡方程得到。本算例计算网格如下图1所示。

图1 Durham叶栅网格Fig.1 Durham cascade grid

首先对比CFL3D_Turbo和NUMECA都采用S-A模型计算的出口处参数分布，证明二者得到了相同的结果，如图2所示，确认了求解器的正确性。出口总压的吻合证明二者计算得到的叶栅损失特性基本相同；而静压分布的一致性则表明气流偏转能力预测的正确性。

图2 出口边界条件对比Fig.2 Comparison of outlet boundary conditions

1）流场分析

将B-L模型，S-A模型，Chien k-ε模型，SST k-ω模型和k-ε-Rt模型湍流模型应用到Durham压气机叶栅数值计算中，得到了马赫数、静压、温度等在流场中的分布情况。由于缺少Durham压气机叶栅实验流场数据，所以将各模型计算得到的流场与NUMECA计算结果进行对比。图3给出Durham压气机叶栅50%叶高处S1流面的马赫数分布，然后对各湍流模型计算得到的流场进行分析和对比，可以看出，气流以较高的速度进入通道中且进口到叶栅前缘部分马赫数分布均匀，五种模型对这一区域的马赫数预测基本一致，且与NUMECA计算结果相同。当气流流经尾缘处，出现流动分离，形成低速区，产生尾迹。从计尾迹区域可以看出，在数值上基本一致，k-ε-Rt模型计算得到的尾迹区域偏大，与NUMECA的结果较为吻合。

图3 50%叶高S1流面马赫数云图Fig.3 Mach number contour at 50%span

2）压力系数分布

为了定量对比不同湍流模型对叶轮机械数值模拟结果的影响，将各湍流模型计算得到的Durham压气机叶栅表面的静压力进行处理，得到叶栅表面压力系数及其分布，将处理后的结果与NUMECA的计算结果和实验数据进行对比，叶片表面压力系数计算公式为：

式中，p为叶片表面静压；p01为进口中截面处总压；p2为出口中截面处静压。

从图4中可以看出，本文所计算得到的结果与实验数值以及NUMECA计算得到的结果分布趋势基本一致，数值吻合度也很高。在20%叶高处靠近前缘的压力侧，各湍流模型与实验数值的分布差距较大且过低预测了前缘处的压力系数，而在吸力侧SST k-ω和k-ε-Rt湍流模型的模拟数值与实验数值完全吻合。同时在压力侧SST k-ω和k-ε-Rt模型得到的模拟数值与实验数值吻合度很高，其对压力侧的流动预测具有很高的精度；而在吸力侧各模型的模拟数值与实验数值分布也是基本一致的，其中k-ε-Rt模型计算得到的结果与实验数值有很好的吻合度，在叶栅后半段的压力系数分布中，Chien k-ε和SST k-ω模型与实验数值有着很好的吻合度。在50%叶高处，各湍流模型计算得到的压力系数分布与实验数值分布趋势是一致的，k-ε-Rt模型预测的表面压力系数在压力侧和吸力侧与实验数值都最为吻合，而在压力侧靠近前缘位置处S-A模型计算得到的结果与实验数值偏差最大，在压力侧和吸力侧后半段Chien k-ε模型预测的数值与实验数值误差相对较大。在70%叶高处，各模型在叶栅前缘处的压力系数预测相对较差，而在压力侧B-L，S-A以及k-ε-Rt模型所预测的数值与实验数值十分吻合；Chien k-ε模型计算得到的叶栅表面压力系数分布误差相对较大。在90%叶高处，各模型预测的压力系数值与实验数值的分布趋势基本一致，S-A模型对压力侧的计算结果相较于其它四种模型更接近于实验数值，而k-ε-Rt模型在吸力侧预测的数值与实验数值更为吻合，但是各模型对靠近前缘处的静压系数预测都偏小。在95%叶高处，各模型计算得到的压力系数与实验数值的分布趋势是基本一致的，但是数值上有一定的误差，同时从图中可以看出NUMECA计算得到的结果与实验数值更为吻合，而SST k-ω和k-ε-Rt模型得到结果的误差相比大一些，这可能是由于未给定进口端壁边界层的缘故。

图4 表面压力系数对比Fig.4 Comparison of surface pressure coefficient

图5给出了5种湍流模型的收敛史对比。由图可以看出，在300步之前，Chien k-ε模型的收敛曲线振荡较大，而其余四种收敛过程相对平稳；而在300～500步之间，S-A，SST k-ω和B-L模型残差下降速度更快；在500～1 000步之间，S-A和SST k-ω模型的残差收敛效果更好，计算稳定性更好，B-L和k-ε-Rt模型的计算稳定性相较于Chien k-ε模型稍好，但相较于S-A模型残差收敛效果较差，而Chien k-ε模型收敛曲线振荡较大，计算稳定性和残差收敛相对较差。

图5 Durham压气机叶栅收敛史Fig.5 Convergence history of the Durham compressor cascade case

3.2 NASA rotor37压气机转子

NASA rotor37轴流压气机转子的进口处于超声速状态，其转速为17188.7r/min，叶顶周向速度为454.14m/s，进口总压为101 325.0Pa，进口总温为288.1K，叶片数为36。计算网格如下图6所示。计算考虑了高度为0.356mm的叶尖间隙。

图6 Rotor37网格Fig.6 Grid used in the Rotor 37 grid

3.2.1 结果及分析

1）网格无关性验证

网格疏密程度是数值模拟中一个很重要的问题，因为不同的网格数量可能会对计算结果和收敛速度造成一定的影响。为了既保证数值计算结果的精度，又能减小计算量、加快收敛速度，因此需要进行网格无关性验证的工作。选择不同的网格数量对NASA rotor37进行数值模拟，通过对计算结果的分析和比较，找到合适的网格数量。

本文采用四种不同的数量网格进行网格无关性研究，分别是方案1网格点的数量为35万、方案2网格点的数量为45万、方案3网格点的数量为55万和方案4网格点的数量为65万，将四种网格分别进行数值计算，采用S-A湍流模型对方程组进行封闭求解，对计算结果进行处理，将不同网格的总体性能与实验数值进行对比。

从图7中可以看出，随着计算网格数量的增加，计算得到的总压比和绝热效率都会有所提高，当网格点的数量大于55万时，可以看到总压比和绝热效率都不会发生明显的变化，因此认为网格的数目达到了网格无关性的要求。同时为了减少计算所需时间，提高效率，因此选择网格数量为55万的方案3来进行后续的数值计算。

图7 网格无关性验证Fig.7 Grid independence verification

2）近最高效率点分析

为了研究湍流模型在NASA rotor37数值模拟中对流场特性的影响，在近最高效率点，从计算结果中分别提取了50%，70%和95%叶高处的S1流面的相对马赫数分布图，并将其与实验数据进行对比，从对流场信息的捕捉能力来分析不同湍流模型的模拟能力。

从图8中可以看出，在50%叶高处，气流以超声速状态进入通道，在到达前缘处的相对马赫数为1.3左右，这与实验数值基本一致，对进口处产生的激波位置和强度的预测与实验数值基本一致，但对激波的宽度计算相较于实验数值偏大。而在通道中间位置，气流由超声速变成了亚声速状态，产生了通道内的激波，B-L和Chien k-ε模型的计算得到的激波位置、强度以及宽度较实验数值偏大，其余湍流模型对激波位置的预测较为准确，S-A模型计算得到的激波强度相较于实验数值偏大，而SST k-ω和k-ε-Rt模型计算得到的激波强度和宽度与实验数值基本一致。当气流流经吸力侧尾部时，产生了气流分离现象，形成了尾迹区域，但各模型的预测结果与实验数值相比偏小，同时对尾缘流动分离现象的捕捉也不够明显。

图8 50%叶高S1流面相对马赫数云图Fig.8 Relative Mach number contour at 50%span

从图9中可以看出，在70%叶高处，各模型对进口处激波位置的预测基本准确，S-A、SST k-ω和k-ε-Rt模型计算的激波宽度和强度与实验数值更为吻合。而对于通道内激波的预测，B-L和Chien k-ε模型的结果与实验数值相差较大，激波位置和强度的预测不够准确，其余三种模型对激波位置的预测与实验数据基本一致，k-ε-Rt和SST k-ω模型计算的激波强度和宽度与实验数值基本一致。

图9 70%叶高S1流面相对马赫数云图Fig.9 Relative Mach number contour at 70%span

从图10中可以看出，在95%叶高处，气流以超声速状态进入进口段，到达叶片前缘处产生了一道激波，SA，SST k-ω和k-ε-Rt模型计算得到的激波宽度和强度与实验数值相对来说更为接近；而对于通道内激波的预测，S-A模型的预测结果与实验数值相差较大，激波位置的预测不准，而其余三种模型对激波位置的预测与实验数据基本一致，同时各湍流模型对于尾迹的预测与实验数值大致相同。

图10 95%叶高S1流面相对马赫数云图Fig.10 Relative Mach number contour at 95%span

为了进一步评估湍流模型的精度，在近最高效率点，对径向参数分布进行对比，如图11～图14所示。从总压比对比图（图11）中可以看出，各湍流模型计算得到总压比分布趋势与实验数值基本一致。在0%～20%叶高之间，B-L模型计算过低预测了总压比，其它四种湍流模型计算出来的数值较实验数值偏大，而Chien kε模型的结果相较于其它模型与实验数值吻合度更高，SST k-ω模型得到的结果误差最大为3.7%；在20%～40%叶高之间B-L模型计算得到的总压比与实验数值几乎完全吻合，而k-ε-Rt模型误差相对较大，误差约为1.8%；在40%～80%，B-L模型得到的结果与实验数值误差最大为1.92%；在80%～100%叶高处，各种模型的预测结果大致相当，但是在97.1%叶高处，所有模型都过高预测了总压比，可能是受到机匣边界层的影响造成的。

图11 总压比的比较Fig.11 Comparison of total pressure ratio

从总温比对比图（图12）中可以看出，在0～20%叶高之间，Chien k-ε和SST k-ω模型计算得到的总温比与实验数值更为接近，其余三种模型计算精度相对较差；在20%～100%叶高之间，k-ε-Rt模型计算的总温比无论是数值上还是分布趋势都与实验数值具有很高的吻合度，其计算精度最高，而在20%～50%叶高之间，Chien kε模型的计算结果与实验数值误差最大为1.27%，在70%～100%叶高之间，B-L模型相较于其余四种模型数值误差更大，约为1.26%。

图12 总温比的比较Fig.12 Comparison of total temperature ratio

从绝热效率对比图（图13）中可以看出，在0～10%叶高之间，所有湍流模型的计算结果都比实验数值偏小，其中k-ε-Rt模型与实验数值相对更吻合，而SST kω模型的预测值误差最大为4%；在10%～30%叶高之间，S-A模型得到的结果与实验数值吻合度更高，而Chien k-ε模型的数值误差最大为2.2%；在30%～60%叶高之间，所有模型得到的结果与实验数值的分布趋势不太一致，而S-A模型计算得到的结果偏差最大为2.83%；在60%～100%叶高之间，S-A模型的计算得到的结果和分布趋势相较于其它模型与实验数值更为接近，SST k-ω模型的预测结果与实验数值偏差最大为6.5%。从轴向绝对速度对比图（图14）中可以看出，所有湍流模型计算得到的进口轴向绝对速度与实验数值都有很高的吻合度，在靠近轮毂，B-L模型的数值偏差较大为4.5%，在靠近机匣处，SST k-ω模型的数值偏差相对较大为3.9%。

图13 绝热效率的对比Fig.13 Comparison of adiabatic efficiency

图14 轴向速度对比Fig.14 Axial velocity comparison

图15为近最高效率计算的收敛史。从图中可以看出，在450步之前，k-ε-Rt模型出现了五次残差较为剧烈的跳跃，而其余四种模型的收敛曲线都较为光滑，收敛速度也基本相同；而在450～1 200步之间，S-A模型的收敛曲线最为平稳，残差下降速度也相对较快，而其它四种模型收敛曲线都有较大的振荡，数值稳定性较差，Chien k-ε残差收敛速度最慢；在1 200～1 900步之间，SST k-ω和k-ε-Rt模型收敛曲线都出现了不同程度的振荡，计算稳定性相对较差，而B-L和S-A模型的计算稳定性和收敛性更好。

图15 Rotor37收敛史Fig.15 Convergence history of the Rotor 37 case

3）变工况性能分析

从总压比特性对比图（图16）中可以看出，在93%～95%阻塞流量之间，B-L模型计算得到的总压比与实验数值最为吻合，而SST k-ω模型的计算结果与实验数值误差最大为1.6%；在95%～100%阻塞流量之间，k-ε-Rt模型的计算结果与实验数值最为吻合，而在接近阻塞流量处Chien k-ε和SST k-ω模型的计算结果与实验数值相差较大，最大数值误差为2.4%。

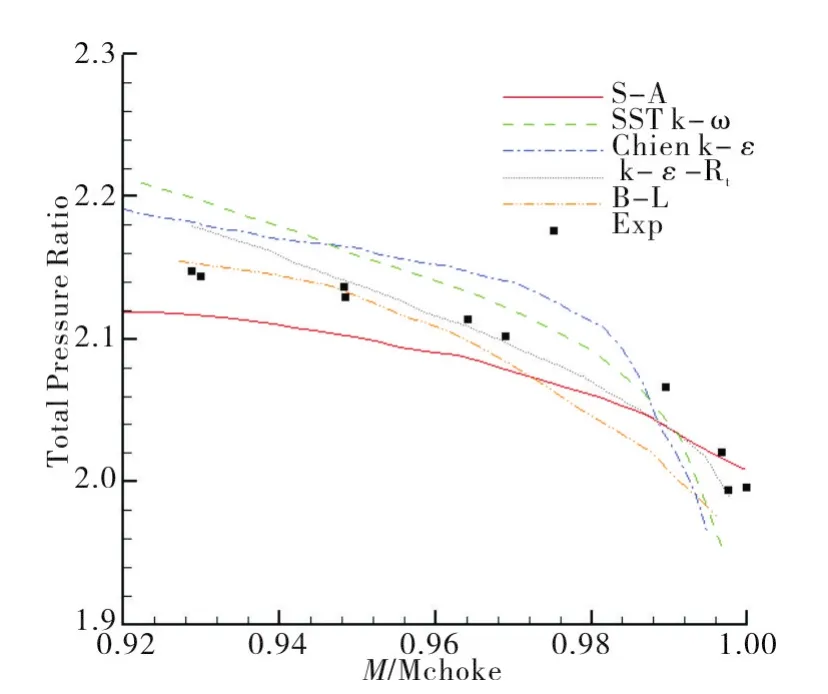
图16 总压比特性对比Fig.16 Comparison of total pressure ratio characteristics

从绝热效率特性对比图（图17）中可以看出，在92%～95%阻塞流量之间，S-A模型计算得到绝热效率与实验数值最为接近，而SST k-ω模型的计算结果与实验数值相比误差最大为2.07%。在95%～99%之间，S-A和k-ε-Rt模型的计算结果相较于其它三种模型与实验数值更为接近，Chien k-ε模型则过高预测了绝热效率，与实验误差最大为1.5%。同时在靠近阻塞流量处，SST k-ω和Chien k-ε模型的计算结果与实验误差最小，而S-A模型在这里的预测结果最差，与实验数值误差最大为1.56%。

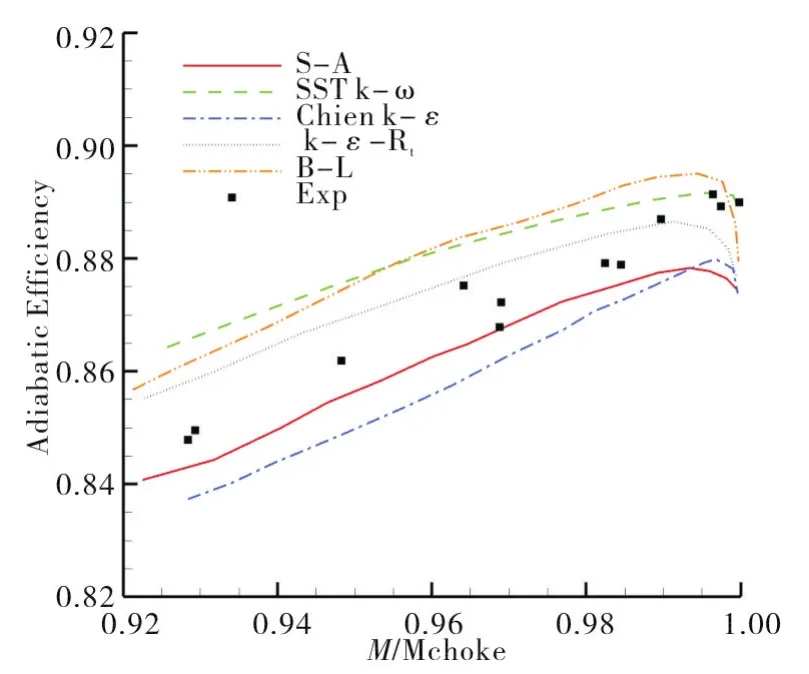
图17 绝热效率特性对比Fig.17 Comparison of adiabatic efficiency characteristics

4 结论

本文以Durham压气机叶栅和NASA rotor37压气机转子为研究对象，将五种不同的湍流模型分别应用于两个算例的数值模拟中，对计算得到的性能参数和流场进行了对比分析，得到以下结论：

1）通过对计算得到的叶片表面压力系数分布、绝热效率特性曲线、总压比特性曲线、总温比、总压比等模拟结果和实验值进行对比分析，Chien k-ε和B-L模型的计算精度最差，k-ε-Rt模型的计算结果与实验数值符合较好，计算精度相对较高，能够应用于低声速叶珊的数值计算。

2）通过对流场的分析对比可以看出，B-L和Chien k-ε模型对流场细节捕捉不够准确，而k-ε-Rt和SST kω模型对于激波的预测更为准确，能够较好地反映真实的流动情况，可以应用于跨声速轴流压气机的数值模拟，但是靠近尾缘处的气流分离现象的模拟结果不够明显。

3）从各湍流模型的计算收敛史可以看出，Chien k-ε模型的收敛性最差，k-ε-Rt模型的计算稳定性较差，而S-A模型的计算稳定性以及残差收敛性都表现得更好。