自由段弹道目标跟踪算法在工程中的应用

李启飞，吴 芳，范赵鹏

（1.91550部队，辽宁大连116000；2.海军航空大学，山东烟台264001；3.91001部队，北京100000）

弹道目标跟踪是弹道防御系统中极其重要的任务之一[1-3]，跟踪的精度将直接影响弹道预报初值点的精度，会影响弹道的拦截[4-5]。因此，对目标精确跟踪是当前雷达技术领域的一个热点和难点。与助推段和再入段相比，弹道目标自由段防御具有更加重要的地位[5]，其优点主要有：防御面积大，可以节省大量的兵力；拦截时间长，可实施多次拦截。但在大气层以外飞行，受地球引力的作用，弹道目标的自由防御段难以进行有效的机动。且弹道相对单一，弹头从弹体分离后常呈现加速飞行的特点[6-7]。因此，弹道目标自由段防御的军事研究价值显得尤为重要。

本文主要研究自由段的弹道目标跟踪问题，在这个阶段，目标在大气层外运动，空气阻力和其他摄动力可以忽略，仅考虑地球引力作用[8]。通常来说目标飞行平稳，仅有某些先进的目标可以进行些小的机动[9-10]。弹道目标的跟踪是一个连续的非线性滤波过程，其运动状态非线性、量测非线性。传统的弹道目标跟踪方法，利用扩展卡尔曼滤波器（EKF）进行非线性滤波[9]，但是本文选取自适应跟踪模型[11-13]，其可以将机动加速度转化为一个不相关的白噪声。此时，用卡尔曼滤波（KF）即可获得较好的跟踪效果，而无须采用扩展卡尔曼再次对目标量测模型进行线性化，从而简化算法，减少运算时间。为了验证算法性能，本文中采用Singer和当前统计（CS）2种自适应跟踪模型结合卡尔曼滤波进行目标跟踪，与扩展卡尔曼滤波进行了对比验证。

1 基于Singer-KF的跟踪滤波算法

为了更好地对弹道目标进行跟踪，这里采用比较精确的包含地球形状动力学系数J2项的标准椭球地球重力模型[14-16]，并将其和Singer算法相结合解决弹道目标跟踪问题。

在雷达站ENU坐标系下的目标动力学模型为：

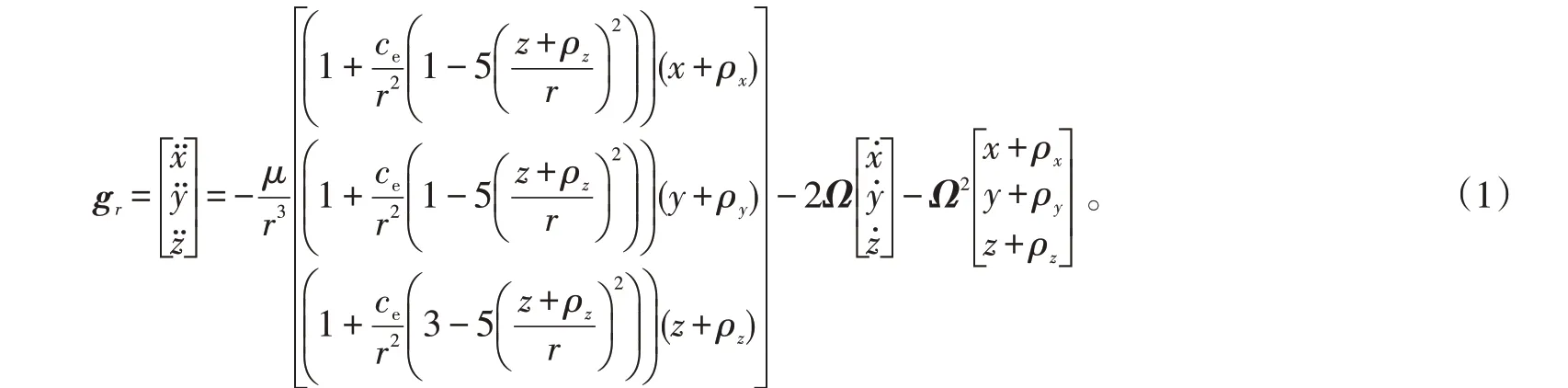
设B 为雷达站大地纬度，φ 为雷达站地心纬度，则地心纬度与大地纬度间的转换关系式为：

式（3）中：a、b 分别为地球椭圆长半轴、短半轴，且a=6 378 137 m，b=6 356 755 m。

令θ=B-φ，则

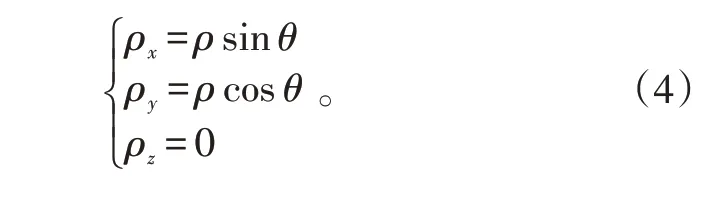
式（4）中，ρ=re+z，z 为ENU坐标系下的z 轴数据，而

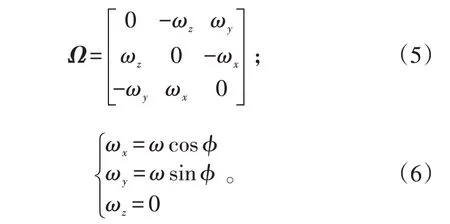
这 里 ， ω 为 地 球 自 转 角 速 度 ，且ω=7.27×10-5rad/s。

弹道目标的状态方程为：

且

式（8）、（9）中：0 为3×3的全零矩阵，T 为采样间隔，α是机动时间常数的倒数，即机动频率，而

可得状态的一步预测为：

状态预测值的估计误差：

协方差的一步预测：

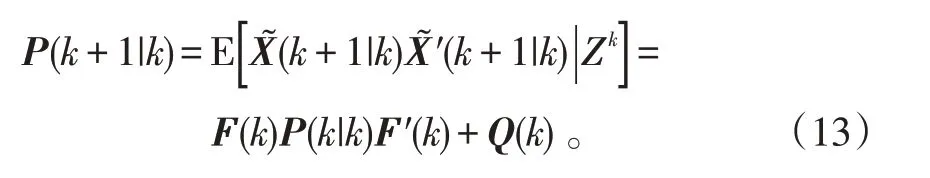
式（13）中，过程噪声协方差矩阵为：

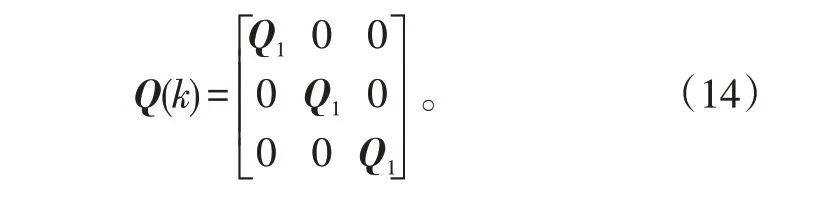
式（14）中：

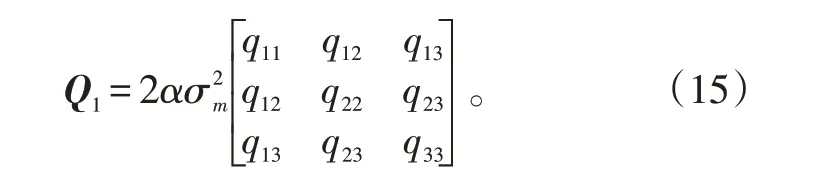
式（15）中：σ2

m是目标的加速度方差。而

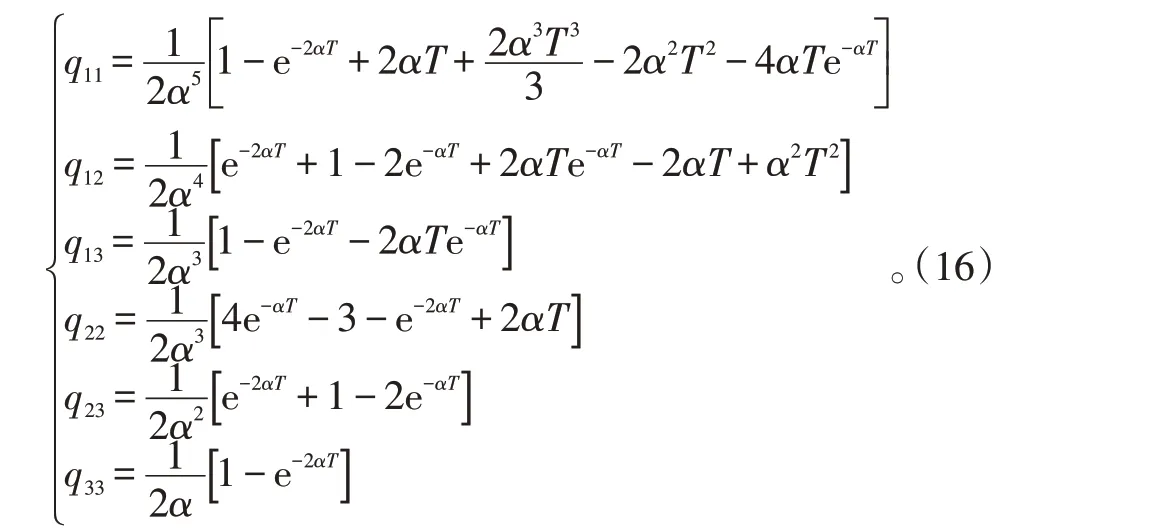
对于机动加速度方差σ2

m，可由下式获得：

式（17）中：pM为目标机动加速度等于极大值aM或极小值-aM的概率p0为非机动概率（机动加速度等于0的概率），机动加速度在区间[ ]-aM,aM上近似服从均匀分布。

量测值的进一步预测

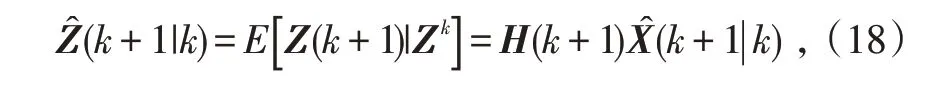
式中，量测矩阵H(k+1)为：

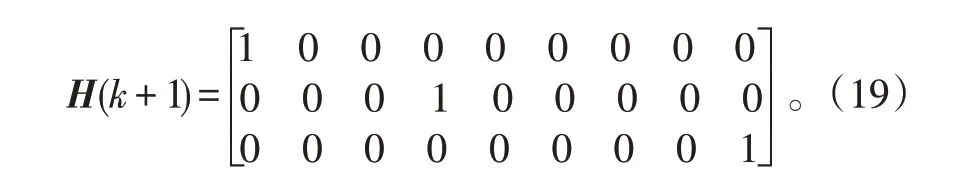
新息协方差为：

式中，R(k+1)为ENU 直角坐标系下的转换量测噪声协方差矩阵。

增益为：

状态更新方程为：

式（23）中：I 为9×9的单位阵。

须要强调的是，运动模型是在ENU 直角坐标系下，量测模型是在雷达站极坐标下，跟踪滤波过程需要进行坐标系间的转换[8]。

2 基于CS-KF的跟踪滤波算法

该算法采用修正瑞利分布来描述机动加速度的统计特性，所假设的分布具有分布随均值变化而变化，方差由均值决定的优点[17]。因此，算法在估计目标状态的同时，还可辨识出机动加速度均值，从而实时地修正加速度分布，并通过方差反馈到下一时刻的滤波增益中，实现了闭环自适应跟踪。

设目标运动状态方程为：

式（24）中，F(k)如式（8）所述，G(k)为输入控制矩阵，即

该算法的一步预测方程为：

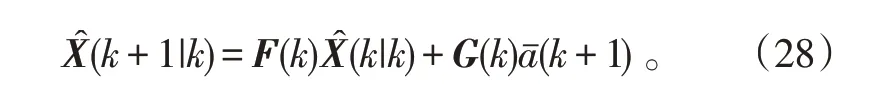
其余跟踪步骤同第1节。

3 自适应模型下EKF滤波算法

跟前文一样，目标运动状态可选择用Singer 或者CS模型，这里选择用EKF进行滤波。

量测方程为：

式（29）中，

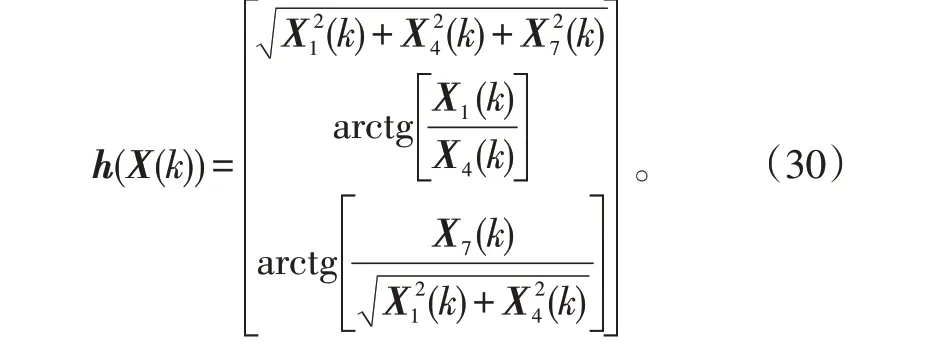
V(k)是离散时间白噪声序列，且

与其相伴的协方差（近似的均方误差）为：

其中，雅可比矩阵[18]为：

增益为：

状态更新方程为：

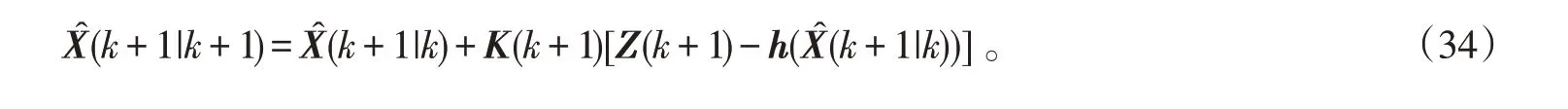
协方差更新方程为：

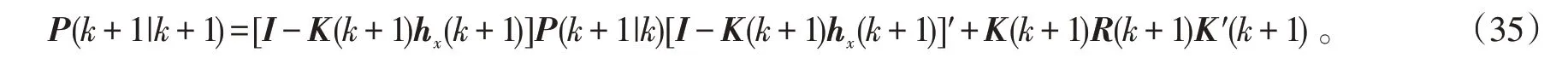
4 仿真及结果分析

设关机点目标的经度为0°，纬度为0°，高度为80 km，在地心地固坐标系下三轴上的速度分量均为3 km/s。雷达站经纬度为东经1.5°，北纬9.5°，大地高程0 m，雷达探测频率1 Hz，采样时间860 s，雷达的测距误差均方差为6 m，方位和俯仰测角误差均方差为0.001 4 rad，通过给定的误差均方差，基于高斯分布模型随机产生各观测时刻距离、方位角误差数据，并叠加于仿真弹道，生成的雷达对弹头的测量数据，如图1 所示。Singer 模型中选取参数α=1 000 ，aM=100，pM=0.6，p0=0.2，ENU 坐标系下分别采用Singer模型结合卡尔曼滤波和扩展卡尔曼滤波对目标进行跟踪，为更清晰显示滤波结果，选取其中401～450 s 测量时间段内的50 个跟踪步数进行放大显示，如图2 所示。CS 模型中选取参数α=0.1，aM=100，ENU坐标系下采用CS模型结合卡尔曼滤波和扩展卡尔曼滤波的跟踪结果（401～450 s）如图3所示。

图1 雷达对弹头的测量数据图Fig.1 Radar measurement data map of warhead

图2 Singer-KF与Singer-EKF的放大滤波图Fig.2 Enlarged filter map of Singer-KF and Singer-EKF

图3 CS-KF与CS-EKF的放大滤波图Fig.3 Enlarged filter diagram of CS-KF and CS-EKF

由图2、3可以看出，2种自适应模型与两种滤波算法相结合后都能取得较好的滤波效果。

为了分析比较2 种滤波方式的滤波精度，本文选取位置均方根误差（RMSE）作为衡量参数，图4 显示的是50个跟踪步骤中Singer-KF与Singer-EKF的位置均方根误差的对比，图5 显示的是50 个跟踪步骤中CS-KF与CS-EKF位置均方根误差的对比。仿真结果表明，与自适应算法结合后，卡尔曼滤波精度与扩展卡尔曼滤波精度基本一致。

图4 Singer-KF与Singer-EKF的RMSE放大图Fig.4 RMSE enlarged drawing of Singer-KF and Singer-EKF

图5 CS-KF与CS-EKF的RMSE的放大图Fig.5 Enlarged RMSE of CS-KF and CS-EKF

表1 2种算法下的单步耗时比较Tab.1 Comparision of single step time between the two algorithms

4 结论

本文基于工程需要研究了自由段弹道目标的跟踪问题。通过仿真实验验证，KF、EKF 2 种滤波方式分别与自适应跟踪模型相结合后，KF 滤波可以达到与EKF 滤波几乎相同的滤波效果，但其算法简单、运算时间短，可以较好满足自由段弹道目标跟踪的工程需求。另外，本文采用的是仿真测量数据，数据测量较为理想，在实际弹道跟踪问题的解决中还需要针对部分时刻测量数据的缺失以及虚假干扰数据信息进行特殊算法处理，从而更好地解决自由段弹道目标的跟踪问题。