基于计算机仿真技术的混合介质电特性研究

郭 晨，马念茹

(长安大学 信息工程学院，陕西 西安 710064)

0 引 言

目前计算机仿真技术已经广泛用于生活的各个方面，尤其是在科研方面更是发挥了极大的优势。通过对实际问题建立系统的模型，通过高效的数值计算工具和算法对模型进行计算，可以定量分析并准确快速解决工程与实际生活中的复杂问题。高效、准确、受环境条件的约束较少、设备简单的优点使得计算机仿真技术已经成为分析设计实际问题的主流手段。

用计算机仿真技术建模计算混合介质等效介电常数来研究混合介质电特性[1-4]时，前人大多只对混合介质的几何结构、各组分的比例进行建模[5-6]。研究混合介质的几何结构和组分的不同比例对等效介电常数的影响，混合公式与理论模型很少考虑各相成分几何分布对混合介质电特性的影响。而几何分布对混合介质电特性至关重要。文中在用计算机仿真技术建模时考虑了各相成分的不同几何分布，对不同几何分布进行仿真建模。并根据仿真计算的结果对混合公式进行修正。在混合公式里面加入几何修正因子。通过MATLAB编程将几何修正因子确定为孔隙度的六次多项式。将修正后的理论公式与计算机仿真结果进行对比，修正后的理论公式在不同的几何分布模型上都适用，为储层岩石物理特性分析及不同组分含量的预测提供理论依据与仿真基础。

1 仿真技术

1.1 COMSOL Multiphysics

在仿真研究中，文中使用COMSOL Multiphysics高级数值仿真软件来研究三相混合介质的有效电性质[7-9]。COMSOL Multiphysics采用有限元算法，通过求解偏微分方程来仿真物理现象。

选取物理场为静电场，对三维空间进行建模[10-11]，电压设置100 V，选取建模完成后为混合介质添加材料，混合介质介电常数分布设置为固体颗粒(～4)，润湿相(～80)，非润湿相(～2)。网格选取自由剖分四面体，并对网格参数重新进行设置，在稳态下进行研究。在求解微分方程时，选择电场通量与电场强度，COMSOL Multiphysics直接计算出结果。作为一款强大的计算机仿真软件，COMSOL在各领域的计算与模拟中都表现出极大的优势。具体仿真流程如图1所示。

图1 COMSOL Multiphysics具体仿真过程

1.2 最小二乘法曲线拟合

最小二乘法最初是由高斯提出的，为解决数据最佳匹配函数问题。最小二乘法原理即确定使每次测量误差的平方和最小的被测量真值的最佳值。具体原理如下：给定一组测量数据集合{(xi,yi),i=1,2,…,n}，设该组数据集拟合函数为φ(x)。拟合函数应尽可能多地反映出绝大部分数据的变化规律，但不要求反映全部数据。因此拟合函数在xi处与实际测量值存在一定误差，误差用Ei表示。

Ei=φ(xi)-yi,i=1,2,…,n

(1)

为了使拟合曲线更好地满足数据的变化规律E2最小。

E2=∑(φ(xi)-yi)2

(2)

通过MATLAB编程利用最小二乘法[12-13]，使理论公式与仿真数值解平方差最小，并确定修正几何因子关于孔隙度的函数，通过其他分布验证几何修正因子的正确性。

2 几何分布模型设计

仿真建模了两种混合介质结构：(1)水(W)包裹着石油(N)，固体颗粒(S)分布在周围(SWN模型)；(2)水包裹着岩石颗粒，石油分布在周围(NWS模型)。分布模型如图2所示。最外面的骨架记为m,外面的复合球记为s,最里面的球记为c。几何分布模型[14]主要设置了四种：简单分布(SC)、体心分布(BC)、面心分布(FC)、随机分布(RD)。

图2 分布模型

3 修正公式

3.1 几何修正因子

仿真计算结束后，得到COMSOL Multiphysics 的仿真结果，并与经典混合公式Lorentz-Lorenz-Clausius-Mossitt(LLCM)公式做对比。发现在孔隙度增大到一定程度后，解析公式与仿真数值结果不吻合，由此提出对解析公式进行修正。图3为COMSOL数值解(孔隙度从0.03～0.96)，未修正LLCM解析解，修正后LLCM公式解析解的对比情况。

图3 LLCM公式、修正后的LLCM公式的计算结果及数值解对比

Sihvola[15]曾提出可以给LLCM公式添加修正参数μ。文中根据混合介质的不同分布确定修正参数μ，把μ称为几何修正因子。

3.2 最小二乘法修正公式

由于SC分布孔隙度变化范围大，在MATLAB编程利用SC分布的仿真数据集(等效介电常数，孔隙度)。设置几何修正因子μ变化范围0.01～0.1，将SC分布的仿真结果带入到修正的LLCM公式。根据最小二乘法原则即修正的LLCM公式计算结果与仿真结果平方差最小原则，选取出最优的几何修正因子μ。利用曲线拟合将几何修正因子μ确定为关于孔隙度的六次多项式。通过其他分布验证修正公式的正确性。修正后的LLCM公式如下：

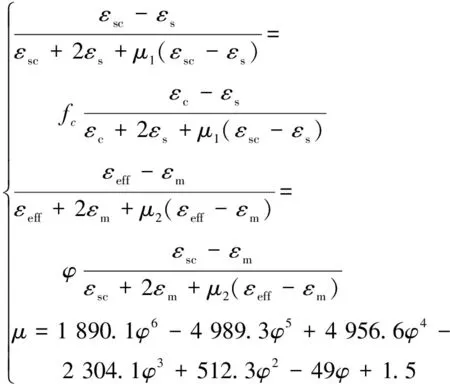
(3)

(4)

以NWS结构的SC分布为例，图4为SWN与NWS两种结构下μ2与孔隙度的关系。

图4 SC分布下，SWN结构与NWS结构μ2与孔隙度的关系

3.3 仿真数值解与修正后公式对比

图5为SWN结构和NWS结构SC、BC、FC、Rand-om四种分布下修正后的LLCM公式与仿真数值解对比。

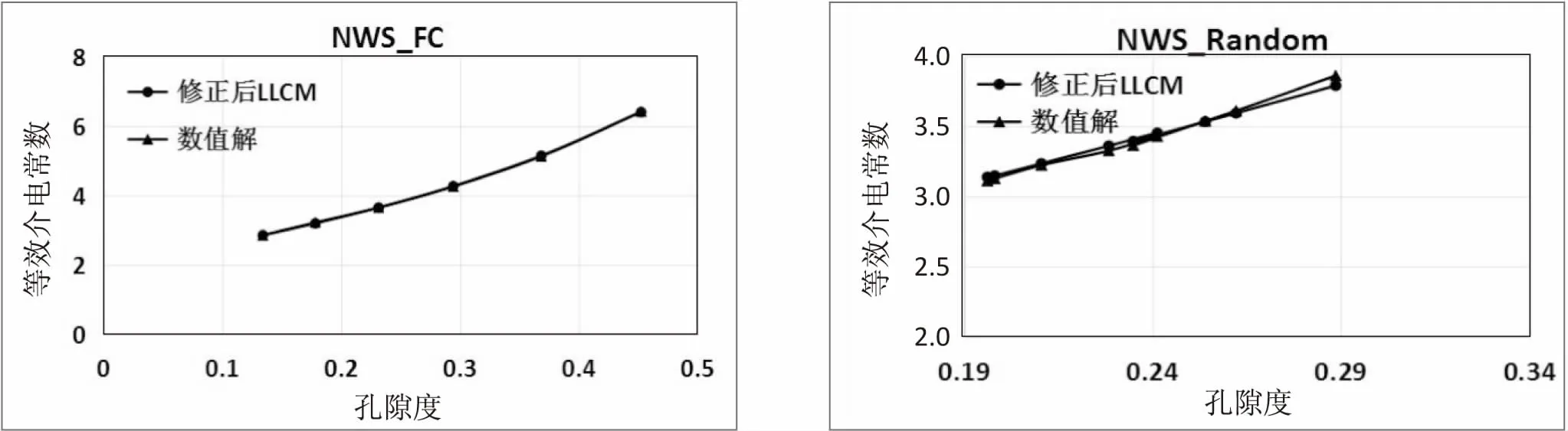
图5 SWN结构和NWS结构SC、BC、FC、Random四种分布下修正后的LLCM公式与仿真数值解对比

4 结束语

利用计算机仿真的方法研究了各相几何分布对混合介质电特性的影响，构建了四种几何分布。通过COMSOL Multiphysics计算不同几何分布下混合介质等效介电常数。根据仿真计算结果和最小二乘法确定理论公式的几何修正因子，对理论公式进行修正。结果验证了修正方法的正确性。通过该仿真研究为混合介质电特性预测奠定仿真基础，修正后的理论公式可以直接用于计算不同几何分布下混合介质等效介电常数，为仿真计算结果提供充分的理论参照。