数形结合思想演绎精彩课堂

孙丽华

[摘要]“分数乘分数”是一节计算课，刘万元老师充分运用“数形结合”思想，让学生在有效情境中激发兴趣、在画图操作中感悟算理、在质疑探究中明确算法、在巩固练习中拓展思维、在回顾总结中提升思想，诠释了“以生为本”的教学理念，实～L-J"完美元瑕的精彩演绎。

[关键词]兴趣;算理;算法;思维

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）17-0054-02

山东省刘万元老师执教的“分数乘分数”把一节枯燥的计算课演绎得十分精彩，我深深地被刘老师精湛的教学艺术、高超的教学智慧所折服，而这都归功于“数形结合”思想。

一、在有效情境中激发兴趣

[课堂回放1]

师：后面的2个算式与第1个算式有什么不同？

生：第1个算式是分数乘以整数，后面的2个算式都是分数乘以分数。

师：是的，今天我们就一起来学习分数乘分数。

通过创设有效的教学情境，引发学生的有意注意，培养学生发现问题、提出问题的能力，并通过观察比较，提升学生参与的活跃度，使学生的思维一直跟着教师走，从而自然地引入课题。

二、在画图操作中感悟算理

[课堂回放2]

师：对于这个新问题，你们准备用什么方法来进行研究呢？

生1：可以用画图的方法。以前我们研究分数时就用过画图的方法。

师：非常好。听了这两位同学的介绍后，谁能简单概括一下画图的过程？

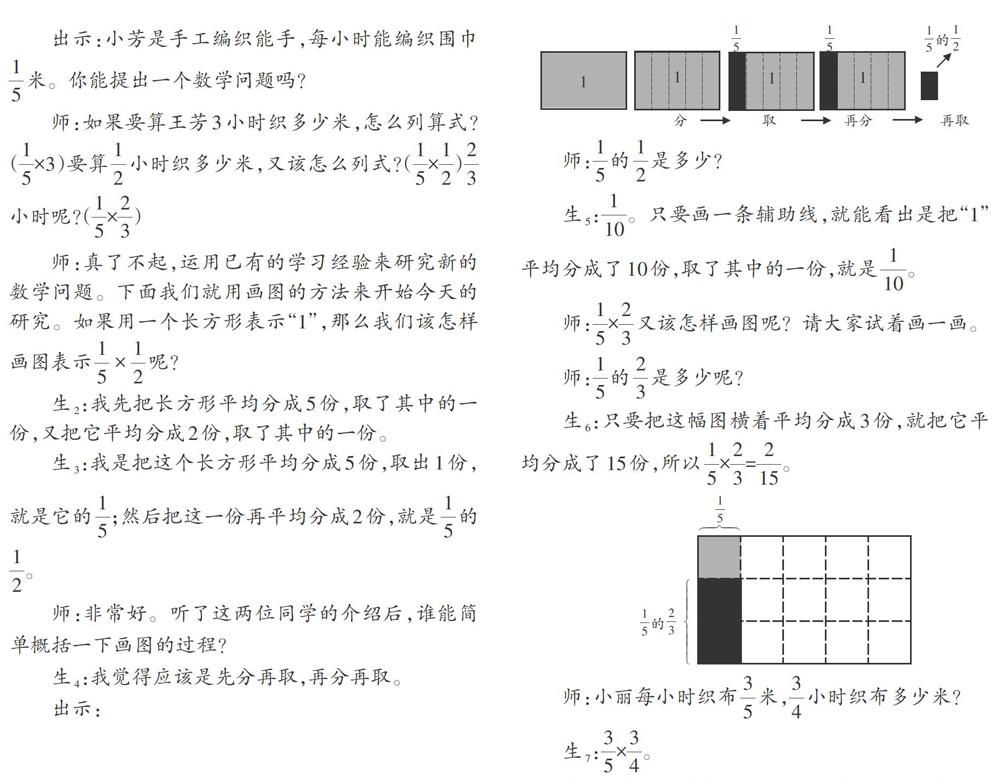
生4：我觉得应该是先分再取，再分再取。

出示：

生10：一个数乘分数实际上求的就是这个数的几分之几是多少。

小学生以直观形象思维为主。刘老师能够利用学生的已有经验，引导学生通过画图来研究，使学生在操作中积累了数学活动经验，并通过数形结合，直观感知“分一取一再分一再取”的过程，感悟算理，体验整个建模的过程，为进一步探究算法积累丰富的表象。

三、在质疑探究中明确算法

[课堂回放3]

师：分母相乘表示什么？分子相乘表示什么？

生6：分母相乘表示一共平均分成了多少份，分子相乘表示取了多少份。

师：以后遇到分数乘分数的问题，该怎么算呢？

生3：求的是其中的1份。

師：约分不仅仅是为了计算简便，背后还隐藏着它的道理。

刘老师设计的课堂练习充分利用了学生的已有经验，把解决问题与约分算理紧密联系起来，不仅仅关注学生数学知识和技能的掌握，更将算理、算法以及实际应用完美结合，培养学生的探究意识和创新能力。

五、在回顾总结中提升思想

[课堂回放5]

师：这节课，我们收获了什么知识？

师：回顾刚才的学习过程，我们经历了哪几个步骤呢？

生1：先举例，根据这些例子又进行猜想，然后验证，最后得出了结论。

师：还有什么收获要跟大家分享吗？

生2：可以用画图来研究分数乘分数。

师：是的，研究数的问题，可以请图形来帮忙，数学上把这种研究问题的方法叫作数形结合。

回顾学习过程是很重要的一个环节，刘老师在结课前引导学生梳理学习内容、建构数学模型、反思学习过程，结合板书、多媒体课件，将关键词“举例、猜想、验证、结论”依次呈现，提炼出数形结合的数学思想方法。

纵观本节课，无论是在理解意义、探究算理的过程中，还是在巩固练习、课堂总结环节，刘老师很好地运用了“数形结合”的思想，诠释了“以生为本”的教学理念。

（责编金铃）