基于改进A*算法的无人车路径规划研究

李琼琼，施杨洋，布升强，杨家富

(南京林业大学机械电子工程学院，江苏 南京 210037)

随着汽车保有量的不断增加，交通事故发生的概率也越来越大，汽车安全已成为全社会关注的焦点问题。无人驾驶技术在降低道路交通事故发生率方面有着重要的研究意义和价值。随着人工智能的应用和发展，无人驾驶汽车越来越受到关注，路径规划问题也已成为当下研究的热点[1]。无人车路径规划是指在有障碍物的环境中，快速规划出一条连接起始点与目标点的可行路径[2]。近年来关于无人车路径规划问题，很多学者提出了各种应用于不同场景的路径规划算法。主要有基于地图搜索的概率路图法[3]和快速随机拓展树法[4]，基于节点搜索的A*和D*算法[5-6]，基于启发搜索的粒子群算法和蚁群算法等[7-8]。

对于静态环境，A*算法是搜索路径最有效的方法之一，因此被广泛应用在路径规划仿真实验中[9]。但由于其本身搜索原理的限制，A*算法规划路径效率虽高但转折点较多，考虑到无人车的具体尺寸和行驶时的环境状况，转折点较多不利于无人车的行驶。Botea A 等[10]提出了HPA*算法，通过减小搜索空间来提高搜索速度，有效地提高了寻路效率，但其往往得不到最优路径，还需要进一步搜索来实现对路径的优化，增加了计算量；王红卫等[11]提出了一种平滑方法，解决了无人车路径规划转折点多的问题，但没有缩短路径的长度；辛煜等[12]提出了一种改进A*的算法，对栅格地图中的栅格进行线性插值，解决了传统A*算法平滑性较差的问题，但其增加了可搜索邻域和搜索方向，导致搜索的时间变长。

基于以上各方法的特点，本文提出一种改进的A*算法，将一个搜索优先级信息引入启发函数中，使A*算法在进行路径规划时优先搜索初始点和目标点对角连线区域，缩短了路径长度和搜索时间。

1 环境建模及地图预处理

在无人车的路径规划中，需要将各传感器采集到的环境信息进行融合，建立一个能表示周围环境的地图模型。目前环境建模方面应用最广泛的方法之一是栅格法，其具有简单、易于实现的特点。

本文采用21×21栅格组成的地图来表示无人车周围的环境信息，如图1所示。栅格法将无人车行驶环境用一系列具有相同尺寸的栅格表示，并根据环境信息将栅格地图分为行驶区域和障碍物区域。其中行驶区域为白色栅格，障碍物区域为黑色栅格。地图四周边界处都设置为障碍物，防止初始点和目标点设置在地图外侧。若输入的初始点或目标点的坐标与某障碍物坐标重合，则地图默认把此障碍物删除。

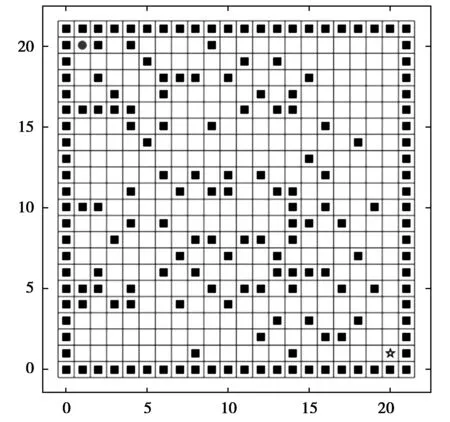
图1 栅格地图

为便于研究和进行仿真实验，本文做出以下合理假设：

(1)假设地图和障碍物边界都是在考虑无人车安全距离的情况下建立，因此可以将无人车视为一个质点，且只能在网格范围内移动。

(2)在没有边界和障碍物的情况下，无人车可以向周围8个方向的栅格移动，并且不考虑自身外型的影响。

(3)在无人车寻径过程中，周围环境保持不变。

2 传统A*寻路算法

A*算法是一种应用于静态全局路径规划的搜索算法，其关键在于评价函数的选取[13]。从初始点开始，根据启发函数搜索与初始点相邻的节点，通过代价函数来选取最优的一个相邻节点作为当前节点继续前进搜索，直至搜索到目标点为止，最后由目标点回溯到初始点连接形成一条全局规划路径。其代价估计函数为：

f(x，y)=g(x，y)+h(x，y)

(1)

式中：f(x，y)为起始点到目标点的估价函数；g(x，y)为从起始点到当前节点的实际代价值；h(x，y)为启发函数，表示当前节点到目标点的代价估计值。若h(x，y)=0，即启发函数为零，估价函数完全由g(x，y)决定，搜索效率降低，A*算法退化为Dijkstra算法；若g(x，y)=0，则估价函数完全由启发函数h(x，y)决定，A*算法演变为宽度优先搜索算法。A*算法是否高效取决于启发函数h(x，y)。h(x，y)中包含的启发式信息越多，搜索路径的效率越高；h(x，y)中包含的启发式信息越少，规划出来的路径与最优路径相差就越大。A*算法中有Open与Close列表，其中有待搜索的可行相邻节点存放在Open列表中，已搜索过的节点保存在Close列表中。传统A*算法流程图如图2所示。

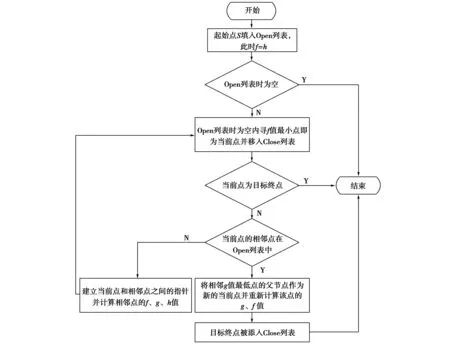
图2 传统A*算法流程图

3 改进的A*算法

启发函数的选取对于整个A*算法至关重要，若想寻得最优路径，需要保证始终小于当前节点到目标点的实际距离。传统A*算法通常采用曼哈顿距离和欧氏距离作为启发函数。若无人车可以朝任意方向移动，常采用欧氏距离来表示对应的启发函数：

(2)

但本文中以栅格作为地图环境，地图中存在障碍物，无人车不能全向移动，且采用欧式距离的搜索速度比曼哈顿慢，因此本文选用曼哈顿距离作为启发函数：

h(x，y)=B×(|xi-xg|+|yi-yg|)

(3)

式(2)、式(3)中B为每个相邻单位节点之间的路径代价，无人车当前的位置为(xi，yi)，目标点位置为(xg，yg)。

起始点和目标点的对角连线附近连线区域为最优路径大概率出现的地方，可视为优先搜索区域。最优路径的出现概率随着优先搜索区域向两侧延伸而减小。基于此理论，本文提出一种新的启发函数，具体为在原有的启发函数h(x，y)里引入一个搜索优先级启发式信息η(i，j)=1/d(i，j)，其中：

(4)

h′(x，y)=B×(|xi-xg|+|yi-yg|)×η(i，j)

(5)

式(4)中，(xi，yi)表示当前节点的坐标位置，(xs，ys)表示起始点，(xo，yo)表示原点位置，(xn，yn)表示栅格地图顶点坐标，mid表示地图划分的分割线。基于地图位置信息划分过的启发式函数，划分出核心区域和非核心区域。在无人车搜索路径过程中，从起始点开始，根据目标点的位置，优先搜索起始点和目标点的对角连线附近区域，若该区域内有障碍物，则搜索区域逐渐向两侧偏离。搜索优先级启发式信息量，沿着初始点与目标点的连线向两侧递减。

4 仿真实验与结果分析

本文基于MATLAB 2018b软件来验证改进A*算法的有效性。首先建立一个21×21的栅格地图，为便于仿真，将无人车视为一个质点。初始点设为(1，20)，目标点设置为(20，1)。障碍物和边界位置固定，传统A*算法仿真实验如图3所示，改进后的A*算法仿真实验如图4所示，两种算法仿真实验结果对比见表1。其中，“★”表示Close节点，“+”为Open节点，连线为规划出的路径；保证初始点和目标点分别为(1，20)和(20，1)，保持地图环境不变，对改进前后的A*算法分别进行25次仿真实验，两者时间对比结果如图5所示；改变起始点和目标点，保持地图环境不变，进行10次仿真实验，得到的实验数据见表2。

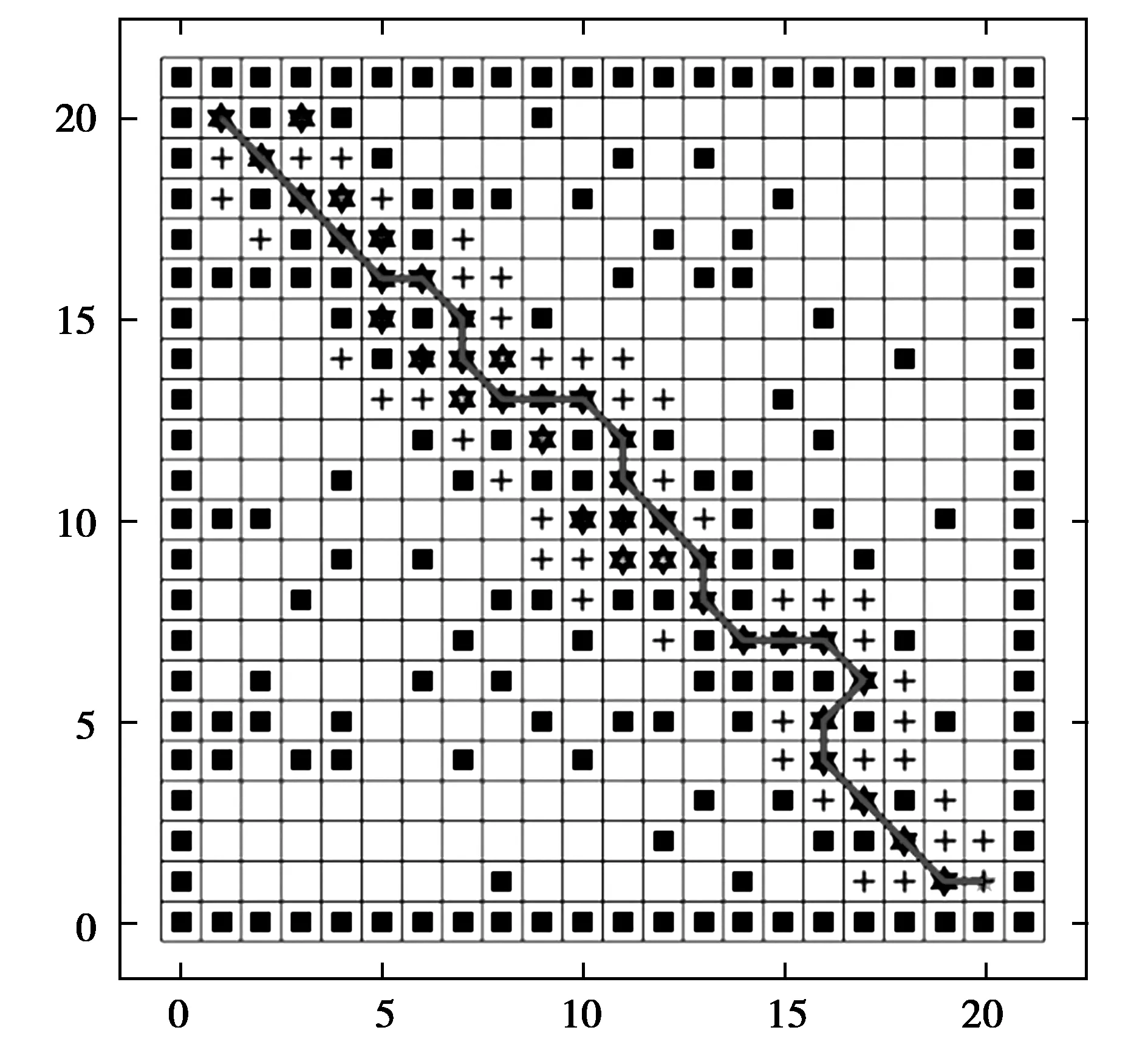
图3 传统A*算法仿真实验

由图3和图4可知，相对于传统A*算法，启发函数引入优先级启发式信息，使A*算法搜索路径时优先搜索初始点和目标点连线区域，减少了A*算法的随机性。由表1可知，改进A*算法仿真实验所得到的路径轨迹转折点较少且平均转折角度减小，路径轨迹更加平滑，缩短了路径的长度和路径规划所需的时间，顺利到达了目标位置，提高了搜索效率，实现了路径优化目标。

表1 两种算法仿真实验结果

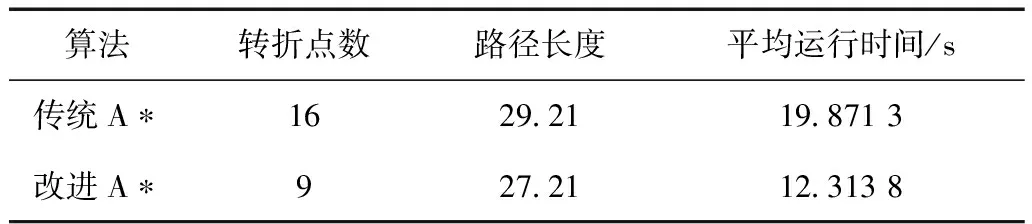
算法转折点数路径长度平均运行时间/s传统A∗1629.2119.871 3改进A∗927.2112.313 8

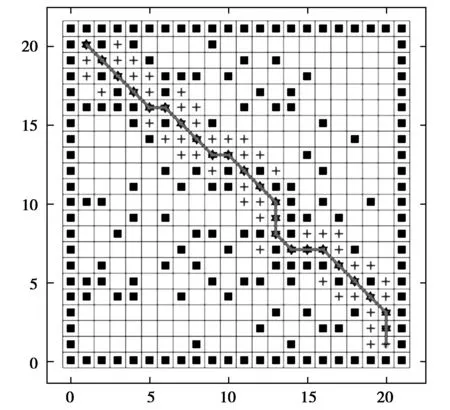
图4 改进A*算法仿真实验

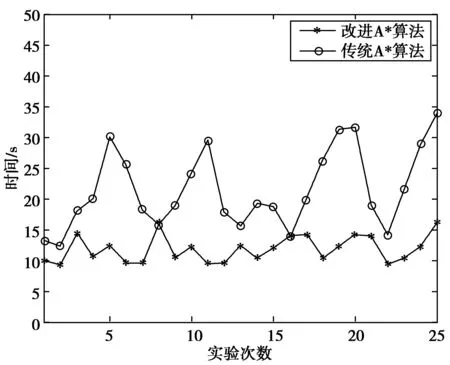
图5 时间对比

表2 两种算法仿真实验数据

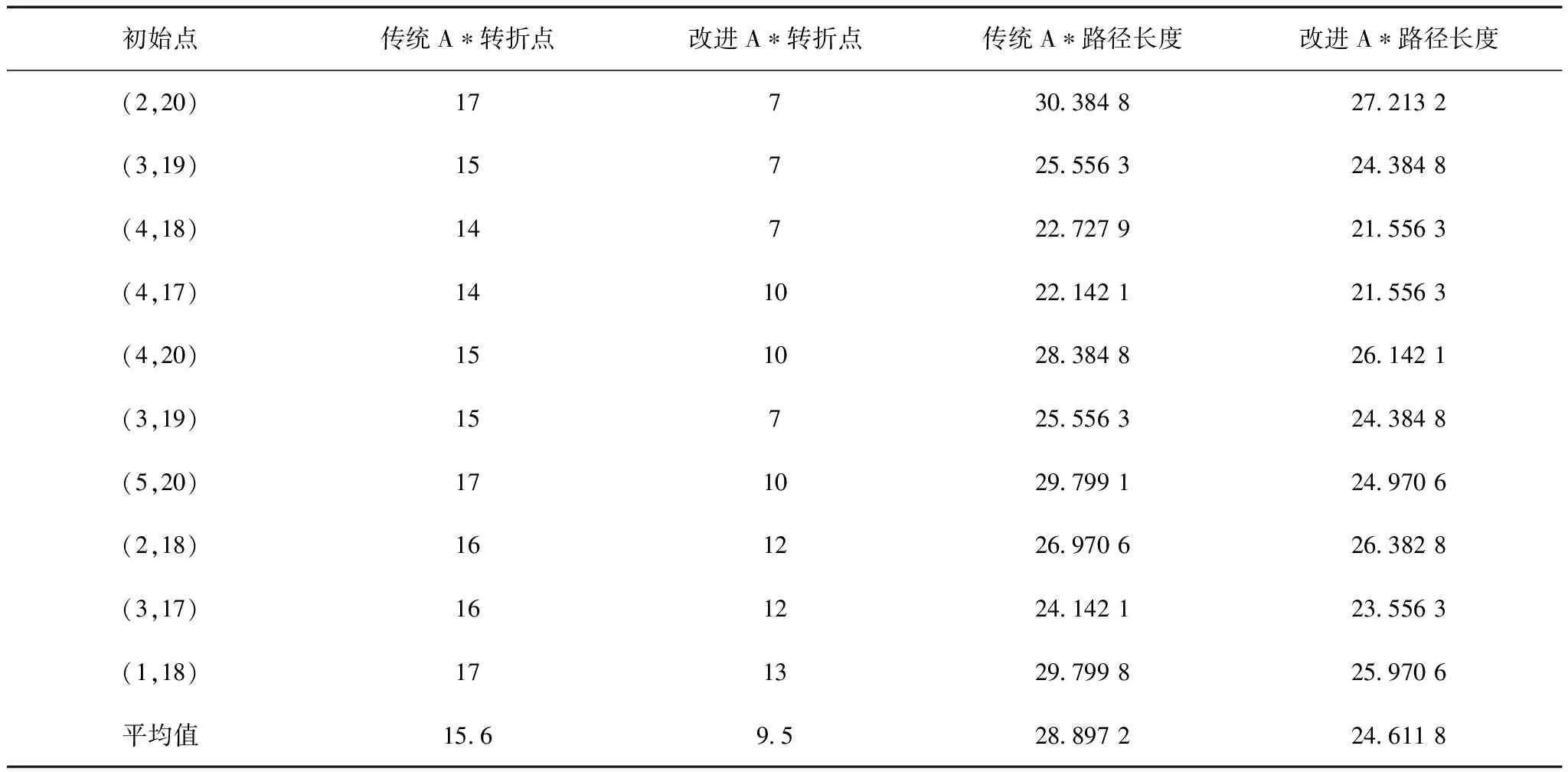
初始点传统A∗转折点改进A∗转折点传统A∗路径长度改进A∗路径长度(2,20)17730.384 827.213 2(3,19)15725.556 324.384 8(4,18)14722.727 921.556 3(4,17)141022.142 121.556 3(4,20)151028.384 826.142 1(3,19)15725.556 324.384 8(5,20)171029.799 124.970 6(2,18)161226.970 626.382 8(3,17)161224.142 123.556 3(1,18)171329.799 825.970 6平均值15.69.528.897 224.611 8

注：令每一个目标点的横坐标和纵坐标分别与初始点的纵坐标和横坐标相同

由表2可知，多次实验中，改进A*算法的转折点个数均少于传统A*算法，实现了路径平滑。此外，基于改进A*算法得到的路径长度均小于传统A*算法。实验表明改进的A*算法在路径平滑、缩短路径长度、提高搜索效率方面有显著的效果。

5 结束语

针对无人车路径规划问题，以传统A*算法为基础，在启发函数里引入新的搜索优先级信息，在路径搜索过程中，以起始点和目标点的对角线为基准，优先搜索起始点和目标点的对角连线附近区域，减少了A*算法寻径时的随机性，提高了搜索效率，改善了传统A*算法耗时长、转折点多和路径不平滑等不足。本文设计的改进A*算法，对路径的转折角度和长度的优化效果不明显，需要进一步的研究