基于多层感知机的木材颜色分类

庄子龙，刘 英，沈鹭翔，丁奉龙，王争光

(南京林业大学机械电子工程学院，江苏 南京 210037)

1 木材颜色图像处理的国内外相关研究

木材具有很多优良的性质，如调湿特性、隔声吸音特性、对热和电的绝缘性等，使得木材在家具行业中有着广泛的运用。木材表面的重要参数有木材的色彩和纹理，木材的颜色特征可以很好地描述木材的整体外观特征，作为木材种类、等级分选的重要依据。目前对木材颜色进行分类主要靠人工进行，这种分选工作效率不高，需要工人丰富的经验，作业效率也容易受到工人状态的影响，而通过图像识别进行木材的颜色分选可以大大提高木材颜色分选的效率和准确性，满足木材加工企业生产的需要。

国内外利用机器视觉对木材进行评估的研究很多。Yusof等[1]提出了Gabor滤波器从单个图像生成多个处理后的图像，以便通过神经网络提取和训练更多特征。Pramunendar等[2]使用自调整MLP分类器(AutoMLP)和支持向量机(SVM)进行椰子木质量分类的实验工作。Francesco Bianconi等[3]通过实验研究和比较各种颜色描述符、颜色空间的性能发现简单而紧凑的颜色描述符与更复杂的特征一样准确。Yadav等提出了一种基于纹理特征的硬木树种分类方法。Yadav等[4]集成了局部二值模式(local binary pattern，LBP)、局部配置模式(local configuration pattern，LCP)、局部相位向量化(local phase quantization，LPQ)和高斯图像金字塔(GIP)，从而提高了分类精度。Barmpoutis等[5]把每张图片看作一组多维信号，按照垂直方向和平行方向将每张图片按照图片大小、通道数、尺寸分割成小块，然后对每个小块创建木材图像的直方图表示，创建出一个新的描述符即V-H描述符，并用SVM分类器进行分类。Hu等[6]研究了基于ResNet18的深度学习策略将木材图像调整为256×256像素，研究局部分类。通过四个数据集进行了独立测试，其中80%的数据用于训练，20%的数据用于测试，该方法对每个数据集的分类准确度分别为98.16%、93.32%、96.64%和99.50%。当系统在Nvidia GTX860 GPU上运行时，对木材图像进行分类的平均时间为0.003 s。刁智多[7]选取颜色特征和缺陷特征进行融合得到最终的分选特征，然后采用人工鱼群神经网络、FNN神经网络作为木材分选分类器，人工鱼群神经网络分类器效果更好，准确率达到95%，分类时间0.073 8 s，利用动态阈值分割，特征筛选和形态学处理识别图片中的木板区域。李晖[8]构建多层神经网络分类器完成分类任务，采用30×10的小尺寸模板和170×30的大尺寸模板进行纹理提取，实测准确率为 94.17%。李超等[9]在Lab颜色空间内提取木材颜色低阶矩特征，应用纹理填充方法完成缺陷图像的分割，应用Contourlet 变换提取纹理特征，通过设计SVM 分类器完成颜色、缺陷和纹理分类。

目前，国内外使用机器视觉对木材表面进行无损检测的研究很多，对于木材表面颜色检测评估的方法也很多，但对木材的研究大多都是对不完整的木板图片进行分析。而对整块木板的评估应该立足于整体特征的评估，对木材片面的取样会导致对木材质量评估的不准确甚至错误。本文通过滚动引导滤波算法(rolling guidance filter，RGF)对木材表面图像进行滤波，然后提取木材的低阶矩作为特征向量，使用多层分类感知机(Multilayer Perceptr，MLP)对木材的颜色进行监督学习分类。

2 木材表面颜色算法

2.1 木材颜色分类的主要流程

目前对于木材表面的分类评估主要流程可以归纳为：①木材表面图像的预处理，包括对图片的增强、裁剪等；②预处理后木材表面图像对图片的色彩空间变换，然后提取颜色特征，如图片的一阶矩、二阶矩；③设计选择合适的分类器对木材进行分类，可以采用支持向量机(SVM)、多层感知机(MLP)、K邻近法(K-means)等。

2.2 木材图像的预处理

由于采集到的图像总会有噪声且由于木材表面本身存在气孔等产生微小的纹路，而这些微小的纹路对木材的评估是无效的，所以可以被视为噪点。对木材表面图像进行预处理需要对图像上因图像采集产生及本身微小纹路产生的噪点进行抑制。

联合双边滤波算法是一种综合考虑不同点间的空间距离和像素插值信息的非线性滤波技术，联合双边滤波算法将空间域的高斯滤波函数和颜色域的滤波函数结合，在平滑噪声的同时保持图像细小的颜色边界信息完整。双边滤波算法可表示为：

(1)

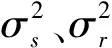
进一步可以写成：

(2)

其中：

(3)

滚动引导滤波器是一种基于滚动引导，通过迭代实现并且能够快速收敛的算法[10-11]。滚动引导滤波器首先通过高斯滤波对小结构细节进行过滤，将滤波后的图像作为引导图像，使用联合双边滤波器(joint bilateral filter)进行滤波，然后将滤波之后的图片作为新的引导图像，再使用联合双边滤波器进行滤波。

使用滚动引导滤波器迭代两次后对木材表面局部图像进行滤波的结果如图1所示，经过滚动引导滤波两次迭代后可以大大降低原图像上的噪点。

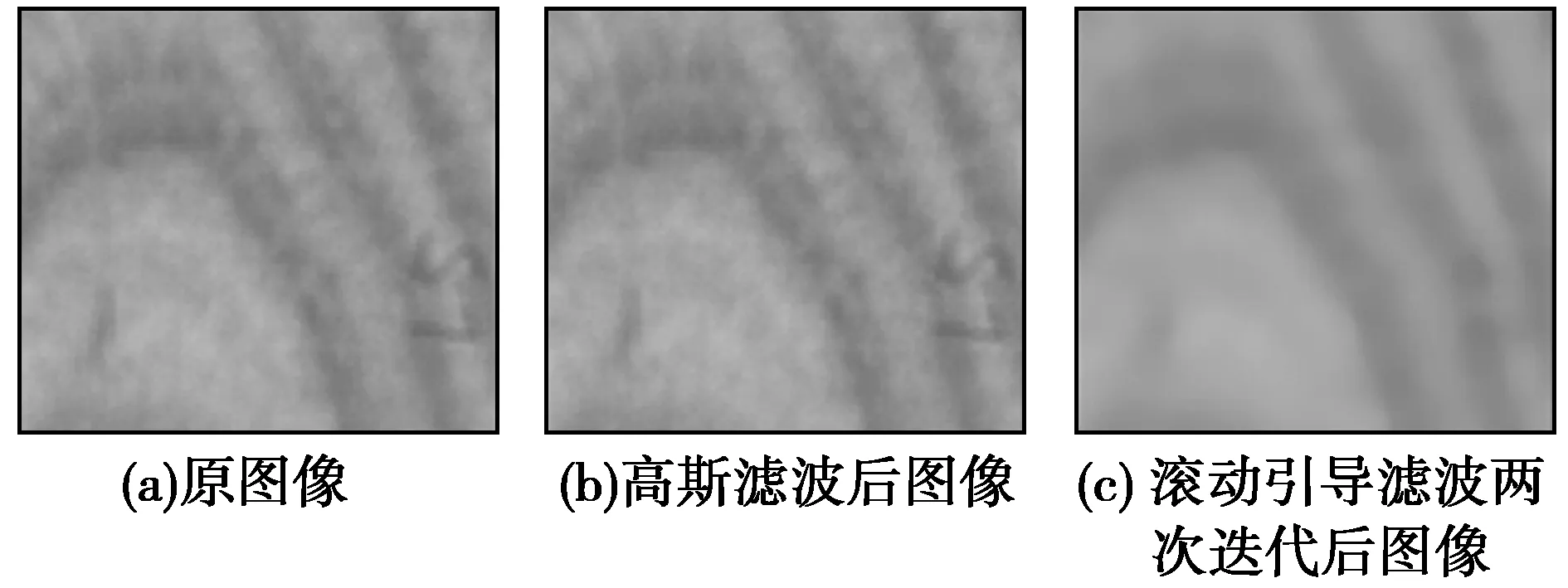
图1 滚动引导滤波器预处理木材局部图像

对木材图片进行形态学操作后进行边缘检测，裁剪木材图片，去除木材黑边，减少无关要素对图像的影响，之后对图片进行上述的高斯滤波与滚动引导滤波，通过滚动引导滤波得到预处理后的图像如图2所示。

2.3 木材图像颜色特征提取

木材表面的信息很多，对木材颜色特征的提取可以通过提取图像的低阶矩来实现，这一特征是基于图像整体的特征，可以较好地评价整块木材的整体水平。

由相机得到的图片一般是RGB空间的图像，RGB颜色空间直观易懂但是三个分量高度相关而且均匀性差。CIELab颜色模型是一种基于人眼生理特征的模型，L通道表示明度，a通道的颜色是从红色到深绿，b通道颜色是从蓝色到黄色[12]。

图2 经过预处理后的木材图像

由RGB颜色空间不能直接转化为CIELab，需要借助XYZ颜色空间，先把RGB颜色空间转化为XYZ空间后再转化为Lab颜色空间，RGB转化为XYZ空间方法如下：

(4)

之后再由XYZ颜色空间转化为Lab颜色空间：

(5)

(6)

(7)

其中：

(8)

颜色矩是一种简单有效的颜色特征表示方法，有一阶矩(均值，mean)、二阶矩(方差，variance)和三阶矩(斜度，skewness)等[13]，图片的颜色信息主要分布在低阶矩中，所以使用一阶矩、二阶矩、三阶矩就足以表达图像的颜色分布，提取的特征向量维数低。

三个颜色矩的数学定义如下：

(9)

(10)

(11)

其中：pi，j为图像在(i，j)处的像素值，μi为图像的一阶矩，σi为二阶矩，si为三阶矩。

为了更贴近人类的视觉感官，提高木材检测的速度，通过对图片提取R、G、B、L、a、b六个通道的颜色一阶矩和二阶矩，组成一个12维的特征向量来描述一张木材图片的颜色特征。

2.4 木材表面颜色分类原理

多层感知机MLP也叫人工神经网络(Artificial Neural Network，ANN)，包含一个输入层一个输出层以及若干隐藏层，多层感知机中隐藏层与输入层是全连接的，含有单层隐藏层的简单人工神经网络结构如图3所示。

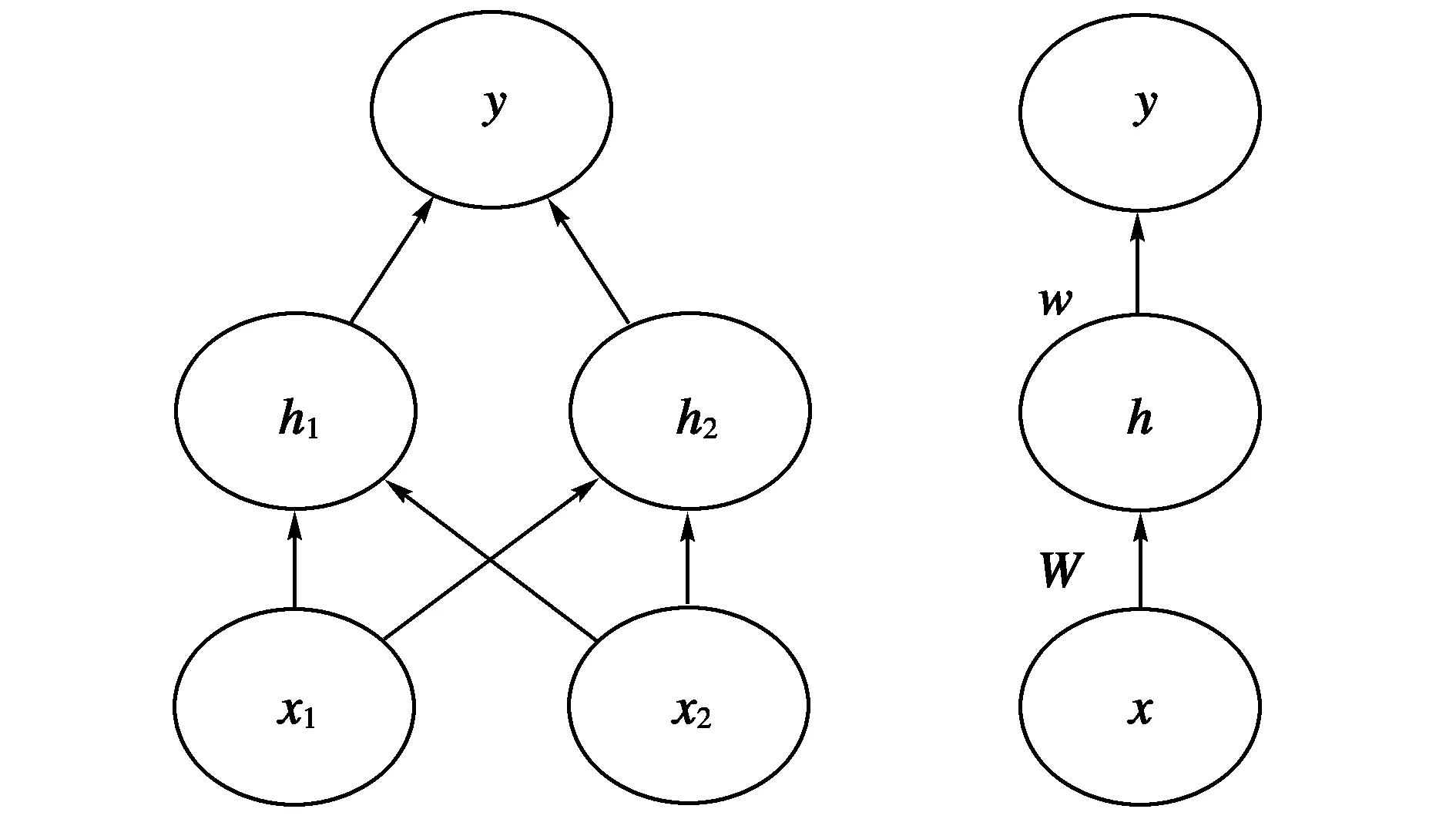
图3 简单人工神经网络结构

假设输入层的向量为x，选取h(x)为线性函数，则隐藏层为：

h=Wx+b

(12)

输出层的向量y为：

y=f(h(x))=f(Wx+b)

(13)

其中：W是权重，也称为连接系数；b是偏置，函数f多采用sigmoid函数或者tanh函数还有ReLU函数。如果隐藏层内不止一层，则隐藏层的输入为上一隐藏层的输出。

3 基于人工神经网络的木材颜色分类

3.1 木材颜色分类

对木材颜色进行分类需要综合考虑木材的色彩和纹理的分布，需要提取图像中表现颜色的特征值。本文采用的木材图像源自加拿大DALSA线扫描相机扫描得到的图像，该线状相机分辨率为2 048×2，最高行频为26 kHz，像素大小为7.04 μm×7.04 μm，像素位深为8 bits/12 bits。扫描得到的图片尺寸为2 048×18 000，将收集到的杉木、松木木材样本图像按照颜色分为A、B、C三类。木材的色彩多由其木种决定：杉木为浅红褐色，红杉、红松、核桃木为红褐色，在RGB空间中红褐色在(178，34，34)附近，黄褐色在(240，230，140)附近，在Lab空间中红木木材颜色明度L*分布在27.52～48.22范围内，a*分布在2.35～16.42范围内，b*分布在1.62～24.19范围内[14]。

对木材图像进行通道分解后绘制出A、B两类表面的RGB直方图进行对比，发现其在RGB三个通道上的像素分布差异很大，如图4所示，所以使用RGB三通道的颜色对木材的分类有较好的效果。而所有木材RGB三通道的像素均值在归一化后的RGB颜色空间内近似在一条直线上，如图5所示，样本中木材的颜色分布近似满足下式：

R+0.079G-0.735B-0.155=0

(14)

由此可见特定木材的颜色分布在一定范围内是稳定的，因此对于木材颜色在RGB空间内的研究是有意义的。在木材图像颜色变化不是很大的样本上，木材图像像素的均值可以作为一个比较好的描述木材图像整体颜色分布的特征。方差描述了图像在颜色域上分布的均匀性，正常木材的颜色不会出现较大的变化，纹理是局部颜色值与整体颜色不同的区域，所以可在一定程度上表现纹理区域的大小以及纹理的深度，三阶矩反映了图像颜色分布的对称性对于木材的颜色分类影响不大，而且计算三阶矩会大大增加计算时间，所以只采用一阶矩、二阶矩来描述木材图像的颜色特征。

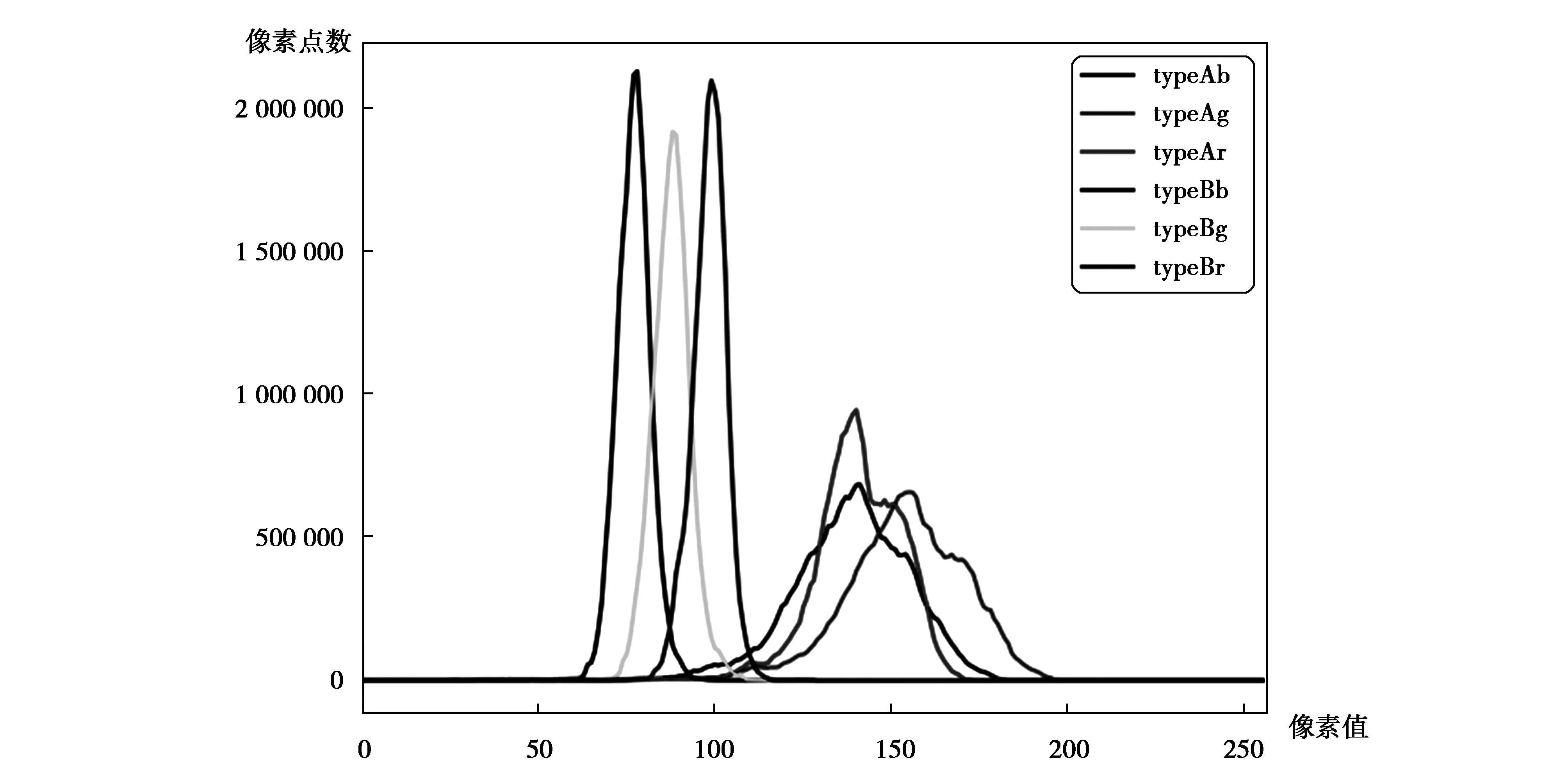
图4 A、B两类木材RGB三通道颜色直方图

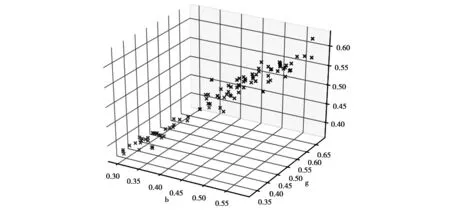
图5 木材图像均值在RGB空间上的分布

3.2 随机梯度下降

梯度下降算法是机器学习算法中求解最小值的一种重要算法，随机梯度下降(stochastic gradient descent，SGD)是梯度下降算法的一个扩展，其核心是梯度期望，从训练集中均匀抽取出一小批量样本，当训练集大小m增大时，小批量数目m′通常是固定的，损失函数L梯度的估计可以表示为：

金融产品在创新后，需要进行推广。首先，应该由专业的推广团队集中精力进行推广，促进市场占有率。若没有专业的推广团队，可以与其他公司合作，让更加专业的推广人员进行推广[6]。

(15)

使用来自小批量的样本，然后随机梯度下降算法使用如下的梯度下降估计：

θ←θ-∈g

(16)

其中：∈是学习率。

在实践中当训练集大小增大时不会延长模型达到可能的最优测试误差时间，因此可以认为使用随机梯度下降算法训练模型的渐进代价是关于数据集大小m函数的O(1)级别，所以在大的训练集中随机梯度下降法比梯度下降法可以使损失函数更快达到最优解。

3.3 交叉熵

机器学习算法中优化的过程就是减小损失的过程，其中分类问题的损失可以使用交叉熵(Cross Entropy Loss)作为损失函数。相对熵(relative entropy)又称为KL散度(Kullback-Leibler divergence)，其是两个随机分布之间距离的度量，记为DKL(p‖q)，定义为：

DKL(p‖q)=Ep[logp(x)-logq(x)]

=Hp(q)-H(p)

(17)

交叉熵也描述了两个概率分布p(x)、q(x)之间的距离，交叉熵越小说明二者越相似，其定义为：

CEH(p，q)=Ep[-logq]

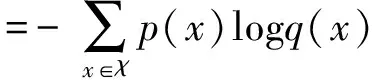
=H(p)+DKL(p‖q)

(18)

如果使用交叉熵作为模型的损失函数，则交叉熵越小，模型与实际数据的分布越接近。其中H(p)在p分布已知时为常量，所以最小化交叉熵就是最小化KL散度。

3.4 多层感知机(MLP)分类

较为复杂的多层感知机可以有若干层隐藏层，经过实验选定了如下结构的MLP模型，其中每层隐藏层采用线性函数，输入为对图片提取的12维颜色矩特征向量，输出木材分类为A、B、C三类的概率向量。其中激活函数使用ReLU函数激活，损失函数使用交叉熵，以0.000 5为SGD算法迭代过程中的学习步长，对损失函数求解最小值。多层感知机模型如图6所示。

将采集得到的320张木材图片经过人工按色彩深浅分类后分别设置标签为A、B、C，选取A类23张、B类22张、C类35张共80张作为测试集，剩余A类60张、B类84张、C类96张共240张作为训练集进行训练，训练集迭代200次后测试集的准确率最终可以达到96.25%。训练集的损失函数图像如图7所示，训练集的损失函数在迭代25次左右可以达到最小值。

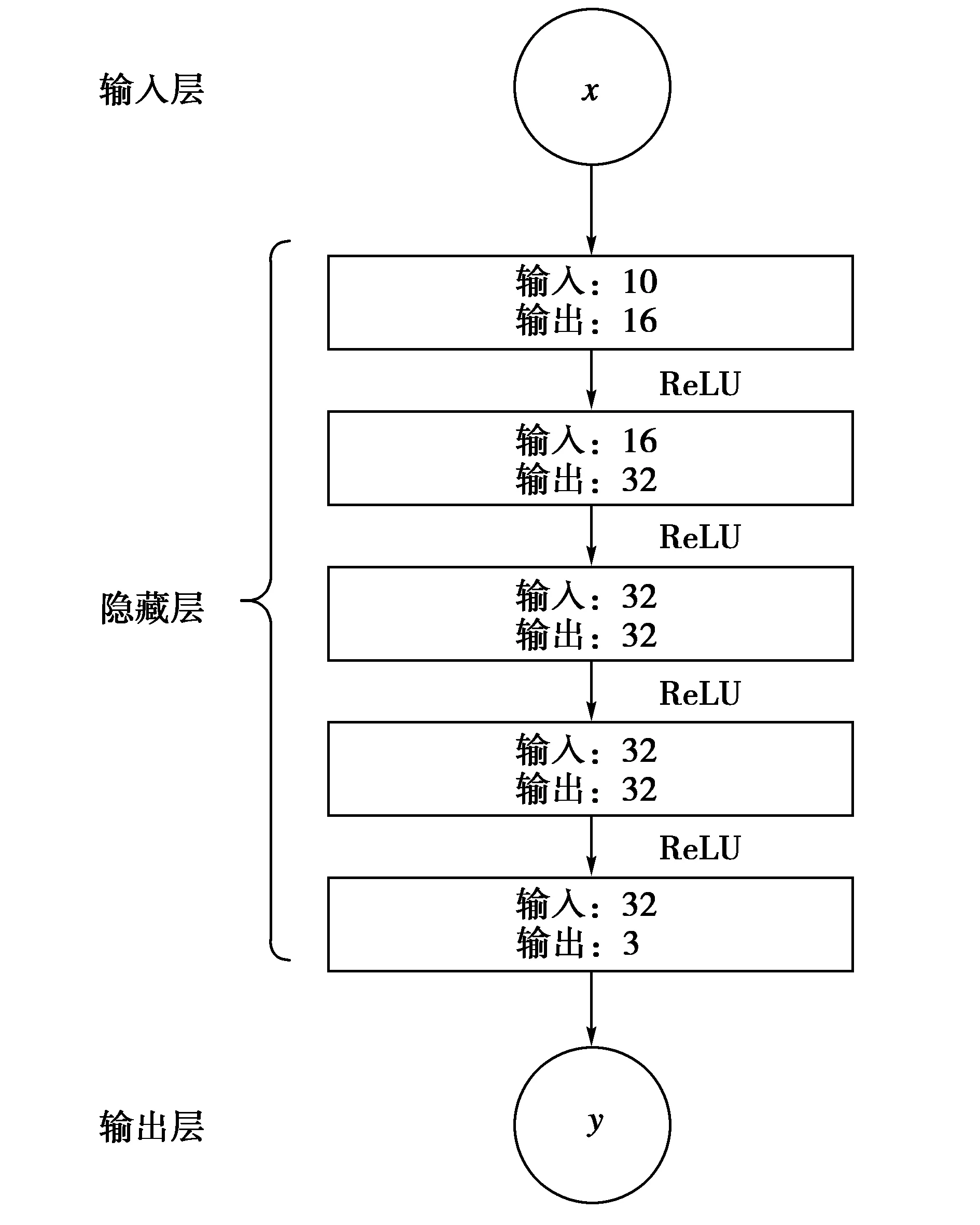
图6 多层感知机模型

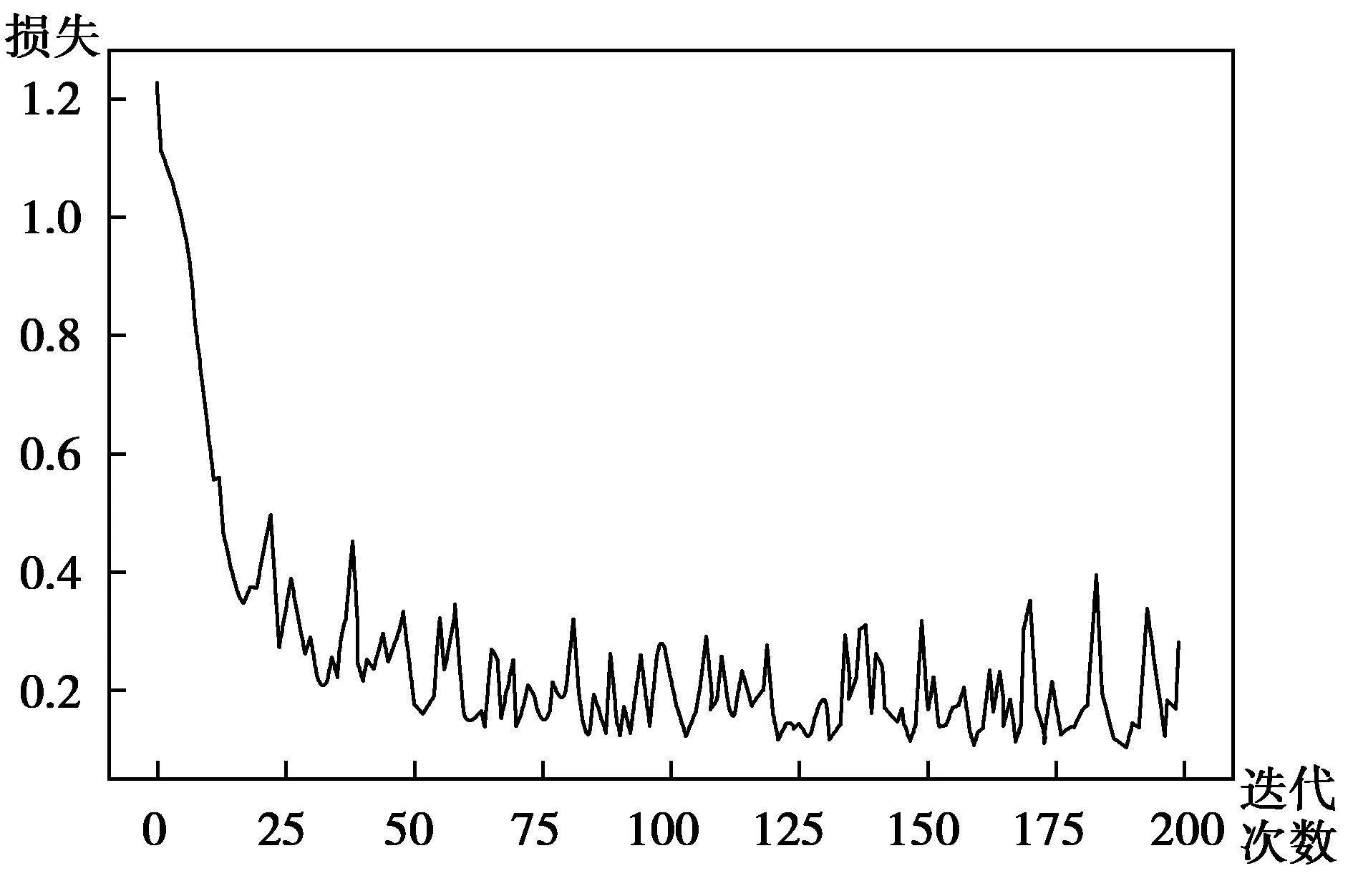
图7 训练集损失函数

4 结论

随着我国木材市场需求的不断扩大，受人们主观因素以及劳动强度等因素的制约，人工对木材分类，准确度和效率无法保证，难以满足国内的市场需求。针对该问题，本文采用python opencv软件对木材表面进行边缘检测、高斯滤波、滚动引导滤波等操作，通过图像增强实现了木材表面图像的去背景化，通过提取木材图像RGB、Lab空间的低阶颜色矩作为颜色特征，采用MLP多层分类感知机对图像进行分类。本算法采用320张无缺陷的木材图像作为训练测试样本，其中240张为训练集，80张为测试集，最高可以达到96.25%的准确率，效果较好。在实际运用中对于较大图片采取滚动引导滤波会大大增加处理时间，对于有缺陷木材的分类也会产生问题，还需后续深入研究。