阀控液压马达角位移随动系统动态特性研究

闫 政

(晋中学院机械学院， 山西晋中 030600)

引言

阀控液压马达作为一种典型的液压控制系统，广泛被应用于矿山、建筑及工程机械等领域[1]。根据被控物理量的不同，阀控液压马达可以分为阀控马达角位移控制系统和角速度控制系统。然而， 现有针对阀控液压马达系统的控制方法多是基于PID控制器实现对马达输出轴转角和转速的控制，虽然这种方法具有简单易实现的优点，但就设计而言，不具有任意性，且PID参数整定过程需要很强的经验性[2]。为此，对阀控液压马达控制器设计方法进行改进，对改善系统控制特性具有重要意义。

针对阀控液压马达系统的控制特性，李军等[3]建立了阀控液压马达角位移控制系统的数学模型，并通过仿真验证了所建立模型的正确性；DASGUPTA K等[4]基于键合图仿真技术构建了伺服阀控液压马达系统的仿真模型，并对伺服阀PI控制器参数对系统动态特性的影响进行仿真分析；JIANG等[5]提出一种基于模糊神经网络控制的阀控马达角速度智能控制方法，并利用MATLAB软件进行仿真分析，研究结果表明，所提出的智能控制方法能够提高阀控马达系统的自适应能力与鲁棒性；王存堂等[6]以提高叶片马达速度控制精度为目的，结合理论模型建立了高速开关阀控叶片马达的数学模型，并基于 PID 控制算法对该系统进行仿真分析，证明了PID控制器对该系统具有良好的转速控制效果；杨前明等[7]以某阀控双马达角速度控制系统为对象，将PID控制器应用到基于PLC的速度同步控制方案中，通过仿真研究证明了PID控制器能够提高系统的同步控制性能；杨国来等[8]建立了阀控液压马达速度控制系统的数学模型，并基于MATLAB/Simulink软件对系统进行仿真分析，研究结果表明：PID控制器能够改善系统的抗负载性；雷晓顺等[9]针对阀控马达速度系统采用PID控制器时易受负载干扰的缺陷，提出采用模糊PID控制算法，通过计算机仿真和试验研究表明，采用模糊PID控制器，可以改善阀控液压马达恒转速控制系统的抗负载性能。毕世书等[10]针对阀控液压马达速度控制系统中采用PID控制器存在的参数整定复杂且鲁棒性较低的问题，提出采用遗传算法对系统PID控制参数进行优化，通过仿真实验证明了该方法能够提高系统的鲁棒性及动态特性。晋民杰等[11]以某型液压起重机为研究对象，建立了基于PID控制器的阀控液压马达系统的闭环控制系统， 并对PID参数进行非线性优化，改善了系统的控制特性；KUMAR S等[12]针对比例阀控液压马达特性进行了仿真与试验研究，结果表明：采用闭环控制可以降低系统对负载变化的敏感度，且闭环反馈增益系数会对系统稳定性与能效产生影响。

综合分析上述研究可知，现有针对阀控液压马达控制特性的研究多是基于PID控制算法，其在控制器设计时需要在参数整定方面具有很强的经验性。另一方面，PID控制方法属于经典控制范畴，其设计过程不具有任意性。此外，现有研究多是针对阀控液压马达速度控制系统的控制特性进行研究，而对阀控液压马达位置控制系统的研究较少。

针对上述问题，本研究采用极点配置法对阀控液压马达角位移控制系统进行设计，并对基于PID闭环控制、极点配置法及含有状态观测器的极点配置法的阀控液压马达角位移控制系统特性进行对比研究。简要介绍阀控液压马达系统工作原理；分别建立阀控液压马达角位移控制系统的传递函数、方框图以及状态空间表达式，并对该系统的时-频域特性与能控-能观测性进行分析；在此基础上，分别基于3种控制方法对阀控液压马达角位移控制系统进行设计，并利用MATLAB/Simulink软件对系统阶跃响应进行了仿真分析，以对比各控制方法在阀控液压马达系统中的应用效果以及状态观测器极点位置对系统动态特性的影响，为改善阀控液压马达系统的动态特性提供理论依据。

1 阀控液压马达工作原理

阀控液压马达是一种典型的开式液压系统，主要包括动力元件(液压泵)、控制元件(三位四通阀)、执行元件(液压马达)以及外部负载，其原理图如图1所示。通过控制三位四通阀的位置以及开度实现对液压马达输出轴角速度和角位移的控制。

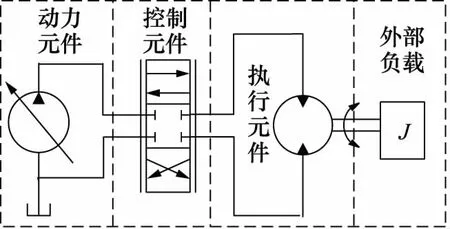
图1 阀控液压马达系统原理图

2 阀控液压马达数学模型

2.1 传递函数及方框图

为了建立阀控马达角位移控制系统的传递函数和方框图。首先，在假定三位四通阀为零开口四边滑阀，液压泵出口压力恒定不变，油箱压力为0的基础上，设系统的负载流量为QL，流量增益系数为Kq，滑阀阀芯位移为Xv，流量-压力增益系数为Kc，负载压力pL，则滑阀的线性化流量基本方程为：

QL=KqXv-KcpL

(1)

其次，在忽略三位四通阀与马达之间管路的压力损失及动态特性的前提下，设马达排量和输出轴旋转角度分别为Dm和θm,马达两边腔室及管路的等效总体积和泄漏系数分别为Vt和Ctm，马达的输出轴及外部负载的等效转动惯量为Jt, 黏性阻尼系数为Bm，外部负载扭矩及弹簧刚度分别为TL和G，建立液压马达的流量连续性方程与外负载平衡方程如式(2)和式(3)所示：

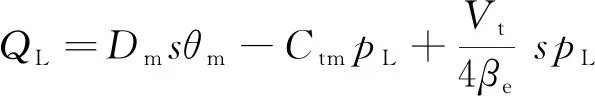
(2)

pLDm=Jts2θm-Bmsθm+Gθm+TL

(3)

根据上述式(1)～式(3)所示的阀控马达基本方程，绘制阀控马达角位移控制系统方框图如图2所示，图中，输入信号为液压阀芯位移，输出量为液压马达输出轴的旋转角度。同时，联立上述基本方程，消去相应的中间变量，便可以得到马达输出轴转角公式如式(4)所示：

(4)

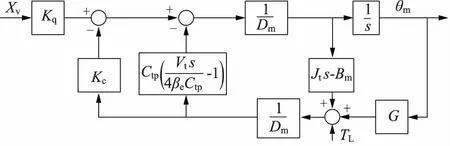
图2 液压阀控马达系统方框图

阀控液压马达系统的外部负载多为惯性负载[13]，即外负载扭转弹簧刚度G一般为0，且马达与负载之间的黏性阻尼系统极小(忽略不计)。 因此，将式(4)进行化简，可以得到阀控液压马达角位移控制系统的传递函数为：

(5)

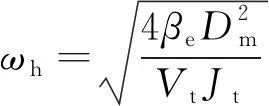
2.2 系统状态空间表达式

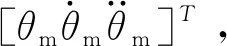
(6)

3 阀控液压马达系统特性分析

以某阀控液压马达系统为研究对象，对系统时域、频域特性、能控及能观性进行分析，为后文闭环控制系统设计奠定基础。所述阀控马达系统中的滑阀流量增益和流量-压力系数分别为1.5×10-16m3·s-1·Pa-1和4 m2·s-1，马达输出轴所连接外部惯性负载及其输出轴的等效转动惯量为0.2 kg·m2，马达主要参数如表1所示。

根据推导过程，代入具体参数，得到该阀控马达角位移控制系统的传递函数如式(7)所示：

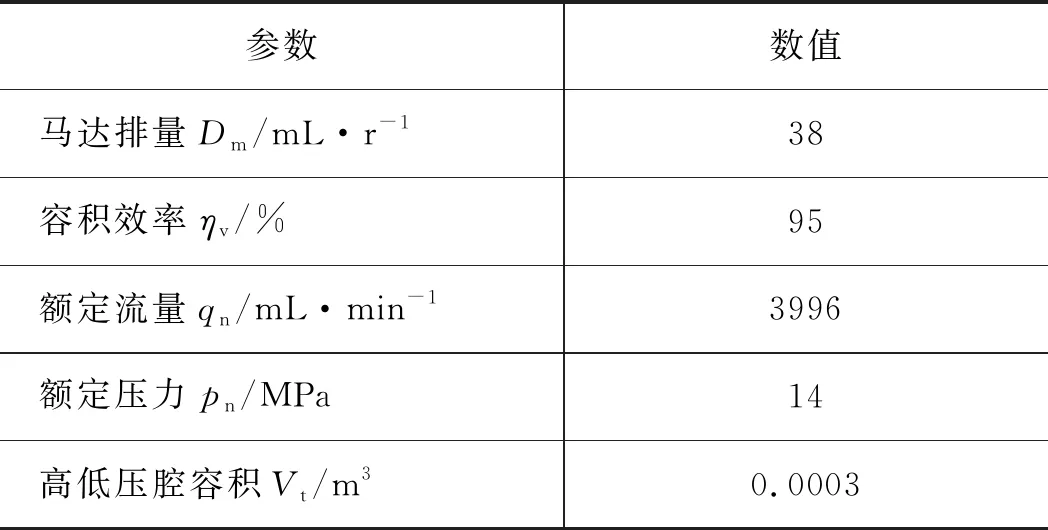
(7)

需要注意的是，这里得出的传递函数是指系统开环传递函数。图3为利用MATLAB软件绘制的系统极点分布位置示意图，由图可知，该系统开环传递函数的3个极点分别为0和-11±39.5i，存在零极点，故该系统为非最小相位系统。

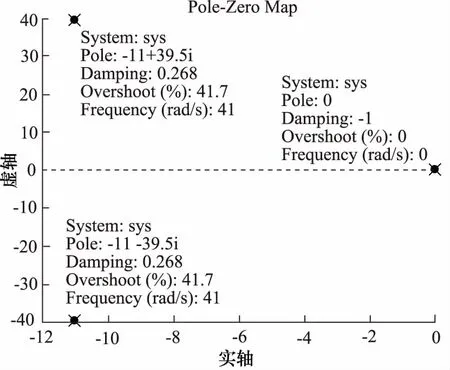
图3 极点分布位置示意图

3.1 时域分析

图4和图5为阀控液压马达角位移控制系统的开环单位阶跃响应曲线和单位脉冲响应曲线，由图4可知，该系统的单位阶跃响应曲线随时间的推移呈现出无限上升的趋势，这是因为当系统输入信号为单位阶跃信号时，根据Laplase变换的终值定理，可得其稳态输出值为：

(8)

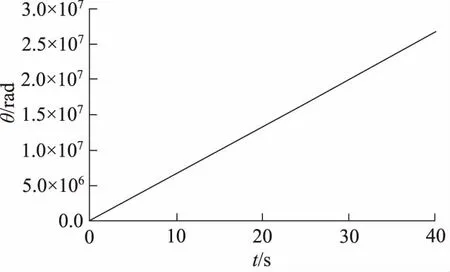
图4 单位阶跃响应曲线

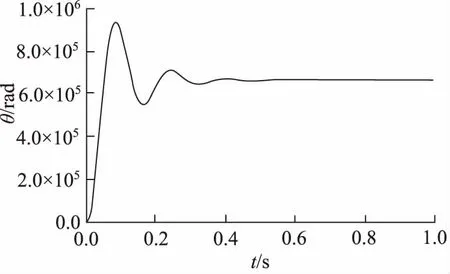
图5 单位脉冲响应曲线

由图5可知，该系统的单位脉冲响应曲线随时间的推移呈欠阻尼震荡并最终到达恒定值，究其原因，是因为当输入信号为单位脉冲信号时，根据Laplase变换的终值定理，其稳态输出值为：

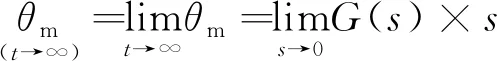
=6.67×105

(9)

3.2 频域分析

图6和图7为该系统开环传递函数的奈奎斯特图和伯德图，由图6可知，系统开环奈奎斯特图曲线按照逆时针方向包围(-1，j0)点2圈，而系统开环传递函数在[s]右半平面没有极点，根据奈奎斯特稳定性判据，可以判定该阀控液压马达角位移控制系统是闭环不稳定，开环稳定的。另外，由图7可知，系统的幅值裕度Kg和相位裕度γ均为负值，同样印证了系统闭环不稳定的结论。

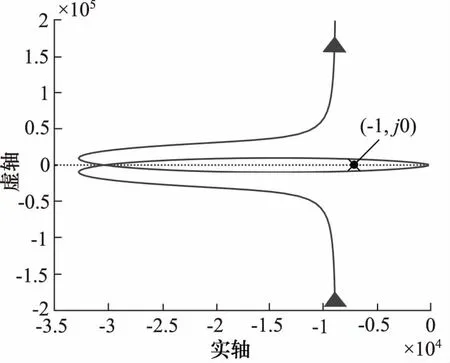
图6 奈奎斯特图

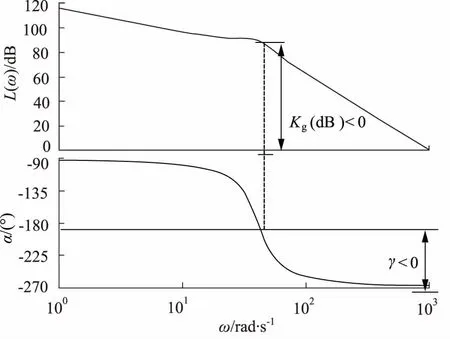
图7 伯德图

3.3 能控能观性分析

系统的能控性与能观性是实现状态反馈控制的基础，因此，需要结合阀控马达系统的具体参数，对该系统的能控性与能观性进行分析，该系统的状态方程与输出方程为：

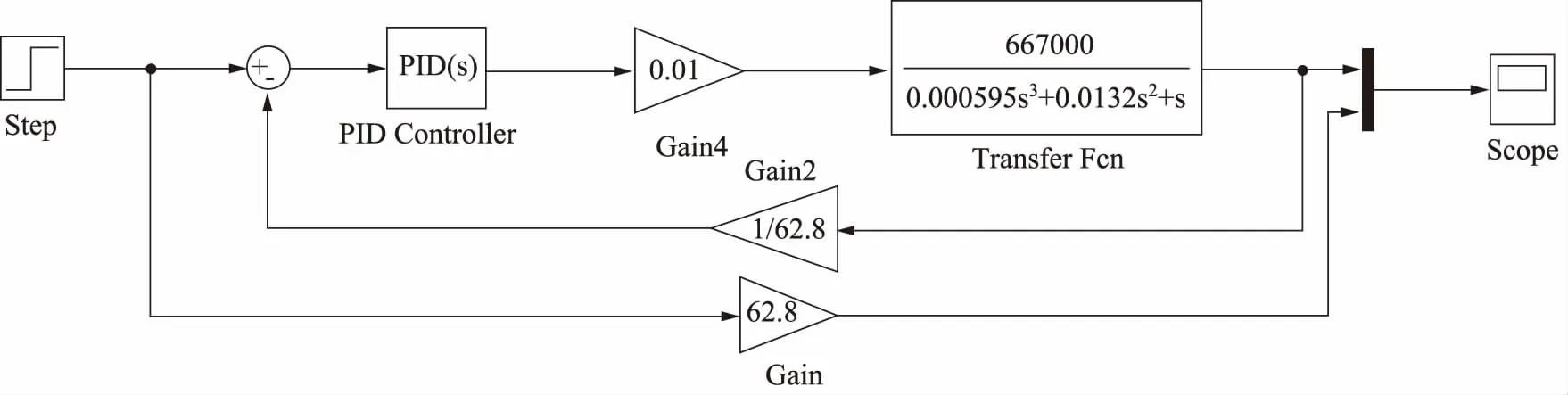
图8 PID控制闭环仿真模型图

(10)

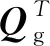
(11)

(12)

由上述公式可知，该系统的能控性矩阵与能观测性矩阵均满秩，故该系统完全能控且能观测，这为进行状态反馈控制系统设计奠定了基础。

4 闭环控制系统设计及对比分析

假设该阀控液压马达角位移控制系统的控制要求为：阀芯移动0.01 m，液压马达的输出轴角位移在0.5 s内达到62.8 rad(20圈)，超调量Mp小于5%，超调时间tp小于0.3 s，系统频宽ωb小于50 rad/s，稳态误差ep为0，分别采用PID、极点配置法和含有状态观测器的极点配置法设计闭环控制系统，并利用MATLAB/Simulink对3种方法的控制特性进行仿真分析与对比。

4.1 基于PID控制器的闭环控制系统设计

基于PID控制器的阀控液压马达角位移控制系统的基本原理为：输入量与反馈量(输出值)进行比较构成系统偏差，并通过PID控制器对系统的偏差进行调节，以使系统的输出尽量接近期望值，在系统设计过程中，如何设置合理的PID调节参数(即比例、积分、微分系数)是影响系统控制性能的关键[14]。图 8为基于PID控制器的阀控液压马达角位移闭环控制系统Simulink仿真模型。

4.2 基于极点配置法的状态反馈控制系统设计

基于PID控制器的闭环系统设计属于经典控制理论范畴，无法实现对闭环系统极点的任意配置，只有采取引入附加校正网络，通过增加开环零极点的方法以变更轨迹走向，从而使系统极点落在指定的期望位置上，这样增加了控制系统的难度。为克服这一缺点，基于现代控制理论的分析方法，在实现状态反馈控制系统的基础上，采用极点配置法，根据所期望的控制性能指标，直接对该系统极点位置进行配置。

该阀控液压马达角位移控制系统完全能控且能观测的，其能控规范型为：

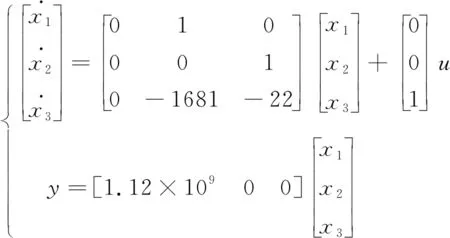
(13)

在确定了系统能控规范型的基础上，需要根据所期望的控制性能指标以确定所希望的3个极点位置。选定s1和s2为1对主导极点，另外1个极点为远极点。该系统的性能主要由主导极点s1，s2决定，远极点的影响甚微。

首先需要确定主导极点位置，根据二阶系统的性能指标关系式，系统超调量一般小于5%，可得：

(14)

式中，ξ为系统的阻尼比。

由式(14)可知，系统阻尼比ξ≥0.707。在工程中，二阶系统阻尼比一般在0.4～0.8之间[15]，故选取ξ为0.707。

由系统超调时间小于0.3 s，可得：

(15)

(16)

式中，ωn为系统的自振频率。

此外，二阶系统的频宽ωb与自振频率ωn有如下关系：

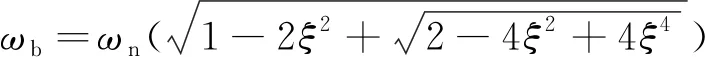
(17)

根据控制性能指标，系统频宽ωb小于50，且系统阻尼比ξ选定为0.707，代入式(17)可得：系统自振频率ωn≤50，这里取自振频率ωn为50。至此，根据式(17)便可以得到该系统的主导极点为：

(18)

在此基础上，选取远极点为与原点距离远大于5倍主导极点与原点距离的点，因此，选择远极点s3为-500。

由期望极点所构成的特征多项式为：

f*(s)=(s+500)(s2+70.72+2500)

=s3+570.72s2+37850s+1250000

(19)

结合原系统特征多项式，可得状态反馈矩阵为：

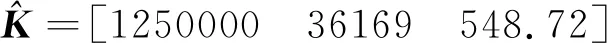
(20)

至此，可以得到进行极点配置后的状态反馈闭环系统的传递函数为：

式中，L为输入放大系数。

由系统控制要求可知，系统稳态误差为0，即：

(22)

将式(21)代入式(22)中，可得系统输入放大系数L为0.07。在MATLAB/Simulink中建立基于极点配置法的状态反馈闭环控制系统模型如图9所示。

4.3 含有状态观测器的状态反馈系统设计

采用极点配置法的阀控液压马达角位移控制系统是以状态反馈为基础的，然而，当系统所需反馈的状态变量无法通过直接测量得到时，就需要构造状态观测器，以观测器输出的状态来代替系统实际状态，进行状态反馈。为分析加入观测器后对系统的影响，以阀控马达角位移控制系统为例，建立含有状态观测器的状态反馈闭环控制系统。

该系统完全能控且能观测，故该系统及状态观测器的极点可以任意配置。含有状态观测器的极点配置法状态反馈系统的控制性能与前文未加入时相同，故此时闭环系统的期望极点和状态反馈矩阵不变，只需要对相应的状态观测器进行设计，设状态观测器的极点位置为s1,2,3=-500。

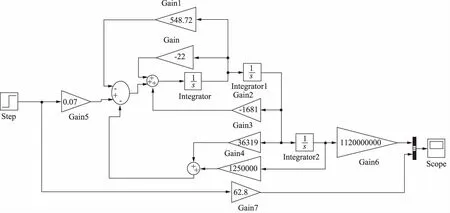
图9 极点配置法状态反馈闭环控制系统仿真模型

在设计状态观测器时，需要将系统转化为能观测规范型，所需变换矩阵T的计算方法为：

T=[T1,AT1,A2T1]

(23)

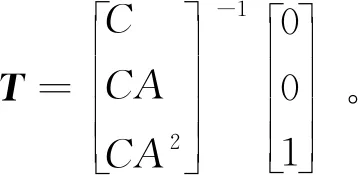
得到变换矩阵后，可得到系统能观测规范型为：

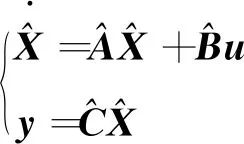
(24)

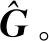
(25)

状态观测器的特征多项式为：

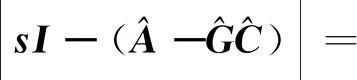
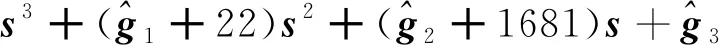
(26)

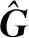
(27)

给定系统的反馈矩阵G为：

(28)

状态观测器的状态方程为：

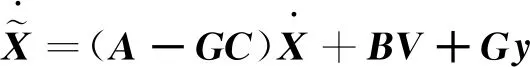
(29)

基于上述过程，在MATLAB/Simulink中搭建含有状态观测器的极点配置状态反馈模型如图10所示。

4.4 仿真对比

利用MATLAB/Simulink软件对采用上述3种控制方法的阀控液压马达角位移控制系统特性进行仿真分析。其中，当采用PID闭环控制系统时，通过设置不同PID控制参数进行仿真对比，选择较为合适的PID参数(Kp=0.4,Ki=0.001,Kd=0.0001)；当采用基于极点配置法的状态反馈控制系统时，各项参数均按照前文所得的计算结果进行设置，最终得到如图11所示的阶跃响应曲线。由图可知，采用3种控制方法均能达到系统的控制要求，然而，当采用PID闭环控制系统时，系统响应较慢，约0.4 s左右才能达到期望输出角位移，且存在明显的震荡；而采用极点配置法和含有状态观测器的极点配置状态反馈控制系统响应速度较快，在0.2 s左右即可达到稳定的期望输出角位移，且阶跃响应曲线几乎不存在震荡。

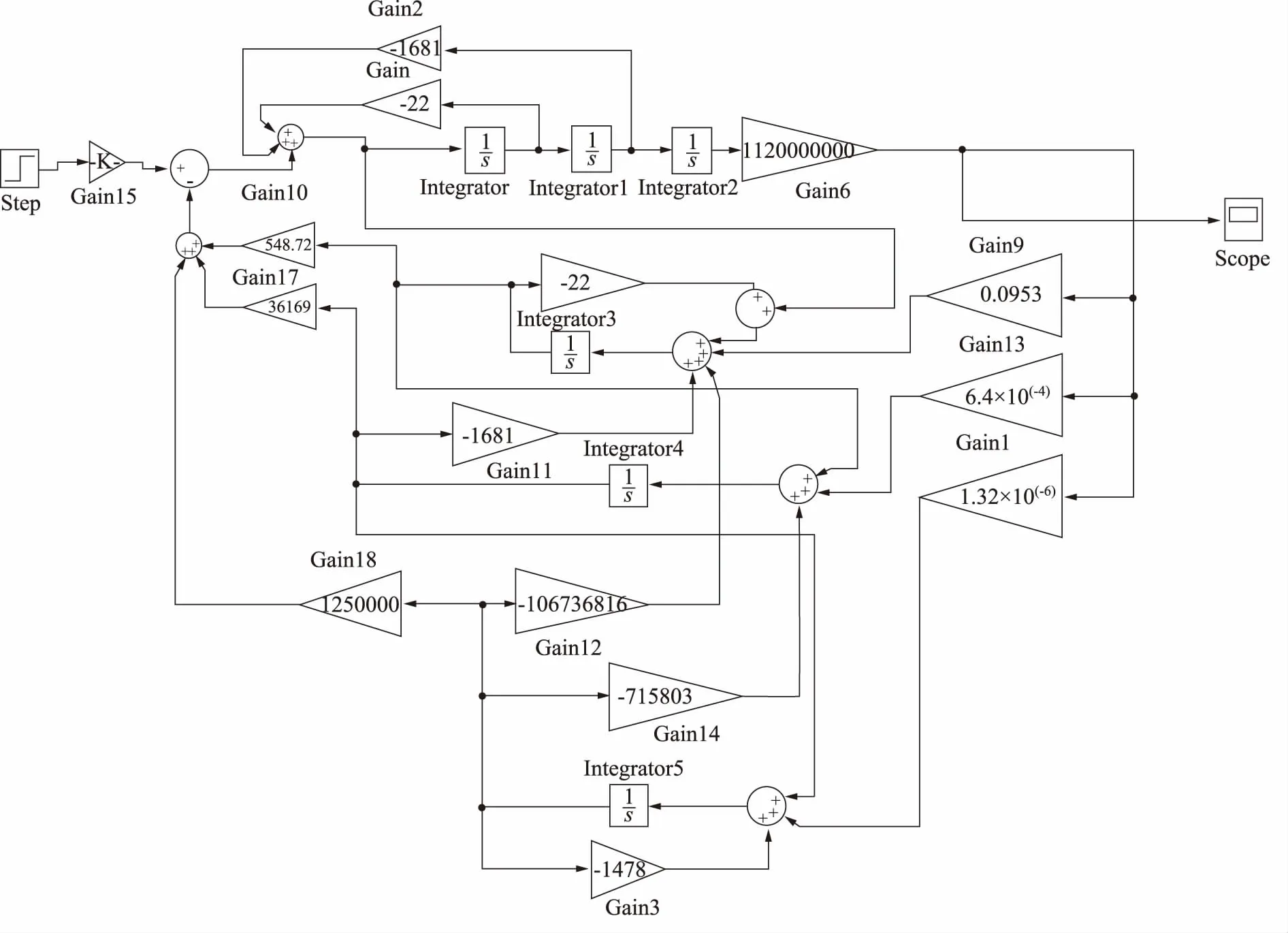
图10 含有状态观测器的极点配置状态反馈系统仿真模型

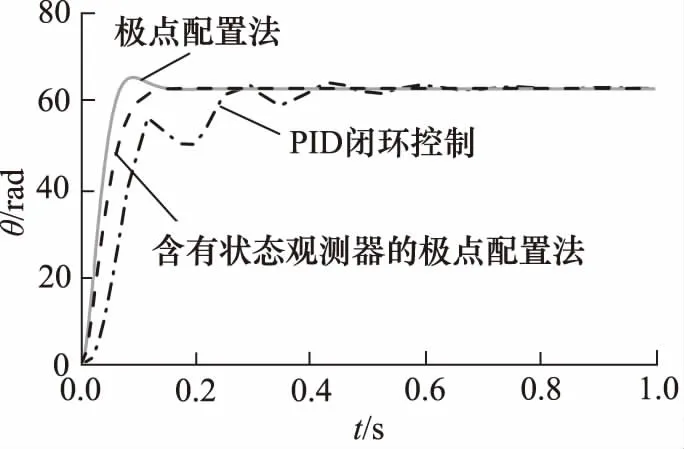
图11 阀控马达角位移控制系统阶跃响应曲线

为探究状态观测器的极点位置对阀控液压马达角位移控制系统性能的影响，分别将状态观测器的极点s1,2,3配置到不同位置，建立相应的状态反馈闭环控制系统模型，通过仿真进行对比分析。

图12为将状态观测器极点分别配置到不同位置时，阀控液压马达角位移控制系统的阶跃响应曲线，由图可知，状态观测器极点位置会对系统输出角位移控制特性产生影响，在一定范围内，极点位置距离原点位置越远，阶跃响应曲线超调量越小(甚至无超调)，但极点位置对阶跃响应曲线的调整时间影响不大，输出角位移均可在0.2 s左右达到稳定的期望输出值。

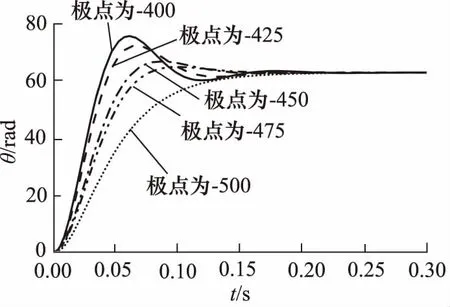
图12 状态观测器不同极点对应的阶跃响应曲线

5 结论

本研究以某型阀控液压马达角位移控制系统为研究对象，分别基于PID闭环控制、极点配置法以及含有状态观测器的极点配置法对系统动态特性进行了对比研究，得出如下结论：

(1) 相对于PID闭环控制法，极点配置法在阀控液压马达角位移控制系统设计过程中更加灵活，可以根据期望的控制性能指标，实现系统极点的任意配置；

(2) 当采用含有状态观测器的极点配置法对状态反馈闭环进行设计时，虽然状态观测器的极点可以任意配置，但其位置会对系统控制特性产生影响，随着极点位置与原点之间距离的逐渐增大，系统超调量逐渐减小。