塔机起重臂根部铰点水平静位移试验方法探讨

米成宏，李玉杰

（徐工集团徐州建机工程机械有限公司，江苏 徐州 221000）

对于塔式起重机（以下简称“塔机”）塔身这种大长细比的结构，其稳定性校核是设计的关键，原则上只要塔机的强度、稳定性校核满足要求，则认为塔机是安全的。但考虑到我国塔机厂家众多，各厂家设计水平参差不齐，不能保证塔身的整体稳定性可以得到合理的校核，因此GB/T 13752-2017《塔式起重机设计规范》明确规定了水平静位移的计算方法及限值；GB/T 5031-2019《塔式起重机》也规定了水平静位移的限值；TSG Q7002-2019《起重机械型式试验规则》也要求塔机刚度应符合相应标准要求。但相关标准只给出了水平静位移的理论概念和计算方法，没有给出其具体检测方法，导致检测出的结果与计算结果有很大差异，给水平静位移的检测造成了一定的困扰。

1 相关标准对塔机水平静位移的定义

1）GB/T 13752-2017《塔式起重机设计规范》5.6.2 条规定了塔机起重臂根部连接处的水平静位移不大于1.34h/100，其中h为起重臂根部连接处至直接支撑整个塔身的平面的垂直距离，水平静位移可按式(1)计算

式中 Δx——起重臂根部连接处的水平静位移，mm；

N——塔身与臂架连接处以上塔身顶部所有垂直力的合力，N；

NE——欧拉临界载荷NEx和NEy中的较小者，N；

ΔM——塔身中心线处的弯矩M 引起的起重臂根部连接处的水平位移，mm。

从式(1)可以看出，塔机的水平静位移大小与塔机吊载时的弯矩成正相关（图1），水平静位移初始点为塔身没有任何弯曲变形时的A 点，水平静位移终止点为变形后的B点，距离Δx为水平静位移。

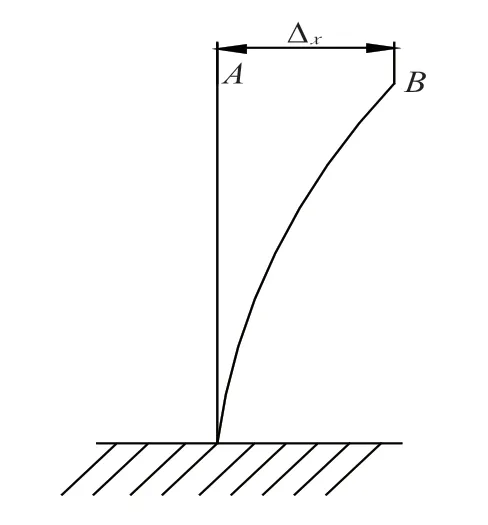
图1 水平静位移示意图

2）《起重机设计手册（上）》中明确规定塔机的水平静位移，其值ymax按图2 所示的非线性力学模型分析。

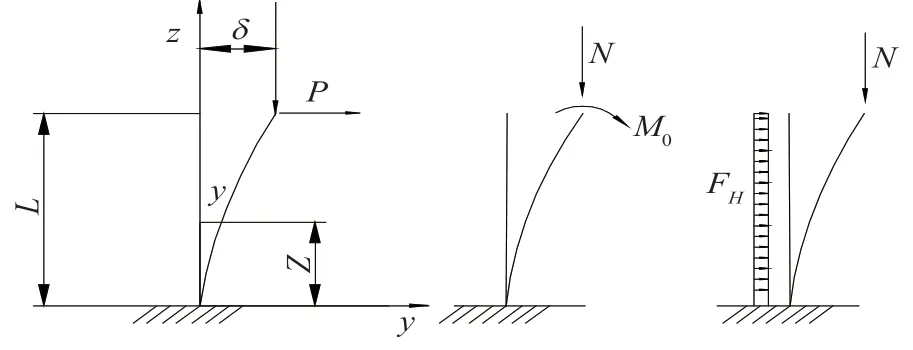
图2 水平静位移非线性力学模型

可近似用式(2)进行计算

式中P——塔顶上的横向力;

M0——塔顶上的端弯矩;

FH——作用于塔身的均布横向力;

N——塔顶上作用的轴向力，应计入塔身1/3 的自身重力；

NE——一端固定另一端自由轴心压杆的临界力，；

L——塔身高度；

EI——塔身的抗弯刚度。

可以看出，塔机水平静位移的概念是自图1塔身没有任何弯曲变形时的A点为初始点到变形后的B点为终止点的距离，大小为Δx,由于二阶效应放大系数，故式(2)计算的水平静位移值较式(1)计算出的水平静位移值更大。令

则

式中 ΔM0——端弯矩M0产生的分项水平位移；

Δf——风载荷P、FH产生的分项水平位移。

3）GB/T 3811-2008《起重机设计规范》规定塔机在额定起升载荷(有小车时还应包括在臂端的小车自重载荷)作用下，塔身在其臂架连接处(或臂架与转柱的连接处)产生的水平静位和ΔL与塔身自由高度H的关系，推荐为:ΔL≤1.34H/100，其计算宜采用非线性分析方法。可以推断，水平静位移初始点仍为图1 中塔身没有任何弯曲变形时的A点。

4）GB/T 5031-2019《塔式起重机》规定在额定载荷作用下，塔机起重臂根部连接处的水平静位移应不大于1.34H/100（H为最大独立状态下起重臂连接处至塔机基准面的垂直距离）。TSG Q7002-2019《起重机械型式试验规则》规定塔机刚性要求应符合GB/T 5031-2019《塔式起重机》和设计文件规定，但两者均未明确规定水平静位移的具体检测方法。

综上所述，水平静位移的标准概念应是图1中的Δx，其初始点为塔身没有任何弯曲变形时的A点，终止点为变形后的B点，概念一旦明确，使用这个概念的任何环节（设计、检测、使用等）均应严格遵守，不能存在一个概念多种理解、多种操作或者偷换概念使用的现象。

2 水平静位移按国家标准计算实例

以某款型号为QTZ125 的塔机为例，其塔身高度为46.7m，最大幅度60m，臂端最大额定起重量1.5t。

采用比较保守的式(2)进行计算，为方便计算，统一按标准节的抗弯刚度进行计算，工况为臂端60m 吊载臂端最大额定起重量1.5t 并考虑风压为250Pa 的尾吹风，载荷及参数如表1 所示。

表1 水平静位移计算参数及载荷

经计算其水平静位移为

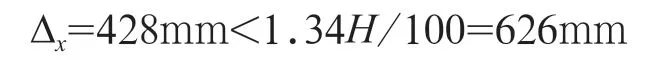
满足标准，且仅达到0.92H/100，与标准相比还有很大的富余度。

3 水平静位移型式试验检测实例

某型式试验检测机构按照TSG Q7002-2019《起重机械型式试验规则》的要求对上述型号为QTZ125 的塔机进行了水平静位移检测。测试方法如图3 所示：以小车处于最小幅度，吊钩处于最大高度，空载状态C点作为水平静位移初始点；以小车处于最大幅度60m，吊载臂端最大额定起重量1.5t 砝码，重物稍离地面时B点为水平静位移终止点。水平静位移测试值为820mm，达到了1.76H/100，检测值为计算值的1.92 倍。

图3 型式试验检测示意

4 理论计算与型式试验检测数据差异分析

从GB/T 13752-2017《塔式起重机设计规范》和《起重机设计手册》等可以看出，水平静位移初始点为图4 中A点，终止点为B点，大小为Δx=Δm0+Δf，实际检测的水平静位移初始点为不吊载后倾时的C点，终止点仍为B点，大小为Δm1=Δm0+Δx0（Δx0为无风时，不吊载后倾弯矩产生的位移）。此时

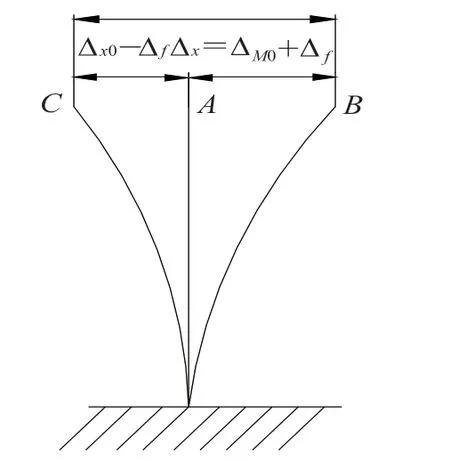
图4 水平静位移计算与检测对比图

即检测到的水平静位移比标准概念值多了Δx0，少了风载荷P、FH产生的位移Δf。导致理论计算与型式试验检测数据存在较大差异。

型式试验检测该水平静位移应为

导致型式试验检测数据错误的根源是水平静位移的概念使用错误，相关标准也未明确规定测量方法，导致理论计算与检测不统一。

5 型式试验检测方法探讨

从各标准及相关文献不难看出，应该将图4塔身没有任何弯曲变形时的A点作为水平静位移检测的位移初始点，水平静位移检测需要先找到位移初始点A，仍以测试塔机为例，推导出以下几种检测方法。

5.1 方法一

如图5 所示，风载荷沿x正向吹，当起重臂指向x负向时，小车移动到最小幅度，吊钩升至最大起升高度，不吊载，此时塔身产生Δx0+Δf位移，测量初始点C1 的位置，旋转180°，在反方向产生Δx0-Δf位移，测量终止点C位置，此时测得的位移为Δx2，则

图5 Δx0求解示意图

小车处于最小幅度，吊钩升至最大高度，空载状态，以C点作为水平静位移初始点，然后将小车移动至最大幅度，吊载臂端最大额定起重量，在图4 中终止点B测得位移Δx1，则最终水平静位移为

不计风力时

此方法消除了风的影响，在任何风力状况下测得的值均一致,都是塔机无风状态下的水平位移。

5.2 方法二

同样不考虑风载荷的影响，厂家提供塔身弯曲变形趋于零时的平衡力矩，检测时加载此平衡力矩，如图1 所示，此时A点作为水平静位移初始点。然后小车移动至最大幅度，吊载臂端最大额定起重量，在B点测量出最终位移。由于塔机的平衡力矩为理论计算，会出现一定误差。

综合比较以上两种方法，方法1 可准确测得式(2)中弯矩M0产生的水平静位移ΔM0，由于检测时风压一般都较理论计算用的250Pa 风压小，即使测试也不能准确测量风载荷影响，建议厂家单独计算250Pa 风载荷产生的位移Δf，由式(4)计算出最终水平静位移。

6 结语

鉴于目前行业针对水平静位移的概念理解不一致，检测方法不统一，导致型式试验检测方法与理论概念不匹配，建议行业正式出台与理论概念匹配的水平静位移检测方法，以更好地解决设计与检测存在的不一致现象。

随着行业发展以及技术的不断进步，更高强度级别的钢材取代普通强度级别的钢材必将成为行业的发展趋势。决定塔机塔身安全的因素主要是结构的强度和稳定性，对于结构的刚度实质上仅影响到塔司的操作体验。目前塔机已全面进入变频调速控制时代，有力地提升了塔机操作的平稳性，结构刚度对于塔机结构的本质安全实际上没有任何影响，从国家标准层面如果过严限制塔身结构刚度会制约行业的发展，建议行业适当放松对塔身刚度的控制，建议塔机臂根铰点水平静位移按照≤2%H来控制，或者直接取消该限制。