不同精度INS精度分析与评估方法

王文君，柴艳菊

不同精度INS精度分析与评估方法

王文君1,2，柴艳菊1

（1. 中国科学院精密测量科学与技术创新研究院 大地测量与地球动力学国家重点实验室，武汉 430077；2. 中国科学院大学，北京 100049）

为进一步提高陀螺误差的建模精度，针对阿伦（Allan）方差仅能粗略分析陀螺的随机误差特性，而惯性导航系统的导航误差积累，可以反映惯性导航系统所有误差特性的性质，提出利用Allan方差和惯性导航系统导航误差积累2项指标，对高、中、低精度的惯性导航系统进行精度评估的方法。评估结果表明：Allan方差分析的陀螺精度与厂家的标称精度基本吻合；对于低成本惯性导航系统，导航误差积累与Allan方差分析结果不一致。分析其原因为，高精度惯性导航系统的系统性偏差相对比较稳定，在实验室条件下可以准确标定，而低成本（低精度）惯性导航系统难以准确标定；Allan方差指标作为低成本惯性导航系统精度评价指标不够合理，建议联合Allan方差和惯性导航系统导航误差积累情况综合评估INS的精度。

Allan方差；陀螺精度评估；标称精度；惯性导航系统；导航误差积累

0 引言

由于惯性导航系统（inertial navigation system, INS）的导航误差随时间快速积累，其自身难以用于导航定位，一般和其他导航手段组合使用，对其导航性能的预报主要依靠对INS传感器精度的了解[1-4]。陀螺是惯性导航系统的核心传感器，陀螺的精度决定INS的精度，因此INS的精度一般指陀螺的精度。近年来，随着微机电系统（micro-electro-mechanical system，MEMS）技术的发展，INS逐渐向小型化、低成本方向发展，目前市场上出现不同精度陀螺以满足不同用户的需求。陀螺传感器误差比较复杂，尤其是低成本的陀螺误差量级大，稳定性差，是制约INS导航精度的主要因素。如何对陀螺误差特性进行分析，给出合理的陀螺精度评估，对提高INS导航信息的预报精度具有重要意义[5-10]。

陀螺误差分为确定性误差和随机性误差[2,11-13]。确定性误差，如系统偏差、比例因子等，一般通过实验室进行标定。随机误差模型比较复杂，可能包含1种或多种随机噪声，且易受环境、运动状态等因素的影响，需要采用不同的随机模型分析方法对其进行分析和精度评估[2,4,14-18]。目前关于陀螺随机误差分析方法，比较常用的有阿伦（Allan）方差法、小波分析、功率谱、自相关分析法等[13-16]。这些方法还存在一些不足，如Allan 方差法在分析低精度陀螺观测时，存在参数估计不唯一的问题[17,19]；自相关分析法和功率谱法是频域分析法，需要长时间观测，有时观测时长甚至超过仪器寿命；功率谱分析法很难将随机误差分离出来[15]。鉴于陀螺观测具有振荡特性，且Allan方差法能够给出随机噪声特征参数[20]，计算简单易懂，虽然该方法存在不足，但是仍作为陀螺精度分析的标准方法；一般INS厂商给出的陀螺精度指标均由Allan方差分析得到，这一指标是否合理缺乏外部条件检核。

实际上，INS导航误差的积累可以直接反映INS精度。本文结合Allan方差和INS导航误差积累情况来分析不同精度INS的陀螺性能，一方面验证Allan方差分析的陀螺精度指标的合理性，另一方面，为进一步提高陀螺误差建模精度提供新的思路。

1 Allan方差计算模型

Allan方差法是由美国人David Allan于1966年提出的、用于分析原子钟振荡器稳定性的方法[18]，由于陀螺传感器本身也具有振荡器的特征，因此该方法随后被电气和电子工程师协会（The Institute of Electrical and Electronics Engineers, IEEE)作为陀螺传感器的随机误差分析的标准方法[8]。

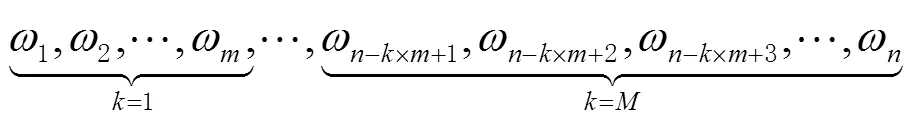
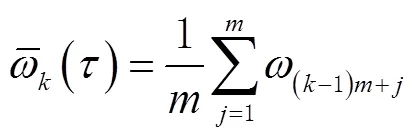
Allan方差可用于分析5种典型误差，即量化噪声、角度随机游走、零偏不稳定性、角速率随机游走和速率斜坡，其函数关系[9,14-15]为

式（3）可以简化表示为

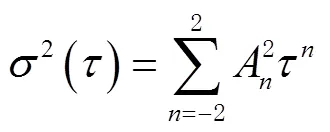
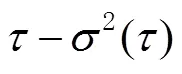
不同噪声在Allan标准差曲线中表现为不同斜率的直线，且各种类型的噪声出现在不同的相关时间区域。

其中量化噪声的曲线斜率为-1，角度随机游走的曲线斜率为-1/2，零偏不稳定性的曲线斜率为0，角速率随机游走的曲线斜率为1/2，速率斜坡的曲线斜率为1。一般曲线最低点对应的Allan标准差，即为陀螺的零偏不稳定性误差[14]。

2 INS导航解算力学编排

INS在不同坐标系中的力学编排方程在很多文献中都有详细介绍[3,24]，故不再赘述。

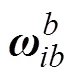
其初始对准采用全球卫星导航系统（global navigation satellite system，GNSS）在1984世界大地坐标系(world geodetic coordinate system 1984, WGS84）坐标系（系）中的定位结果，因此选取系作为INS导航坐标系不需要全球定位系统（global positioning system，GPS）导航结果的转换；另外系中INS导航方程计算简单，计算速度和精度优于其他坐标系[24]。系中INS导航解算的力学编排方程为

由式（5）通过1次积分可以得到INS的速度值，通过2次积分可以得到INS的位置值，并从姿态信息中提取出载体的姿态角。

3 实验与结果分析

3.1 数据描述

2019年5月，在武汉城区采集了车载INS数据，车上放置了高精度激光INS 1套（陀螺标称精度0.003~0.005(°)/h，采样率200 Hz）、中等精度双天线组合系统SPAN-FSAS 1套（光纤INS陀螺标称精度0.75(°)/h，采样率100 Hz）、MEMS INS2套（天璇双天线GNSS/INS系统的陀螺标称精度为10(°)/h，采样率200 Hz；多摩川INS标称精度为10~20(°)/h，采样率100 Hz）。车辆静止状态观测约20 min，实验设备安装如图1所示。通过对各INS的陀螺观测数据进行Allan方差分析和1 min单独导航位置误差积累，评估不同精度INS的陀螺性能。

图1 实验车内外设备

3.2 不同精度陀螺观测精度分析

1）Allan方差分析结果。由式（2）计算各INS陀螺观测数据的Allan标准差，结果见图2~图5。

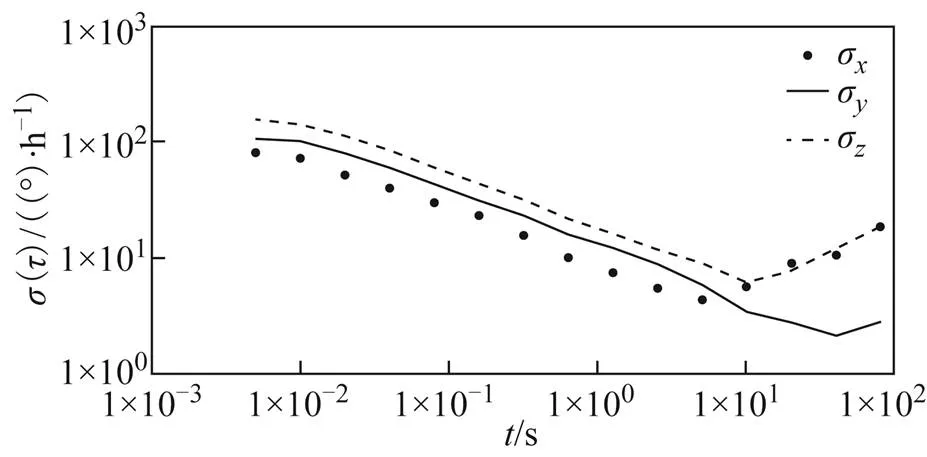
图2 天璇组合系统中陀螺Allan方差

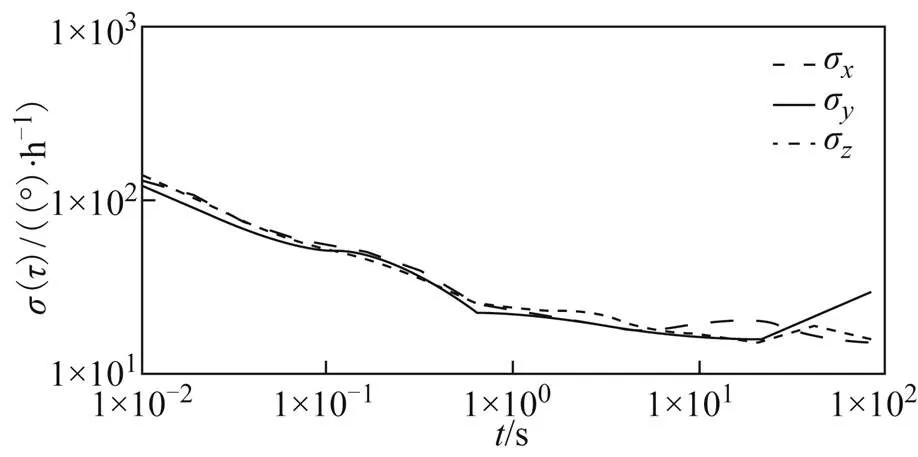
图3 多摩川INS的陀螺Allan方差

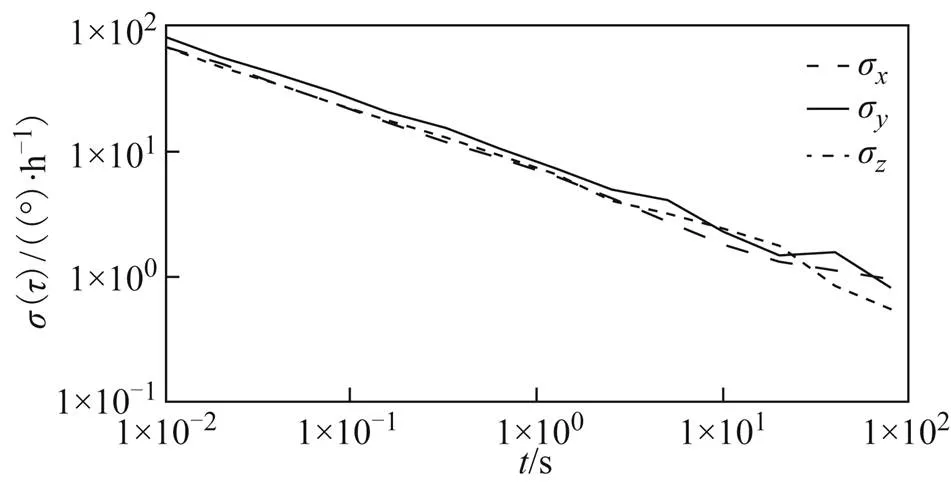
图4 SPAN-FSAS的陀螺Allan方差

图5 高精度INS的陀螺Allan方差

图2~图5中，各陀螺、、轴方向的Allan方差曲线图最低点对应的纵坐标值，即为该方向上的零偏不稳定性误差值。对由图2~图5中估计的陀螺零偏值进行整理，并和标称精度进行比较，结果如表1所示。

由图2~图5和表1结果可知：①各INS的陀螺精度水平明显不同，包含的误差种类也不同；②各INS的陀螺Allan标准差与厂家标称精度基本吻合。

由于陀螺观测精度除与本身的硬件精度有关外，还受外部观测环境的影响，Allan方差只能近似估计陀螺的精度。

2）1 min内INS位置误差积累结果。在相同观测条件下，将不同精度的INS利用GNSS定位结果进行初始对准后，根据式（5）分别进行1 min单独导航解算，位置误差的积累可以反映出INS的精度水平。位置误差积累结果如图6所示。

图6 各INS 1 min位置误差积累

由图6可知，相同观测条件下，1 min内INS位置误差积累能明显反映INS精度水平，INS精度越高，位置误差积累越慢。高精度INS的1 min内位置误差约为20 m，SPAN-FSAS的INS 1 min内位置误差约为34 m，MEMS级别的INS积累误差比较快，达到1 min内位置误差约为80 m。

综合不同精度INS的陀螺Allan方差分析结果和1 min内位置误差积累情况可知，对于MEMS 级别的INS，Allan方差分析结果中，天璇的陀螺传感器要优于多摩川的陀螺传感器，但是多摩川INS的位置误差积累要比天璇慢，这说明Allan方差在分析低精度陀螺传感器方面不完全可靠，这也可以从Allan方差计算模型来解释。分析式（2）可知，Allan方差是由前后2组观测值的均值差来计算的，显然消除了观测值的系统性误差，因此Allan仅能反映陀螺的随机误差特性，而MEMS陀螺的系统性误差很难通过前期标校进行消除的，这一误差会对INS导航解算带来比较大的影响。以上分析说明，要采用多种手段联合分析INS的精度才比较合理、可靠，尤其是对低成本陀螺传感器更是如此。

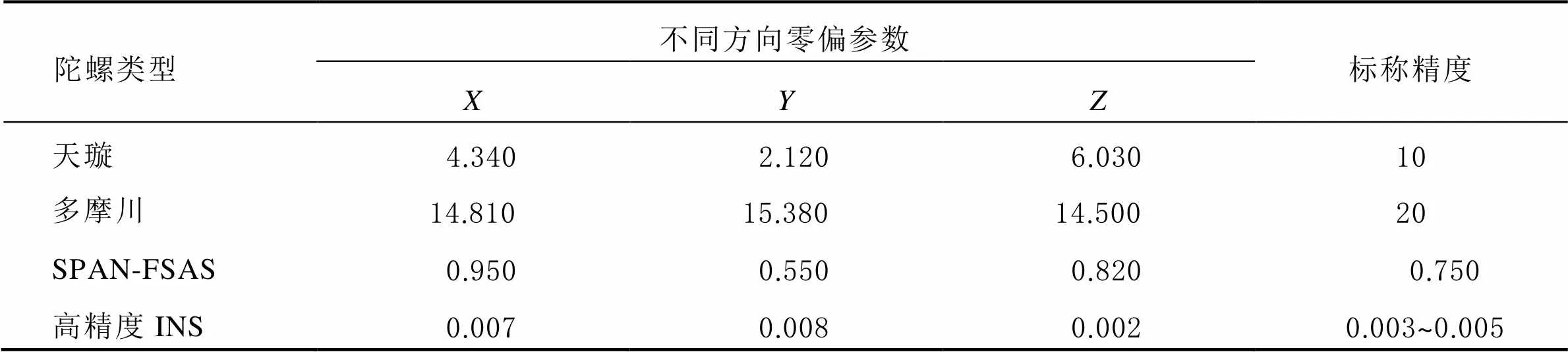
表1 由Allan方差图得到的各陀螺的零偏不稳定性结果 单位：(°)/h

4 结束语

综合以上分析，得到如下结论：

1）本文利用Allan方差及INS导航误差积累结果，对高、中、低精度INS陀螺的精度进行了评估。评估结果为：Allan方差评估的陀螺精度与厂家给定的标称精度基本一致，但是低成本INS导航误差积累与Allan方差评估精度不一致。分析其主要原因是低成本陀螺系统性误差受观测条件影响比较大，很难通过实验室条件进行准确标校，而Allan方差仅能粗略分析INS的随机误差特性。

2）影响INS导航误差积累的因素比较复杂，本文提出的综合Allan方差和INS导航误差积累评估INS的精度更合理，尤其更适合低成本INS的精度评估。

3）INS陀螺传感器误差特性受运动状态的影响比较大，也比较复杂，本文仅考虑静态陀螺观测数据，对动态条件下不同精度的INS如何进行合理的精度评估，有待进一步研究。

[1] Wu Youlong, Wang Jinling, Wang Xiaoming, et al. Stochastic modelling and estimation of inertial sensors[C]//China Satellite Navigation Conference (CSNC). Selected Paper from CSNC2014 Proceeding（Volume III）. Beijing: Springer, 2014: 499-509.

[2] 崔留争. MEMS-SINS/GPS组合导航关键技术研究[D]. 北京: 中国科学院大学, 2014.

[3] 柴艳菊. 挖掘信息提高GPS/INS导航精度的理论与方法研究[J]. 测绘学报, 2010, 39(3): 328.

[4] Ismail M , Abdelkawy E. A hybrid error modeling for MEMS IMU in integrated GPS/INS navigation system[J]. The Journal of Global Positioning Systems, 2018, 16(1): 6.

[5] 杜小菁, 曾春, 李怀建. 基于Allan方差光纤陀螺随机误差分析方法比较[J/OL]. [2019-09-28]. http: //kdoc.cnki. net/kdoc/docdown/pubdownload.aspx?dk=kdoc%3apdfdown%3a9beef7564bc386b0496bf8ba3d0e800a&lang=GB.

[6] 李晓莹, 胡敏, 张鹏, 等. 交叠式Allan方差在微机械陀螺随机误差辨识中的应用[J]. 西北工业大学学报, 2007, 25（2）: 225-229.

[7] 祝燕华, 蔡体菁, 杨卓鹏. MEMS-IMU/GPS 组合导航系统的实现[J]. 中国惯性技术学报, 2009, 17(5): 552-561.

[8] 熊必凤. 低成本MEMS陀螺仪随机漂移误差的建模及修正[D]. 重庆: 西南大学, 2017.

[9] 王辛望. 复杂环境下MEMS陀螺仪误差分析与补偿[D]. 太原: 中北大学, 2018.

[10] 杜小菁, 翟峻仪. 基于MEMS 的微型惯性导航技术综述[J]. 飞航导弹, 2014(9): 77-81.

[11] Eun-Hwan S. Accuracy improvement of low cost INS/GPS for land application[D]. Calgary: University of Calgary, 2001.

[12] 马建军, 李文强, 郑志强. MIMU随机误差分析与建模[J]. 压电与声光, 2007, 29(4): 483-486.

[13] 严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2012.

[14] Radi A, Nassar S, El-Sheimy N. Stochastic error modeling of smartphone inertial sensors for navigation in varying dynamic conditions[J]. Gyroscopy and Navigation, 2018, 9(1): 76-95.

[15] 张玉莲, 储海荣, 张宏巍, 等. MEMS 陀螺随机误差特性研究及补偿[J]. 中国光学, 2016, 9(4): 501-510.

[16] Wang Dingjie, Dong Yi, Li Qingsong, et al. Using Allan variance to improve stochastic modeling for accurate GNSS/INS integrated navigation[J/OL]. [2019-09-28]. https: //doi. org/10. 1007/s10291-018-0718-x.

[17] 吴纾婕. MIMU器件参数辨识及误差补偿技术研究[D]. 北京: 北京理工大学, 2015.

[18] 张娜, 李绪友. 动态Allan方差的理论改进及其应用研究[J]. 光学学报, 2011, 31(11): 1-6.

[19] Naser E, Hou Haiying, Niu Xiaoji. Analysis and modeling of inertial sensors using Allan variance[J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(1): 140-149.

[20] 张谦, 王玮, 王蕾, 等. 基于动态Allan 方差的光纤陀螺随机误差分析及算法改进[J]. 光学学报, 2015, 35(4): 1-7.

[21] 黎奇, 白征东, 赵思浩, 等. Allan方差方法分析环形激光陀螺仪噪声的性能评估[J]. 清华大学学报（自然科学版）, 2019, 59(11): 887-894.

[22] Qamar H A, Asif I, Farhat B, et al. Error estimation of inertial sensors using Allan variance[J]. IFAC Proceedings Volumes, 2008, 41(1): 167-171.

[23] LYU Pin, Liu Jianye, Lai Jizhou, et al. Allan variance method for gyro noise analysis using weighted least square algorithm[J]. Optik, 2015, 126(20): 2529-2534.

[24] 董绪荣, 张守信, 华仲春. GPS/INS组合导航定位及其应用[M]. 长沙: 国防科技大学出版社, 1998.

Accuracy analysis and evaluation method of INS with different precision

WANG Wenjun1,2, CHAI Yanju1

（1. State Key Laboratory of Geodesy and Earth's Dynamics, CAS Innovation Academy for Precision Measurement Science and Technology, Wuhan 430077, China;2. University of Chinese Academy of Science, Beijing 100049, China）

In order to further improve the accuracy of gyro error modelling, aiming at the characteristics that Allan variance can only roughly analyze the stochastic error characters of gyroscope, while INS navigation error accumulation can reflect the stochastic error and deterministic error characters of INS, the paper proposed to use the two indicators of Allan variance and INS navigation error accumulation to evaluate the accuracy of high, medium and low-precise INS. Results showed that the gyro accuracy with Allan variance analysis could be basically consistent with the nominal accuracy given by the manufacturer; but for low-cost INS, the analysis output of navigation error accumulation and Allan variance would not be consistent. The reason could be that the systematic deviation of high-precise INS is relatively stable and can be accurately calibrated under laboratory conditions, while it is difficult to accurately calibrate for low-cost (low-precise) INS. Furthermore, the accuracy is evaluated with only Allan variance could be not reasonable for low-cost INS, so it would be suggested that the analysis method of INS accuracy combine Allan variance and INS navigation error accumulation for more rationality and reliability.

Allan variance; gyro accuracy assessment; nominal accuracy; inertial navigation system; navigation error accumulation

P228

A

2095-4999(2020)03-0087-05

王文君, 柴艳菊. 不同精度INS精度分析与评估方法[J]. 导航定位学报, 2020, 8(3): 87-91.（WANG Wenjun, CHAI Yanju. Accuracy analysis and evaluation method of INS with different precision[J]. Journal of Navigation and Positioning, 2020, 8(3): 87-91.）

10.16547/j.cnki.10-1096.20200314.

2019-11-25

国家自然科学基金项目（41674020，41674021）；国家重点研发计划项目（2016YFB501700, 2016YFB0501900）；大地测量与地球动力学国家重点实验室项目（Y909261026）。

王文君（1994—），女，湖北武汉人，硕士研究生，研究方向为GPS / INS组合导航数据处理。

柴艳菊（1970—），女，河南商丘人，博士，副研究员，研究方向为GPS / INS精密组合导航系统理论和数据处理。