剩余地形模型及多面函数改进基准面的研究

褚永海，阮文飞，柯宝贵，汪海洪

剩余地形模型及多面函数改进基准面的研究

褚永海1,2，阮文飞1，柯宝贵3，汪海洪1,2

（1. 武汉大学 测绘学院，武汉 430079；2. 武汉大学 地球空间环境与大地测量教育部重点实验室，武汉 430079；3. 中国测绘科学研究院 大地测量与地球动力学研究所，北京 100036)

为了进一步提高高程基准面的精度，研究剩余地形模型（RTM）在近海区域高程基准面中的影响：利用陆海统一岩石等效地形（RET）构建近海区域RTM和残余高程异常；并联合多面函数拟合残余高程异常改正面，实现近海区域高程基准面模型精度的提高。实验结果表明：在近海区域，利用RTM高程异常可提高新技术改进后的欧洲地球重力联合模型（EIGEN-6C4）的精度约为3 mm；多面函数拟合后，可以将EIGEN-6C4模型的精度由9.0 cm提高到3.4 cm。

高程异常；剩余地形模型；岩石等效地形；多面函数；高程基准

0 引言

在区域高程基准面确定中，地形数据主要用于高频信息的获取。处理地形数据通常有4种策略：①考虑整个地形的影响，包括布格改正和地形改正；②只考虑局部地形影响；③对地形进行均衡归算，有艾里-海斯卡涅以及普拉特-海福德模型[1-2]；④使用剩余地形模型（residual terrain model, RTM）[3]。

RTM的主要思想是用1个真实地形减去1个参考地形得到剩余地形，然后再计算剩余地形的影响[3]。本质上来说，RTM将参考面以上的地形质量移去，而参考面以下质量亏损部分将被填充。在物理大地测量学中的短尺度重力建模[4]或高频重力正演[5]中，经常使用RTM。此外，还利用RTM来改善全球引力场模型（global geopotential model, GGM）计算的高程基准面。例如文献[6-7]联合地球引力模型2008（Earth gravitational model 2008, EGM2008）和数字地面模型2006.0（digital terrain model 2006.0, DTM2006.0），来改善重力数据稀少的山地区域似大地水准面，精度可以提高2 cm，这主要是考虑山区重力数据稀少，而且直接使用的高阶GGM也没有完全包含地球重力场的高频信息，所产生的截断误差在山区对高程异常的影响可以达到10 cm量级。利用RTM可以对截断误差进行估计并有效改善GGM[8]。这种思想也被国内学者用于区域基准面的改进。例如：文献[9]在华南地区选择了1个带状和1个面状区域，利用RTM模型来改进EGM2008；文献[10]在广东省及周边区域对RTM高程异常的精度进行了数值计算与分析；文献[11]将RTM用于改进长江南京段的高程控制。

针对近海区域区域高程基准面确定中RTM的贡献及影响，本文利用30″和15″分辨率陆地高程和海洋深度模型（SRTM30_PLUS和SRTM15_PLUS）[12]、岩石等效球谐地形模型2012(rock-equivalent terrain 2012, RET2012)[13]、欧洲地球重力场联合模型（European improved gravity model of the earth by new techniques, EIGEN-6C4）[14]、全球定位系统（global positioning system，GPS）及水准测量数据，分析RTM对EIGEN-6C4模型的改善情况。同时，采用多面函数法对残余高程异常进行拟合，再联合GGM高程异常、RTM高程异常，恢复得到近海区域高程基准面，并用独立GPS/水准测量数据进行检核。

1 原理方法

1.1 剩余地形建模

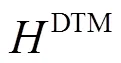
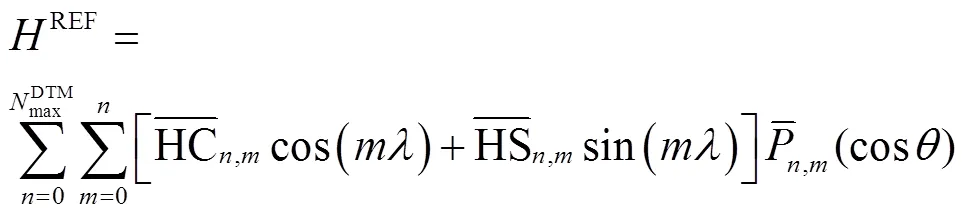
1.2 高程异常

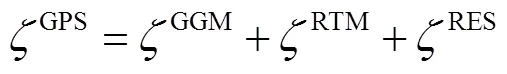
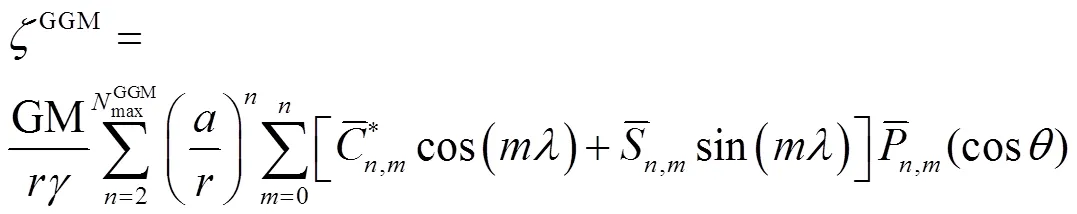
式中：G为万有引力常数；ρ为长方体的密度；为长方体顶点坐标；l为距离，用坐标表示成。长方体顶点E的坐标可以用表示；顶点K的坐标用表示，其他点都可以用点E和点K的坐标表示，具体位置关系参见图1。

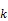
根据布隆斯（Bruns）公式，每个长方体地形引力位对高程异常的贡献[15]表示成

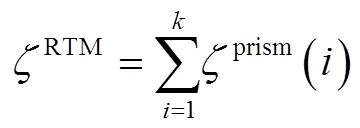
1.3 残余高程异常及多面函数拟合

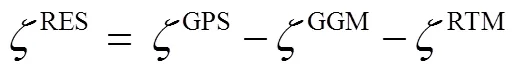
在重力场参量的拟合计算中，广泛使用多面函数，它的基本思想是，任何1个规则或不规则的连续曲面均可以由若干简单面来叠加逼近。具体做法是：在每个数据点上建立1个曲面，然后将各个旋转曲面按一定比例叠加成一张整体的连续曲面，使之严格地通过各个数据点。其函数模型[17]可以表示成

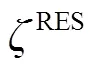
2 实验与结果分析

2.1 研究区域和使用数据

当前高精度、高分辨的全球陆地地形数据主要有3″分辨率的SRTM地形数据，海域数据除了少数船测数据之外，主要是依据卫星测高反演海域重力异常而获得海底地形[18]。将陆地SRTM和海洋深度模型融合后，国外先后发布了包含陆地地形及海底地形，分辨率为30″的SRTM30_PLUS模型及分辨率为15″的SRTM15_PLUS模型。其中SRTM15_PLUS（如图2所示）在研究范围（115°E~125°E，31°N~41°N）的统计信息如表1所示，最低点的高度-128.2 m，位于（122°13′30″E，38°50′15″N），最高点的高度2770.0 m，位于（115°02′30″E，39°56′30″N）。利用海域部分基于岩石等效地形的概念[8,19]，利用海水进行压缩，构建密度均匀（岩石密度2670 kg·m-3）的岩石等效地形，相应的数值结果列于表1。

表1 地形模型高度值统计 单位：m

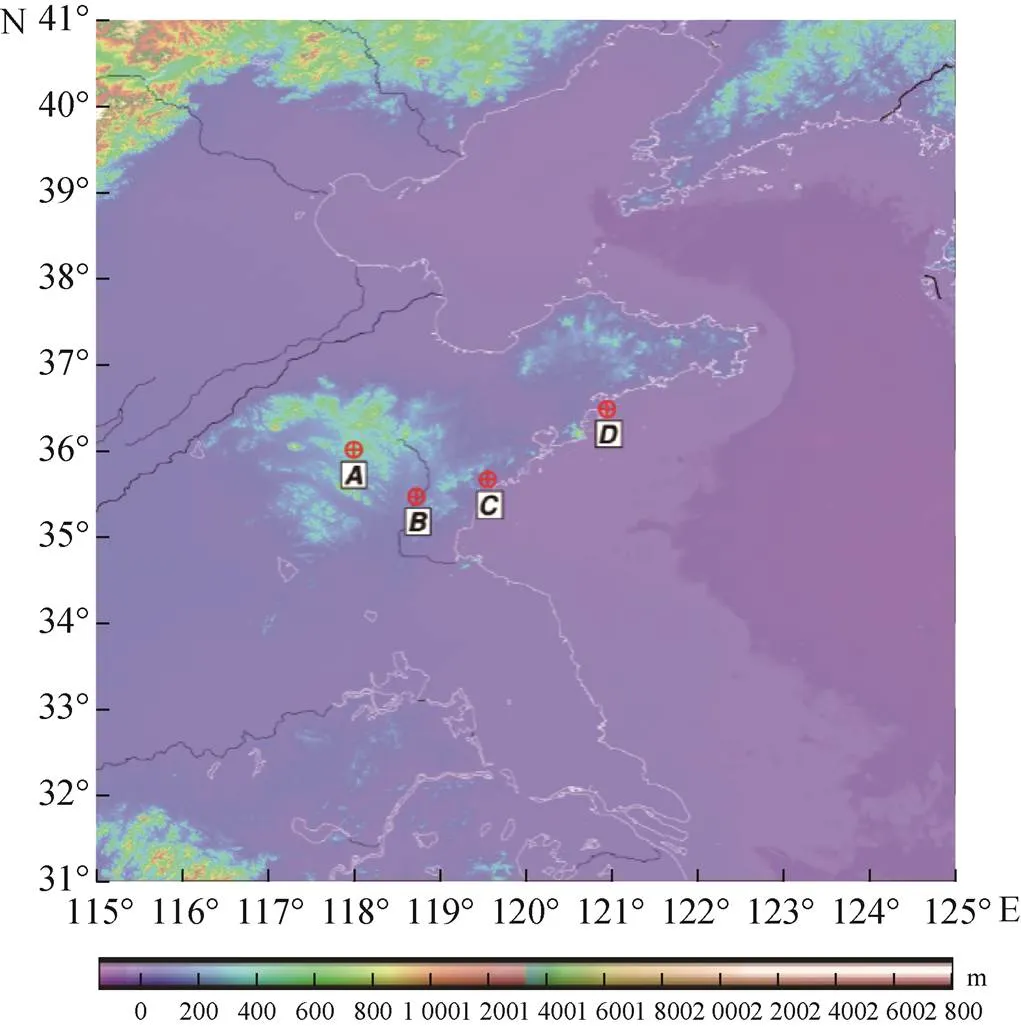
图2 SRTM15_PLUS陆地地形/海洋深度模型

基于SRTM30_PLUS，利用球谐分析确定了全球地形及引力位的球谐模型2012和2014[13,20]，其中包含岩石等效球谐地形模型（RET2012和RET2014）。RET2012模型的阶数为2160阶，相当于5′分辨率，与EGM2008、EIGEN_6C4阶次相同。RET2012按15″分辨率计算的球谐地形，在研究区域内最大值高度约为2234.1 m，最小值为-67.6 m，平均高度为57.2 m（见表1）。

选取SRTM15_PLUS岩石等效地形作为真实地形模型，参考地形使用RET2012岩石等效球谐地形，2者相减得到RTM模型。RTM模型在研究区域最大值高度约为851.4 m，最小值高度约为-684.2 m，平均值高度约为-0.3 m（见表1）。

此外，将GPS/水准点共计152个分为2组：第1组作为多面函数拟合计算点（如图3所示），共计88个；第2组为检核点（如图4所示），共计64个点，用来对拟合改正面进行独立检核。

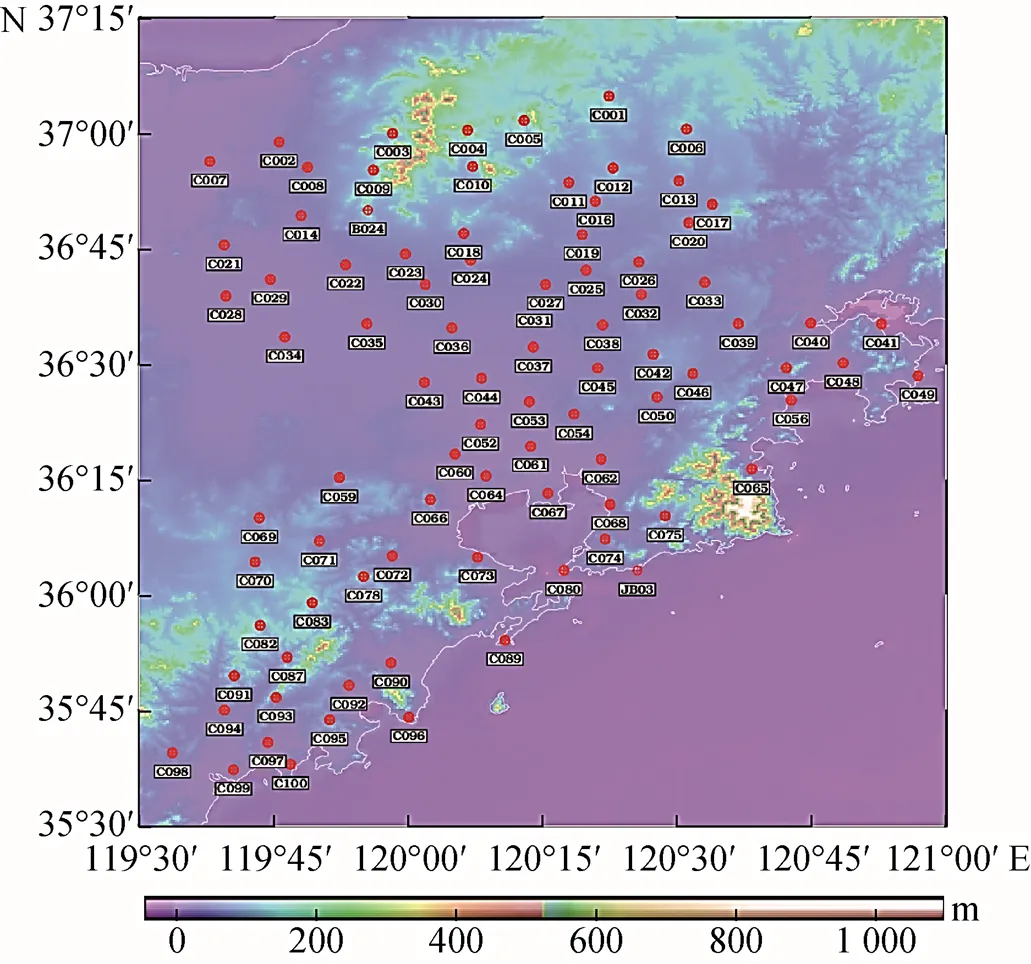
图3 拟合GPS水准点分布

图4 检核GPS水准点分布

2.2 积分半径对RTM高程异常的影响

为了解长方体模型积分半径的选取情况，选取4个点、、和进行测试（如图2所示）。4个点的海拔高程分别约为382.0、103.6、38.3和78.6 m。其中点位于山区，点位于二山中间，和点均在近海附近。此外，4个点的剩余地形分别约为-77.3、-8.4、25.3和-6.8 m。从剩余地形来看，除了点高于参考面之外，其他3个点都低于参考面。不分内区和外区，数据分辨率取7.5″，积分半径取0.1、0.2、0.5、1、2、3、4、5、10、15、…、300 km后分别进行计算。

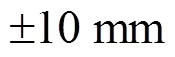
为了进一步说明积分半径的影响，以积分半径40、60、…、300 km计算了152个GPS水准点上的RTM高程异常，其统计结果列于表2。从极值可以看出，RTM对高程异常的影响为-4.6~1.7 cm。由于构建剩余地形的初衷之一是剩余量的平均值趋近于零，因此积分半径取240 km比较合适。

图5 RTM高程异常与积分半径的关系

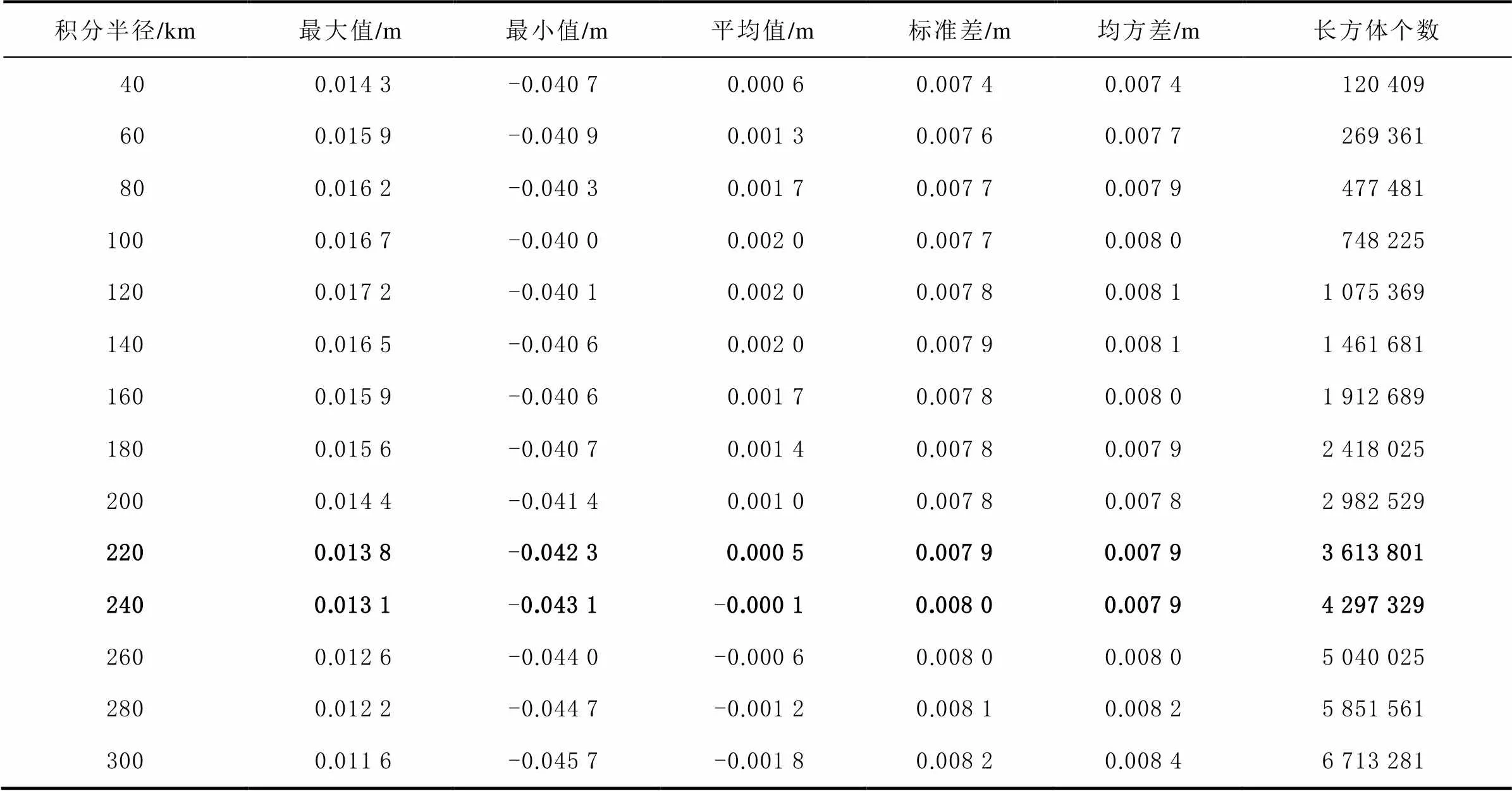
表2 不同积分半径下RTM高程异常统计

2.3 RTM高程异常及残余高程异常拟合

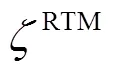
图6 RTM高程异常分布

图7 多面函数法拟合残余高程异常

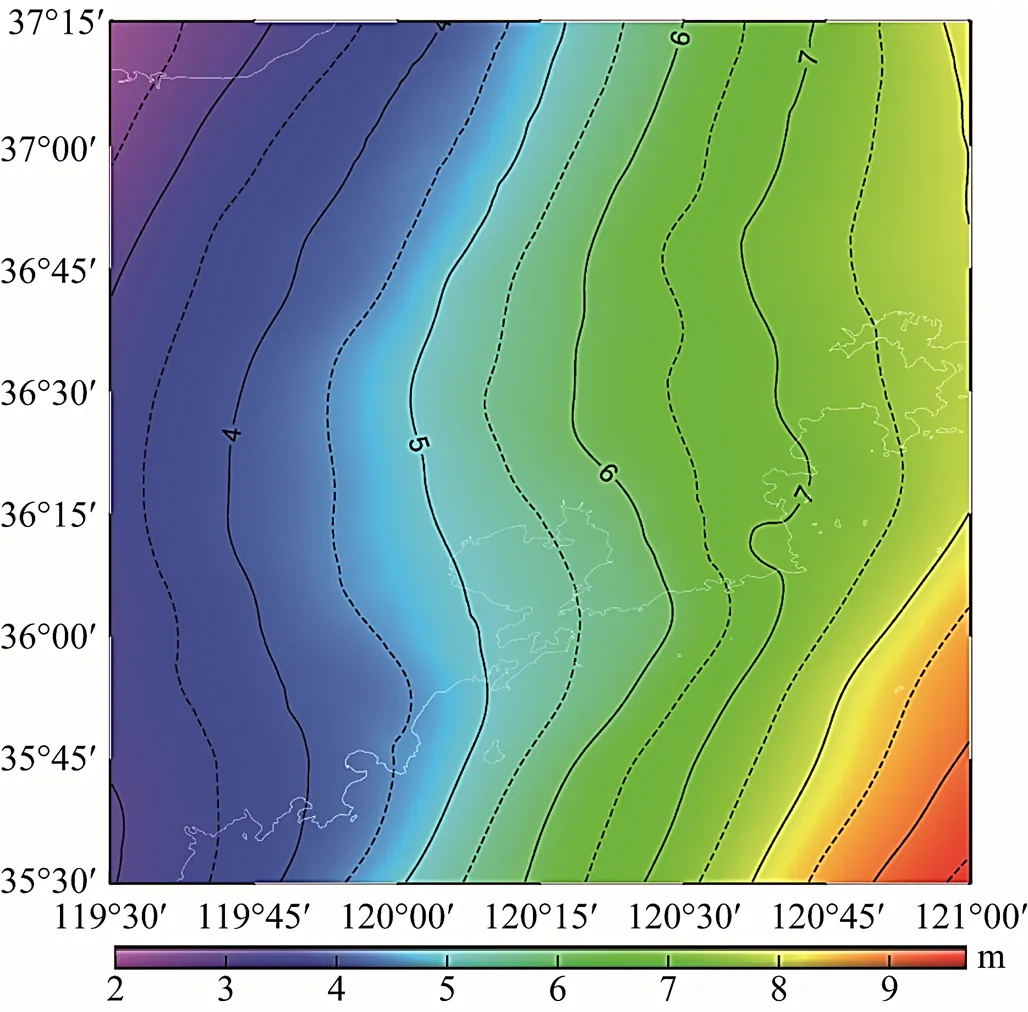
图8 拟合改正后的高程基准面

2.4 精度检核

重力模型高程异常顾及剩余地形影响，并利用GPS/水准拟合改正得到的区域高程基准面，除了海域无GPS/水准控制存在局部扭曲之外，其他区域的精度可以用另一组64个GPS/水准数据（如图4所示）进行外部检核。为了比较RTM高程异常改正、残余地形拟合改正对高程基准面的贡献，进行了以下精度估计。

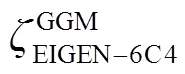
在顾及RTM高程异常的基础上，如果再顾及残余高程异常改正，即利用GPS/水准数据检核拟合后的基准面（见图8），高程异常差值统计列于表3中的最后3行。其中，由于拟合残余高程异常改正面使用的是88个拟合点，多面函数法拟合的曲面通过拟合点，因此，这组GPS/水准点检核统计数值均为零，即内符合检核无误差。而使用未参与拟合的64个GPS/水准数据检核，最大差值为0.0666 m，最小值为-0.1051 m，平均差异为-0.0015 m，标准差为0.0341 m，均方差为0.0339 m。说明了外符合检核精度约为3.4 cm。如果使用全部152个点检核，精度约为2.2 cm。

表3 EIGEN-6C4/RTM高程异常与GPS/水准高程异常比较

续表3

3 结束语

剩余地形模型在高海拔地形起伏地区，特别是在无实测重力地区，能够有效地改善全球重力场模型短波分量因模型截断的影响[7,9-11]；在近海地区，剩余地形模型对高程异常的改进可提高的精度约为6.5 mm[8]。为了分析剩余地形模型在中国近海的应用情况，选取青岛及周边区域进行计算分析，包括数值积分半径的选取、剩余地形模型的贡献、拟合改正后的精度情况等，数值结果表明：

剩余地形模型对重力场模型短波分量的改善，不仅可以用于高程异常的改善，也可以用于重力、垂线偏差的改善[8]，这对于无实测重力数据地区重力场模型的构建，具有重要的作用。近几十年来，RTM技术已经被广泛用于大地测量领域，但以目前的方式使用时，还有一些问题需要解决：例如，计算点位于较低的山谷时，为了保证引力位的调和性，需要进行调和改正；当数值积分半径较大时，需要顾及地球曲率的影响。另外，在残余地形拟合改正面中，海域因无GPS/水准约束出现扭曲，这可以将海面地形作为“虚拟”GPS/水准点，以保证将陆地高程传递到海域范围。总之，如果在RTM建模中进行调和改正和地球曲率改正，在拟合曲面时对海洋进行约束，可以进一步提高程基准面的精度，并且实现陆海高程基准的统一。

[1] HEISKANEN W A, MORITZ H. Physical Geodesy[M]. New York: Freeman W. H, 1967: 364.

[2] HOFMANN-WELLENHOF B, MORITZ H. Physical Geodesy[M]. Austria: Springer-Verlag Wien, 2006: 403.

[3] FORSBERG R. A study of terrain corrections, density anomalies and geophysical inversion methods in gravity field modelling, 355[EB/OL].[2019-12-28].https://apps.dtic.mil/dtic/tr/fulltext/u2/a150788.pdf.

[4] HIRT C, BUCHA B, YANG M, et al. A numerical study of residual terrain modelling (RTM) techniques and the harmonic correction using ultra-high-degree spectral gravity modelling[J]. Journal of Geodesy, 2019, 93(9): 1469-1486.

[5] REXER M, HIRT C, BUCHA B, et al. Solution to the spectral filter problem of residual terrain modelling (RTM)[J]. Journal of Geodesy, 2018, 92(6): 675-690.

[6] PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the Earth gravitational model 2008 (EGM2008)[J]. Journal of Geophysical Research, 2012, 117(B04): 1-38.

[7] HIRT C, FEATHERSTONE W E, MARTI U. Combining EGM2008 and SRTM/DTM2006.0 residual terrain model data to improve quasigeoid computations in mountainous areas devoid of gravity data[J]. Journal of Geodesy, 2010, 88(9): 557-567.

[8] HIRT C. RTM gravity forward-modeling using topography/bathymetry data to improve high-degree global geopotential models in the coastal zone[J]. Marine Geodesy, 2013, 36(2): 1-20.

[9] 张兴福, 刘成. 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J].测绘学报, 2012, 41(1): 25-32.

[10] 张永毅, 张兴福, 周波阳, 等.剩余地形模型高程异常计算的积分法及精度分析[J].大地测量与地球动力学, 2016, 36(9): 770-774.

[11] 翟长治, 姚宜斌, 岳顺.基于EGM2008和剩余地形模型的区域似大地水准面精化方法[J]. 大地测量与地球动力学, 2015, 35(6): 941-944.

[12] BECKER J J, SANDWELL D T, SMITH W H F, et al. Global bathymetry and elevation data at 30 arc seconds resolution: SRTM30_PLUS[J]. Marine Geodesy, 2009, 32(4): 355-371.

[13] HIRT C, KUHN M. Evaluation of high-degree series expansions of the topographic potential to higher-order powers[J]. Journal of Geophysical Research: Solid Earth, 2012, 17(B12): 1-12.

[14] FÖRSTE C, BRUINSMA S L, ABRIKOSOV O, et al. EIGEN-6C4: the latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse[EB/OL]. [2019-08-15]. http: //icgem. gfz-potsdam. de/Foerste-et-al-EIGEN-6C4. pdf.

[15] HIRT C. Prediction of vertical deflections from high-degree spherical harmonic synthesis and residual terrain model data[J]. Journal of Geodesy, 2010, 84(3): 179-190.

[16] NAGY D, PAPP G, BENEDEK J. The gravitational potential and its derivatives for the prism[J]. Journal of Geodesy, 2000, 74(7/8): 552-560.

[17] HARDY R L. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research, 1971, 76(8): 1905-1915.

[18] SANDWELL D T, MÜLLER R D, SMITH W H F, et al. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure[J]. Science, 2014, 346(6205): 65-67.

[19] KUHN M, HIRT C. Topographic gravitational potential up to second-order derivatives: an examination of approximation errors caused by rock-equivalent topography (RET)[J]. Journal of Geodesy, 2016, 90(9): 883-902.

[20] HIRT C, REXER M. Earth2014: 1 arc-min shape, topography, bedrock and ice-sheet models-available as gridded data and degree-10, 800 spherical harmonics[J]. International Journal of Applied Earth Observation and Geoinformation, 2015, 39: 103-112.

[21] 李建成, 褚永海, 徐新禹.区域与全球高程基准差异的确定[J].测绘学报, 2017, 46(10): 1262-1273.

Research on improved datum surface of residual terrain model and polyhedral function

CHU Yonghai1,2, Van Phi NGUYEN1, KE Baogui3, WANG Haihong1,2

（1. Schoolof Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China; 3. Institute of Geodesy and Geodynamic, Chinese Academy of Surveying and Mapping, Beijing 100036, China）

In order to further improve the accuracy of height datum, the paper studied on the effect of RTM in the determination of local height datum in offshore area: the land and sea unified rock-equivalent topography was used to establish the offshore area RTM and residual height anomaly, and the corrected surface of residual height anomaly was fitted by combining a polyhedral function to improve the accuracy of height datum surface model in offshore area. Experimental result showed that: in the offshore area, RTM height anomaly could help improve the accuracy of EIGEN-6C4 by about 3 mm; moreover, the accuracy of the EIGEN-6C4 model could be improved from 9.0 cm to 3.4 cm after the polyhedral function fitting.

height anomaly; residual terrain model(RTM); rock-equivalent terrain(RET); polyhedral function; height datum

P228

A

2095-4999(2020)03-0007-08

褚永海，阮文飞，柯宝贵，等. 剩余地形模型及多面函数改进基准面的研究[J]. 导航定位学报, 2020,8(3): 7-14.（CHU Yonghai, Van Phi NGUYEN, KE Baogui, et al. Research on improved datum surface of residual terrain model and polyhedral function[J]. Journal of Navigation and Positioning, 2020, 8(3): 7-14.）

10.16547/j.cnki.10-1096.20200302.

2020-01-08

国家重点研发计划项目（2016YFB0501702）；国家自然科学基金项目（41774010, 41974016）。

褚永海（1976—），男，贵州普定人，博士，副教授，硕士研究生导师，研究方向为卫星测高技术应用、高程基准确定等。