扭王字块体护面斜坡堤胸墙受力试验研究

孙大鹏，刘 飞，修富义，王 键，董 胜

(1.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116024; 2.亿达中国控股有限公司，辽宁 大连 116024; 3.中交第一航务工程勘察设计院有限公司，天津 300222; 4.中国海洋大学 工程学院，山东 青岛 266100)

在斜坡堤设计时，通常会采用人工块体护面、消浪，并在堤顶设置胸墙。斜坡堤胸墙的安全情况，对斜坡堤掩护的后方水域稳定性产生了直接影响，进而影响到结构物的安全与作业人员的生命财产安全。众多学者就胸墙型式、计算方法等方面对胸墙受力展开了深入地研究。李雪艳等[1]在物理模型试验中设计了不同结构型式的胸墙，探求胸墙水平波浪力的变化规律；王登婷[2]、吴苏舒和张玮[3]设计物模断面试验，分别从受力的角度和越浪量的角度对斜坡堤弧形胸墙与直立胸墙作出比较；李玉龙[4]通过波浪水槽试验得出斜坡堤掩护程度越好，胸墙所受波压力越小的结论。而对于堤面放置块体的斜坡堤直立胸墙的水平波浪力，在《港口与航道水文规范》[5]与《防波堤设计与施工规范》[6]中虽规定了计算方法，但该方法并未对人工块体进行分类。潘少华[7]、苏伟东[8]设计了相关物模断面试验，总结了斜坡堤分别在扭工字块体、四角锥体、普通方块护面结构形式下，胸墙水平波浪力试验值与规范计算值有较大差别，但试验未讨论扭王字块体护面结构形式；琚烈红[9]结合物模试验分析在规则波作用下，扭王字块体护面斜坡堤胸墙水平波浪力与波高、波陡的关系；杨洪旗等[10]依据现有工程，分析在不规则波作用下肩宽对斜坡堤在扭王字块体掩护条件下胸墙水平波浪力的影响，但并未给出斜坡堤在扭王字块体掩护条件下胸墙水平波浪力的计算关系式。

在斜坡堤的设计中，扭王字块体的应用范围十分广泛。而依据水动力条件和断面结构研究不规则波和扭王字块体护面斜坡堤的相互作用的系统、全面的文献成果，迄今尚鲜见报导。孙大鹏等[11]籍助物理模型试验提出了不规则波作用下扭王字块体护面斜坡堤越浪量的计算公式。下文进一步给出了不规则波作用下扭王字块体护面斜坡堤胸墙水平波浪力的计算公式，系统性地丰富了斜坡堤在扭王字块体掩护条件下的研究范畴。本成果对斜坡堤工程设计具有一定的借鉴意义。

1 试验概况

1.1 试验条件

物理模型试验在尺寸50 m×3 m×1 m(长×宽×高)的造波水槽中开展，造波区域采用液压伺服造波系统，可以产生稳定的不规则波。为了使试验断面前的波浪更加均匀，沿宽度方向将水槽分隔为宽2.2 m和0.8 m两部分，模型布置在宽0.8 m的一侧，将消能网缓坡铺设在水槽末端用于消波，模型的位置如图1所示。物理模型试验采用波谱为JONSWAP谱的不规则波(γ=3.3)。

图1 模型位置示意

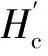
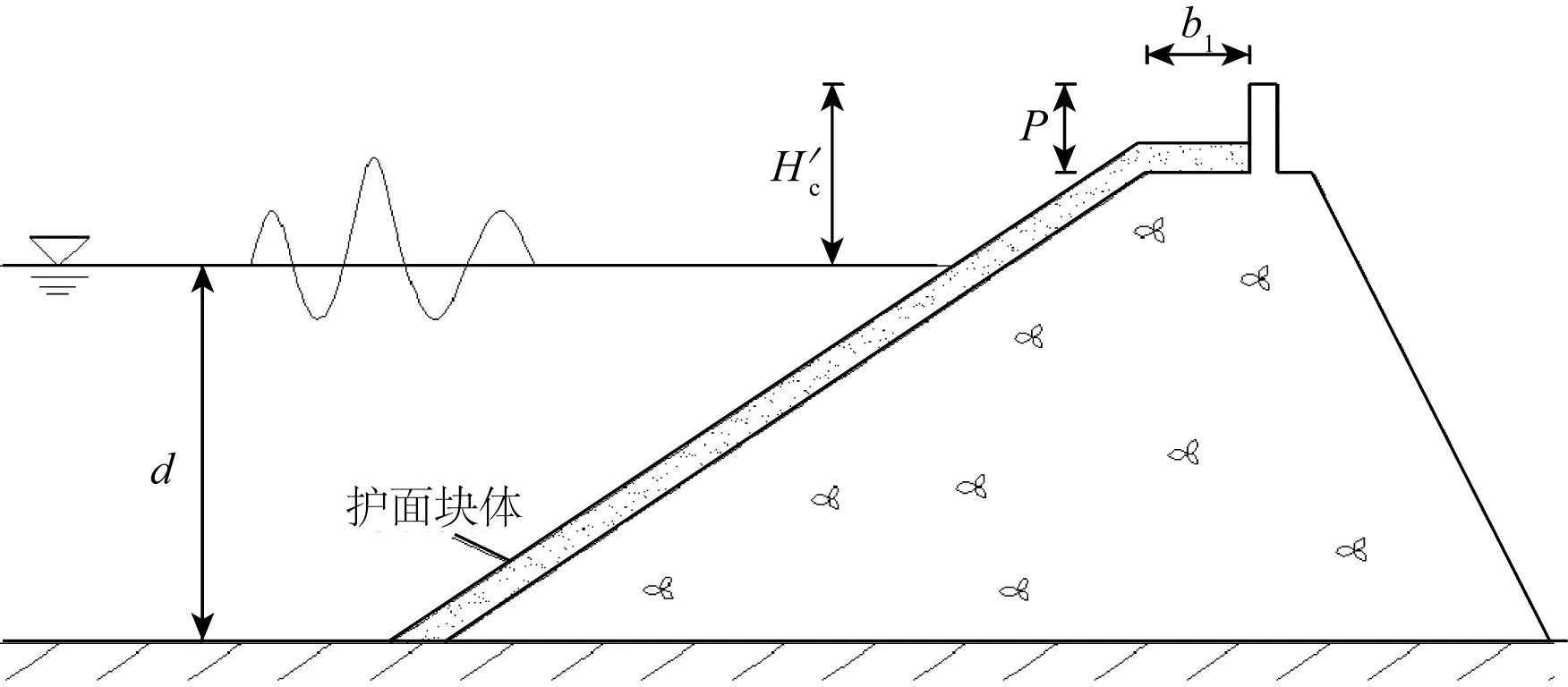
图2 斜坡堤断面

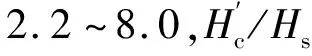
试验开展前，通过对未放置模型的空水槽凑浪试验得到试验目标波浪，16种工况如表1所示。试验开始进行后，应用表1中16种工况组合进行五组试验，先开展斜坡堤在混凝土板护面条件下的胸墙水平波浪力试验，再依次进行扭王字块体尺寸h为4.2 cm、6.0 cm、6.5 cm和7.8 cm的扭王字块体护面斜坡堤胸墙水平波浪力试验。试验采用有机玻璃板模拟胸墙，通过在有机玻璃板上钻孔安装点压传感器测量胸墙受力。通过改变有机玻璃板的位置、高度，改变水位、波况、块体尺寸等变量开展试验。试验共计组次80组，每组工况试验次数超过3次，保证每组工况的试验数据都具有较好的重复性。

图4 图4 扭王字块体尺寸

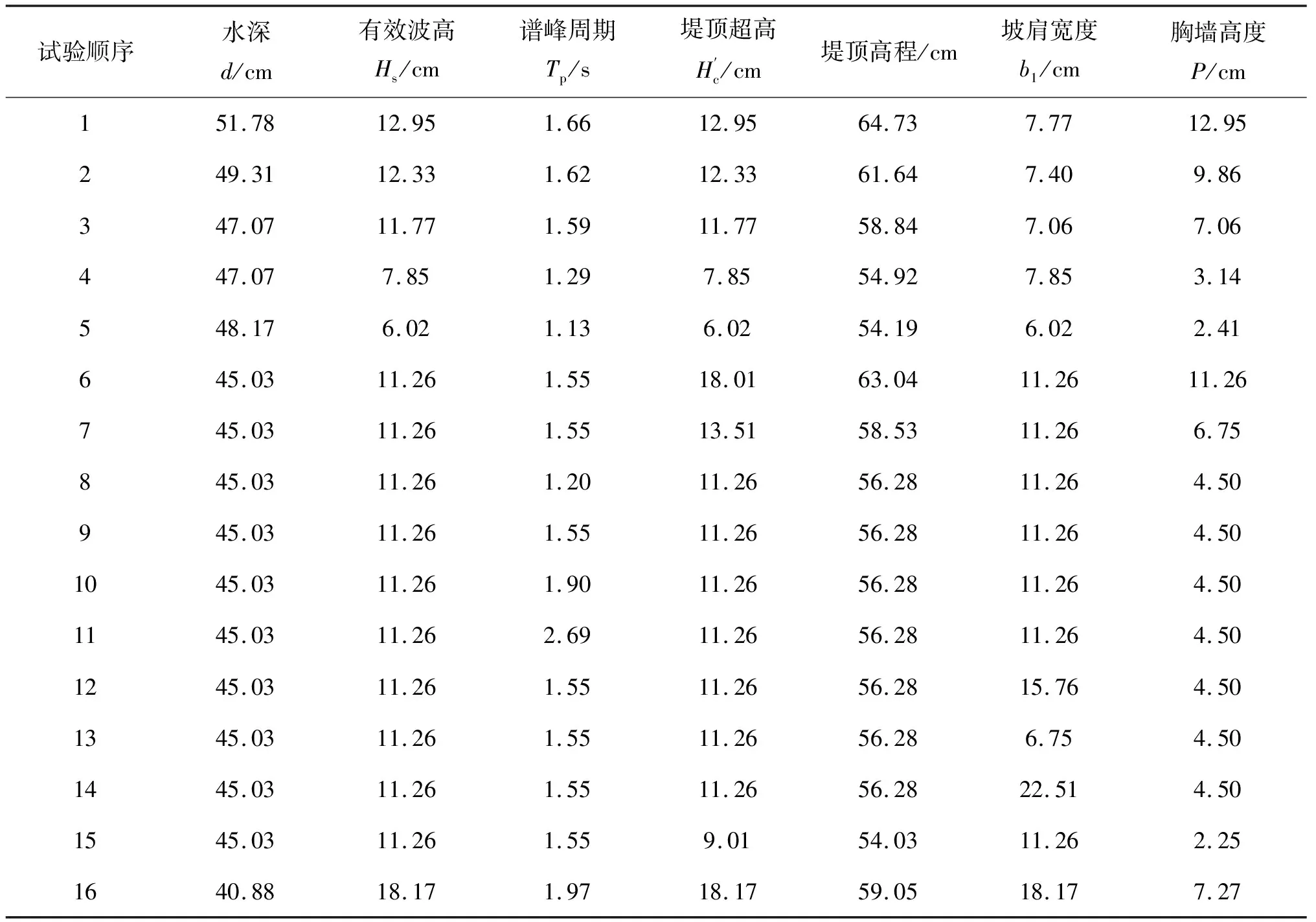
表1 试验工况组合

根据Goda[12]提出的破波指标的计算方法以及Kamphuis[13]对不规则波破波指标的修正，结合物理模型试验现象，在表1所示的16种工况中，仅第16种工况对应的波浪出现破碎现象，其余均未破碎。

1.2 试验数据采集及处理

物理模型试验中，为保证每组试验中不规则波的波数大于100个，不规则波的造波时长分为两种：一种为164 s(Tp<2.0 s)，另一种为328 s(Tp﹥2.0 s)。在胸墙上安装点压力传感器，传感器接收信号面设置在迎浪面处，测量每组工况的波浪压强，通过有效控制面积积分计算单宽胸墙水平波浪力。采样频率100 Hz，得到不同测点压强的时间过程线，积分计算得到每组试验波峰作用时胸墙水平波浪力(取时间历程上水平总力的最大值作为试验分析值)。得到试验数据分析值后，采用物理量的无因次化以及单一变量分析方法，找到相关物理量的变化规律，运用多元回归方法拟合多因素影响下胸墙水平波浪力的计算公式，并验证公式的精确性与适用性。使用前点压力计经过反复测试，性能稳定，可以应用于试验。如表1所示，试验中共设计胸墙高度10种，点压力计平均控制高度为10 mm，当胸墙高度为129.5 mm时，胸墙点压力计位置分布规则如图5所示。

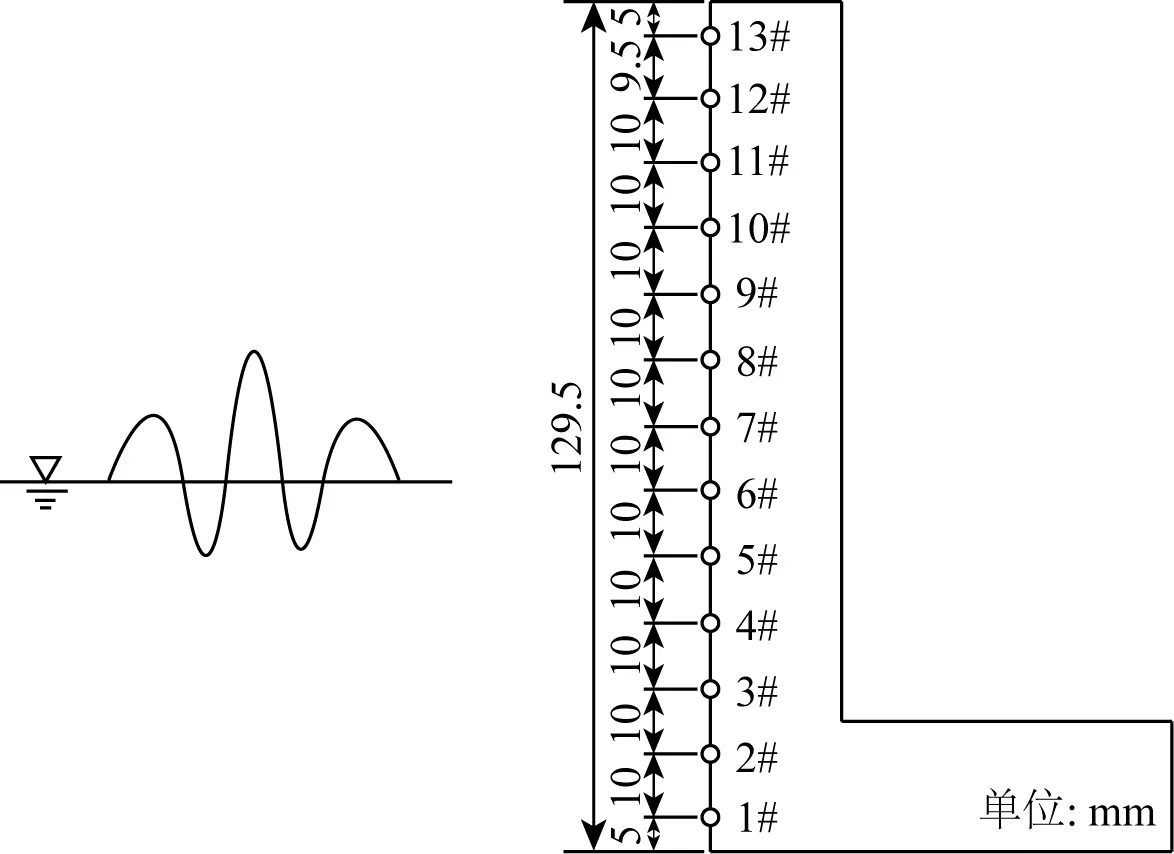
图5 胸墙测点布置

2 斜坡堤在混凝土板护面条件下胸墙水平波浪力的影响因素分析

现行《港口与航道水文规范》[5]中以混凝土板护面斜坡堤胸墙水平波浪力为基准，当斜坡堤上有块体护面时，《防波堤设计与施工规范》[6]表明，作用在胸墙上的水平波浪力可用斜坡堤在混凝土板护面条件下胸墙水平波浪力乘以折减系数0.6～0.7的方法计算。

循规范中斜坡堤在有块体护面条件下胸墙水平波浪力的计算以混凝土板护面条件下胸墙水平波浪力为计算基准的编制思路，试验首先进行混凝土板护面斜坡堤胸墙受力的试验研究。结合试验结果分析了斜坡堤在混凝土板护面条件下胸墙水平波浪力与波陡等五种影响因素的相关关系，采用单一变量分析与非线性拟合等方法，遵循π定理，最终得到斜坡堤在混凝土板护面条件下胸墙水平波浪力的无因次表达式：

(1)

式中：F板表示斜坡堤在混凝土板护面条件下的单宽胸墙水平波浪力，N/m；ρ表示水的密度，kg/m3；Hs表示有效波高，m；L表示谱峰周期计算的波长，m。

2.1 单一变量分析Hs/L

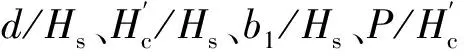
2.2 单一变量分析d/Hs

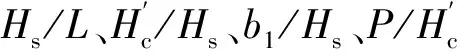
图6 F板/(ρgHs2)与Hs/L关系

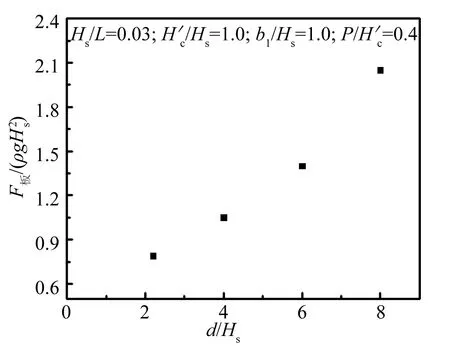
图7 F板/(ρgHs2)与d/Hs的关系

2.3 单一变量分析

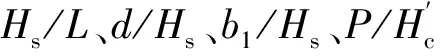
2.4 单一变量分析b1/Hs

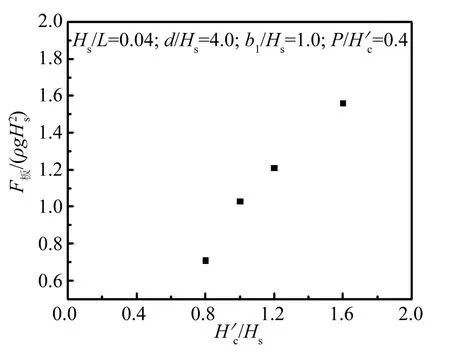
图8 F板/(ρgHs2)与的关系

图9 F板/(ρgHs2)与b1/Hs关系

2.5 单一变量分析

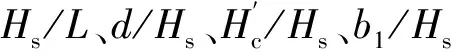
2.6 斜坡堤在混凝土板护面条件下胸墙水平波浪力无因次计算表达式

(2)

上式相关系数R>0.90，满足非线性拟合要求。规范方法计算值和式(2)计算值与物模试验值的比较如图11所示(规范采用平均压强方法计算，波高取为H1%，周期取为谱峰周期)。如图11所示，式(2)的计算值与物模值对应的点在直线y=x两侧均匀分布，式(2)计算值与物模试验值有较高的匹配度。

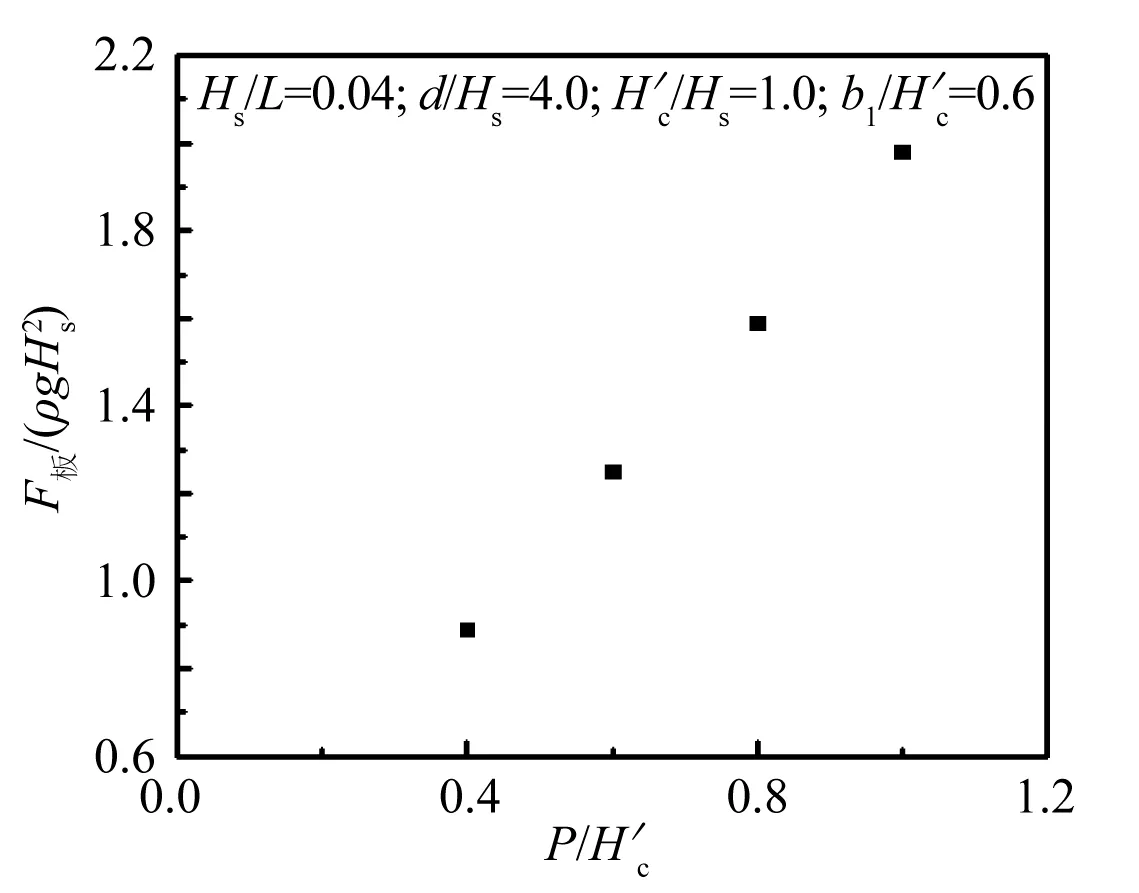
图10 F板/(ρgHs2)与的关系

图11 F板/(ρgHs2)计算值与试验值对比

3 扭王字块体护面斜坡堤胸墙水平波浪力折减系数的影响因素分析

综合考虑波陡等六种影响因素，采用单一变量分析与非线性拟合等方法，遵循π定理，最终确定扭王字块体护面斜坡堤胸墙水平波浪力折减系数的无因次计算关系式：

(3)

(4)

式中：K表示扭王字块体护面斜坡堤胸墙水平波浪力折减系数，是同一工况下，扭王字块体护面斜坡堤胸墙水平波浪力F(N/m)与斜坡堤在混凝土板护面条件下胸墙水平波浪力F板的比值。

3.1 单一变量分析Hs/L

3.2 单一变量分d/Hs

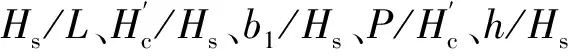
图12 K与Hs/L的关系

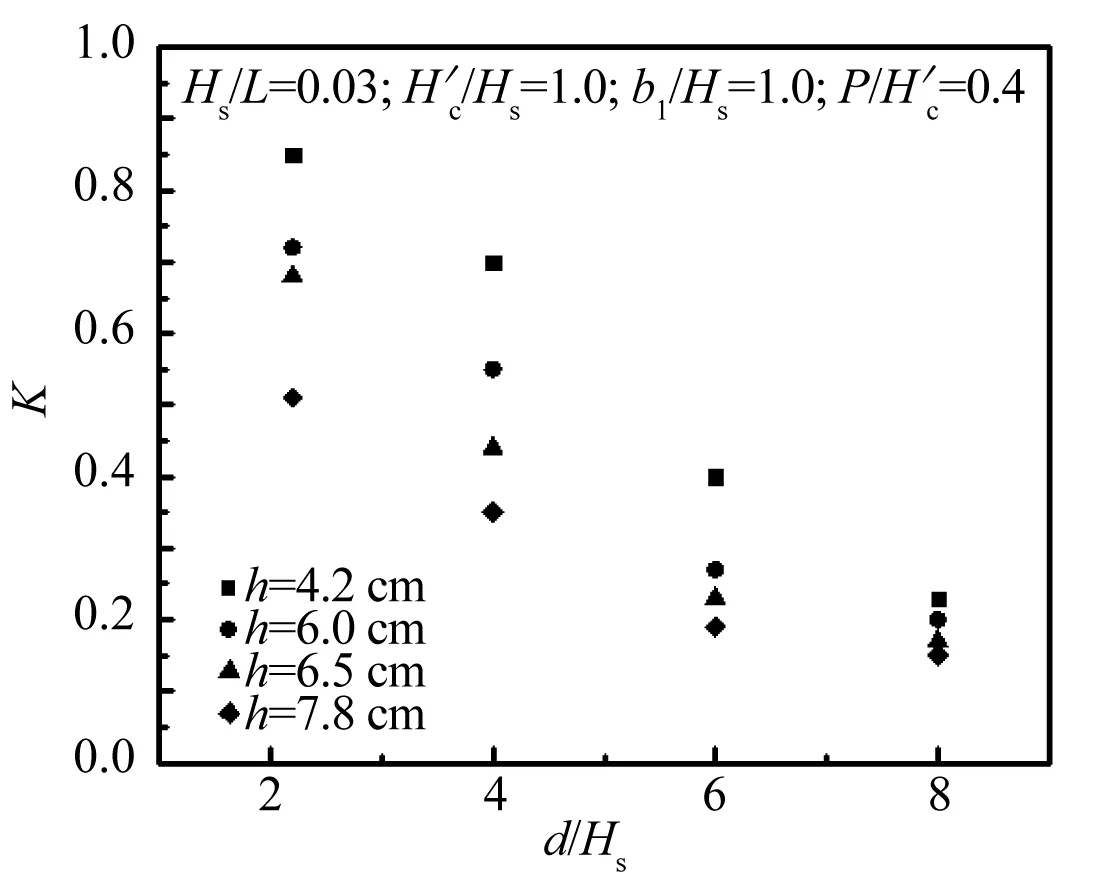
图13 K与d/Hs的关系

3.3 单一变量分析

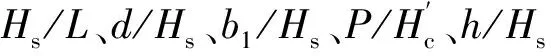
3.4 单一变量分析b1/Hs

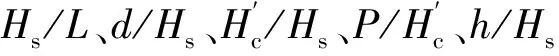
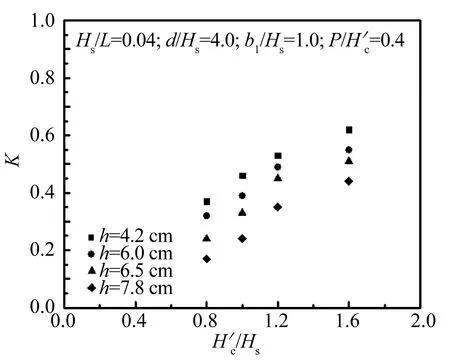
图14 K与的关系

图15 K与b1/Hs的关系

3.5 单一变量分析

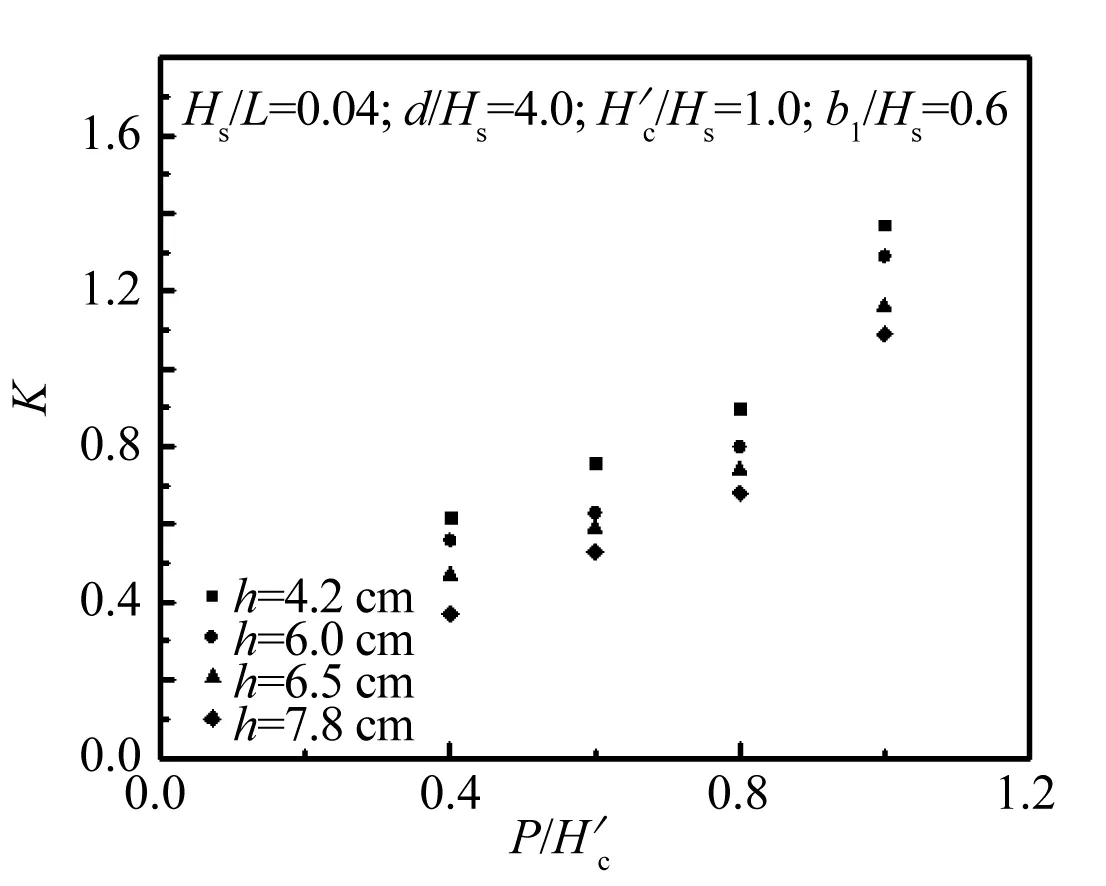
图16 K与的关系

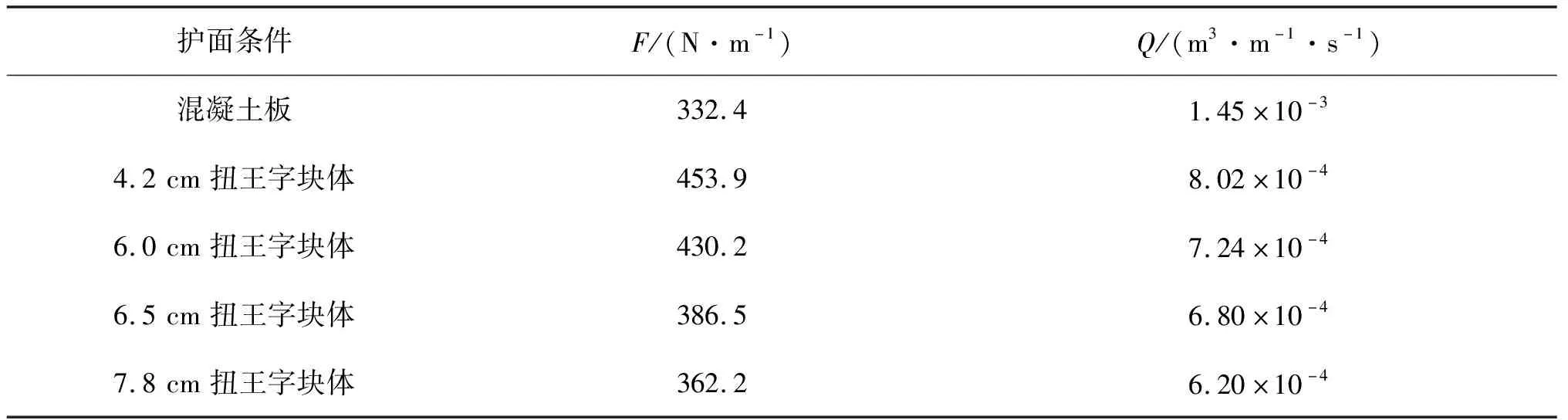
护面条件F/(N·m-1)Q/(m3·m-1·s-1)混凝土板332.41.45×10-34.2cm扭王字块体453.98.02×10-46.0cm扭王字块体430.27.24×10-46.5cm扭王字块体386.56.80×10-47.8cm扭王字块体362.26.20×10-4

3.6 单一变量分析h/Hs

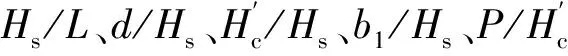
对于扭王字块体，由护面结构影响的折减系数在现行《防波堤设计与施工规范》[6]中推荐取0.6～0.7范围内的值。经过以上分析结果发现，斜坡堤在扭王字块体掩护条件下由护面结构影响的折减系数K并不局限于0.6～0.7的区间内，折减系数K的取值随波陡、相对水深、相对堤顶超高、相对坡肩宽度、相对胸墙高度和相对块体尺寸的改变都有较明显的变化。这是本文通过物模试验，对扭王字块体护面斜坡堤的新认知。

3.7 扭王字块体护面斜坡堤胸墙水平波浪力折减系数无因次计算表达式

(5)

上式相关系数R>0.90，满足非线性拟合的要求。物模试验值与式(5)的计算值对比如图18所示。如图所示，所有点在直线y=x两侧均匀分布，表明式(5)的计算值与物模试验值有较高的匹配度。

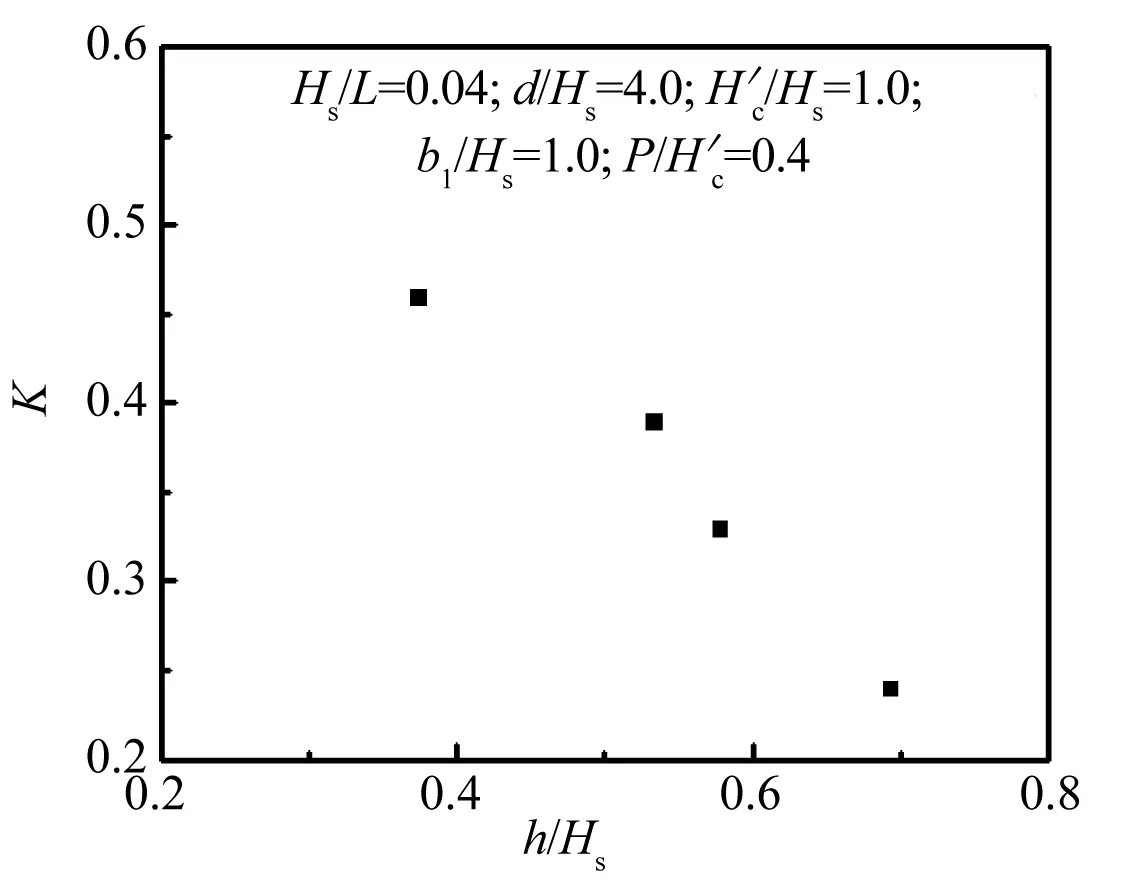
图17 K与h/Hs的关系

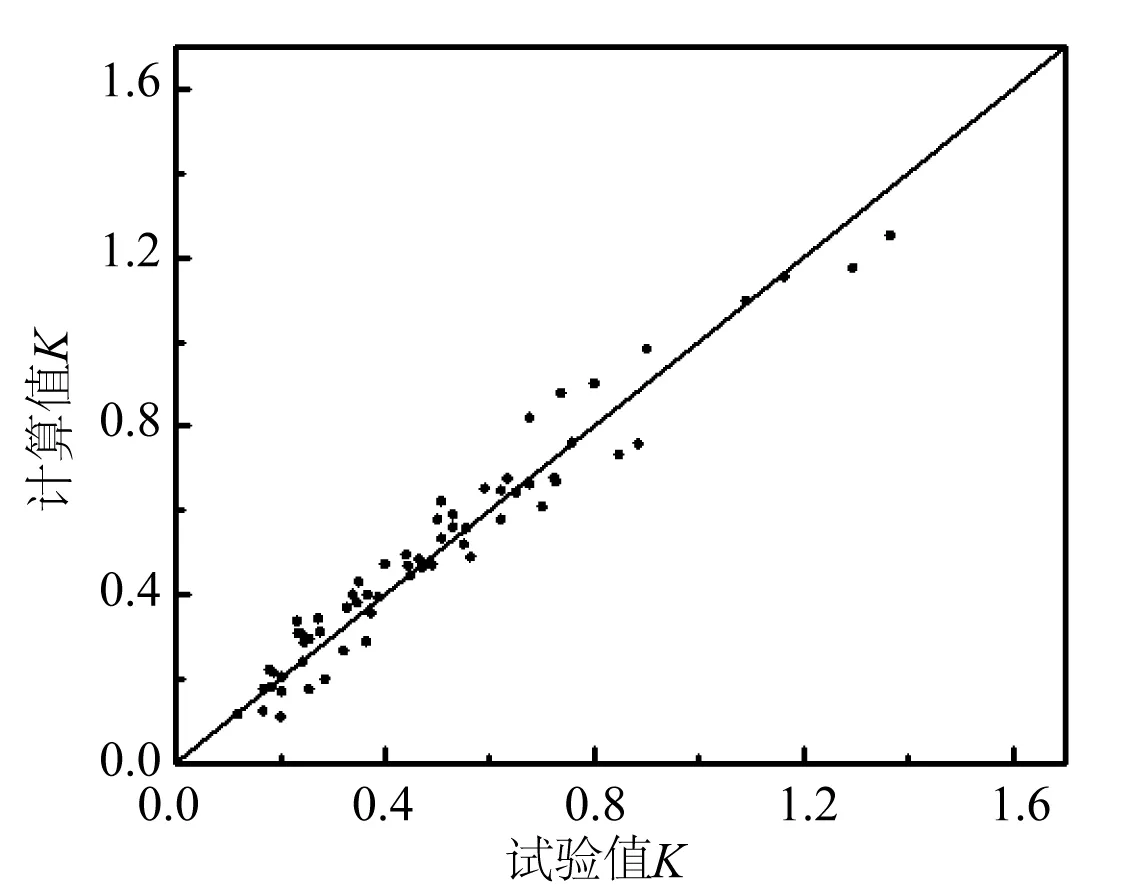
图18 K计算值与试验值对比

4 扭王字块体护面斜坡堤胸墙水平波浪力无因次计算表达式

通过以上单因素分析结果及公式拟合结果，对于坡度m=1.5的混凝土板护面斜坡堤，物模值与式(2)的胸墙水平波浪力计算值有较高的匹配度。因此，沿用规范编制思路，后文斜坡堤在混凝土板护面条件下胸墙水平波浪力均采用式(2)计算，进而得到坡度m=1.5扭王字块体护面斜坡堤胸墙水平波浪力无因次计算表达式：

(6)

式中：F表示斜坡堤在扭王字块体护面条件下的单宽胸墙水平波浪力，N/m；胸墙水平波浪力折减系数K采用式(5)计算。

为验证式(6)的精确性，对物模试验值和式(6)的计算值进行对比分析，分析结果见图19。如图所示，所有点在直线y=x两侧均匀分布，物模试验值与计算值有较高的匹配度，表明式(6)的计算精度较好。

为验证式(6)的适用性，选用杨洪旗等[10]物理模型试验工况(m=1.5)，应用式(6)计算相应工况下的斜坡堤在扭王字块体护面条件下胸墙水平波浪力值，与杨洪旗等[10]物理模型试验值进行对比，比对结果如表3所示。

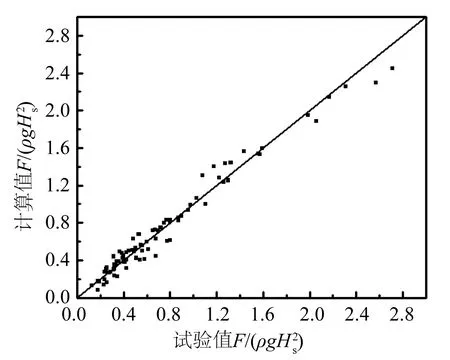
图计算值与试验值对比

表3 公式计算值与杨洪旗[10]胸墙水平波浪力物模值的对比(坡度m=1.5)

杨洪旗等[10]物模试验的斜坡堤断面堤脚有护底结构(和文中的试验断面图2略有不同)，试验内容为表3所示的case1～case16工况。对于胸墙水平波浪力，由表3的对比结果可以看出，在波陡、相对堤顶超高等六种因素的影响下，式(6)的计算值与杨洪旗等[10]物模试验值有较高的匹配度。且随着相对坡肩宽度的增加，式(6)计算值减小，与杨洪旗等[10]物模值具有一致的规律性；鉴于杨洪旗等[10]未做混凝土板护面斜坡堤胸墙水平力试验，表3中杨洪旗等[10]参考值K*采用杨洪旗等[10]物模试验值与本文混凝土板护面斜坡堤胸墙水平力计算值F板的比值，而采用式(5)的折减系数计算值与杨洪旗等[10]参考值K*吻合良好，且均不局限于《防波堤设计与施工规范》[6]中推荐的0.6～0.7取值范围。

5 结 语

1)现行《港口与航道水文规范》[5]中未就扭王字块体护面斜坡堤胸墙水平波浪力的计算方法做出具体规定。综合考虑波陡、相对水深、相对堤顶超高、相对坡肩宽度、相对胸墙高度和相对块体尺寸等因素，采用物模试验和多元回归分析方法，得出不规则波作用下混凝土板护面斜坡堤(m=1.5)胸墙水平波浪力的计算公式和胸墙水平波浪力折减系数的计算公式，进而给出了扭王字块体护面斜坡堤(m=1.5)胸墙水平波浪力的计算公式。通过与物模试验值、杨洪旗等[10]物模试验值的对比，证明文中提出的计算公式具有较好的精确性与适用性，研究成果丰富了规范内容。

2)对于扭王字块体护面斜坡堤，由护面结构影响的胸墙水平波浪力折减系数在现行《防波堤设计与施工规范》[6]中推荐取值范围为0.6～0.7。通过物模试验发现，对于扭王字块体护面斜坡堤，折减系数K值并不局限于0.6～0.7的区间内，折减系数K的取值随波陡、相对水深、相对堤顶超高、相对坡肩宽度、相对胸墙高度和相对块体尺寸的改变都有较明显的变化，为斜坡堤工程设计中胸墙水平波浪力折减系数的合理取值提供了参考依据。