近距离靠泊条件下钻井支持平台与生产平台相对运动研究

黄从亮，董 晴，吕海宁，王 晋

(1.上海交通大学 海洋工程国家重点实验室，上海 200240; 2.高新船舶与深海开发装备协同创新中心，上海 200240)

半潜式钻井支持平台主要用于海洋油气资源开发的相关海上支持作业，不但能够为生产平台提供钻井所需能源、钻井设备，储存生活物资等，还能够为海上作业人员提供舒适的生活环境，保证良好的人员休整效果。在近距离靠泊作业场景中，支持平台与生产平台构成了复杂的多浮体系统，浮体间的非线性波浪绕、辐射现象以及载荷的遮蔽效应等对平台运动产生复杂影响。多浮体系统的耦合水动力性能分析及运动响应预报一直是国内外学者研究热点。

多浮体耦合水动力分析方法主要包括理论分析、数值模拟和模型试验。早期学者们以单体水动力理论为基础，发展得到了多浮体三维势流理论，通过求解考虑浮体间波浪绕射、辐射的波浪速度势，得到相应波浪力，并通过运动方程分析浮体运动和受力响应。周文俊[1]在三维时域势流理论范畴内，利用混合格林函数法对两相邻Wigley型船和方形浮体的耦合水动力系数和波浪力作了计算分析，比较了多浮体系统与单浮体时延函数的不同。

随着计算机的发展，出现了大量以三维势流理论为基础的数值研究，主要为频域水动力参数计算和时域耦合分析。对于TLP生产平台-支持平台耦合系统，王月[2]通过频、时域计算，发现平台运动和系泊动力响应对浪向角比较敏感，工程运用中应将TLP作为迎浪平台；Dong等[3]详细研究了该耦合系统的相对运动响应，发现浮体之间同相位或反相位运动对相对运动和平台间栈桥运动响应影响显著，并基于瑞利分布给出了极限作业海况。对于波浪慢漂载荷的求解，单浮体可通过Newman近似或全QTF(full quadratic transfer function)矩阵计算得到。郭飞[4]讨论了波浪作用下两船并靠系统的模型模态、浪向、波浪频率和浮体间距对流场压力分布和二阶波浪力的影响，通过对比全QTF和Newman近似方法的二阶慢漂力计算结果，证实了Newman近似方法同样适用于多浮体系统。另外值得注意的是，由于势流理论忽略了水体黏性，多浮体系统在浮体间的狭窄水域内会出现水体共振[5-6]。为了抑制这种失真的水体过度升高现象，目前常采用加盖阻尼法对势流理论进行修正[7]。Xu等[8]将该方法应用于小间距驳船旁靠系统，证实了加盖阻尼法可以有效抑制过大的波面升高。除此之外，Shivaji等[9]通过计算流体动力学(CFD)直接考虑水体黏性的影响，在数值波浪水池内计算了两船旁靠系统的绝对和相对运动，详细说明了由于非线性入射波引起的非线性问题的重要性。

除数值计算之外，模型试验也作为多浮体响应研究可靠方法之一。Hong等[10]试验研究了浮式生产储油平台(FPSO)和液化天然气(LNG)运输船耦合系统在旁靠和串靠两种不同布置形式下的船体运动响应和相互作用力，发现串靠时波浪的遮蔽作用对低频运动影响显著，对波频运动影响不明显，且浮体间距的影响较小；旁靠时船体间相互干扰对低频和波频响应均有剧烈影响。徐乔威等[11]研究了风浪流联合作用下浮式液化天然气(FLNG)旁靠系统的运动和受力响应，发现斜浪下系统响应更明显。

基于上述研究，以具有实际工程背景的TLP生产平台与半潜式钻井支持平台多浮体系统为对象，通过数值模拟和模型试验研究近距离靠泊条件下的相对运动响应，为平台间连接栈桥的设计提供参考；在时域内分析对比考虑及忽略水动力干扰的两平台相对运动，探究水动力干扰在近距离靠泊条件下的不可忽略性；在此基础上，进一步计算不同海况下平台响应，探究波高对运动的影响规律。

1 多浮体水动力计算理论

假定流体无黏、不可压缩、流动有势，浮体做小幅简谐振荡运动，流体非定常速度势表示为：

(1)

Airy波的入射势为：

(2)

式中：ω、A、H为波浪圆频率、波幅和水深；g为重力加速度；k为波数，满足色散关系ω2=gktanhkH；β是入射波方向与x轴间的夹角，首浪为180°。

对于一个双浮体系统，辐射势φj满足：

控制方程(流域内)：

▽2φj=0

(3)

自由面条件：

(4)

水底条件：

(5)

物面条件：

(6)

远方辐射条件：

(7)

其中，(n1,n2,n3)=n,(n4,n5,n6)=(x,y,z)×n，n表示单位法向量且指向物面。

φ7与φj类似，只在物面条件上存在差异。φ7在两浮体的湿表面上满足：

(8)

上述速度势的边值问题可利用Green公式[12]转化为物面积分方程求解，进而利用伯努利方程计算出各浮体表面的动压力分布，并沿湿表面积分求得相应一阶流体力，包括波浪力和辐射力，同时求得浮体附加质量Aij和势流阻尼系数Bij：

(9)

(10)

其中，i,j=1, 2, ……, 12。当i,j=1, 2, ……, 6或7, 8, ……, 12时分别表示浮体1或2的水动力参数，其余项表示水动力相互干扰作用。

采用基于压力积分的近场法计算二阶波浪力F(2)，即流场速度势、压力场摄动展开后在物体瞬时湿表面(静水平均湿表面S0+波浪和运动引起的湿表面变化ΔS)上进行积分：

(11)

基于上述水动力参数和波浪力传递函数，双浮体系统的频域运动方程可表示为：

(12)

其中，Mij、Cij为浮体质量和静水回复力矩阵，Fi(ω)为波浪力。时域耦合运动方程可表示为：

(13)

其中，A(∞)为低频附加质量；R(t-τ)为迟滞函数，捕捉流体在特定时间动量变化对随后时间的影响，取决于浮体几何形状，可通过附加质量和势流阻尼来表达；F(t)为浮体所受外力，包括一阶、二阶波浪力，缆绳力Fm，风载荷Fw和流载荷Fc等。采用集中质量模型计算Fm，缆绳由无质量弹簧连接在一起的一系列质量块模拟，通过求解悬链线方程得到缆绳对船体的作用力。采用OCIMF方法(式(14))计算风、流载荷,F为纵荡、横荡或艏摇力、力矩，ρ为空气或海水密度，V为流体流过浮体的相对速度，A为面积。

F=0.5ρV2A

(14)

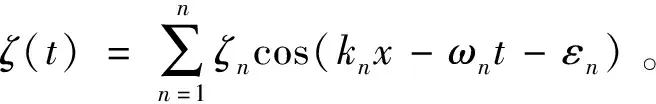
(15)

相似地，二阶时域波浪力(忽略二阶和频波浪力)为：

(16)

其中，QTF-(ωm,ωn)为二阶差频波浪力传递函数，在二阶平均波浪力的基础上采用Newman近似方法[13]计算得到：

(17)

将上述时域水动力参数及外力代入时域运动方程，采用隐式积分方法求解，时间步长为0.5 s，可求得不规则波作用下的浮体响应。

2 研究对象

2.1 坐标系定义

如图1所示定义耦合系统总体坐标系O-XYZ及两平台局部坐标系o1-x1y1z1和o2-x2y2z2。

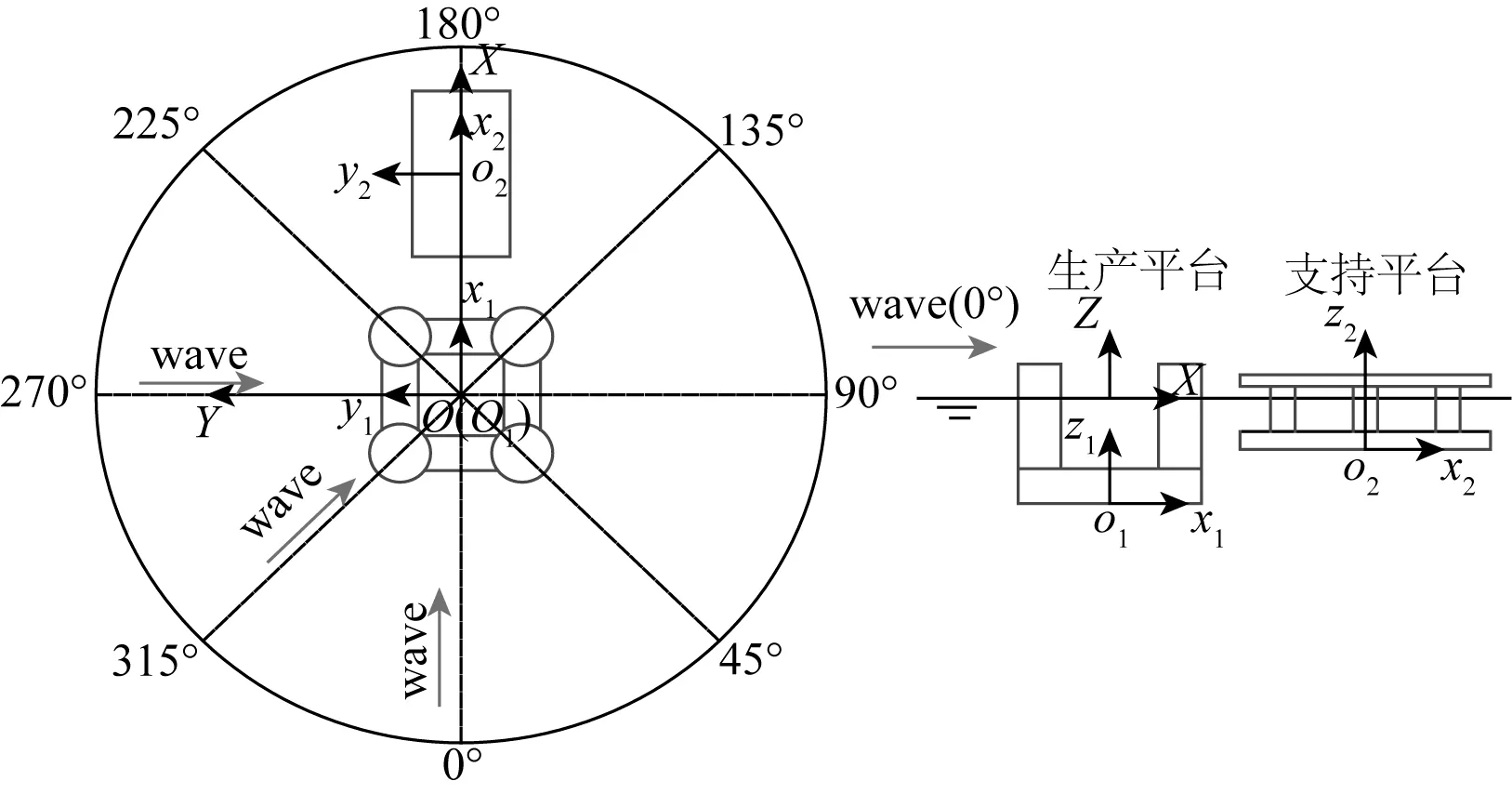
图1 坐标系定义

2.2 模型参数及数值计算

TLP生产平台由平台主体、张力腿和立管系统组成，钻井支持平台主要由6个方形立柱、2个浮筒和3个横撑组成，二者主要参数分别如表1、2所示。

表1 TLP生产平台主体参数

表2 钻井支持平台主要参数

耦合系统共采用10根系泊缆定位，每条均由钢丝绳-锚链-钢丝绳-锚链组成；平台间采用4根带缆连接以限制相对运动，均为锚链-尼龙绳-锚链三段式。系泊缆及带缆如图2所示布置。

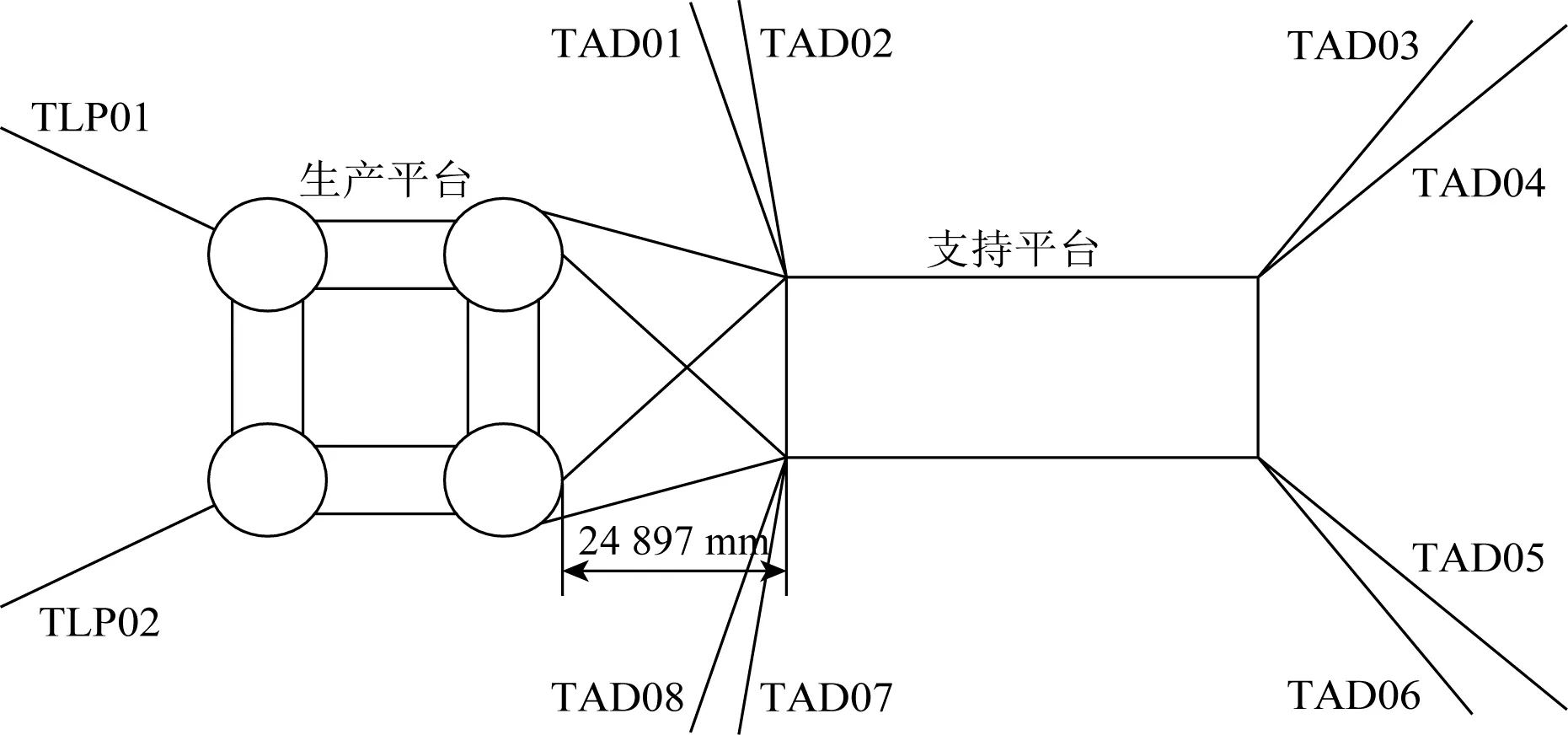
图2 两平台系泊系统布置

采用HydroD软件计算频域水动力参数，包括运动响应及波浪力传递函数等；使用Orcaflex软件在时域内对整个系统进行模拟，包括两浮体、TLP平台张力腿和立管系统、平台间连接带缆及系泊定位系统，充分考虑各成分间的非线性耦合效应。时域数值模型和计算波浪条件分别如图3和表3所示。

图3 时域数值计算模型

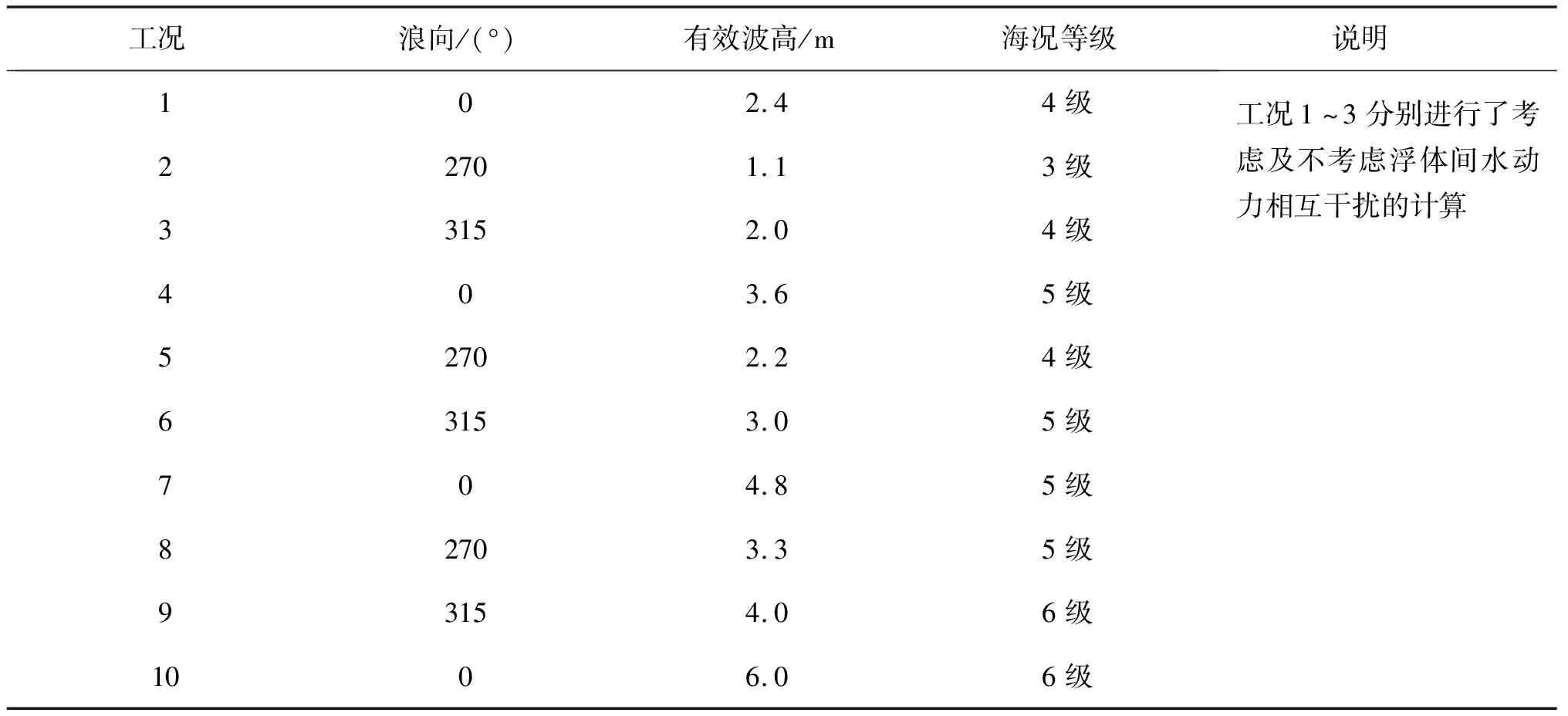
表3 时域计算波浪条件

3 模型试验

图4 模型试验

为了验证数值方法的可靠性，在深水试验池中进行模型试验(图4)，试验选取三个典型工况，如表4所示，考察不同海洋环境条件下两平台的相对运动。不规则波浪采用JONSWAP波浪谱，风浪流方向一致。

根据单平台衰减试验结果，TLP平台纵荡、横荡、垂荡固有周期分别为94.9 s、98.3 s、2.87 s，横摇、纵摇、艏摇固有周期分别为2.41 s、2.35 s、64.9 s；钻井支持平台垂荡、横摇、纵摇固有周期分别为16.9 s、35.8 s、20.4 s。试验结果符合常规TLP和半潜平台的周期范围。

表4 模型试验工况

4 结果与分析

4.1 单浮体运动响应幅值算子(RAO)

图5为单一钻井支持平台与TLP平台分别在0°和315°环境条件下纵荡、垂荡、纵摇数值模拟和白噪声波浪试验结果比较，结果表明单浮体数值计算结果与试验基本吻合较好，数值模型可靠。TLP 平台在垂荡、纵摇RAO上存在明显差异，这是由于平台运动幅值很小(垂荡<0.015 m/m，纵摇<0.03°/m)，受光学运动采集系统精度限制，导致数值与试验结果相差较大。

图5 单一平台运动响应数值计算与试验结果对比

4.2 相对运动响应

对两平台耦合系统在考虑浮体间水动力相互干扰的情况下开展时域计算，计算工况见表4，模拟时长3 h。假定两平台之间沿X轴设有一个可伸缩栈桥，将平台运动响应结果通过坐标转换至平台间连接栈桥处的相对运动。图6为响应时历与对应频率谱结果对比，相应栈桥端点处相对运动统计值列于表5。

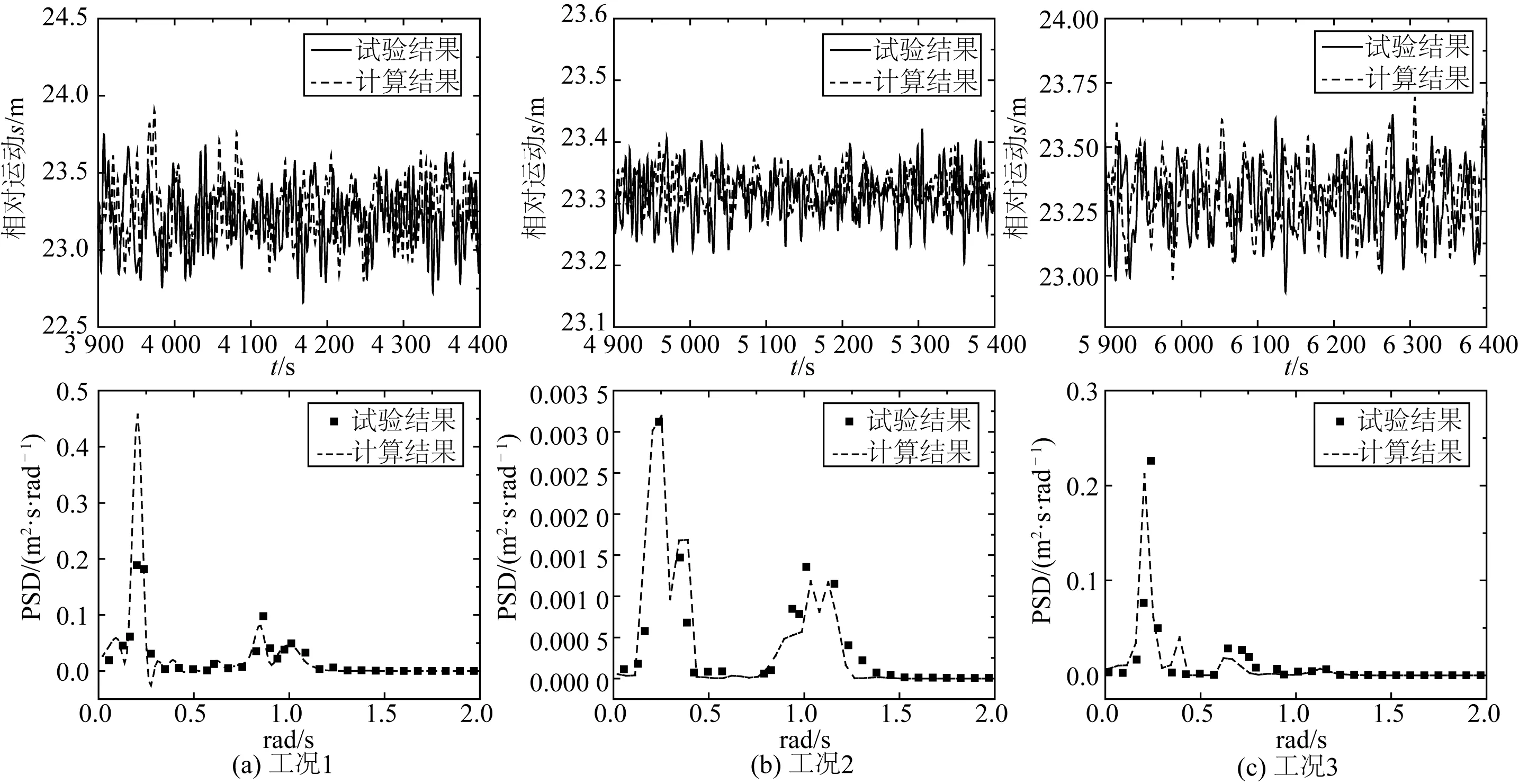
图6 栈桥处相对运动响应时历与频率谱(考虑浮体间水动力相互干扰)

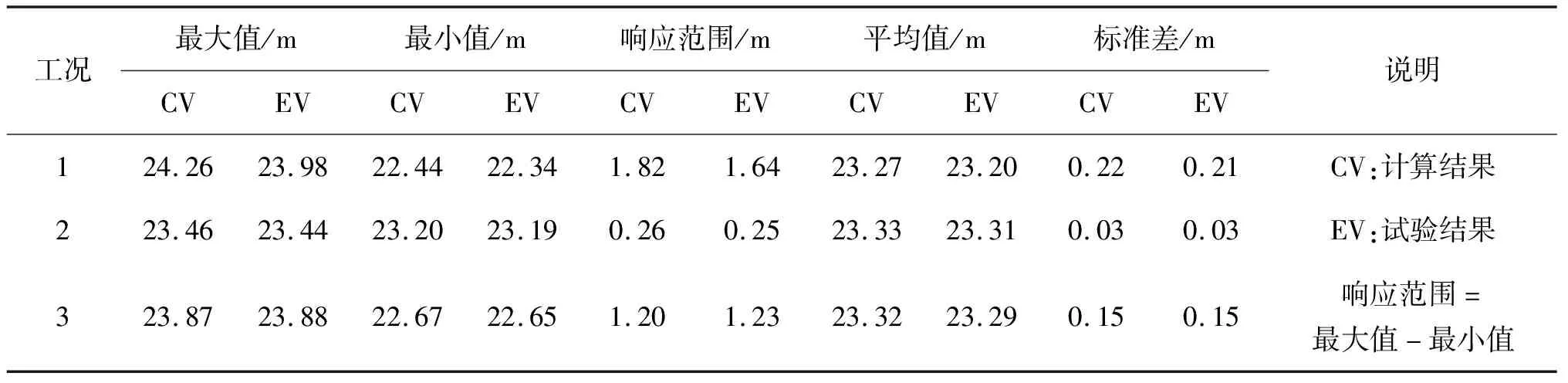
表5 栈桥处相对运动统计值(考虑浮体间水动力相互干扰)

图6、表5表明数值计算结果与试验结果基本一致，说明采用上文频、时域结合，Newman近似方法计算二阶波浪慢漂力且考虑浮体间水动力相互干扰的计算方法可靠，能够正确反映多浮体耦合系统中平台的运动响应特性。

栈桥处最大相对运动幅值出现在工况1中，其响应幅值接近2 m，此时环境入射方向为0°，即两平台沿来浪方向串靠布置且TLP生产平台迎浪。由于栈桥的布置方向与环境入射方向平行，因而此时较大的平台间相对纵荡运动会对栈桥运动响应产生显著影响，在栈桥设计时应留有足够的安全系数。最小相对运动幅值出现在工况2中，此时环境入射方向为270°，即两平台垂直于来浪方向旁靠布置，此时平台间相对纵荡运动较小，使栈桥相对运动较小。在实际工程应用中，为保证栈桥安全作业，采用工况2布置形式更为有利。

4.3 水动力相互干扰的影响

为了明确浮体间水动力相互干扰对平台运动响应的影响，以下在不考虑耦合水动力的情况下计算平台相对运动响应。计算方法同上文类似，仅忽略频域水动力参数中的两浮体相互干扰项，即附加质量Aij和势流阻尼系数Bij矩阵中i=1, 2, ……, 6且j=7, 8, ……, 12和i=7, 8, ……, 12且j=1, 2, ……, 6项。表6给出了忽略水动力干扰时栈桥处相对运动统计结果。

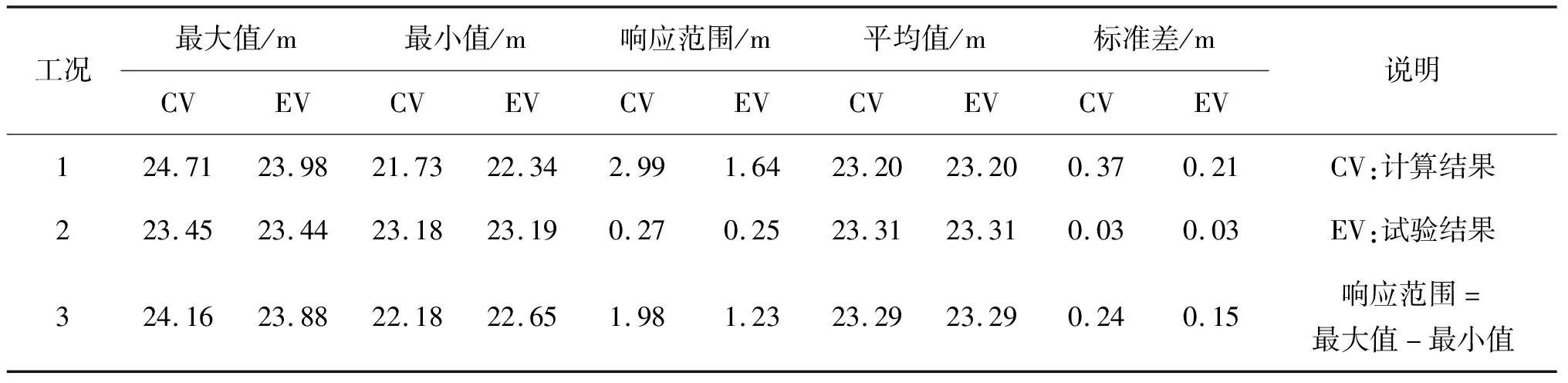
表6 栈桥处相对运动统计值(忽略浮体间水动力相互干扰)

比较可知，除工况2即横浪方向相对运动幅值模拟较为准确之外，另外两个工况计算值明显远高于试验值。对于工况2，环境载荷方向为270°，即两平台旁靠布置且垂直于来浪方向，平台间水动力相互干扰较小，即使忽略干扰对计算结果亦不会产生较大影响。对于浮体相互干扰明显的工况1，此时两平台沿来浪方向串靠布置且TLP平台迎浪，前方迎浪平台的存在会显著干扰后方背浪平台的环境载荷，即波浪经过迎浪平台后会发生复杂的绕、辐射现象，部分波浪能量衰减，对背浪平台遭受的波浪载荷起到遮蔽作用，导致浮体运动响应相比于忽略水动力干扰时较小；忽略耦合水动力时，相对运动的数值预报结果接近于试验值2倍，表明该简化方法存在较大误差。通过比较上述两种情况，可得出结论：平台近距离靠泊时，横浪作用下基本可忽略浮体间的水动力干扰，其他浪向下耦合水动力对响应影响明显，不可忽略。

4.4 不同海况对相对运动的影响

在考虑水动力相互干扰的情况下进一步探究不同海况条件对平台运动响应的影响规律，相应工况(见表4)下栈桥处相对运动响应幅值如图7所示。

图7 不同海况条件下栈桥处相对运动幅值

计算结果表明，在海况小范围变化内，平台间栈桥相对运动响应幅值与波高之间基本呈线性关系，因为多浮体水动力分析过程中采用线性势流理论计算浮体运动响应。此外，当海况达到一定强度时，需要考虑两平台先达到碰撞条件还是连接带缆断裂的条件。为了探讨该问题，计算了较高海况下(有效波高为6 m)，TLP生产平台迎浪时的系统响应。表7给出栈桥运动响应和非交叉带缆张力的统计值，其中栈桥运动最小值仍远大于0，且带缆有效张力为正，说明两平台仍未发生碰撞，但此时带缆有效张力最大值为4 655.30 kN(474.7 t>450 t)，已经超过带缆的破断强度，表明连接带缆已发生断裂。因此在0°浪向条件下，应优先考虑环境恶化时带缆是否失效。

表7 栈桥运动响应和非交叉带缆张力统计值

5 结 语

采用数值计算与模型试验相结合的方法，对TLP生产平台与半潜式钻井支持平台多浮体耦合系统的平台、栈桥相对运动响应做了研究，探讨了多浮体水动力相互干扰作用对平台运动响应的影响，在此基础上通过数值计算研究了输入波高与运动响应幅值的关系，得出以下结论：

1)通过数值计算与试验结果对比，发现在考虑水动力相互干扰情况下，数值模拟结果较为准确。

2)通过比较考虑和忽略浮体间水动力相互干扰时的运动响应结果，可知TLP生产平台和半潜式钻井支持平台在近距离靠泊时，除在横浪作用下，即两平台旁靠布置且垂直于来浪方向，其他情况下不可忽略耦合水动力的影响，而横浪条件下由于平台对载荷遮蔽效应较小，浮体间水动力相互干扰不明显。

3)通过对不同海况下平台响应进行探究，发现在海况小范围内变化时，运动幅值与波高之间基本呈线性关系。

4)当海况达到六级，有效波高达6 m时，TLP顶浪状态下平台间的带缆张力已超过其破断强度，而此时两平台未发生碰撞，说明随着海况的恶化，两型平台在碰撞之前连接带缆已经断裂，在设计时应合理选择连接带缆的参数。