内孤立波作用下柔性跨接管动力性能研究

李效民，孙宏伟，王乐瑶，李 朋

(1.中国海洋大学 工程学院，山东 青岛 266100; 2.青岛大学 数据科学与软件工程学院，山东 青岛 266071; 3.山东科技大学 土木工程与建筑学院，山东 青岛 266590)

活跃在中国南海的内孤立波已经成为该地区海洋油气资源开发所不得不考虑的环境荷载[1-3]。1990年，内孤立波通过流花油田平台时，导致系泊缆绳破裂、船只相互碰撞、漂浮软管被挤破[4]，内孤立波对南海海洋工程结构的安全构成了重大风险，因此在海洋工程结构的研究和安全评估中应该考虑内孤立波的影响。

跨接管是连接水下油气储存开采设施与海面油气处理设施的重要装置。通常情况下跨接管并不是搁置在海床上，而是悬挂在上述两点之间，处于自由悬链线状态。跨接管整体位形距离海面较近，通常不设置限弯器。柔性跨接管由于没有侧向支撑，易受到海流、波浪的影响。同时由于海面设施与水下设施间常常发生相对运动，跨接管的运动状态将变得十分复杂。柔性跨接管作为管道运输中重要的一环，众多学者对跨接管设计、安装及使用等方面展开了深入研究。Blevins等[5]首先提出了高顺应性跨接管的设计步骤，对两端点高度接近水平的跨接管进行了模态与内力分析等，给出了跨接管的设计步骤。Sele等[6]研究了钛金属跨接管的性能，结果表明钛金属跨接的适用范围更广，可将其应用在高温高压的深水环境中，从材料的角度对跨接管进行了分析。Huang[7]采用计算流体力学(CFD)法对跨接管的涡激振动进行了研究，结果表明跨接管的涡激振动较为复杂，呈现出一定程度的随机性，必须重视跨接管的抗疲劳设计。Huang等[8]和Zhen等[9]对张力系泊式水中生产(STLP)系统中的跨接管进行了静态分析、模态分析和动态分析，研究了基于STLP系统概念的柔性跨接管的关键全局设计准则和分析过程，进一步阐明了特殊体系内跨接管设计中的重难点。随着跨接管设计要求的不断提高，许多新方法被不断应用到跨接管的设计中。Low和Langley[10]采用集中质量法对频域和时域内的柔性跨接管进行了动态分析。可以看出，众多学者围绕跨接管的设计步骤、材料属性、静动力分析、疲劳分析、优化设计等方面开展了广泛而卓越的研究，已经能够较好的满足跨接管的设计要求。但关于内孤立波对跨接管的影响并未引起足够的关注，当前缺少这方面的深入研究。当采用双层流模型对内孤立波进行简化时，模型中的上层流速较大，作用时间长，由于跨接管的工作水深较浅且常常与内孤立波上层部分重合较多，又没有侧向支撑，因此在中国南海等内孤立波频发海域跨接管的设计当中必须考虑内孤立波带来的影响。

文中基于KdV理论和向量式有限元理论[11-12]，对内孤立波作用下的跨接管进行了三维空间下的动力响应特性分析。首先采用KdV理论对内孤立波场中水质点速度和加速度进行分析；接着基于向量式有限元理论建立了跨接管的动力分析和计算模型；最后通过算例对内孤立波作用下的跨接管进行静动力分析，研究其动力响应特性。总结得到的相关结论以期为跨接管的设计和安全运行提供借鉴和指导。

1 基于KdV理论的内孤立波水质点运动方程

内孤立波机理比较复杂，当前人们对于内孤立波的生成与传播机制尚不十分明确。当前研究大多假设海水是密度均匀稳定层化的两层流体，采用双层流模型对其进行模拟。建立如图1所示的双层流体和坐标系模型，上层流体密度为ρ1，流体厚度为h1；下层流体密度为ρ2，流体厚度为h2；总水深为h=h1+h2。坐标系中oxy平面位于两层分层的流体内界面(密度跃层)处，ox轴指向内孤立波的正传播方向，oy轴垂直于纸面，oz轴垂直向上为正。设定ζ表示内孤立波界面位移，η0表示振幅，Cp表示内孤立波传播速度。

图1 双层流模型

通常情况下跨接管所在的工作区域水深h较大。当0/h<0.1时，采用KdV方程[13-15]对内孤立波进行模拟比较准确。KdV方程的理论解界面位移表达式为：

ζ(x,t)=η0sech2Δ

(1)

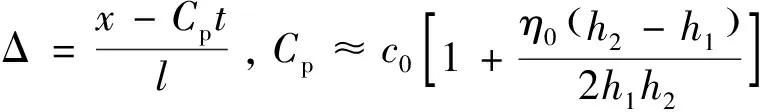
(2)

(3)

2 跨接管动力分析模型的建立与求解

2.1 基于向量式有限元的跨接管整体建模思路

将所研究对象看作是由无数多个点组成的一个物理连续体，在这无限多个点之中根据问题的要求选取一组点，以此描述研究对象的形状和位置，其他点的位置可用一组连续的标准化内插函数来表示。

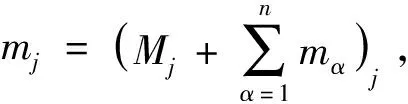
2.2 构件空间点的点值描述

当杆件受到外力作用发生运动时，任意一个空间点j的位置是与时间相关的函数。在一段时间内，用一组时间点上的点值来描述它的轨迹。如图2所示，假设空间点j在ta、t、tb位置向量分别为Xa、X、Xb，时段ta≤t≤tb就是一个途径单元。

图2 途径单元

2.3 主轴坐标及杆件元的变形

为了表示出三维空间弯曲杆件结构的内力。采取先求出梁截面的主轴方向，采用主轴坐标来描述，再转化为域坐标的方法。

(4)

(5)

所以在每一个途径单元的起始点，该起始点的主轴方向加上该时段内的转动向量可以得到下一时刻新的主轴方向。为消除刚体的平移与转动，将杆件进行虚拟的逆向运动。取节点 1作为参考点，设定u1为平移向量。如图4，经过逆向平移，得到元节点(1b,2b)相对参考点(节点(1a，2a))的相对位移向量。

η1=0，η2=u2-u1

(6)

刚体转动向量的大小可以用相应时刻点的主轴方向转动向量γb来表示。

利用逆向运动，消除刚体的平移与转动，得到ta时刻杆件存在的位移和转角便是导致内力产生的真实转角和变形位移。

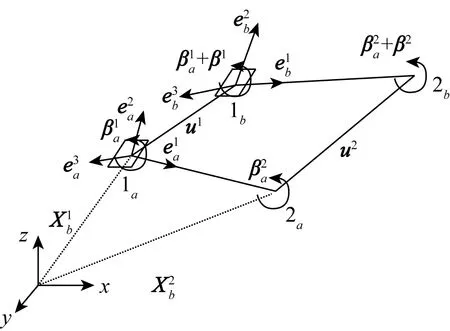
图3 主轴坐标及杆单元变形

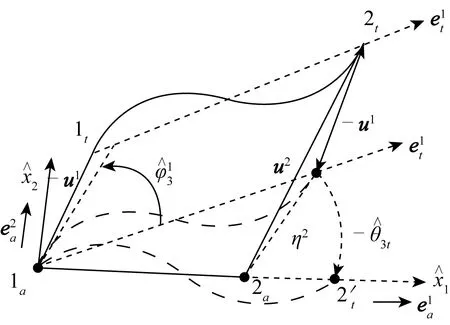
图4 虚拟的逆向运动

2.4 单元节点内力计算

2.5 水动力荷载

跨接管的水动力载荷可用Morison[16]修正方程进行计算。

(7)

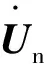
2.6 控制方程

质点j的控制方程在考虑结构阻尼的情况下可以写为：

(8)

(9)

2.7 控制方程式的求解

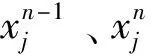
(10)

(11)

其中，C1=1/(1+ξh/2)，C2=C1/(1-ξh/2)。

3 内孤立波作用下跨接管的动力性能

3.1 算例验证

参照文献[10]选取跨接管的参数如表1所示，并采用集中质量法对该跨接软管的内力与位形进行了建模与分析。该跨接管两端点的垂直距离为50 m，水平距离为100 m，顶端固定在海平面以下5 m处。采用66个节点将跨接管分为65个杆单元，跨接管所在平面为x-z平面，左端点坐标为(0，0，-55)，为1号节点。假设跨接管的两端铰接，对于跨接管内部的流体仅考虑其质量。选取两种线性波浪工况与文献[10]进行对比分析，波高为10 m，周期为10 s，分别在0°和90°即平面内及平面外两个方向施加规则波，如图5所示。通过图5的对比分析，可以看出向量式有限元法得到的结果与集中质量法所得结果吻合较好，只在最大值与最小值上存在小于1%的差距，说明基于向量式有限元法的动力分析程序是可靠的。

表1 跨接软管参数

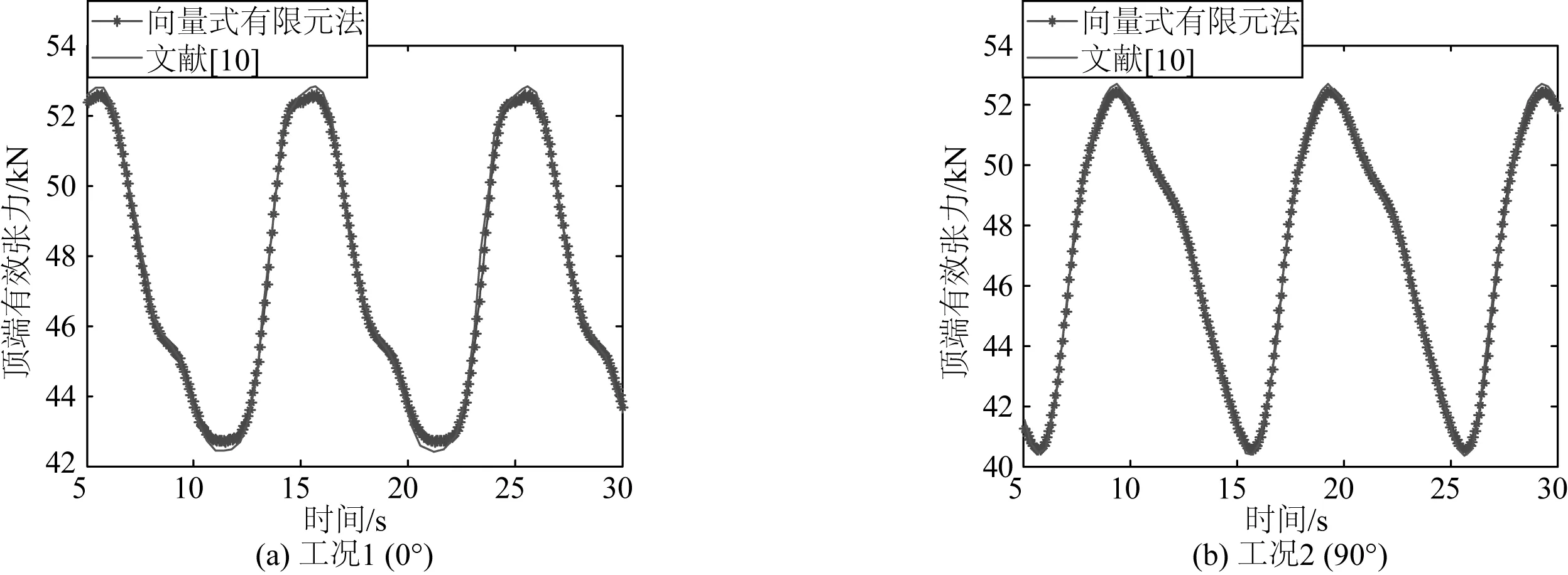
图5 两种工况下跨接管的顶端有效张力对比分析

3.2 内孤立波作用下的跨接管动力性能分析

根据Cai等[2]对南海内孤立波观测资料的总结分析，得到此内孤立波的基本特征参数。取上层水深h1=70 m，密度ρ1=1 025 kg/m3，下层水深h2=844.4 m，密度ρ2=1 028 kg/m3，内孤立波的振幅为η0=-75 m。由于η0/h<0.1，所以符合KdV方程应用条件。据内孤立波的参数选用上文中提到的KdV理论进行模拟，得到波面函数ζ(X)，其中X=x-ct。固定横坐标为跨接管的位置坐标x=2 000 m，则波面函数为一个只有自变量t的函数ζ(t)。图6为初始时刻内孤立波的波面形状与跨接管的位形，角α为内孤立波来流方向在XOZ面内与X轴正方向的夹角。

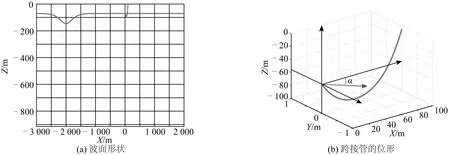
图6 内孤立波的波面形状与跨接管的位形

采用莫里森方程对内孤立波所引起的作用力进行计算，α取0°，得到内孤立波经过时对跨接管的作用力f(x,y,z,t)，将其带入跨接管的控制方程中，计算跨接管的动力响应。保持其他条件不变，仅改变内孤立波的入射角α为45°、90°、135°、180°。图7分别为初始位形，以及内孤立波入射角为0°、45°、90°、135°、180°时跨接管发生最大位移时的空间及各平面视角下位形图。

图7 不同角度下跨接管发生最大位移时的位形与原始位形

图8和9分别为不同角度的内孤立波作用下跨接管的张力包络图和弯矩包络图，纵轴为沿管长方向。

图8 张力包络图

图9 弯矩包络图

从图7中可以看出在内孤立波的作用下跨接管会产生较大的偏移，在内孤立波作用频繁的区域可能会导致跨接管的疲劳效应加剧，在某些特殊角度下内孤立波会导致跨接管的整体抬升。并且从图7跨接管的位形可以看出90°时跨接管的位移明显大于其他入射角度，主要原因是当内孤立波夹角为90°时，跨接管的受力面积大而跨接管侧向刚度低。从图8和图9中可以看出，当内孤立波的入射角为180°时跨接管的张力和弯矩最大，这是因为当内孤立波的入射角度变为180°时，此侧跨接管受力较大加剧了其平面内弯曲的趋势。

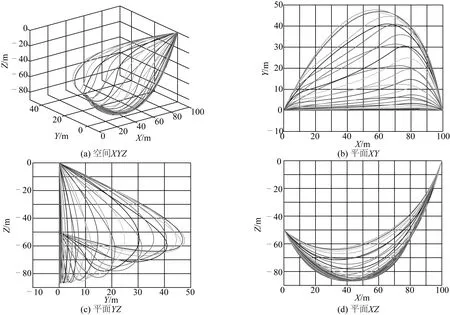
图10 入射角为90°时的跨接管位移包络图

从图11中可以看出当内孤立波的入射角变为90°时，内孤立波整体的运动趋势与流速变化趋势相同，最大位移发生在内孤立波波峰经过跨接管时，最大位移为53.2 m。在应对内孤立波可能造成的灾害时，应尤其注意内孤立波波峰经过跨接管时所造成的影响。

顶端张力与底端张力的大小是跨接管在位安全稳定运行的重要条件，有必要对不同入射角度下的跨接管的顶端与底端张力进行研究。图12和图13分别为内孤立波入射角度不同时跨接管的顶端和底端张力时程曲线。顶端张力与底端张力的具体数值可以参照表2。从图12和图13及表2中可以看出，张力的变化趋势与流速息息相关，不同入射角度下的跨接管的张力变化区间不同，张力峰值都出现在波峰经过跨接管时。但随着入射角度的改变，跨接管的张力变化形式也随之改变。当入射角度为0°、45°和90°时跨接管的顶端张力与底端张力先增加后减少，而当入射角度为135°和180°时跨接管的顶端张力与底端张力先减少后增加。

图11 不同深度处跨接管的位移时程曲线

图12 顶端张力时程曲线

图13 底端张力时程曲线

表2 不同入射角度下的顶端与低端张力

3.3 不同振幅内孤立波作用下的跨接管动力性能分析

振幅是内孤立波的重要变量，探究不同振幅的内孤立波对跨接管的影响程度十分必要。从前文计算中可以发现入射角度为90°的内孤立波所带来的影响最大。由于变量较多，仅取内孤立波入射角为90°的情况进行验算。表3中列出了不同振幅作用下立管的顶端张力与底端张力的最大值与最小值。图14为不同振幅的内孤立波作用下的跨接管，发生最大位移时的空间及各平面视角下位形。

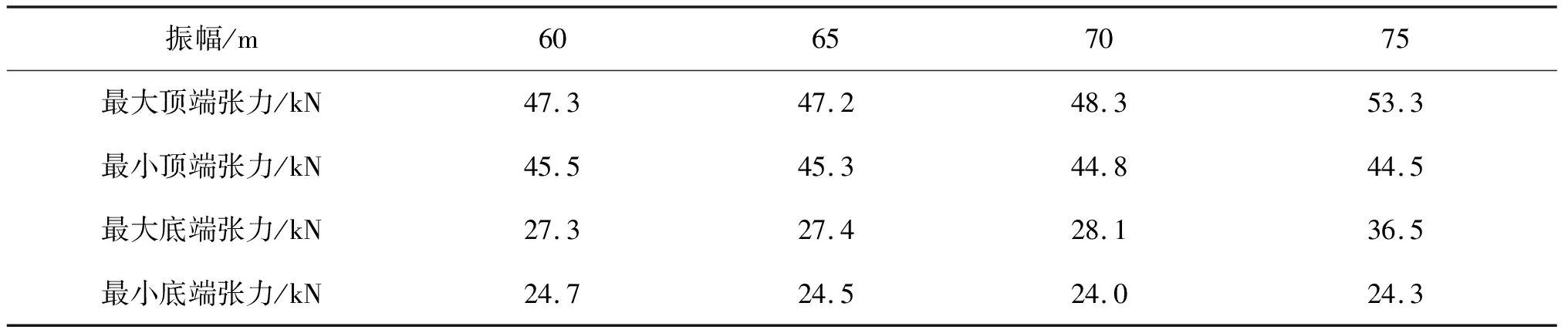
表3 不同振幅作用下的顶端与底端张力

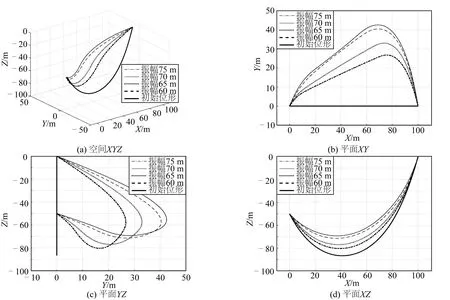
图14 不同振幅下跨接管发生最大位移时的位形图与原始位形

从表3中可以看出内孤立波振幅的增大，会导致跨接管的底端张力与顶端张力的极值发生变化，变化幅值增大。从图14中可以看出，内孤立波振幅的增长会导致跨接管的最大位移增大。跨接管的位形也会因为内孤立波振幅的不同而不同。在内孤立波荷载的验算当中，应当注意内孤立波振幅变化给跨接管带来的影响。

4 结 语

以跨接管为研究对象，基于向量式有限元法建立了跨接管的动力计算和求解模型，分析了其在内孤立波作用下的动力响应特性。通过研究得到结论如下：

1)在内孤立波作用下，跨接管会产生较大的空间位移，也会导致跨接管的整体抬升。如文中管长仅170 m的跨接管会产生53.2 m的位移，跨接管远远偏离其初始位置。在不采取相关措施的情况下可能会与其他海洋设施发生碰撞，影响跨接管的安全在位稳定运行。

2)内孤立波作用下的跨接管存在一个明显的动力过程，会引起柔性跨接管的内力发生突然变化，整个变化的周期与内孤立波周期相同。在文中的算例中，当夹角为0°，45°，90°时，跨接管的顶端张力与底端张力会先增大再减小，135°和180°的内孤立波将会导致跨接管的顶端张力与底端张力先减小再增大。

3)柔性跨接管的动力响应与内力变化与内孤立波入射角度息息相关。柔性跨接管对于内孤立波的入射角十分敏感，在内孤立波频繁发生的区域，可以适当根据内孤立波来向优化跨接管的安装方位以减少内孤立波所带来的影响。

4)柔性跨接管对内孤立波振幅的变化较为敏感，在一定范围内的内孤立波振幅的增长会导致柔性跨接管的顶端底端张力极值增大，同时还会导致柔性跨接管的运动状态位置形状发生变化。在关于柔性跨接管的内孤立波荷载的计算当中，应当考虑内孤立波振幅不同可能会带来的影响。

通常情况下，当内孤立波经过海洋平台时，也会导致海洋平台的运动。当这两种运动同时发生时，可能会导致意想不到的结果发生。在柔性跨接管的设计使用中，必须注意内孤立波可能带来的影响。