面向密文图像信息隐藏的随机插值方法
孙容海, 施林甫, 俞春强, 劳 欢, 唐振军
广西师范大学广西多源信息挖掘与安全重点实验室,广西桂林541004
图像信息隐藏技术[1-5]主要通过修改载体图像中的不重要信息来隐藏秘密数据,在版权保护、隐蔽传输和内容鉴定等方面有重要应用.一般而言,修改操作不可避免地引起载体图像失真,然而军事、医学图像等应用场景不允许原始图像有失真,要求实现可逆地嵌入秘密信息,即提取完秘密信息后,原始载体图像能够被无损恢复.针对可逆方式的信息隐藏需求,研究人员开展了针对图像载体的可逆信息隐藏研究.通常,可逆图像信息隐藏可分为面向明文图像的可逆信息隐藏和面向密文图像的可逆信息隐藏.
面向明文图像的可逆信息隐藏,其主流的技术有无损压缩[6-7]、差值扩展[8-9]和直方图平移[10-13]等.无损压缩技术通过无损压缩图像的最低有效位(least significant bit, LSB)或量化残差获取隐藏空间,因为无损压缩率较低,所以这类方法隐藏容量小,大多应用于图像鉴定和水印等方面.差分扩展技术计算相邻一对像素的差值,将该差值扩展两倍,秘密信息隐藏在扩展后差值的LSB 位中,这类方法隐藏容量约为0.5 bpp(平均一个像素隐藏的比特数).直方图平移技术通过平移像素直方图或预测差值直方图嵌入秘密信息.由于基于直方图平移的方法具有较大的隐藏容量和较好的载密图像质量,因此近年研究人员更多关注直方图平移技术.
密文图像可逆信息隐藏算法将秘密信息嵌入到密文图像中生成载密图像,对载密图像解密和提取秘密信息后,能够无损恢复原始密文图像.这类算法包括不可分离可逆信息隐藏算法[14-16]和可分离可逆信息隐藏算法[17-24]两大类.不可分离算法的特点是接收端需要同时掌握加密密钥和隐藏密钥才能提取信息和解密图像,并且不能互换解密阶段和信息提取阶段的次序.如果互换次序,则信息无法准确提取,图像也无法准确恢复.可分离算法的特点是图像解密和信息提取是独立分离的,接收端可以根据密钥的掌握情况执行不同的操作.如果仅有加密密钥,只能对图像进行解密;如果仅有隐藏密钥,只能提取秘密信息;如果同时拥有两者,不仅能提取秘密信息,还能无损恢复原始图像.
下面简要回顾一些有代表性的密文图像可逆信息隐藏算法.例如,文献[14]首次提出密文可逆信息隐藏算法,是密文图像可逆信息隐藏研究的开创性工作.该算法采用高效的流加密方法对图像进行加密.隐藏时,对密文图像分块,通过取反图像块内一半像素的低3位,实现在每个图像块中嵌入1 比特数据.在接收端,通过波动函数提取秘密信息和恢复原始图像.当分块较小时,该算法的信息提取和图像恢复会出现错误.文献[15]通过改进文献[14]的波动函数并加入边信息来减少图像恢复和信息提取的错误率,提高了隐藏容量.文献[16]考虑块内不同像素的位置,设计一种分块复杂度计算方法,提高了信息提取的正确率.文献[17]提出一种可分离密文图像可逆信息隐藏算法,该算法通过压缩密文图像的LSB 获取稀疏空间,再将秘密信息嵌入到稀疏空间.为了进一步提高压缩比,从而提高隐藏容量,文献[18]利用低密度校验码对密文图像像素的低比特位进行压缩得到较大的隐藏空间.文献[19]利用非加密的可逆信息隐藏算法将部分信息自嵌入到其他部分以获取嵌入信息的空间,该算法具有较大的隐藏容量和低失真的特点.文献[20]从明文图像中选取目标像素,然后采用差分扩展方法将目标像素自嵌入到明文图像中,再采用Paillier 加密方法进行加密,生成密文图像.隐藏时,将秘密信息进行分组并转换成十进制数,由十进制数和偏移量构成伪装像素,通过替换目标像素实现隐藏.文献[21]先用密文图像像素的LSB 替换alpha 通道透明值的LSB,接着用比特替换方法在alpha 通道透明值的高7 位和密文图像像素的LSB 中隐藏信息,最后用密文图像和alpha 通道构造密文PNG 图像.文献[22]采用比特位异或的方法对图像进行加密,根据随机函数确定密文图像中的载体像素,采用高位取反的方法隐藏信息.提取信息时,先对图像解密,由于像素高位存在0 或1 两种可能且其中一个为原始比特位,因此采取曲面插值预测的方法计算这两种可能预测差值,通过对比两种预测差值大小提取秘密信息及恢复图像.文献[23]在加密前计算像素预测差值,由于预测差值直方图分布近似拉普拉斯分布,因此采用哈夫曼编码对预测差值进行无损压缩,得到较大的隐藏空间,实现大容量可逆隐藏.文献[24]提出了一种基于图像块分组的加密域可逆信息隐藏算法.该算法通过流密码异或加密图像,随后将密文图像分块,并对图像块分组,再根据秘密信息修改每组中相应图像块,从而实现信息隐藏.最近,文献[25]利用同态乘法和直方图平移技术将秘密信息嵌入密文图像;文献[26]运用同态乘法和密文分组技术实现在密文图像中隐藏信息;文献[27]根据游程编码的编码长度对密文图像块进行分类,然后根据图像块类型进行游程编码或二值矩阵压缩,从而腾出空间实现信息嵌入;文献[28]利用像素高位信息将密文图像块分为平滑区域和复杂区域两种类型,然后压缩平滑图像块的位平面,在腾出的空间中嵌入信息.
考虑到传统图像插值方法计算密文图像的插值结果时,其生成的直方图并非近似均匀分布,用这类插值图像作为信息隐藏的载体会引起监听者的注意,降低信息隐藏系统的安全性.为此,针对密文域图像信息隐藏应用,本文提出一种面向密文图像信息隐藏的随机插值方法.该方法计算得到的密文插值图像,其直方图近似均匀分布,具有较好的安全性.对比实验结果表明本文随机插值方法的安全性能比其他3 种文献插值方法都好.
1 本文的随机插值方法
传统图像插值技术有最近邻插值、双线性插值和双三次插值等.近年,一些研究人员利用图像插值方法[29-31]设计了多种明文图像信息隐藏技术,这些隐藏技术在插值像素中嵌入信息,实现了大容量隐藏和图像无损恢复.常用的插值方法有相邻均值插值(neighbor mean interpolation, NMI)方法[29]、相邻像素插值(interpolation by neighboring pixels, INP)方法[30]和相邻像素最大化差值的插值(interpolation by maximizing the difference values between neighboring pixels, IMNP)方法[31].这些插值方法在明文图像信息隐藏方面取得了较好效果,但并不适用于密文图像信息隐藏.其主要原因是,常用图像加密算法生成的密文图像,其直方图近似均匀分布,然而采用上述插值方法对密文图像进行操作却不能保持该特性.如果采用这类密文插值图像作为信息隐藏的载体,可能会引起攻击者的注意从而降低信息隐藏算法的安全性.
针对密文域图像信息隐藏应用,本文提出一种密文图像随机插值方法.该方法生成的密文图像的插值图像,其直方图近似均匀分布,具有较高的安全性.本文的密文图像随机插值方法共有以下7 个步骤:
步骤1生成初始插值图像,其长和宽分别为密文图像的两倍,设置伪随机函数的种子;
步骤2用密文图像的像素直接填充插值图像的奇数行和奇数列;
步骤3计算奇数行和偶数列的像素时(最后一列的像素除外),用其左右两个像素进行随机插值;
步骤4计算偶数行和奇数列的像素时(最后一行的像素除外),用其上下两个像素进行随机插值;
步骤5计算偶数行和偶数列的像素时(位于最后一行且最后一列的像素除外),确定其4 个对角像素的最大值和最小值,根据随机数的取值对最大值或最小值进行随机扰动插值;
步骤6计算最后一列的像素时,随机选取该像素所在行的一个像素进行填充;
步骤7计算最后一行的像素时,随机选取该像素所在列的一个像素进行填充.
如图1 为本文插值方法的流程图.上述步骤的详细计算过程如下:

图1 本文随机插值方法的框图Figure 1 Block diagram of the proposed random interpolation method
步骤1初始化插值图像和伪随机函数.假设I是大小为H ×W的密文图像,它生成一幅2H×2W大小的插值图像E,其中E的所有像素初始化为零.设置伪随机函数的种子为密钥S,由伪随机函数生成的随机数的取值范围为[0, 1].
步骤2计算奇数行和奇数列的像素.设I的第i+1 行和第j+1 列的像素为I(i,j),其中0iH −1 和0jW −1;E的第s+1 行和第t+1 列的像素为E(s,t),其中0s2H −1 和0t2W −1,然后执行赋值E(2i,2j)=I(i,j),其中0iH −1 和0jW −1.
步骤3计算奇数行和偶数列的像素(最后一列的像素除外).采用随机数服从均匀分布的伪随机函数生成随机数w1,接着进行插值计算E(2i,2j+1) = Rd(E(2i,2j)×w1+E(2i,2j+2)×(1−w1)),其中0iH −1 和0jW −2,Rd(·)代表向最近整数取整的函数.
步骤4计算偶数行和奇数列的像素(最后一行的像素除外).由伪随机函数生成随机数w2,然后进行插值计算E(2i+1,2j) = Rd(E(2i,2j)×w2+E(2i+2,2j)×(1−w2)),其中0iH −2 和0jW −1.
步骤5计算偶数行和偶数列的像素(位于最后一行且最后一列的像素除外).计算Q1= min{E(2i,2j),E(2i+2,2j), E(2i,2j+2), E(2i+2,2j+2)}和Q2= max{E(2i,2j),E(2i+2,2j), E(2i,2j+2), E(2i+2,2j+2)},其中min{}和max{}分别表示最小值和最大值函数.采用伪随机函数生成随机数w3,计算随机扰动值r1= Rd(P1× w3) 和r2= Rd((255−P2)w3),采用伪随机函数生成随机数w4,若0w4<0.15,则E(2i+1,2j+1) =Q1−r1;若0.15w4<0.4,则E(2i+1,2j+1) =Q1;若0.4w4<0.5,则E(2i+1,2j+1)=mod(Q1+r1,256);若0.5w4<0.6,则E(2i+1,2j+1)=abs(Q2−r2);若0.6w4<0.85,则E(2i+1,2j+1)=Q2;若0.85w41.0,则E(2i+1,2j+1)=Q2+r2,其中mod(,)代表取模函数,abs()代表取绝对值函数,0iH −2 和0jW −2.
步骤6计算最后一列的像素.由伪随机函数生成随机数w5,令k= mod(Rd(w5×248),2W −1),接着执行赋值E(i,2W −1)=E(i,k),其中0i2H −2.
步骤7计算最后一行的像素.由伪随机函数生成随机数w6,令k= mod(Rd(w6×248),2M −1),接着执行赋值E(2H −1,j)=E(k,j),其中0j2W −1.
下面举例说明本文随机插值的过程.如图2(a)所示,原始2×2 图像块中的4 个像素分别为I(0,0) = 51、I(0,1) = 8、I(1,0) = 135 和I(1,1) = 201,根据步骤2 计算得到像素E(0,0) = 51、E(0,2) = 8、E(2,0) = 135 和E(2,2) = 201,如图2(b)所示.对于这个原始图像块,由伪随机函数生成4 个值在[0,1] 的随机数a、b、c和d,假设它们的取值为a= 0.121 2,b= 0.315 5,c= 0.413 3 和d= 0.621 2,根据上述计算方法得到E(0,1) = Rd(0.121 2×51 + (1−0.121 2)×8) = 13,E(2,1) = Rd(0.315 5×135 +(1−0.315 5)×201) = 180,E(1,0) = Rd(0.413 3×51+(1−0.413 3)×135) = 100 和E(1,2)=Rd(0.621 2×8+(1−0.621 2)×201)=81,而对于E(1,1)取值,假设此时服从均匀分布的伪随机函数生成的随机数为0.315 3,属于区间[0.15, 0.40),则根据步骤5 可知,它的值取E(0,0)、E(0,2)、E(2,0)和E(2,2)中的最小值8.

图2 随机插值示意图Figure 2 Diagram of random interpolation
2 实验结果
为验证本文插值方法的性能,选取10 幅标准图像作为测试数据进行实验.如图3 所示,这些图像均为灰度图像,尺寸为512×512.

图3 标准图像Figure 3 Standard images
2.1 插值图像的视觉效果分析
为了验证本文插值方法的有效性,选择常用的Logistic 混沌映射[3]来生成密文图像.Logistic 混沌映射定义为

式中,µ为混沌控制参数.本文实验选取迭代初始值x0与µ作为Logistic 混沌系统的密钥.加密图像时,先利用式(1)迭代计算得到一个混沌矩阵C= (Ci,j)M×N,然后将矩阵元素值映射到[0, 255]区间,公式为
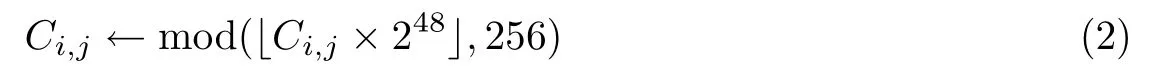

式中,⊕为对应元素异或操作.该图像加密方法的解密过程与加密过程类似,即在密钥控制下由式(1)和(2)生成混沌矩阵C,通过对密文图像与混沌矩阵C进行异或操作便可解密图像.利用Logistic 混沌映射加密得到的密文图像,其图像内容为无任何视觉意义的噪声图像且直方图近似均匀分布.
实验中,先对10 幅标准测试图像进行Logistic 混沌映射加密,接着用本文方法对密文图像进行计算.观察实验结果发现,本文方法生成的插值图像仍然是无视觉意义的噪声图像,安全性较好.限于篇幅,仅选择一幅纹理图像(Baboon)和一幅平滑图像(Girl)进行举例说明.图4(a)和图5(a)是Baboon 和Girl 的原图,图4(b)和图5(b)是利用Logistic 混沌映射加密得到的Baboon 和Girl 的密文图像,图4(c)和图5(c)是将本文随机插值方法分别应用于图4(b)和图5(b)而得到的随机插值图像.观察图4(c)和图5(c)发现,它们均为无视觉意义的噪声图像,说明本文随机插值方法在视觉效果方面具有较好的安全性.

图4 Baboon 原图、密文图像及其随机插值结果Figure 4 Original Baboon, its encrypted version and its random interpolated image
2.2 直方图对比实验

图5 Girl 原图、密文图像及其随机插值结果Figure 5 Original Girl, its encrypted version and its random interpolated image

图6 Baboon 密文图像的4 种插值结果的直方图对比Figure 6 Histogram comparison of the interpolated encrypted images of Baboon among four interpolation methods
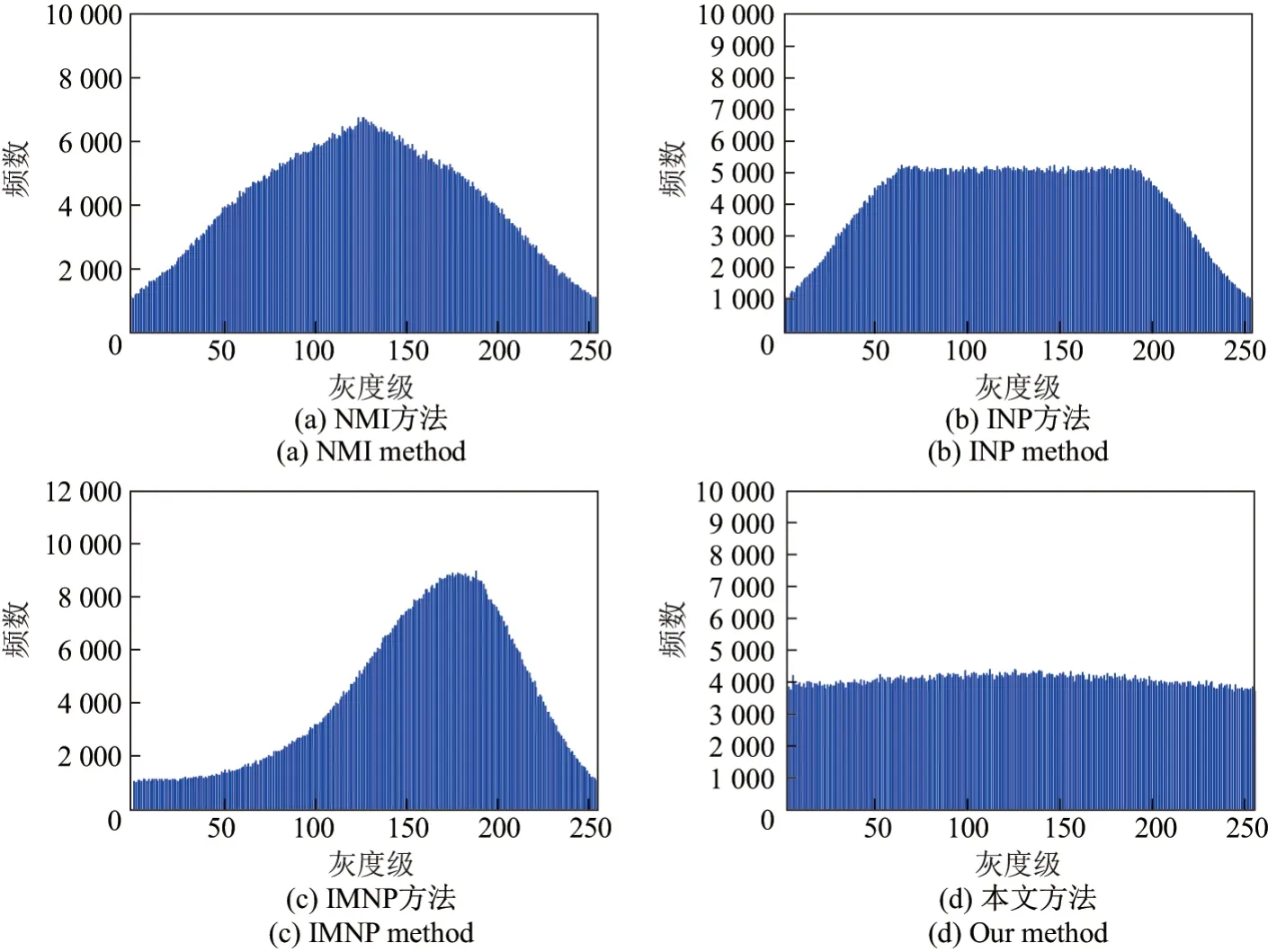
图7 Barbara 密文图像的4 种插值结果的直方图对比Figure 7 Histogram comparison of the interpolated encrypted images of Barbara among four interpolation methods
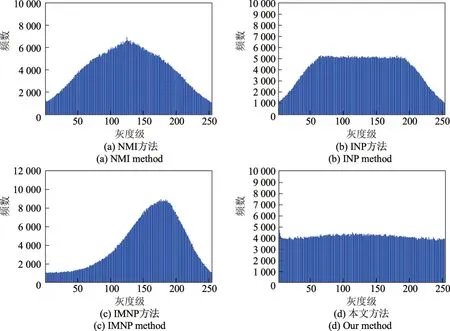
图8 Peppers 密文图像的4 种插值结果的直方图对比Figure 8 Histogram comparison of the interpolated encrypted images of Peppers among four interpolation methods
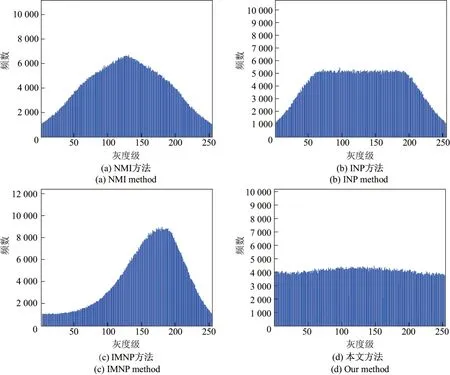
图9 Girl 密文图像的4 种插值结果的直方图对比Figure 9 Histogram comparison of the interpolated encrypted images of Girl among four interpolation methods
为了体现本文随机插值方法的优越性,与NMI 方法[29]、INP 方法[30]和IMNP 方法[31]等3 种方法生成的密文图像的插值图像直方图进行对比.限于篇幅,仅选择两幅纹理图像(Baboon 和Barbara)和两幅平滑图像(Peppers 和Girl)为例进行说明.图6∼9 列出了不同插值方法对这4 幅图像的密文图像计算得到的插值图像的直方图.对比结果显示,本文随机插值方法生成的插值图像直方图近似于均匀分布,而3 种文献对比方法的直方图并非均匀分布.由于常见图像加密算法生成的密文图像的直方图近似均匀分布,因此对于密文图像信息隐藏,选择本文方法的密文图像插值结果作为载体,其安全性要高于3 种文献对比方法.值得注意的是,对于不同密文图像,不同插值方法的插值结果的直方图分布均呈现相似性.这是因为Logistic 混沌映射加密不同输入图像时,其输出的密文图像的直方图均呈现近似均匀分布.换言之,尽管插值方法处理的密文图像所对应的原图不同,但这些密文图像的数据分布是相似的,因此导致最终输出的直方图结果具有相似性.
2.3 信息熵对比实验
信息熵[11]是判断图像安全性能的一种有效指标,反映了图像内容的随机程度,其计算公式为
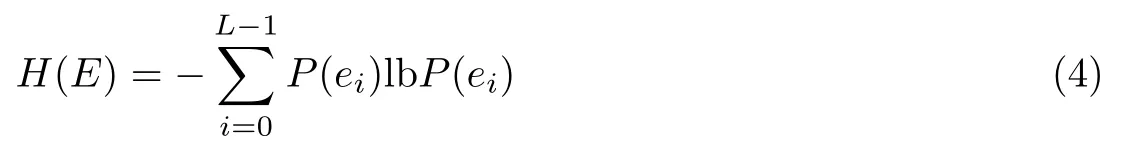
式中,E={e0,e1,··· ,eL−1},P(ei)是ei的发生概率.通常,信息熵的取值与密文图像的安全性正相关,即信息熵取值越大,密文图像的安全性越高.对于灰度密文图像,L=256,其信息熵的理论最大值是8.表1 是图像信息熵的计算结果,其中第2 列是密文图像的信息熵,第3∼6列是NMI 方法、INP 方法、IMNP 方法和本文方法计算得到的插值结果的信息熵.观察发现,本文方法的信息熵均大于3 种对比方法的信息熵,安全性更好.此外,本文方法的信息熵与密文图像的信息熵差异较小且接近理论最大值8.

表1 不同插值方法用于不同密文图像的插值结果的信息熵对比Table 1 Information entropy comparisons of the interpolated encrypted images generated by different interpolation methods
3 结 语
针对明文信息隐藏技术的插值方法在应用于密文图像隐藏时存在的安全性问题,本文利用随机分配插值权重的策略,设计了一种密文图像随机插值方法.由于本文方法可确保密文图像插值结果的直方图特性与常见图像加密算法的密文图像直方图特性保持一致,因此利用本文方法的插值结果作为密文图像信息隐藏的载体,具有较好的安全性.与基于插值方法的明文图像信息隐藏技术类似,一种可行的密文图像信息隐藏方案是通过密钥随机选取插值像素,然后将秘密比特随机嵌入到插值像素的1 个或多个位平面.对比实验结果表明,本文的随机插值方法在安全性方面优于3 种文献插值方法,具有一定的优越性.

