基于窄带干扰缓和技术的到达时间估计

金彦亮， 罗雪涛， 王 雪， 聂 宏

1.上海大学通信与信息工程学院，上海200444

2.北爱荷华大学科技学院，美国爱荷华州IA52242

近年来，无线室内定位技术越来越受到关注.针对无线环境的复杂性和特殊性，脉冲超宽带（impulse radio-ultra wideband, IR-UWB）信号因超宽的带宽、良好的时间分辨率以及无载波传输等特点而广泛应用于室内定位和测距[1-2].基于IR-UWB 的测距系统主要通过估计接收信号中直射路径（direct path, DP）信号的到达时间（time of arrival, TOA），进而计算出收发两端的距离.一般而言，基于多径检测的TOA 估计可分为使用匹配滤波的相干检测方法和基于能量检测（energy detection, ED）的非相干方法.其中，基于能量检测的非相干方法由于较低的实现复杂度而获得非常多的关注[3].

TOA 估计的准确度主要受到噪声、多径效应和干扰信号的影响.目前已知的许多TOA估计算法[4-6]在只有加性高斯白噪声（additive white Gaussian noise, AWGN）存在时可以达到很高的定位精度.但实际环境中IR-UWB 信号频带内可能存在着多个窄带无线通信系统，因此接收信号会受这些高强度的窄带信号干扰，使DP 信号检测和TOA 估计算法的性能大大降低.

为了缓和窄带干扰（narrowband interference,NBI）对IR-UWB 通信系统的影响，研究者提出了多种信号处理技术.文献[7]研究了数字干扰消除技术，该技术中接收信号必须通过模数转换器（analogue-to-digital conversion, ADC）转化为数字信号，但其采样率非常高，并不适用于低复杂度、低能耗的基于能量检测的接收机.文献[8]提出的模拟陷波滤波器组技术是另外一种传统的NBI 缓和技术.然而，使用模拟滤波器时很难改变其陷波频率，且不易获得窄带干扰的先验知识，故该技术并没有得到实际应用.文献[9]提出了一种结合Teager-Kaiser算子（Teager-Kaiser operator, TKO）和高通滤波器（high pass filter, HPF）的NBI 抑制方案，首先采用TKO 将NBI 移至接近直流（direct current, DC）分量的频带范围内，然后用高通滤波器滤除.目前已存在的TKO 的实现方法中大多数都是基于数字领域.为了处理IR-UWB 信号，TKO 的实施带宽至少为500 MHZ，数字实现方式复杂.受到TKO 技术的启发，文献[10]提出了一种基于平方律（square law, SL）器件和带通滤波器（band pass filter, BPF）的平方滤波技术，该技术用SL 和BPF 来代替TKO 和HPF，不仅可以获得良好的性能，而且特别适用于基于ED 的接收机.文献[11]将平方滤波技术[10]应用于IEEE 802.15.6 协议[12]IR-UWB物理层，以提升IR-UWB 通信系统存在NBI 时的同步性能，而文献[13]将平方滤波技术应用于UWB信号归一化非线性检测器的设计，以缓和NBI对通信系统误码率的影响，但是目前还没有将该技术用于IR-UWB系统TOA 估计中的研究.

本文将平方滤波应用于TOA 估计，分别在IEEE 802.15.4a CM3 视距信道和CM4 非视距信道[14]下研究并比较了在TOA 估计时采用平方滤波技术的能量检测方法和传统能量检测法性能的差异.

1 系统模型

本节主要从接收信号和接收机两方面介绍了基于IR-UWB 信号的TOA 估计系统.在发射端，采用多个脉冲作为发射信号.为了便于衡量不同方法的性能差异，采用统一的信道模型—IEEE 802.15.4a 信道[14].所产生的信道脉冲响应与发射信号卷积后加入高斯白噪声和窄带干扰形成接收信号.在接收端，分别采用传统的能量检测接收机和结合了平方滤波技术的能量检测接收机对接收信号进行处理，并完成到达时间的估计.

1.1 信号模型

在IR-UWB 系统中，发射端采用多个脉冲作为发射信号，而接收信号[15]可表示为

式中，a(t)为经过带通滤波器滤波后的IR-UWB 信号，n(t)为零均值、双边功率谱密度为N0/2的高斯白噪声，i(t)为窄带无线信号，N为发射的脉冲数；w(t)表示持续时间为Tp的IR-UWB单脉冲波形，(∗)为卷积运算，Tf为每一祯的持续时间.在每一帧中，发射脉冲前增加一个时间间隔τg，该时间间隔中同样只存在噪声干扰信号，可通过该区域来获得噪声或者干扰信号的相关信息；同时为了防止符号间干扰对TOA 估计的影响，在每一帧后增加一段持续时间为Tg的保护间隔，该保护间隔在发射信号中为空白区域，而在接收信号中为纯噪声干扰信号区域.h(t)为信道脉冲响应，表达式为

式中，{αl,τl}为第l条路径的衰减因子和延迟时间，L为路径数.在系统中可将窄带无线信号i(t)建模为一个广义平稳、零均值、高斯带通随机信号[16]，设Ri(τ)表示该随机信号的自相关函数，表达式为

式中，PI,fI,BI分别为NBI 的能量、中心频率和带宽.

1.2 接收机模型

图1 为传统的基于能量检测的接收机结构图，BPF 的带宽为B，中心频率为fc，其作用主要是为了消除带外噪声和干扰对系统性能的影响.经过带通滤波器的处理后，在平方器和积分器的作用下得到接收信号能量序列Vn,k，其表达式为

式中，n= 1,2,··· ,N,N代表发射脉冲的总数；k= 1,2,··· ,kg,··· ,K,kg==；Vn,k表示第n帧第k个能量采样；Tint为积分周期，在仿真中与单脉冲持续时间Tp相同.之后，利用IR-UWB 信号与噪声干扰信号采样能量分布的差异，对Vn,k实施到达时间估计算法获得用于直射路径（direct path, DP）检测的TOA 估计序列，设定阈值，在估计序列中第一个超过阈值的采样即为DP 信号.最终根据发射信号的结构以及每一帧已知的时间间隔τg计算IR-UWB 信号的到达时间.

图1 传统能量检测接收机的结构Figure 1 Structure of traditional energy detection receiver

由于ED 接收机无法从IR-UWB 信号中识别出噪声和干扰信号，在进行DP 信号检测和TOA 估计前需要对接收信号采用平方滤波技术[10]来消除窄带干扰对TOA 估计的影响.图2为应用了平方滤波技术的ED 接收机结构图.BPF1 的带宽为B，中心频率为fc，其作用与图1 中BPF 相同.通过BPF1 消除带外噪声和干扰后，将平方滤波技术应用于接收信号.该技术由一个平方器和带通滤波器BPF2 构成，BPF2 带宽为B −BI，频带范围为[BI,B]，通过平方器将接收信号中的窄带干扰分量平移至频带范围中的直流（direct current, DC）分量中，并利用BPF2 将其滤除，之后输出信号y(t)与传统ED 接收机一样利用平方器和积分器获得接收信号的能量采样序列Vn,k，实施TOA 估计算法获得估计序列，设定阈值进行DP 的检测并计算信号的到达时间.

图2 结合平方滤波技术的能量检测接收机结构Figure 2 Structure of energy detection receiver combined with square filtering technology

2 存在窄带干扰时到达时间估计的CRLB

克拉美罗下限（cramer-rao lower bound, CRLB）作为TOA 估计的理论界限可以从理论分析的角度反映不同测距系统的性能[17].系统的CRLB 越小，TOA 估计性能就越好，估计精度就越高.通过文献[15]可知，只存在加性高斯白噪声时系统的克拉美罗下限为

式中，β为有效带宽，rSNR为信噪比（signal noise ratio, SNR）的值.

存在NBI 时，NBI 的能量比加性高斯白噪声的能量大得多.当分析NBI 对系统性能的影响时，可忽略噪声n(t)的效应.接收信号可重新表示为

式中，a(t −τ)为接收的IR-UWB 信号，τ为信号传播时间延迟，i(t)为窄带无线信号，被建模成零均值且方差为的高斯随机信号.假设M次TOA 估计都是相互独立的，r=[r1,··· ,rM]，a=[a1,··· ,aM]，i=[i1,··· ,iM]分别为接收信号r(t)、IR-UWB信号s(t −τ)和NBI 信号i(t)的采样向量，并且时间延迟的估计量τ为无偏估计，则关于τ的似然函数p(r|τ)可表示为

若样本数量M为无限大，则

式中，To为实验观察周期.对似然函数p(r|τ)两边求取对数可得

将式(9)等号两边同时对估计量τ求导

费歇尔信息矩阵（Fisher information matrix, FIM）F为

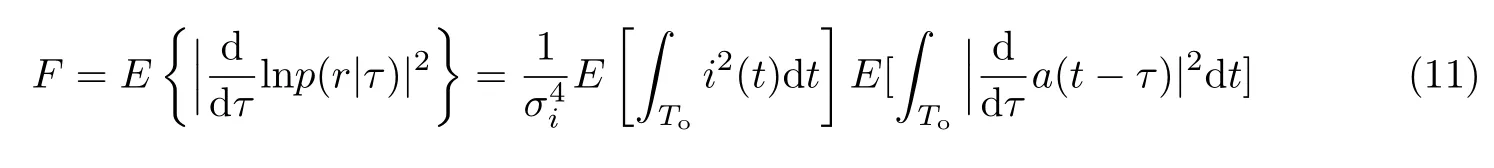
根据巴塞夫理论（Parseval’s relation）化简F可得

式中，A(f)为IR-UWB 信号的频谱.TOA 估计误差的方差不小于F的逆阵[15]，即

显然，存在窄带干扰时SIR 越大，测距系统TOA 估计的CRLB 越小，估计精度就越高.

3 窄带干扰缓和技术——平方滤波

BPF1 的输出信号r(t)经过平方器后，其结果可以表示为

图3 为经过平方器后输出信号的功率谱分布图.UWB 信号位于[0,B]和[2fc−B,2fc+B]频带范围内，NBI信号位于[0, BI]和[2fI−BI,2fI+BI]内，而交叉部分位于[0,|fc−fI|+(B+BI)/2]和[fc+fI−(B+BI)/2,fc+fI+(B+BI)/2]，所以当s(t)经过通带范围为[fp,B]的BPF2 滤波作用后，fp>BI的NBI 部分会被消除.BPF2 的频率响应表达式为

图3 平方技术后的接收信号功率谱Figure 3 Power spectrum of the received signal after Square Law processing

当存在NBI 时，由于NBI 信号强度较高，在分析过程中可将高斯白噪声的作用忽略掉.设Ep表示UWB 信号的功率，则在[0,TI]时间段内r(t)的SIR 值可表示为

经过平方滤波技术后的信号y(t)的SIR 值可表示为

根据文献[10]可知，由平方滤波技术所产生的SIR 增益可表示为

很明显I，GSL可以近似为

由于IR-UWB 信号频带十分宽，TI1，因此相对于传统的ED 接收机，使用了平方滤波技术的ED 接收机SIR 可得到极大的提高.根据式(14)可知，存在窄带干扰时SIR 值越大，TOA 估计精度就越高.所以，应用了平方滤波技术的IR-UWB 测距系统中TOA 估计精度更接近于测距系统的克拉美罗下限，可获得更高的TOA 估计精度.并且，该技术只需要提前对NBI 可能带宽BI进行估计，而不需要任何其他关于NBI的先验知识.

4 到达时间估计

为了研究采用了平方滤波技术的ED 接收机TOA 估计性能的提升，本文以文献[4]所提出的TOA 估计算法为主进行简单介绍.

步骤1利用式(4)得到Vn,k.

步骤2根据下式计算每一帧所对应的阈值ηn

式中，Q−1()为正态逆累积分布函数；µed和σed分别表示纯噪声区域中噪声采样的均值和标准差，可直接通过接收数据获得；pfa为虚警概率.当然这仅仅是一个十分粗略的阈值，主要利用该阈值来确定在大多数情况下DP 大于阈值的频率值.若采用的噪声信号符合高斯分布，则pfa值可设置得较高一点.通过步骤2 可知不同帧的噪声信号特性也不尽相同，故为了应对该问题应将阈值设定为自适应的.

步骤3将Vn,k与阈值ηn进行比较，利用式(22)得到新的序列Un,k，该步骤主要是为了将接受信号能量序列中大于阈值的采样点保留，小于阈值的采样点归零处理.

步骤4利用式(23)对Un,k进行累加处理得到Zk，Zk表示N帧中第k个采样TC（threshold crossing）事件发生的频率.

步骤5根据步骤4 获得Zk设定阈值ηz来检测首径信号.对于ηz并没有严格的限制，一般来说可将阈值设定为2N/3，因为在接收信号能量序列的噪声区域中每一列大部分采样点超过阈值的概率非常小.而与噪声区域相比，在存在IR-UWB 信号的区域每一列大部分采样点超过阈值的概率非常高.但是即使存在IR-UWB 信号时也并不是每一列的所有采样点都会超过阈值，所以若将阈值设定为每一列元素总数N或者最大值，则会导致检测错误.

5 仿真及讨论

本节分别在IEEE 802.15.4a CM3（line of sight, LOS）视距信道和CM4（non line of sight, NLOS）非视距信道[14]两种不同的环境中对传统基于能量检测的TOA 估计与应用了平方滤波技术的TOA 估计进行了仿真对比.在仿真实验中采用高斯脉冲的二阶导数(1−4πt2/θ2)e−2πt2/θ2作为发射脉冲波形w(t)，如图4 所示.其他各个参数具体设置见表1.

表1 参数设置Table 1 Parameters setting

信噪比为Ex/N0，其中Ex为每个脉冲的能量，均方根误差（root mean square error,RMSE）被用来分析不同能量检测方法TOA 估计性能的差异.每一个信噪比对应的RMSE 都是通过1 000 次仿真实验获得的.

本节首先在IEEE 802.15.4a CM3 视距信道下将两种能量检测接收机与文献[4]中TOA估计算法相结合，两种接收机的TOA 估计性能对比如图5 所示.其中，“ED”表示传统的能量检测方法，而“SL+BPF”代表应用了平方滤波技术的能量检测方法，设置rSIR=−6 dB，rSIR=−10 dB，rSIR=−15 dB，并在这3 种情况下进行对比分析.在视距环境中，当加入相对低强度NBI 时（rSIR=−6 dB），随着SNR 逐渐增大，两种接收方法的TOA 估计误差逐渐降低，当SNR 值大于15 dB 时，传统的能量检测方法RMSE 逐渐趋于稳定，高信噪比时最终估计误差仅仅稳定在2.8 ns 左右，无法满足人们对于室内定位和测距的要求.当应用平方滤波技术的能量检测方法时，RMSE 随SNR 的增大而下降，在高信噪比时误差稳定在0.5 ns.当加入相对高强度NBI 时（rSIR=−15 dB），采用传统能量检测法的IR-UWB 到达时间估计系统崩溃，随着SNR 的增大，估计误差并未明显的下降，而应用平方滤波技术后使得TOA 估计精度提升至0.9 ns.

图4 发射脉冲波形Figure 4 Transmitting pulse waveform

分析可知，RMSE 越低，系统的TOA 估计精度就越高，检测方法的性能就越好.平方滤波技术的应用使得接收信号的NBI 分量被平移至直流分量部分并被带通滤波器滤除，在接收机中提高了SIR，缓和了NBI 对接收信号能量分布的影响.接收信号中IR-UWB信号与纯噪声干扰信号的能量差异更加明显，更加有利于采用TOA 估计算法进行DP 信号的检测，最终系统的TOA 估计精度也得到大量的提升.

之后在IEEE 802.15.4a CM4 非视距信道下对比了两种能量检测接收方法TOA 估计性能的差异.如图6 所示，分别设置rSIR=−6 dB，rSIR=−10 dB，rSIR=−15 dB，很明显与同种情况的视距环境相比，非视距环境中两种接收方法的TOA 估计性能下降.当加入相对低强度NBI 时（rSIR=−6 dB），随着SNR 值逐渐增大，两种接收方法的估计误差逐渐降低，当SNR 大于15 dB 时传统的能量检测法RMSE 趋于稳定，最终稳定在6 ns 左右，在非视距和NBI 的双重影响下传统的能量检测法TOA 估计性能很差，而应用了平方滤波技术的能量检测法在高信噪比时最终RMSE 稳定在1 ns 左右，性能得到了很大的提升.当加入相对高强度NBI 时（rSIR=−15 dB），采用传统能量检测法的TOA 估计系统崩溃，耐受性很差，而应用平方滤波技术后，缓和了NBI 的影响，使得TOA 估计性能提升至2 ns.

分析可知，与视距环境相比，非视距环境中直射路径响应并非最大响应路径，接收信号中直射路径信号的能量降低，为TOA 估计实现高精度带来了困难.所以在非视距和NBI 的双重作用下，传统的能量检测法TOA 估计性能恶化十分严重；而应用平方滤波技术后在一定程度上减弱了NBI 的影响，虽然信道环境的改变使性能下降，但仍然优于传统的能量检测方法.

为了更明显地对比出两种接收机在存在窄带干扰时性能的差异，本节研究了固定信噪比时信道模型分别采用IEEE 802.15.4a CM3 和IEEE 802.15.4a CM4 两种接收机的TOA估计性能与加入窄带干扰强度的关系.仿真中设置rSNR=Ex/N0= 34 dB，rSIR变化范围为−15∼−6 dB.如图7 所示，随着rSIR的增大，无论是视距环境还是非视距环境，两种能量检测法的估计误差都逐渐降低，估计精度都逐渐提高.在视距环境下，应用平方滤波技术的ED 接收机在设定的rSIR变化范围内估计误差为0.5∼0.9 ns，而传统ED 接收机最低估计误差为2.8 ns 左右；在非视距环境下，应用平方滤波技术后误差可维持在1∼2 ns，而传统ED 接收机最低只能达到6 ns 左右.

分析可知，仿真环境中窄带干扰的强度对两种接收机TOA 估计精度有重要的影响，同样也从仿真层面说明了式(14)得到的系统克拉美罗下限与rSIR的关系：rSIR越大，系统的克拉美罗下限越低，TOA 估计性能越好.克拉美罗下限作为TOA 估计的理论界限可以从理论分析的角度反映两种系统的性能差异.理论分析结果与仿真相一致，说明应用了平方滤波技术的能量检测方法TOA 估计性能更好.

图5 IEEE 802.15.4a CM3 信道下两种接收机TOA 估计性能对比Figure 5 Performance comparison of two receivers’ TOA estimation under IEEE 802.15.4a CM3 channels

图6 IEEE 802.15.4a CM4 信道下两种接收机TOA 估计性能对比Figure 6 Performance comparison of two receivers’ TOA estimation under IEEE 802.15.4a CM4 channels

最后研究了设定不同采样率时，两种能量检测接收机在存在窄带干扰时的TOA 估计性能对比.如图8 所示，信道模型为IEEE 802.15.4a CM3 视距信道，rSIR=−6 dB，采样率fs分别设定为50 GHz 和25 GHz.显然，采用不同采样率时，应用了平方滤波技术的接收机和传统的能量检测接收机TOA 估计性能差异不大.并且，不论采样率高低，应用了平方滤波技术的接收机TOA 估计性能总是优于传统的能量检测法.本文所采用的平方滤波技术对窄带干扰的缓和作用在较低采样环境中同样有效，非常适合实际应用.

分析可知，在仿真实验中，设置不同采样率对于采用同种能量检测法区别仅仅在于收集信号能量的时间间隔不同.这种差异对于到达时间估计算法的整个过程并无太大影响.所以当采用不同采样率时同种能量检测法最终的性能差异不大.

图8 当rSIR=–6 dB 时不同采样率两种接收机的TOA 估计性能对比Figure 8 TOA estimation performance comparison of two receivers at different sampling rates under rSIR=–6 dB

6 结 语

本文研究了基于窄带干扰缓和技术的TOA 估计问题.将结合了平方律器件和带通滤波器的平方滤波技术应用于基于TOA 估计的超宽带定位和测距系统中，以缓和强窄带干扰对于TOA 估计算法性能的恶化.理论分析可知，在不需要任何关于窄带干扰先验知识的前提下，平方滤波技术可以极大地提高所接收的UWB 脉冲的SIR，并且存在窄带干扰时SIR 值越大，测距系统TOA 估计的精度就越高.之后在IEEE 802.15.4a CM3 视距信道和CM4 非视距信道下分别对存在NBI 的各种情况进行仿真.根据实验结果可知，在视距环境中，采用了平方滤波技术的能量检测方法在低强度NBI 下可达到0.5 ns 的估计精度，高强度NBI 下仍可维持在1 ns 左右的估计误差；在非视距环境中，采用平方滤波技术后在低强度NBI 时估计误差仍可降低至1 ns 左右，在高强度NBI 时也减缓了TOA 估计性能的恶化.因此，采用了平方滤波技术的能量检测方法具有更高的TOA 估计精度，更易于实现和实际应用.