植物组织微观结构变化的Mueller矩阵成像监测

刘 刚， 张亚丽， 赵静静， 王春华

上海大学特种光纤与光接入网重点实验室，上海200444

偏振信息可以反映被测样品内部分子的结构与排列信息，因此偏振信息测量已成为一种新型的检测手段，广泛应用于各学科领域，如材料研究以及生物医学研究等[1-5].一般来说，可以从样品的偏振信息中提取出微观结构特性[6].例如，退偏特性可以反映样品的散射程度[7].Mueller 矩阵能够全面描述被测样品的偏振信息，它是样品偏振特性的综合表征 .Mueller 矩阵能进一步提取出样品的退偏参数、相位延迟参数和二向色性参数等信息，因此常常作为介质极化表征的有力工具[9-10].

为表征植物样本的微观结构，本文提出一种双波片旋转测量法，并搭建后向散射Mueller矩阵成像系统.基于该系统测试植物组织样品的Mueller 矩阵的显微成像，展示植物叶片组织的Mueller 矩阵的特征.根据Lu-Chipman 的极化分解理论从Mueller 矩阵中提取出样本的极化参数，所得实验结果显示极化参数与样品的微观结构密切相关.为监测叶片组织内因缺水而导致的微观结构变化，借助Mueller 矩阵图像和极化分解技术系统地分析不同含水量下植物叶片组织的结构特征.对比Mueller 参数图与强度图可以发现，Mueller 矩阵元素和退偏参数可以更加显著地反映出植物组织样品因失水而导致微观结构的变化.Mueller 矩阵成像系统并没有破坏样品且测量操作简单，更具有监测植物组织微观结构变化的应用潜力.

1 系统与原理

1.1 后向散射Mueller 矩阵成像系统

本文采用双旋转波片法进行后向散射Mueller 矩阵偏振显微成像测量[11-12].系统装置水平放置，如图1 所示.光源采用功率为3 W 的红光面阵LED，其中心波长为632 nm.LED 发出的光经过准直透镜L1 变为平行光，再通过线性偏振片P1 和1/4 波片R1 所组成的起偏模块进行偏振调制.调制后的偏振光经过消偏振分光棱镜NPBS 后分成两束光，其中透射光经过10 倍物镜Objective 聚焦到样品上，然后由样品后向散射返回到Objective 放大变为平行光，再经过NPBS 反射后进入探测光路，最后由1/4 波片R2 和线性偏振片P2 所组成的检偏模块进行检偏后通过成像透镜L2 在CMOS 上成像.

在测量样品Mueller 矩阵的过程中，需要多次调制样品前后入射光和出射光的偏振态.实验测量时，首先将P1 和P2 固定，使得其方位角均为0◦，然后通过旋转R1 实现偏振态调制.由于Mueller 矩阵具有16 个元素，最少需要16 次成像测量.经优化确定R1 的旋转方位角分别为16◦、56◦、124◦、164◦时，系统引入的旋转误差噪声最小.同时，对应每个入射偏振态，R2 最少需要旋转4 次，以解调出输出光的偏振态.同理，经优化计算可以得出结论：当R2 的旋转方位角分别为16◦、56◦、124◦、164◦时，引入的旋转测量误差最小.分别在有或者没有被测样品的情况下，由CMOS 相应地采集32 幅强度图像，进一步计算出被测样品的Mueller 矩阵.

图1 Mueller 矩阵偏振显微成像系统Figure 1 Polarization microscope imaging system based on Mueller matrix

1.2 Mueller 矩阵测量原理

斯托克斯-Mueller 法则一般用于描述任意偏振态的光与器件相互作用后出射光偏振态的计算，若斯托克斯矢量为Sin的光入射到光学元件后出射光的斯托克斯矢量为Sout，则它们之间的关系可表示为

式中，M是样品的Mueller 矩阵，为4×4 矩阵，它广泛应用在偏振传输中.对于由一系列光学器件组成的光学系统来说，按照光束的传输顺序可直接将系统的Mueller 矩阵以多个器件的Mueller 矩阵进行级联乘积来表示.

在图1 所示的光路系统中，首先将偏振片P1 和P2 的方位角固定为0◦，其Mueller 矩阵分别用MP1和MP2表示，1/4 波片R1 和R2 的方位角分别记为θ1和θ2，其Mueller 矩阵分别用MR1和MR2表示，被测样品的Mueller 矩阵用Ssample表示，出射光经过R2 后的斯托克斯矢量用Scmos表示，则

于是可以将式(2)表示成

式中，A=MP2MR2,MP2和MR2分别表示为[13]

根据CMOS 相机所获得的光强值为斯托克斯矢量Scmos的第1 个分量即能得到1 个方程.因此，将R2 旋转4 次后通过测量4 组光强值可计算得到Sout，其计算公式为

式中，ai表示第i次（i=1，2，3，4）旋转R2 对应矩阵A的第1 行元素，Ii表示相应CMOS 相机所获得的光强值.根据式(6)列出4 个方程组，经验证可知方程组线性无关，进而求解出Sout.为求得经过样品后的4 组斯托克斯矢量Sout，需要将R1 旋转4 次.由式(1)可知，求解Mueller 矩阵需要4 个对应的Sin.

若不放置样品，即被测样品为空气，其Mueller 矩阵为单位矩阵E，则式(2)可表示为

因此，当被测物为空气时，可以旋转4 次R2 进行测量，根据式(6)即可得到入射光的斯托克斯矢量Sin.由式(1)将4 个Sin以及对应Sout联立，可得到16 个线性无关的方程组，进而获得样品的Mueller 矩阵Ssample中的所有元素.

1.3 Mueller 矩阵的分解

在本文实验中，首先对Mueller 矩阵元素进行分析，这16 个元素涵盖了样品所有的偏振信息，但每个元素所代表的物理意义并不明确.为了进一步对样品偏振特性进行定量分析，需要将Mueller 矩阵分解为能够反映样品结构信息或不同光学性质的偏振参数.目前，使用最广泛的Mueller 矩阵分解方法是由Lu 和Chipman 于1996 年提出的极化分解方法[14].该方法将Mueller 矩阵分解为3 个子矩阵的乘积，即描述器件退偏效应的矩阵M∆、描述器件双折射效应的矩阵MR、描述器件偏振衰减效应的矩阵MD.得到3 个子矩阵后，可以进一步对这些矩阵进行数学处理，从而获得相应的偏振参数[6,15].首先，将样品的退偏参数∆定义为

对分解所得的MR进一步处理可获得样品的总相位延迟参数R，它表示线性双折射和圆双折射的综合，其表达式为

并且还可以继续从MR中进一步处理得到圆偏振延迟参数RC

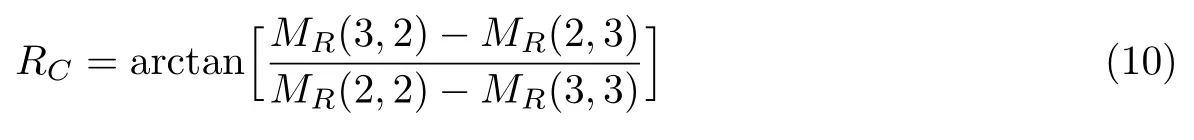
此外，样品的二向衰减参数D表示为

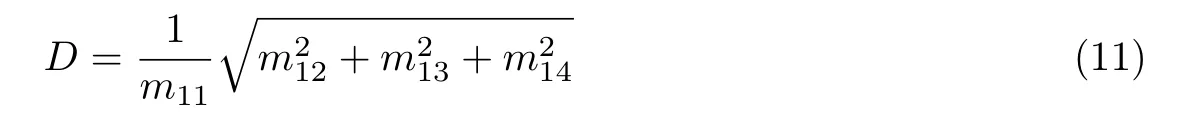
式中，m11、m12、m13、m14分别为样品Mueller 矩阵第1 行的4 个元素.

1.4 系统装置误差分析与校准

根据图1 可以发现：系统装置关于光源的稳定性、偏振片、1/4 波片以及CMOS 相机等多方面因素可能造成系统装置误差.为保证测量结果的可靠性，需要对Mueller 矩阵偏振成像系统进行误差测试分析，以减少这些误差给测量结果带来的影响.对Mueller 矩阵参量已知的样品进行检测，可以实现对成像系统的误差校准.图2 给出了1/4 波片（方位角设置为60◦）后向散射Mueller 矩阵校准后的结果，可以发现1/4 波片Mueller 矩阵参数的测量值与理论值基本吻合，该结果验证了Mueller 矩阵偏振成像系统在误差校准后的可行性.

图2 1/4 波片后向散射Mueller 矩阵Figure 2 Backscattering Mueller matrices of quarter waveplate

2 实验结果与分析

2.1 后向散射Mueller 矩阵元素表示的特征

本文选择了含水量较为丰富且易采集的绿萝叶片作为测量的组织样品，该植物组织样品的实验结果如图3 所示.其中，图3(a)为CMOS 采集的绿萝叶片组织样品的强度图，图3(b)为绿萝叶片组织样品的后向散射Mueller 矩阵图，对其所有元素相对m11进行归一化处理.首先，可以从图3(b)中看到绿萝叶片组织的Mueller 矩阵的非对角元素不为0，其中Mueller 矩阵元素m23、m32、m34、m43的绝对值较大，均大于0.25，并且对角元素m22和m33的大小明显不相等，这一特征表明绿萝叶片组织为各向异性介质.已有的研究结果指出：随着样品的各向异性程度的增加，m22和m33之间的差异以及非对角元素的大小也会增加[16].纤维散射体和光学双折射均会导致各向异性[17]：对于纤维散射体引起的各向异性，其m12、m21、m13、m31元素呈现周期性强度变化（m12=m21,m13=m31）；而对于双折射引起的各向异性，其m24、m42、m34、m43也会呈现周期性强度变化（m24=−m42,m34=−m43）.对比图3(b)中这些元素的特征可以发现，元素m12与m21、m13与m31的强度相似，这一现象表明绿萝叶片组织样品的各向异性主要是由样品的散射导致的.除此之外，

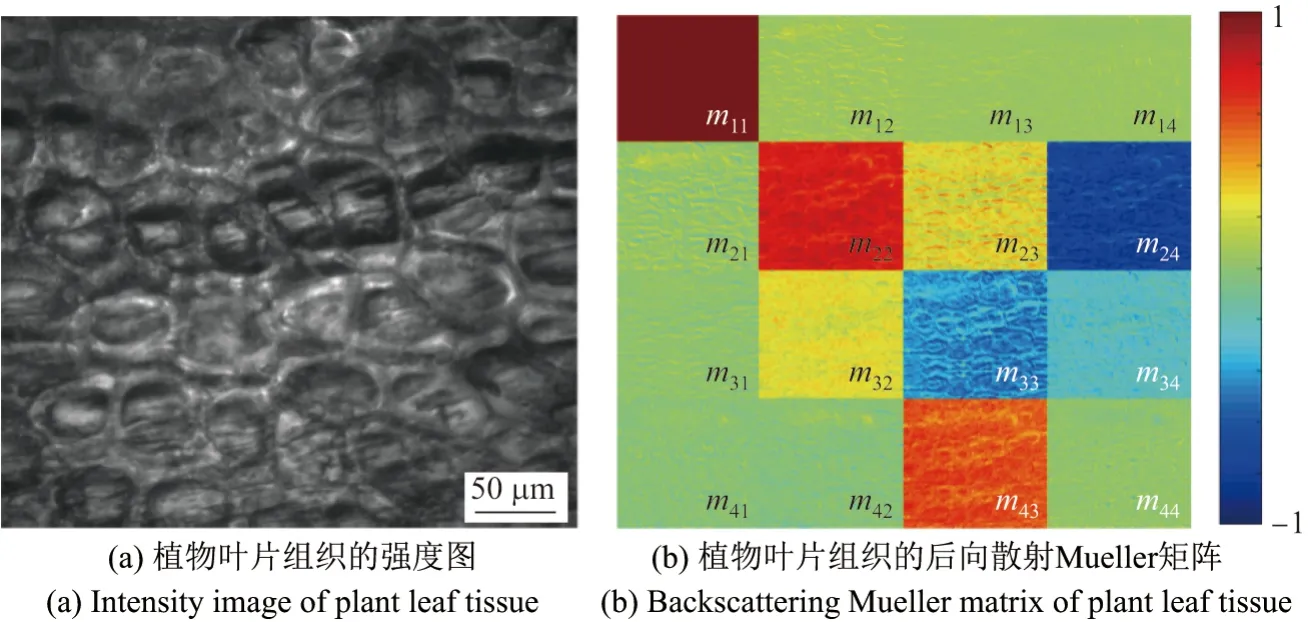
图3 植物叶片组织样品的实验结果Figure 3 Experimental results of plant leaf tissue sample

对角元素m22、m33、m44的强度与样品的退偏有关[18]，而且m22、m33的强度明显大于m44的强度，这是因为m22、m33与介质的保持线偏振能力相关.Mueller 矩阵中第1 行元素m12、m13、m14体现的是偏振衰减特性，与样品的吸收能力有关.第1 行元素的值约为0，这表明绿萝叶片组织的偏振吸收能力很弱.

2.2 Mueller 矩阵分解的极化参数表示的特征

本节将1.3 节中提到的极化分解参数应用于植物叶片组织.图4 为绿萝叶片组织样品的Mueller 矩阵分解参数图，从图4(a)中可以看到，绿萝叶片组织样品的退偏参数值不全为0，部分区域的退偏值达到了0.5 左右.因为该区域组织的细胞排列和形状不同于其他区域，所以散射程度不一样，进而说明样品的退偏与它们的轮廓以及内部结构差异有关，这一特性可用于获取植物叶片组织的边界及微观结构信息.图4(b)给出了绿萝叶片组织样品的圆偏振延迟参数.该参数反映旋光特性，而旋光特性又与糖的质量分数有关[19]，可以看到红色箭头所指区域的绝对值明显小于其他区域的数值，反映了绿萝叶片组织内不同区域的糖的质量分数不同.图4(c)显示了绿萝叶片组织样品的二向色性参数值在大部分区域均为0，体现了叶片组织内的衰减特性基本一致.

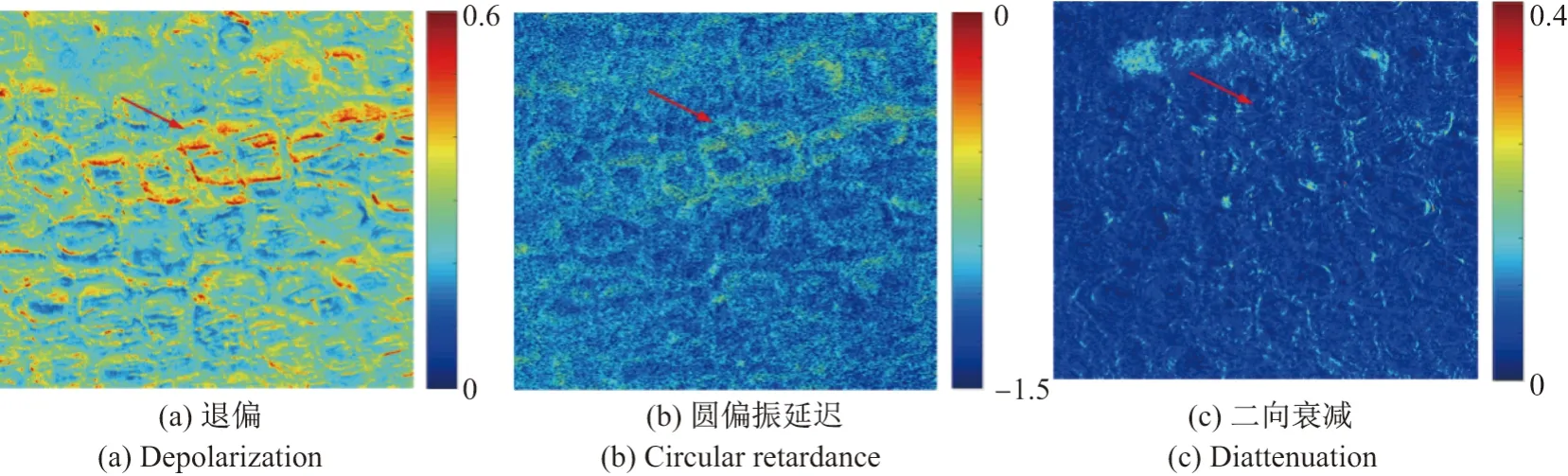
图4 植物叶片组织的Mueller 矩阵极化分解Figure 4 Mueller matrix polar decomposition of plant leaf tissue

2.3 不同实验时间下绿萝叶片组织的微结构变化特征

为了监测叶片组织内的微观结构变化，本文测量了在不同实验时间下的绿萝叶片组织样品.在0 h、4 h、8 h、12 h 情况下，绿萝叶片组织样品的Mueller 矩阵图像分别如图5 中的(a)∼(d)所示.从图5 中可以看出：随着实验时间的增加，Mueller 矩阵部分元素发生了明显变化.对角元素m22、m33、m44的变化，表明绿萝叶片组织样品的散射退偏的能力随实验时间的增加而变化，正好可以说明Mueller 矩阵元素能够反映组织样品的微观结构变化，而这些变化是由植物组织内含水量不同引起的.

根据2.1 中的讨论可以得出，Mueller 矩阵元素的二维分布图像可以提供丰富的样本结构信息.由于植物叶片组织最独特的特性是各向异性程度和退偏能力，本节同样用极化分解参数去分析不同实验时间下绿萝叶片组织的微观结构变化.图6(a)分别给出了在0 h、4 h、8 h、12 h 情况下绿萝叶片组织样品的强度图像.在不同实验时间下，绿萝叶片组织样品的Mueller 矩阵分解参数分别如图6 中的(a)∼(d)所示.以红色虚线标记区域为例，可以看到图6(a)中不同实验时间下的强度图没有发生变化.从图6(b)中可以观察到，随着实验时间的增加，退偏参数值整体在变小.该区域退偏参数平均值依次为0.323、0.307、0.275、0.259，这是因为叶片内的含水量随着实验时间的增加而减少，这一实验结果说明绿萝叶片组织样品的散射退偏能力随着水分含量的变化总体上呈现一个正相关的关系.再看图6(c)和6(d)，在不同实验时间下，绿萝叶片组织样品的圆偏振延迟参数和二向衰减参数几乎没有变化，说明这两个极化参数不能体现出叶片内含水量的变化.

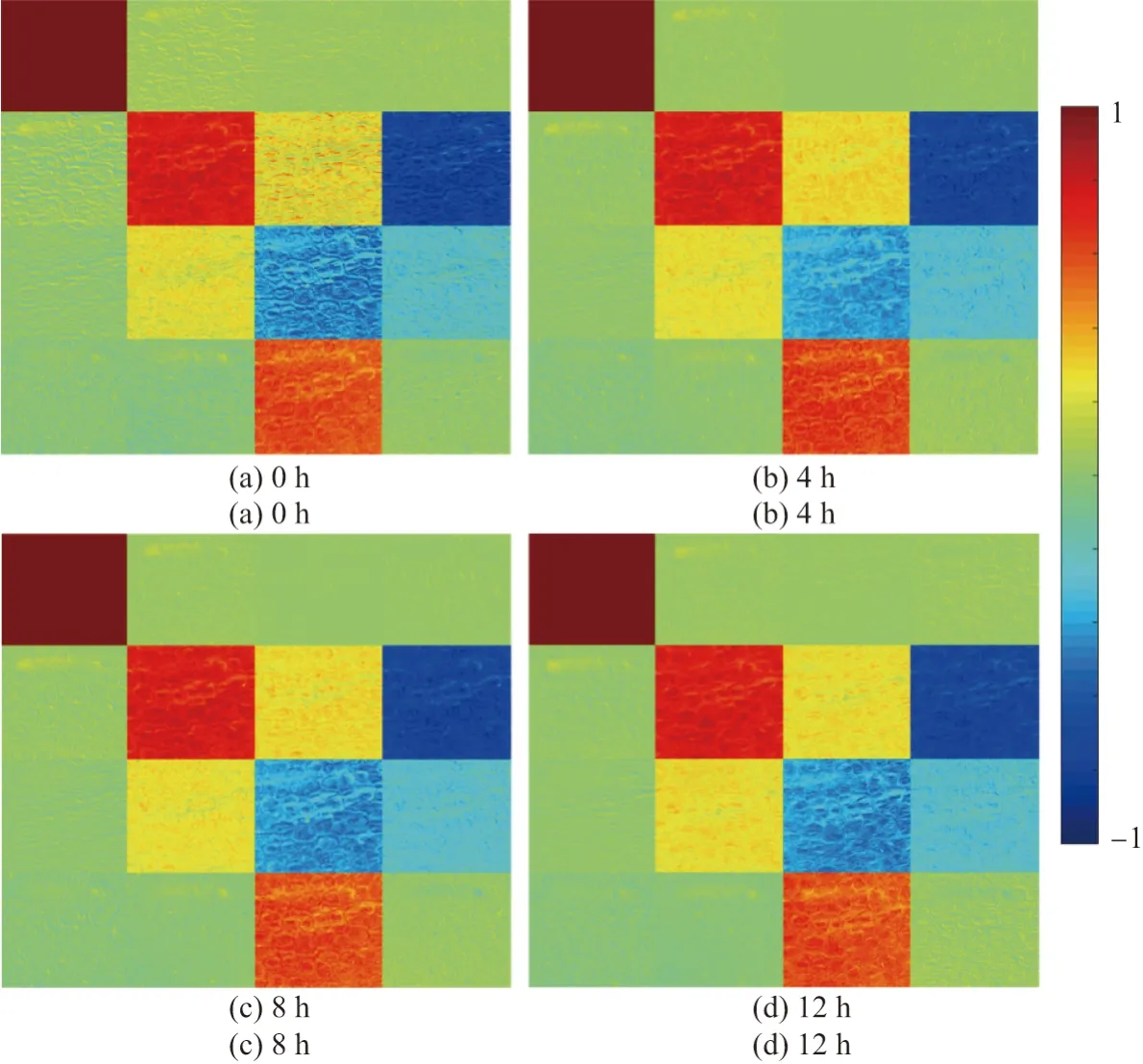
图5 不同实验时间下植物叶片组织样品后向散射Mueller 矩阵的实验结果Figure 5 Experimental results of backscattering Mueller matrices of plant leaf tissue sample at different experimental times

3 结 语

本文选择了一种含水量较为丰富且易采集的绿萝叶片作为本文测量的植物组织样品，并测量其后向散射Mueller 矩阵，分析了实验结果并总结了具有不同微观结构和光学性质的Mueller 矩阵的特征.首先，按照对角元素来区分是否为各向异性结构.其次，对角线的强度元素与样品的退偏能力密切相关.该实验结果表明，从样品的后向散射Mueller 矩阵中获取诸如各向异性程度、退偏以及吸收能力等不同的特征是可行的.此外，还利用Mueller 矩阵极化分解技术计算变换后的极化参数，定量地呈现植物组织的结构特征，进而得到样品更加丰富的微观结构信息.为了监测叶片组织内的微观结构变化，利用后向散射Mueller 矩阵二维分布图像和极化分解参数图分析不同含水量情况下植物叶片组织样品的结构特征.实验结果表明，Mueller 矩阵部分元素和退偏参数可以反映组织样品的微观结构变化.为了找出Mueller 矩阵参数和样品的微观结构特性之间更多的定量和精确的关系，仍需要对不同组织样品进行研究.

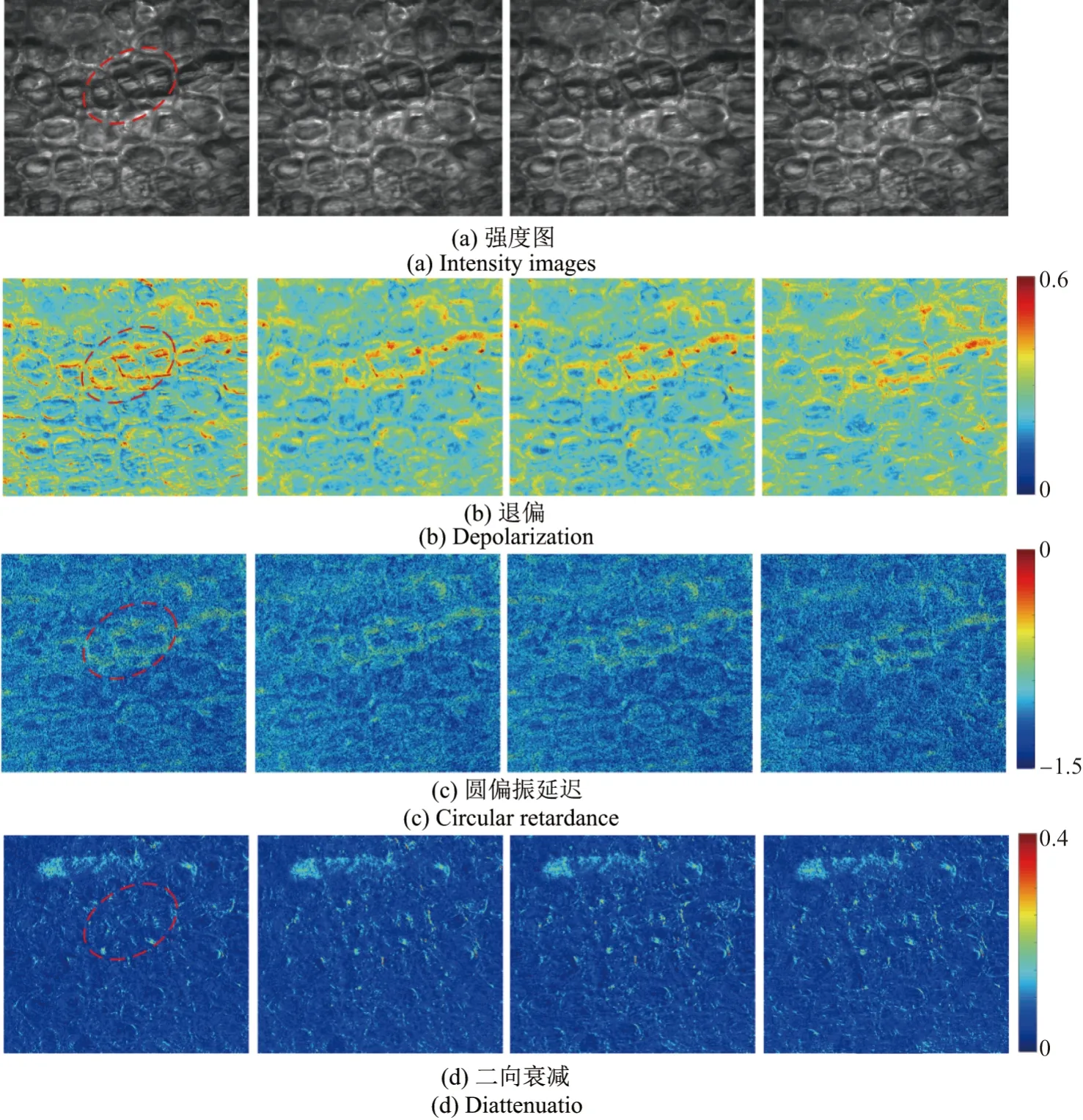
图6 不同实验时间下植物叶片组织样品的Mueller 矩阵分解参数图Figure 6 Mueller matrix polar decomposition imaging of plant tissue at different experimental times