辉绿岩单轴及常规三轴压缩下力学特性试验研究

沈 君，刘保国，程 寅，宋 宇，刘 浩，武 磊

(1.交通运输部科学研究院，北京 100029；2.北京交通大学土木建筑工程学院，北京 100044)

岩石或岩体在受力情况下的变形、屈服、破坏及破坏后的力学特征是岩石力学工程理论计算与设计的基础。近年来，对于岩石力学特性的研究主要集中于岩石的强度、变形、破坏及本构关系等领域，采用的研究方法分别有：理论分析、室内或现场原位试验和数值模拟，其中室内以岩样的单轴、常规三轴压缩试验和剪切试验等为主，为岩石力学与工程的设计、施工提供理论依据和工程指导。

在岩石工程领域中，如水利水电、边坡、地下工程和采矿工程等，中外学者已经开展较为全面系统的试验研究，并取得丰硕的研究成果。

在20世纪中叶，国外学者Wawersik等[1]针对脆性岩石开展室内压缩试验，主要分析脆性岩石在单轴压缩试验全过程曲线的两个基本类型及岩石的基本力学特征，初步揭示脆性岩石的破坏过程及机理。由于工程中遇到的岩体大部分均处于三向应力状态下，因而三向应力状态下岩石的强度和变形特性备受关注，如：Gowd等[2]选取了砂岩为研究对象，在刚性试验机上开展常规三轴压缩试验，得到砂岩的三轴脆-延转化特性。

在中国，对于岩石力学特性的研究已有较多成果，吴玉山等[3]选取多种岩石试样开展不同应变率条件下单轴压缩试验，主要分析岩石破坏后区的力学特性；文献[4-5]主要以大理岩和红砂岩试样为对象开展室内常规三轴压缩试验，较为系统地研究大理岩全应力-应变过程中的力学特性及本构关系。众多学者研究表明，岩石具有峰后残余强度，这是无可争辩的，它表示岩石破坏后，并不是完全丧失承载能力，而是仍然具有一定的强度，其中：陈庆敏等[6]选取某煤矿泥岩和砂岩为研究对象，开展室内常规三轴压缩试验，主要对岩石的残余强度与变形特性进行了研究，得出结论有：岩石残余强度是受结构控制的，随围压的变化表现出较强的敏感性；岩石在残余强度阶段的体积急剧膨胀，主要原因是各种微裂隙之间已相互贯通,逐渐形成了较大的宏观裂纹、裂隙并沿破裂面产生岩块间的相对滑动而造成的。杨圣奇等[7]研究了大理岩常规三轴压缩试验下强度和变形特性，分别对中、粗颗粒大理岩进行常规三轴压缩试验，试验结果表明：大理岩的峰值应变与围压成显著正线性关系；残余强度对围压的敏感性明显高于峰值强度。徐松林等[8]对岩爆现象进行分析，开展了大理岩等围压三轴压缩试验和峰前、峰后卸围压试验，分别对不同过程大理岩的强度和变形特性进行较为系统的研究，对于探明脆性岩石的破坏机理、岩爆产生等均有着重要的工程实践意义。文献[9-10]主要研究了具有垂直层理和水平层理岩样的各向异性力学特征，开展了单轴压缩、巴西劈裂及点荷载试验，揭示了岩样各向异性力学特性及破坏模式下力学机制。汪果等[11]分析英安岩的岩石力学特性及破裂损伤全过程中的声发射特征，结果表明随着围压的增大，其物理力学参数也增大，但未定量给出其增长规律关系。

因此，针对岩石力学参数随围压之间的定量变化关系及其离散程度这一研究不足，选取辉绿岩为研究对象，开展了室内单轴及常规三轴压缩试验，较全面地研究了辉绿岩的变形和强度特性及其力学参数离散程度分析，以期为相关的岩石(岩体)工程的设计、施工与支护提供理论依据。

1 试验准备

试验采用岩石为辉绿岩，取自某矿山巷道围岩，主要由辉石和基性长石组成，含少量橄榄石、黑云母、石英等。为保证岩石的完整性及一致性，所取岩样均来自同一区域岩石，用塑料密封包裹并运回试验室，岩样在采取、运输过程中未受到较大震动。利用室内摇臂钻床及数控磨石机将取得的岩样按照《工程岩体试验方法标准》加工成高径比(高度与直径之比)为2的试件，即高为100 mm，直径为 50 mm 的圆柱形试件。岩样的加工精度满足国际岩石力学学会建议试验规范要求，加工完成的辉绿岩岩样如图1所示，用游标卡尺测量的岩样尺寸如表1示。

图1 辉绿岩岩样

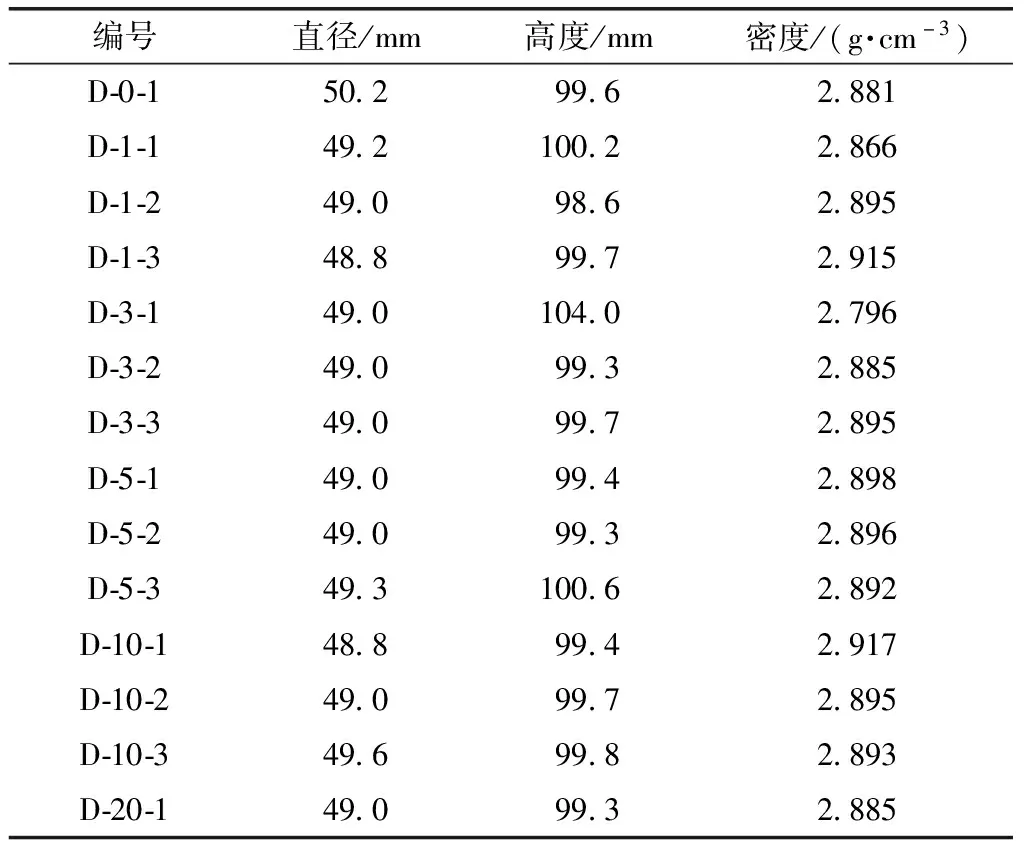
表1 岩样尺寸

注：编号中D表示辉绿岩(diabase)；X表示试验围压(MPa)；Y表示在X围压下进行的试件数目。

试验采用TAW-2000微机控制电液伺服岩石三轴试验机，如图2所示。

图2 TAW-2000岩石三轴试验机

2 试验数据分析

2.1 应力-应变关系曲线分析

利用Origin数据处理与绘图软件处理试验记录数据，绘制单轴及常规三轴压缩条件下轴向应力-轴向应变、径向应变-轴向应变及体积应变-轴向应变关系曲线。本试验规定取轴向应变ε1、径向应变ε2及体积应变εv压缩为正值、膨胀为负值，体积应变εv由式(1)计算，关系曲线分别如图3、图4所示。

εv=ε1+2ε2

(1)

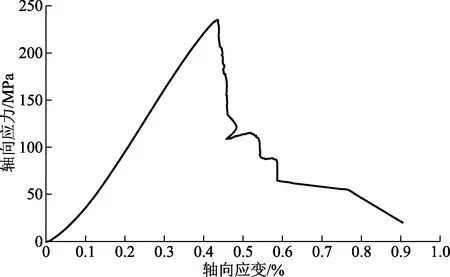
图3 单轴压缩条件下辉绿岩轴向应力-轴向应变关系曲线

由图3、图4可知，轴向应力-轴向应变关系曲线在轴向应力较小时均出现上凹趋势，随着轴向应力的逐渐增大变为直线上升，在达到峰值时均出现应力骤降，实验过程中可以听见清脆响亮的声音，说明岩样发生宏观上明显破裂，且峰后曲线均呈现出明显的台阶式跌落，同时由于围压的限制，第一次峰值应力跌落之后岩样不会直接丧失其承载能力，最终表现出应力值随轴向应变的增加而趋近于稳定值，即达到残余强度阶段。从径向应变和体积应变与轴向应变关系曲线可知，在岩样达到峰值强度之前，径向应变和体积应变变化特别小，但在峰值破坏瞬间出现了陡增，说明此刻岩样发生宏观破坏，最终稳定在体积应变大约为径向应变的2倍，其中，在围压为20 MPa时，体积应变和径向应变的值均较小，表明高围压条件下对岩样的侧向膨胀约束较好，证明了通过提高径向应力(围压)加固松散破裂围岩的方法是可行的。

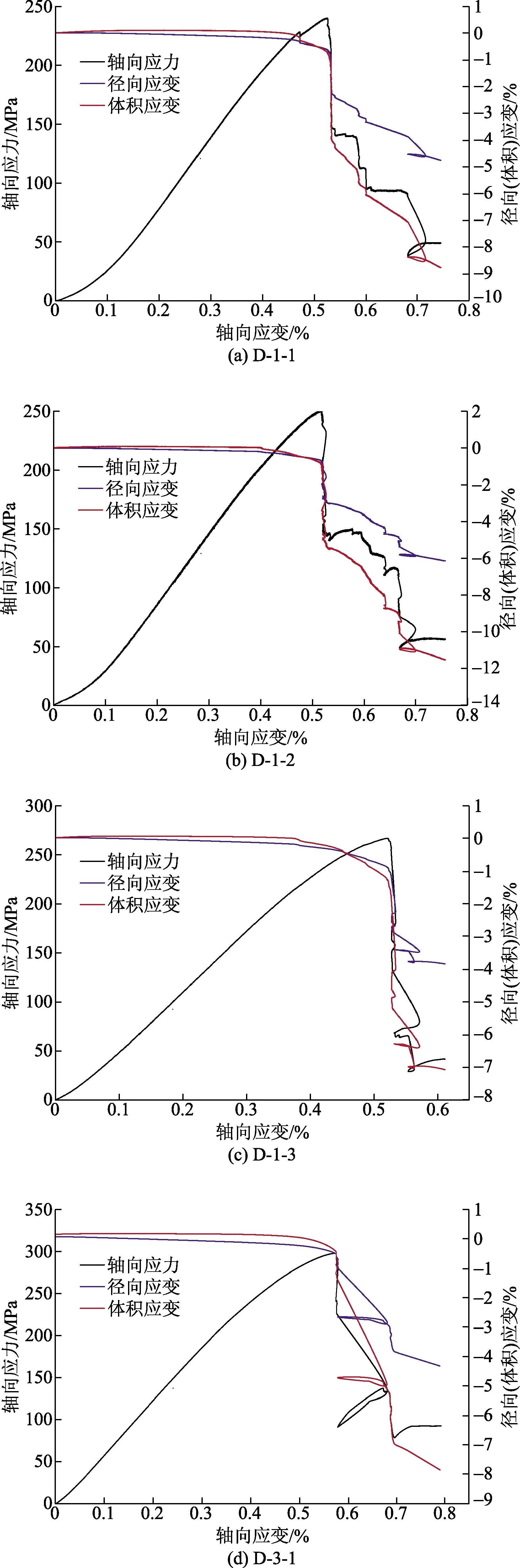
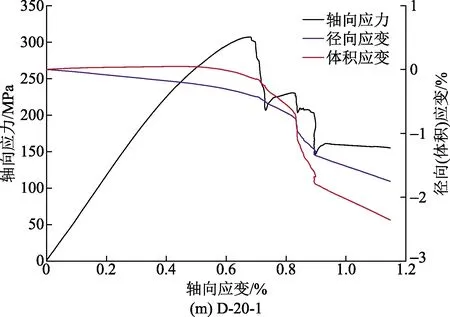
图4 常规三轴压缩条件下辉绿岩轴向应力、径向应变及体积应变与轴向应变关系曲线

2.2 基本物理力学参数计算

从应力-应变关系曲线中提取辉绿岩基本物理力学参数并进行计算整理，详见表2所示。由于在围压为1、3、5、10 MPa条件下各进行了3个试件，故取平均值来表征辉绿岩的物理力学参数，详见表3所示。

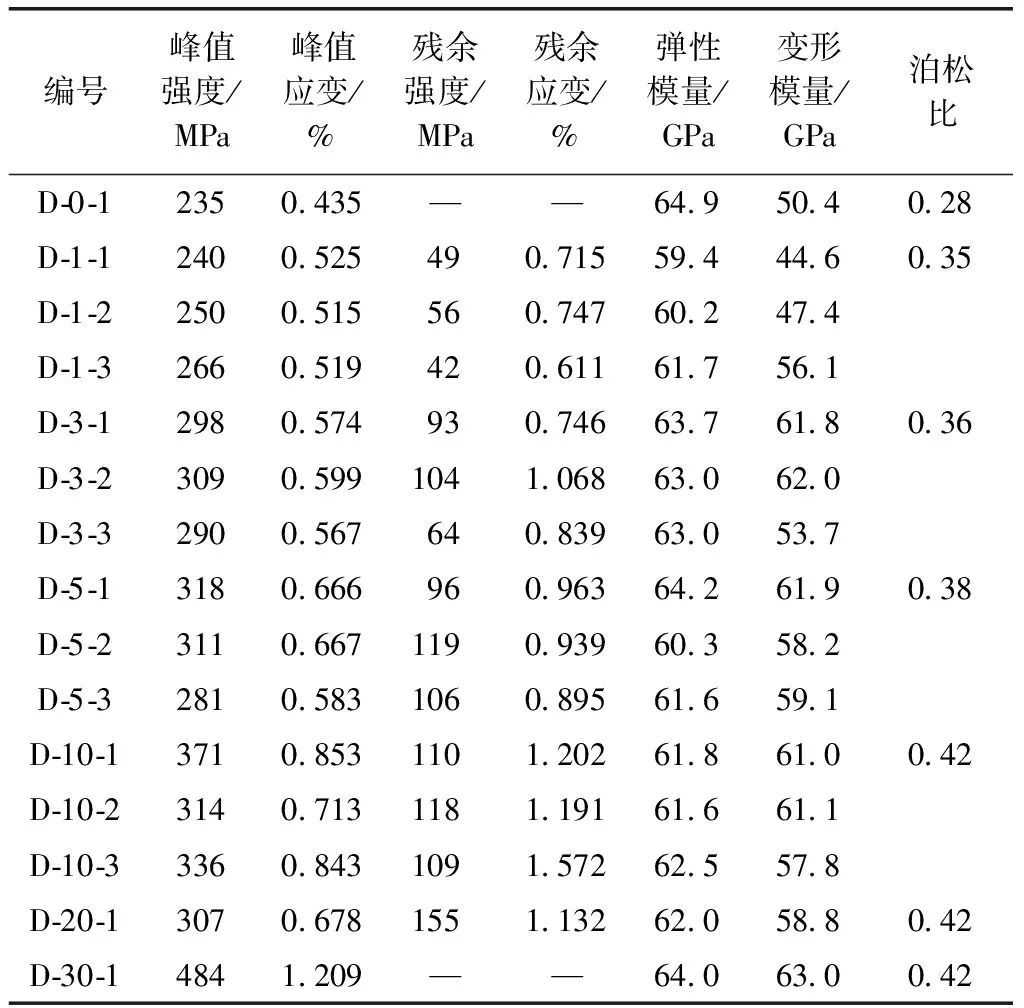
表2 辉绿岩基本物理力学参数

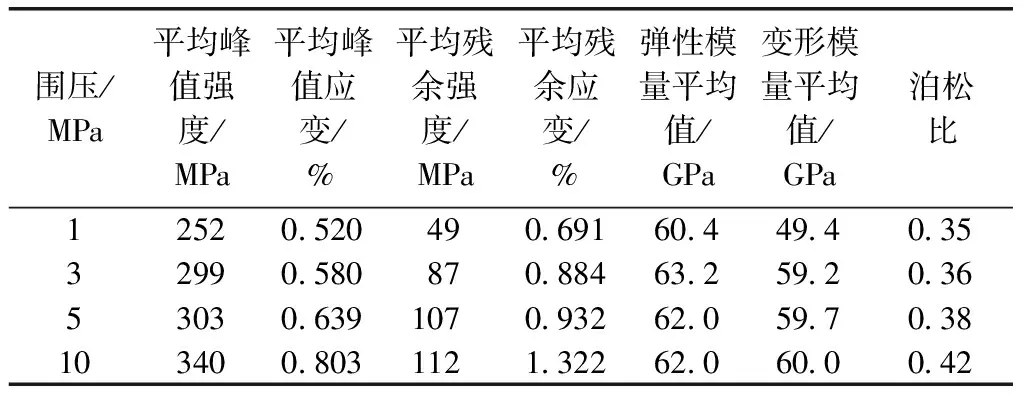
表3 辉绿岩基本物理力学参数平均值

由表2、表3可知，辉绿岩的峰值强度、峰值应变、残余强度、残余应变、弹性模量、变形模量和泊松比整体上均呈现出随围压的增大而增大的趋势。弹性模量的最小值为60.4 GPa，最大值为64.9 GPa，变形模量的最小值为49.4 GPa，最大值为63 GPa，泊松比的最小值为0.28，最大值为0.42，其中弹性模量和变形模量的最小值均出现在围压为1 MPa，而通过实验计算的泊松比值较地勘报告给出的泊松比大的原因主要是在试验时测量径向应变的链式引伸计置于试件的中间位置所致。

2.3 试样离散性分析

为了更加准确地分析辉绿岩在围压为1、3、5、10 MPa时力学参数的离散程度，故定义描述辉绿岩基本物理力学参数的离散程度用指标δ表征，具体计算式为

(2)

考虑到工程中常用到的岩石力学参数，此处仅计算辉绿岩峰值强度、残余强度、弹性模量和变形模量的离散程度，计算结果如表4所示。

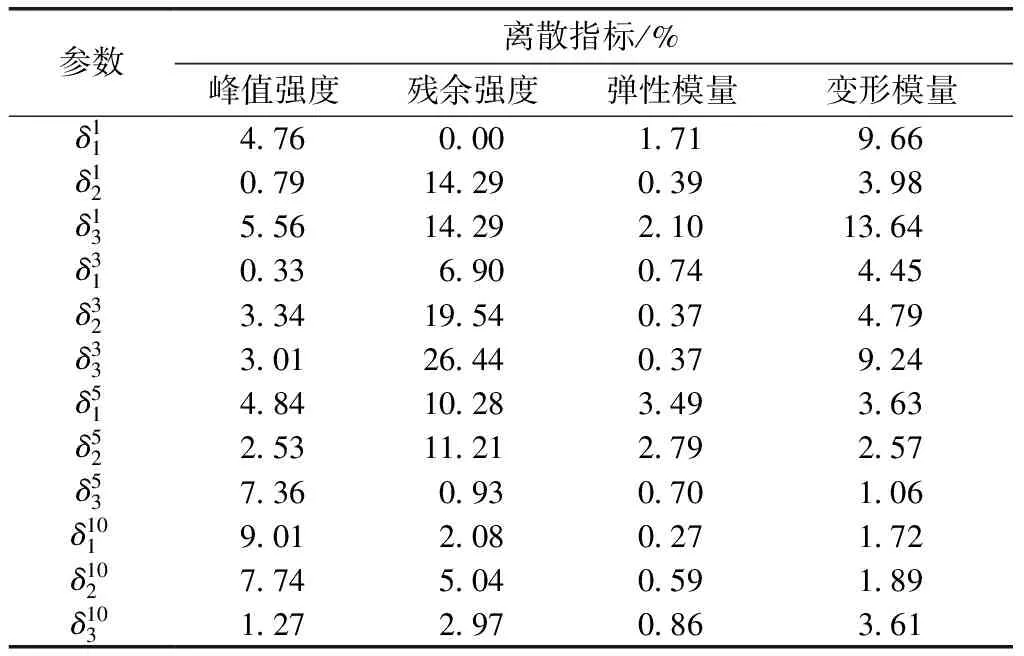
表4 辉绿岩力学参数离散程度

由表4可知，辉绿岩在围压为10 MPa时，其峰值强度最大离散程度的值约为9%，在围压3 MPa时达到最小值为0.33%，其值越大表示偏离平均值越大，离散性越强。残余强度的最大离散程度值为26.44%，最小值为0%，分别出现在围压为3 MPa和1 MPa时，主要原因是岩石的残余强度不仅与围压有关，更大程度上取决于试验时岩石破裂状态，是否能在围压的限制下破裂面进一步咬合继续承载，故岩石的瞬时破坏具有较强的随机性从而导致残余强度值存在较大的离散性。辉绿岩的峰值强度和残余强度具有不同程度的离散性，其中弹性模量的离散指标值较小，在0.27%～3.49%范围之间波动，故离散性较小，能较好地表征辉绿岩的变形特性。在围压为1 MPa时，变形模量的离散程度均较大，其最大值为13.64%，在围压为5 MPa时值最小，其最小值为1.06%。

整体而言，试验选取的辉绿岩离散程度较小，且符合基本的物理现象及规律，为研究其力学特性提供了可靠、有利的理论支撑。

3 辉绿岩变形特征分析

为了清楚地描述辉绿岩在不同围压条件下的变形规律，选取弹性模量、变形模量和泊松比为变形指标进行绘制曲线、拟合公式，并分析峰值应变和残余应变与围压的关系。

图5 弹性模量与围压的关系

通过对表2、表3中辉绿岩基本物理力学参数离散性较大的数据剔除，并以围压为横坐标，弹性模量、变形模量、泊松比、峰值应变和残余应变为纵坐标，绘制散点图并拟合曲线，分别如图5～图9所示。

图6 变形模量与围压的关系

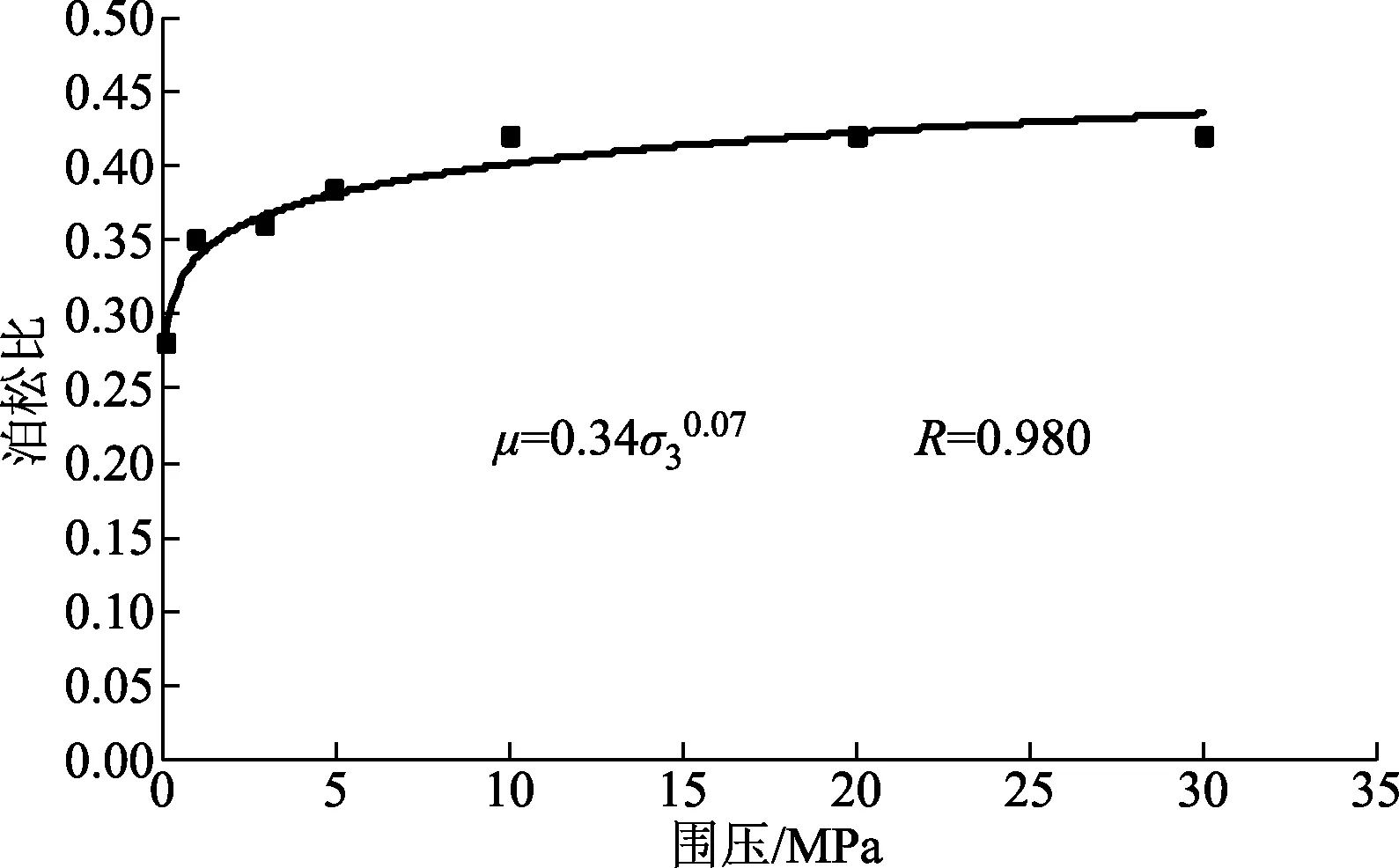
图7 岩样泊松比与围压的关系

图8 峰值应变与围压的关系

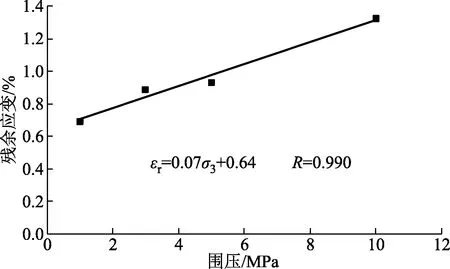
图9 残余应变与围压的关系

由图5～图7可知，随着围压的增大，辉绿岩的弹性模量、变形模量及泊松比均表现出较明显的非线性增长关系，均可以用幂函数形式进行拟合，当围压大于20 MPa时，辉绿岩的弹性模量和变形模量的差异逐渐减小，这主要是由于岩样微裂隙在高围压作用下逐渐闭合所致。但辉绿岩的弹性模量、变形模量和泊松比并不会随着围压的增大而无限增大，而是趋于一个稳定值。这一规律为隧道工程中不同地应力条件下准确选取弹性模量、泊松比等岩石力学参数提供了理论依据。

由图8、图9可知，此处的峰值应变和残余应变是指岩样在达到峰值强度和残余强度时所对应的轴向应变。围压越大，辉绿岩峰值(残余)应力附近峰值(残余)应变也越大，呈现显著正线性关系，线性公式拟合相关系数较高，可达到0.99。

4 辉绿岩强度特征分析

岩石的黏聚力C和内摩擦角φ是工程设计中十分重要的力学参数，关系着岩石工程设计与施工是否科学、安全，经济是否合理，同时也是分析岩石强度特征的两个关键指标。

利用库仑(Coulomb)强度准则进行回归分析，从而确定岩石的黏聚力C和内摩擦角φ。该准则中以最大主应力σ1f和围压σ3表示，具体公式(3)：

σ1f=b+aσ3

(3)

式(3)中：a和b均是强度准则参数，公式表征一个给定的岩样能够承载的最大轴向应力σ1f与围压σ3呈线性关系。a和b与黏聚力C和内摩擦角φ的关系如下：

(4)

(5)

通过对表2、表3中辉绿岩峰值强度和残余强度离散性较大的数据剔除，并以围压为横坐标，峰值强度和残余强度为纵坐标，绘制散点图并拟合曲线，分别如图10、图11所示。

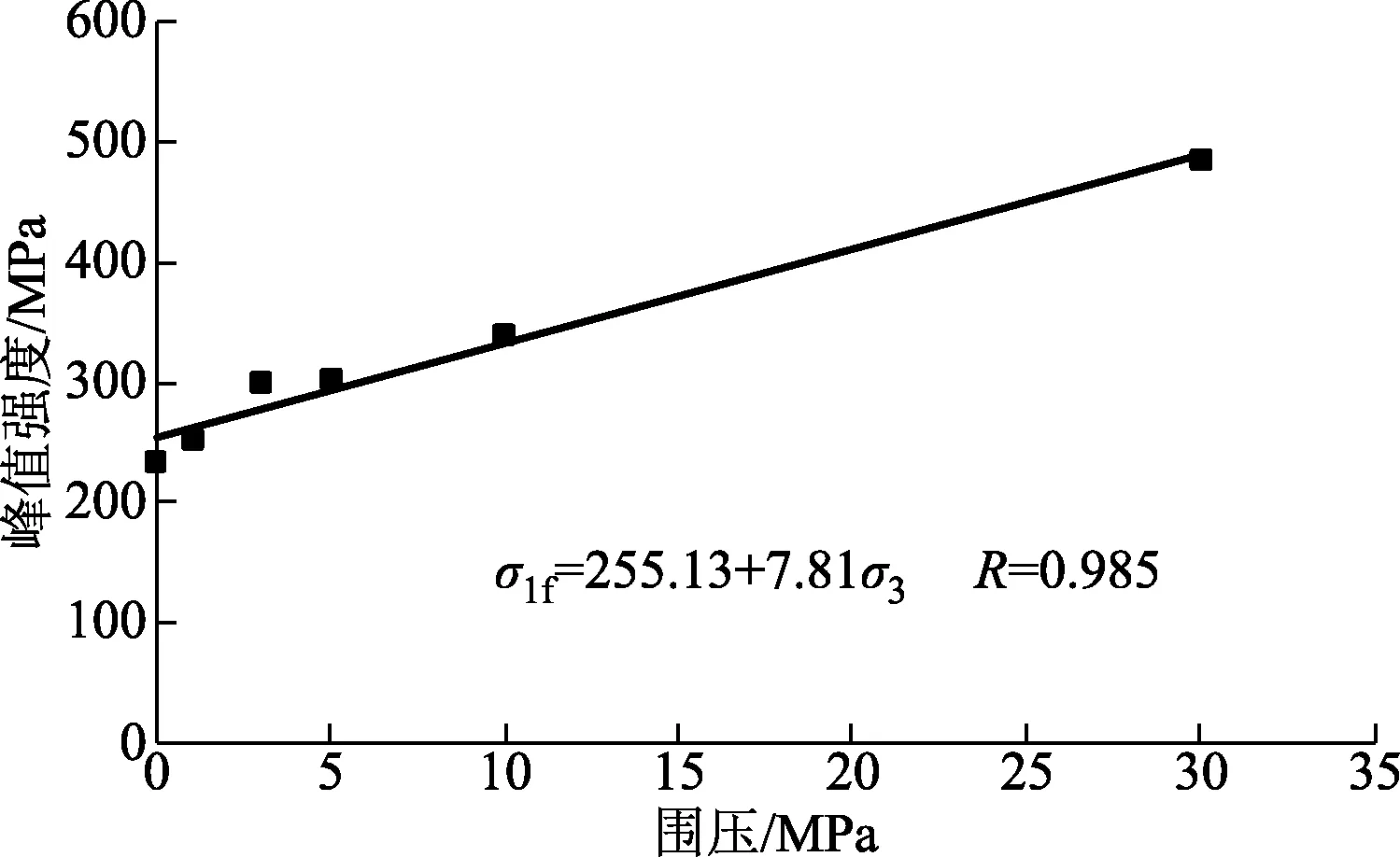
图10 峰值强度与围压的关系

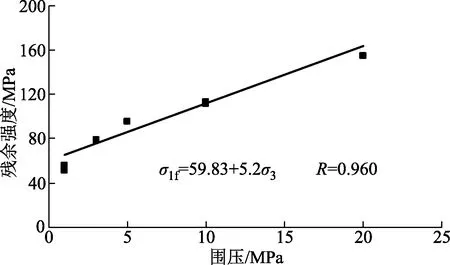
图11 残余强度与围压的关系

由图10、图11可知，随着围压的增大，辉绿岩的峰值强度和残余强度均呈现出较显著的正线性增长关系，均可以用一次函数形式进行拟合。岩样的实际单轴压缩强度为235 MPa比库仑准则中拟合的强度参数b=255 MPa(当围压为0时)稍微偏低，因此，为了得到更为真正围压对岩样强度特征影响规律，建议最好不使用单轴压缩强度的数据。通过残余强度-围压拟合的线性公式，不能表征围压为0时的残余强度值，因为在单轴压缩试验峰后破坏过程较为迅速，残余强度近似跌落至0。

由式(4)、式(5)计算得到辉绿岩的黏聚力C和内摩擦角φ，计算结果如表5所示。

表5 辉绿岩强度参数

由表5可知，在峰值强度处计算得到的黏聚力和内摩擦角分别为45.6 MPa、50.6°；在残余强度处计算得到的黏聚力显著低于由峰值强度计算得到的数值，仅为13.1 MPa，约为峰值时黏聚力的28%，内摩擦角为42.6°，约为峰值时内摩擦角的84%，主要是由于岩样在进入残余强度阶段已形成贯穿的宏观破裂面，此时黏聚力较低，但内摩擦角并没有显著减小，原因是：此处内摩擦角主要由沿岩样断裂面的多条粗糙不平整裂隙之间的咬合摩擦及岩样矿物颗粒自身提供承担。

5 结论

(1)辉绿岩的峰值应变、残余应变、弹性模量、变形模量和泊松比整体上均呈现出随围压增大而增大的趋势。其中，峰值应变和残余应变均呈显著的线性增长关系，可采用一次函数形式拟合；弹性模量、变形模量和泊松比均表现出较明显的非线性增长关系，可采用幂函数形式进行拟合，但并不会随着围压的增大而无限增大，而是趋于一个稳定值。这一规律为实际工程中不同地应力条件下准确选取弹性模量、泊松比等参数提供理论基础。

(2)定义描述辉绿岩基本物理力学参数的离散程度，分别计算辉绿岩峰值强度、残余强度、弹性模量和变形模量的离散程度指标，其中：弹性模量的离散指标值较小，在0.27%～3.49%波动，离散性较低，能较好地表征辉绿岩的变形特性。

(3)随着围压的增大，辉绿岩的峰值强度和残余强度均呈现出较显著的正线性增长关系，可采用一次函数形式拟合。在峰值强度处的黏聚力和内摩擦角分别为45.6 MPa、50.6°，在残余强度处的黏聚力显著低于由峰值强度计算得到的数值，仅为13.1 MPa，约为峰值时黏聚力的28%，内摩擦角为42.6°，约为峰值时内摩擦角的84%，黏聚力在峰后残余阶段降低显著，也是影响岩体稳定性的重要原因。