面向HBT干涉定位的直线式传感阵列结构优化

刘梦然，李善强，贾 雯，聂 磊

(湖北工业大学湖北省现代制造质量工程重点实验室,武汉 430068)

声学定位技术是声学、电学、信号处理等多门交叉学科的集成应用，广泛应用于军事、生活、工业检测等领域。目前，声学定位技术主要通过声传感器来获取声源信号，对采集的声源信号进行处理，从而确定声源的位置。声学定位的方法可以归纳为以下三类：基于到达时差法[1]、可控波束形成定位法[2-3]、基于声压幅度比定位法[4]。相比后面两类定位方法, 基于到达时差法的定位技术具有结构简单、计算量小等优点，应用较为广泛[5]。特别对于到达时差法，可基于光场HBT(Hanbury Brown and Twiss)干涉原理进行声场干涉目标定位，这种方法考察了信号之间的相关性，可排除无内禀相干性的干扰信号，因此能够实现在低信噪比情况下低频信号的远距离准确定位[6]。

经典的声传感器定位阵列拓扑结构有直线阵、十字阵、圆形阵和L型阵等结构。从几何上看，这些经典拓扑结构都可以看作直线阵列的延伸，而且直线阵具有加工简单、收放便利的优点，非常适合于各种载具的实际应用，因此直线阵列拓扑结构的研究具有非常重要的意义。现今众多学者针对定位传感阵列冗余问题开展了阵列优化研究[7-13]。

基于声场HBT干涉定位方法，设计了一种优化算法，以对声源的定位误差范围在1%以内为目标，对八元直线传感阵列进行了拓扑仿真优化；通过实验检测，筛选出了满足实际应用的直线阵列。

1 声场HBT干涉定位原理

声场HBT干涉理论来源于光场HBT干涉[14-15]，光的HBT干涉现象是由Hanbury Brown和Twiss在1956年提出的，测量恒星角直径的光强干涉仪即基于该原理设计而来。

实验室可见光波段的HBT实验原理图如图1所示。

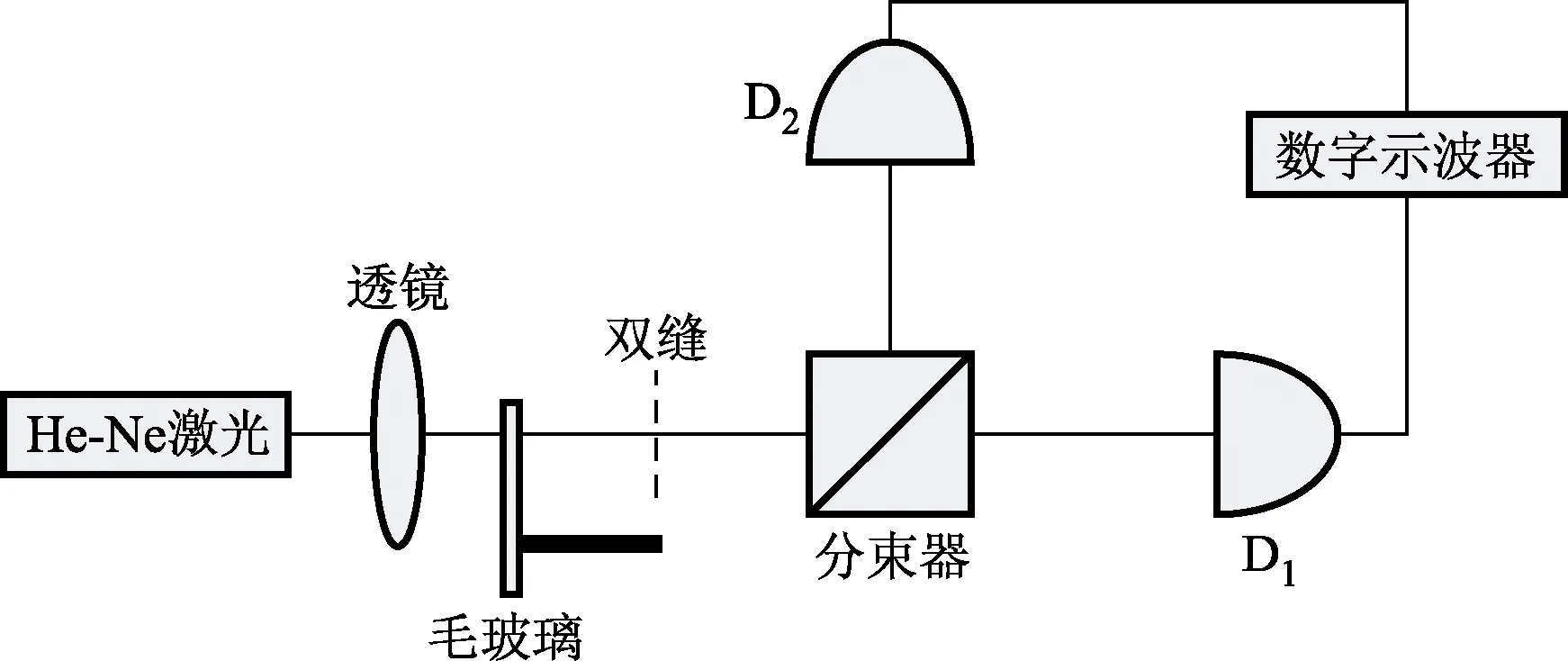
图1 可见光波段HBT实验原理图

He-Ne激光器发出激光经过旋转的毛玻璃，使其激光等效于一个空间波矢方向随机分布的热光源。通过一个双缝的光用一个50:50的分光镜分成垂直的两束光，用两个光电探测器采集光信号并进行强度测量。如若将D1探测器固定，然后对D2探测器进行横向扫描，从而通过数字示波器得到两个探测器光强值的强度归一化相关函数。

假设空间内以一个声源S作为坐标原点，同平面坐标系内存在声学传感器A和B，分别位于距离声源S半径为r1和r2处，传感器A和B接收声源发出的声波，接收信号分别为Q1(r1,t1)以及Q2(r2,t2)，如图2所示。

图2 声场HBT干涉实验示意图

根据光场中可见光波段实验的相干光计算，将光学二阶相关函数的计算方法引入到声学定位，可以得到任意两个传感器之间的相关函数G：

(1)

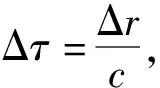
(2)

对8个传感器从左至右进行1～8排序，则八元传感阵列的相关函数为

G=G12G13G14…Gij…G78

(3)

式(3)中：Gij表示第i个传感器与第j个传感器的相关函数。

根据光场干涉特性，当频率、相位相同时，两束光发生干涉，即出现明暗相间的条纹变化情况，且零级条纹光强最大。同理，同一个声源发出一列声波信号，传感器A与传感器B接收信号的相对时间差为0时，信号的相干性最强，即两个传感器相关函数最大。因此，可以得出，使式(3)中G达到最大的坐标点位置，即为声源位置。

2 阵列结构优化方法与仿真分析

建立直角坐标系，8个传感器分别等距离放置在X轴上，组成直线阵列，如图3所示。假设声源位置放置(5 m，20 m)，运用MATLAB软件，通过直线阵列进行声源定位仿真模拟，通过扫描得到该扫描区域内所有相关函数，其中相关函数值最大的点即为声源坐标，如图4所示的八元阵列声源定位效果图，定位结果为(5 m，20 m)，与所设置声源坐标一致。

图3 八元直线传感阵列

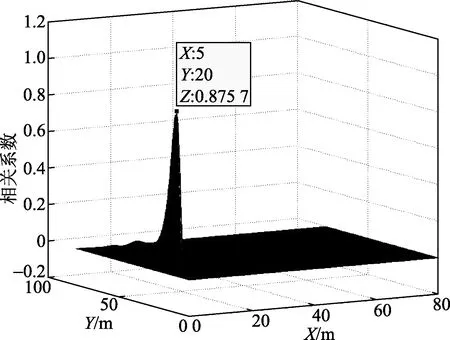
图4 八元阵列仿真定位结果图

根据本文所提出的以下优化算法对八元传感直线阵列进行优化，具体优化步骤如下：

(1)确立参数集。首先，采用二进制规则对阵元的存在状态进行编码，存在传感器为1，不存在传感器为0，例如10101000表示一、三、五这3个位置放置传感器。其次，根据声场HBT干涉定位原理，其至少需要3个传感器才能实现对声源的定位，则以传感器个数的不同在参数，建立传感器个数为3～7的5个优化阵列参数集。例如传感器存在个数为3的阵列如11100000、11010000、11001000等，放入第一个参数集。

(2)输出模型的确定。根据声场HBT干涉理论，以式(3)为目标输出模型，并计算其定位误差。

(3)停止条件确立。以传感器存在个数为3的参数集开始，依次对5个参数集进行仿真，得到每个阵列对应所定位出来的声源坐标。以阵列的定位误差在1%以内作为传统终止条件，当停止条件出现时，还需完成该参数集内剩下阵列的定位仿真。

(4)选出最优阵列。在满足阵列的定位误差在1%以内的参数集中进行筛选，选择出最优阵列。

(5)对最优阵列进行下一步验证，绘制出坐标与相关函数的仿真图像，观测其特征参数。

上述优化基本思想的具体流程如图5所示。

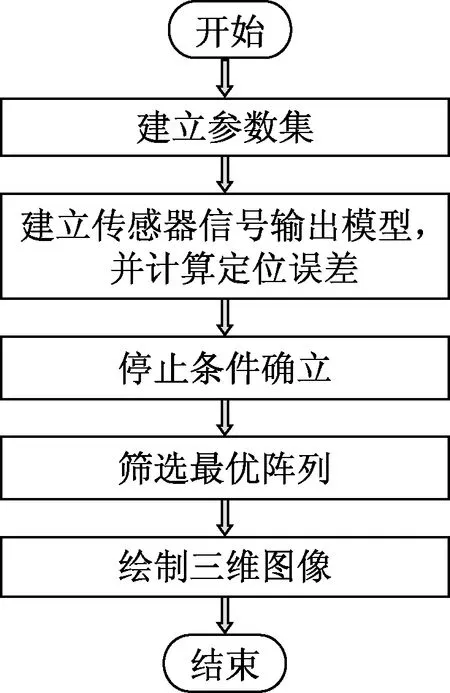
图5 阵列结构优化流程

根据阵列结构优化仿真，得到5种最优阵列分别为01100110、10100101、10101010、11000011、11001100，定位误差均为0.97%。其每种优化阵列对声源定位的三维仿真图如图6所示。

由以上仿真结果可以看出，优化后的5种四元传感阵列均可在减少传感器个数的前提下，满足定位误差在1%以内的定位效果。

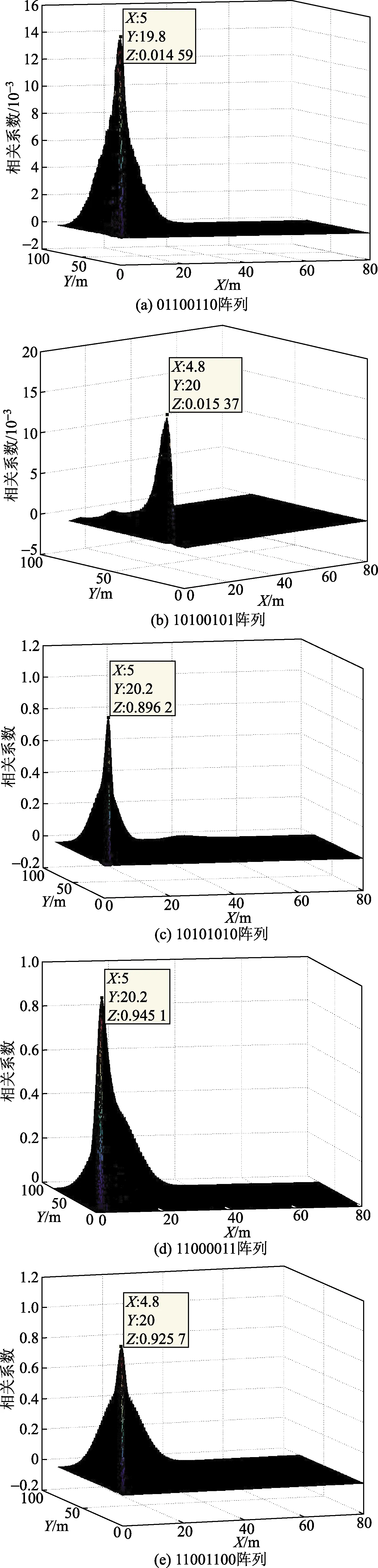
图6 最优阵列仿真定位三维图

3 阵列优化的测试实验及分析

对以上声源定位仿真得到的优化阵列进行实验验证，在实际测试中，八元直线阵列的声传感器以及声源摆放位置如图7所示，其中声源真实坐标为(5 m，20 m)，采用八元直线阵列传感器所实现的定位效果如图8所示。从图8中可以得到定位的声源位置在(5 m，20.2 m)，其定位误差为0.97%。

图7 声源定位实验图

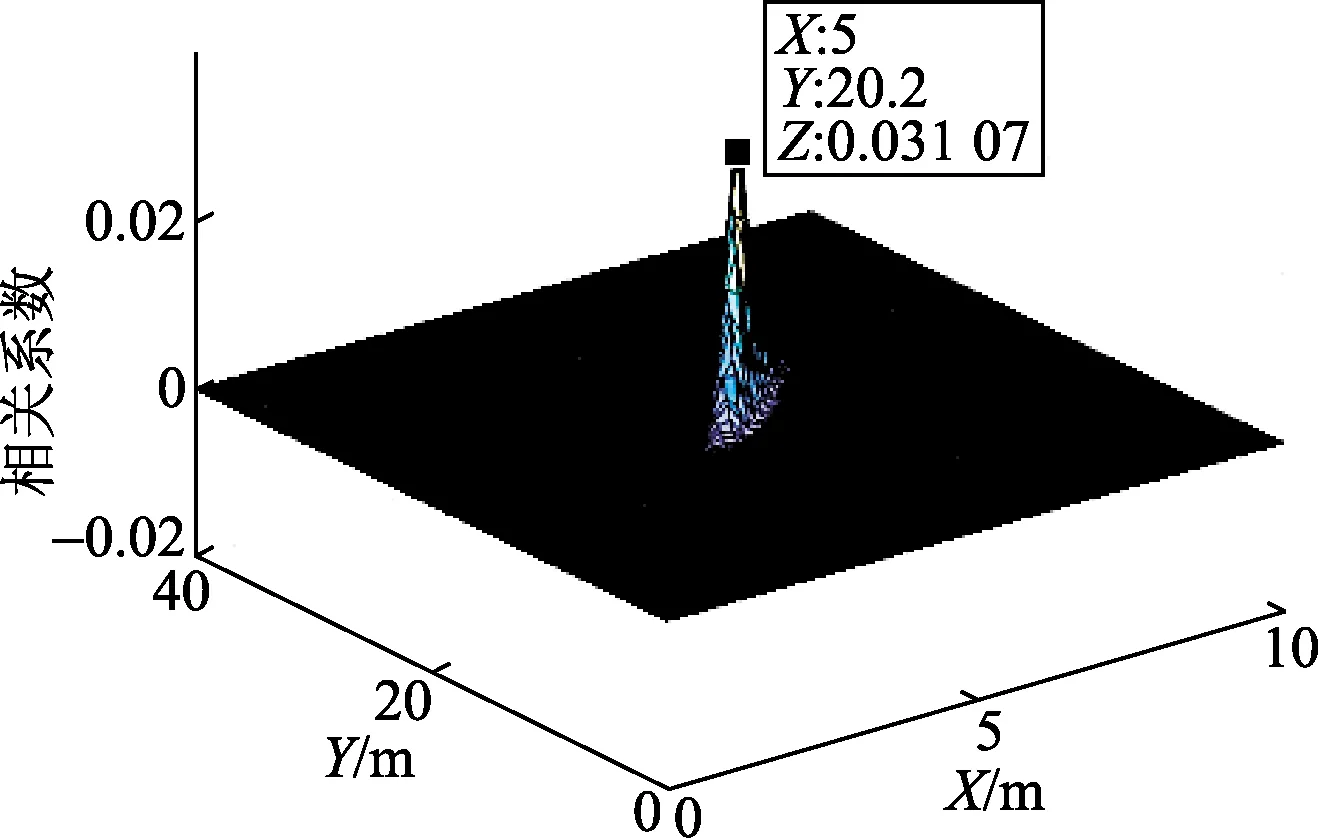
图8 八元直线阵列定位实验结果

在相同实验环境下，重复进行上述实验，然后分别提取阵列01100110、10100101、10101010、11000011、11001100相对应传感器的输出数据，得到声源定位结果如表1所示。选取定位实验结果与计算均值相一致的数据，绘制阵列声源定位图如图9所示。

通过仿真与试验的研究可以得到以下结果。

(1)定位实验中只有01100110与10101010这两种四元阵列定位误差小于1%，其结构示意图如图10所示。

(2)由于仿真的时候噪声设置为白噪声，并不能完全模拟真实噪声，因此，在实验的仿真得到5个四元拓扑结构，但经过实验检验后只有2个满足要求。

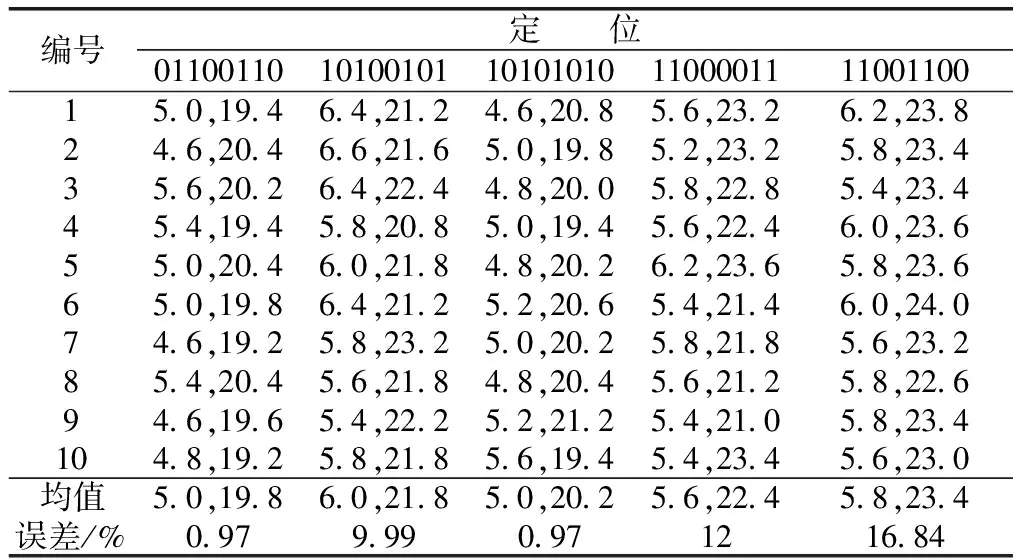
表1 实验结果

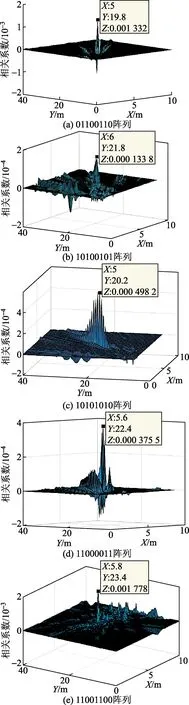
图9 最优阵列实验定位结果

图10 最优阵列结构示意图

(3)扫描步长为0.2 m，所以误差皆为0.2的倍数，可以通过减小扫描步长来进一步提高定位精度。

(4)下一步将进行定位误差分析，寻找影响定位的各个误差源，分析误差服从的分布规律，得出定位的测量不确定度。

4 结论

为消除声源定位直线阵列中的冗余阵元，精简阵列结构而不影响定位精度，开展了基于HBT干涉定位的直线阵列优化研究。基于HBT干涉定位原理建立仿真定位模型，对阵列进行编码优化仿真，得到声学定位性能最优的5个直线传感阵列。并通过定位实验对所得四元优化阵列进行验证，结果表明有2个四元直线阵列的定位结果在设定误差范围内，基本达到与八元直线阵列一致的定位性能。研究结果将有效减小定位系统体积、优化阵列结构和提高定位效率。