基于电容式微机械声学传感的纳米梁非线性振动控制

万 磊, 刘灿昌, 孔维旭, 黎德祥, 周英超

(山东理工大学交通与车辆工程学院，淄博 255049)

随着纳机电系统(nano-electromechanical systems，NEMS)研究的快速发展，纳机电系统的振动控制越来越引起相关研究人员的注意。纳米梁在振动时容易产生多值等非线性现象，影响纳机电系统的工作稳定性。因此，纳米梁的非线性振动控制成为纳机电系统的一个重要研究方向[1]。

目前针对电容式微机械声学传感器(capacitive micro-mechanical acoustic sensors，CMUT)的研究也越来越多。张睿等[2]开展了对CMUT动态性能的仿真与测试。Mukhiya等[3]通过实验验证了在挤压膜阻尼现象下具有频移的单个六边形单元的特性。Sangjun等[4]研究了具有低偏置电压的CMUT有作为便携式化学传感器系统关键部件的潜力。Khan等[5]提出一种机载塌陷电容微机械超声换能器作为一种实用的超声换能器。张丹丹[6]研究了一种可以有效处理超声波信号的CMUT样品。卓文军等[7]对电容式机械超声阵列尺寸进行了优化。张慧等[8]对电容式微超声换能器阵列进行了一系列实验研究。Engholm等[9]介绍了两个换能器阵列探头的特性。

近年来，对于纳机电系统的非线性振动分析与控制研究取得较大的进展。Liu等[10]研究得到了纳米梁谐波激励主共振的最优控制。杨晓东等[11]分析了基于非局部效应两端铰支纳米梁的横向非线性振动。Khaniki等[12]分析了嵌入变化非线性弹性环境中的纳米梁。Bornassi等[13]建立了纳米器件在静电力和分子间力作用下的运动方程并进行求解。Beni等[14]对梁式纳机电系统的静态不稳定性进行了理论研究。Ebrahimi等[15]提出了非经典梁的模型，用于纳米梁在弹性地基中的非线性振动分析。巩庆梅等[16-17]研究了纳米梁非线性振动电容式传感器控制方法。Zhao等[18]研究了残余表面应力对悬臂纳米梁非线性动力学行为的影响。Najar等[19]研究了在非线性力和直流电压作用下纳米梁的动态响应。

纳机电系统存在的问题是NEMS器件处于纳米尺寸，普通的振动信号传感器尺寸接近甚至大于纳米梁和控制器件的尺寸，无法应用到纳米梁振动信号检测中，所以振动信号的传感成为纳米梁振动控制的难题[1]。研究一种新型的基于电容式微机械声学传感的纳米梁非线性振动控制方式，以期解决振动信号检测难的问题。

基于电容式微机械声学传感的纳米梁非线性振动控制，将CMUT器件置于纳米梁下方作为振动信号检测传感器。以Euler-Bernoulli梁为振动模型，应用多尺度方法研究纳米梁的非线性振动控制。仿真出幅频响应曲线图，分析纳米梁的振动非线性，研究改变系统参数来减弱系统非线性的方法。希望通过选择合适的系统参数可以减弱甚至消除系统振动的非线性，增强系统的稳定性。

利用了CMUT器件体积小、灵敏度高的优点，将其作为振动信号传感器应用于纳米梁振动信号的检测中，以进行纳米梁非线性振动控制研究。

1 电容式微机械声学传感器原理

如图1所示，电容式微机械声学传感器器件主要由石墨烯薄膜和电极构成，在其接收模式下，声波激励薄膜使薄膜产生形变位移，从而导致薄膜与对应的下面电极板之间的电容值发生改变。对薄膜位移的响应，电容式微机械声学传感器的输出电流i可以表示为[20]

(1)

式(1)中：ωa为声波的角频率；C为CMUT器件的电容；Vb为直流偏置电压；Δx为薄膜位移；d0为导电薄膜与背部电极的距离;d为纳米梁和上下极板间的初始距离;k为比例系数；w为纳米梁的挠度。

图1 电容式微机械声学传感器示意图

2 基于电容信号传感的纳米梁静电激励振动控制模型

图2 纳米梁振动模型

作用于纳米梁与静电驱动极板间的激励电压V为

V=VD+Va=VD+V0cos(ωt)

(2)

式(2)中：Va=V0cos(ωt)为交流激励电压。

为便于分析，引入无量纲量:

(3)

式(3)中：u为纳米梁振动时的无量纲位移；x*为X方向上的坐标；x为X方向上的无量纲坐标；l为纳米梁的长度；t*为时间；t为无量纲时间；E为纳米梁的杨氏模量；I为截面惯性矩；ρ为纳米梁的密度；A为纳米梁的横截面积。

作用于纳米梁与控制极板间的控制电压VC为

(4)

式(4)中：g为控制增益。

在静电控制力作用下，基于电容信号传感的纳米梁非线性振动微分方程可表示为

(5)

经过无量纲处理后纳米梁的动力学方程可变为

(6)

式(6)两边同乘(1-u)2(1+u)2得到：

(7)

ε[VD+V0cos(ωt)]2(n7x2+n8x+n9)

(8)

应用多尺度法将式(8)的近似解用以下形式表示[21]：

x(t,ε)=x0(T0,T1,T2)+εx1(T0,T1,T2)+

εx2(T0,T1,T2)+…

(9)

式(9)中：ε是无量纲参数；T0=t，表示快变时间尺度；T1=εt，表示慢变时间尺度。

取纳米梁外激励频率近似等于纳米梁的固有频率，得到激励频率为

ω=ωn+εσ

(10)

式(10)中：σ为激励频率调谐参数。

将式(9)与其对时间的导数代入式(8)，再将式(8)“=”两边ε同次幂的系数相等，得到：

(11)

μn2x0D0x0+μn3D0x0+

[VD+V0cos(ωt)]2×

(12)

将式(11)的近似解表示为

(13)

(14)

处理过程中利用以下变换:

(15)

将式(13)、式(15)代入式(12)，为避免出现久期项，得到：

n7VDV0A2e-jσT1=0

(16)

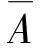
D1a=m1a3+m2a+(m3a2+m4)sinφ

(17)

aD1φ=σa-m5a3+m6a+(3m3a2+m4)cosφ

(18)

(19)

(20)

求得系统主共振的幅频响应方程和相频响应方程为

(21)

(22)

只考虑非线性项的影响，得到无量纲动力学方程对应的Hamilton方程为

(23)

为便于分析，假定原点(x,y)=(0,0)处该保守系统的势能为0，由此得到系统的势能函数V(x)及Hamilton函数H(x,y)如下:

κx-(2κ-η)ln(x+1)+2γ-η+κ+

(2κ-η)ln1

(24)

(2κ-η)ln(x+1)+2γ-η+κ+

(2κ-η)ln1

(25)

3 数值模拟及分析

以Euler-Bernoulli梁一阶振动模态为例进行分析，纳米梁的参数值如表1所示，进行仿真之后得到系统振动的幅频响应曲线图、非线性项变化图以及势能曲线图。

表1 纳米梁参数值

如图3所示为控制增益g不同时的幅频响应a曲线。在所选取参数范围内以及其他参数保持不变时，改变控制增益的大小会对纳米梁的振动非线性产生影响。当g=10.80时，在共振频率点左侧出现系统振动不稳定的非线性区间。当g从10.40变为10.02时，系统的最大振幅减小且系统振动非线性减弱，逐渐趋于稳定。由此可得控制增益的取值在选取范围内时，控制增益减小，系统振动非线性减弱。

图3 控制增益不同时的幅频响应曲线

如图4所示为系统阻尼μ不同时的幅频响应曲线。在所选取参数范围内及其他参数保持不变时，改变系统的阻尼对纳米梁振动的振幅和振动非线性同时产生影响。当μ=0.7×10-2时，在共振频率点左侧出现系统振动不稳定的非线性区间。当μ从1.4×10-2变为2.1×10-2时，系统的最大振幅减小且系统振动非线性减弱，逐渐趋于稳定。由此可得系统阻尼的取值在选取范围内时，系统阻尼越大，系统振动的振幅越小，振动非线性越弱。

图4 系统阻尼不同时的幅频响应曲线

如图5所示为直流激励电压不同时，非线性项随控制增益变化曲线。将非线性项控制在合理范围内有助于提高系统振动的稳定性。在所选取参数范围内以及其他参数保持不变的情况下，当直流激励电压一定时，非线性项随控制增益的增加呈现出先增加后减小的趋势。当控制增益一定时，直流激励电压越大，非线性项越小。

如图6所示为交流激励电压不同时的幅频响应曲线。在所选取参数范围内以及其他参数保持不变时，改变交流激励电压会对纳米梁振动的振幅和振动非线性同时产生影响。当V0=0.85 V时，在共振频率点左侧出现系统振动不稳定的非线性区间。当V0从0.50 V变为0.15 V时，系统的最大振幅减小且系统振动非线性减弱。由此可得交流激励电压的取值在选取范围内时，交流激励电压越小，系统振动的振幅越小，振动非线性越弱。

图5 直流激励电压不同时非线性项随控制增益变化曲线

图6 交流激励电压不同时的幅频响应曲线

如图7所示为直流激励电压不同时的幅频响应曲线。在所选取参数范围内以及其他参数保持不变时，改变直流激励电压会对纳米梁振动的振幅和振动非线性同时产生影响。当VD=9.0 V时，在共振频率点左侧出现系统振动不稳定的非线性区间。当VD从9.6 V变为10.0 V时，系统的最大振幅变化不大但是系统振动的非线性减弱。由此可得直流激励电压的取值在选取范围内时，直流激励电压越大，系统振动的非线性越弱。

图7 直流激励电压不同时的幅频响应曲线

如图8所示为势能[V(x)]曲线随参数γ的变化，可以看出，物理意义上的平衡点存在3个。在原点左侧，势能随着γ的增大逐渐增大，在原点右侧，势能随着γ的增大逐渐减小。

图8 势能曲线随参数γ的变化

4 结论

(1)系统的阻尼、控制增益、直流激励电压和交流激励电压都是影响系统振动的因素，其中，改变系统阻尼和交流激励电压对系统振幅产生较大的影响，控制增益和直流激励电压对振幅影响较小。在所选取的参数范围内，适当增大系统的阻尼和减小交流激励电压都可以减小系统的振幅。

(2)改变其中任何一个参数均对系统振动的非线性产生影响，选取合适的系统参数可以有效地对系统非线性振动进行控制与调节，提高系统的稳定性。

(3)分析幅频响应曲线可得，通过增大系统阻尼、减小控制增益、增大直流激励电压以及减小交流激励电压可以减弱系统振动的非线性。