基于RDK-ELM的航空发动机控制系统故障诊断

陈虹潞，黄向华

（南京航空航天大学能源与动力学院，南京210016）

0 引言

现代航空发动机数字控制系统主要由传感器、执行机构及电子控制器等组成[1]，其中，传感器和执行机构组件繁杂，容易发生故障，是控制系统中十分重要又脆弱的环节，因此必须对传感器和执行机构进行实时故障诊断，从而采取必要的容错控制措施以保障发动机工作性能不受影响。

故障诊断方法主要有3种：基于模型的、基于人工智能的和基于数据驱动的方法。基于模型的故障诊断方法从1977年被Spang等[2]提出，目前已较为成熟。在NASA和MTU合作进行的关于先进智能发动机传感器和执行器性能要求的研究中所提出的未来智能发动机发展的可行技术中，就包括用于提高发动机的气路部件性能和延长发动机的在役寿命的通过基于模型的控制和监控技术[3]。基于模型的方法应用发动机部件级模型作为机载模型，通过扩展卡尔曼滤波器（Extended Kalman Filter，EKF）自适应跟踪发动机感测信号的输出，在发动机发生故障时，EKF的信号估计值偏离发动机实际信号值产生残差，通过计算对残差进行分析即可诊断发动机的故障类型[4]。

近年来人工智能算法兴起，不少学者将BP神经网络、径向基网络、自联想网络、支持向量机等算法应用于故障诊断中[5-8]，其中基于梯度训练的神经网络算法泛化能力较差，易陷入局部最优；而支持向量机参数选择复杂，训练速度慢，不适于故障诊断的工程应用。Huang等[9]提出的极限学习机（Extreme Learning Machine，ELM）算法是1种新型前向神经网络算法，无需迭代，学习速度快、精度高且易于调参；随着核函数的引入，ELM获得了更高精度[10]。Wong等[11]提出具有深度学习网络结构的多层核极限学习机（Multilayer Kernel Extreme Learning Machine，ML-KELM）；逄珊等[12]将其应用于航空发动机的气路部件故障诊断中，获得了更优的诊断精度。但深度学习结构通过多层网络逐层进行输入数据的特征提取，计算耗时严重，对需要高实时性的发动机故障诊断来说是不容忽视的缺陷。

针对深度核极限学习机的训练时间过长的不足，本文将Deng等[13]提出的核极限学习机的简约方法与深度学习网络结构结合，提出简约的深度核极限学习机（Reduced Deep Kernel Extreme Learning Machine，RDK-ELM）。该算法利用随机支持向量缩短算法训练时间，并保留深度学习网络结构的高精度优点，对EKF产生的残差数据进行模式识别分类，实现航空发动机控制系统传感器与执行器的故障诊断。

1 多层核极限学习机的推导

1.1 极限学习机

极限学习机是Huang等提出的1种新的单隐层前向神经网络的快速学习方法。在ELM算法中，给定训练样本：{(xi,ti)∈Rd,ti∈R，其中，N 为样本数量，d为维数，m为输出节点数，对于如本文所述的故障诊断分类问题，m为类别数。单隐层前向神经网络的ELM输出函数为

式中：L 为隐藏节点的数目；β=[βi，…，βL]T，为输出权重向量；h(·)为激活函数；ai为隐藏节点的权重；bi为隐藏节点的偏差。

式（1）写成矩阵形式为

输出权值β可通过寻找给定系统的最小二乘解获得，即求解式（2）的最小范数的最小二乘解为

式中：C为正则化系数。

1.2 核极限学习机

如果激活函数h(·)是1个隐函数，则可以对ELM算法应用Mercer条件，并引入核矩阵[10]

即对任意每2个训练样本之间求核函数

将式（6）、（7）与式（5）代入式（1）中，可以得到核形式的输出函数

这样就得到了核极限学习机KELM。

1.3 多层核极限学习机

多层核极限学习机ML-KELM是将核方法引入到多层极限学习机的1种算法。多层极限学习机[14]（Multilayer Extreme Learning Machine，ML-ELM）与深度置信网络（Deep Belief Net-work，DBN）相似，DBN是由多个受限玻尔兹曼机[15]（Restricted Boltzmann Machaine，RBM）叠加而成，逐层提取特征获得更抽象的概念。ML-ELM由多个极限学习机自编码器（ELM Auto-Encoder，ELM-AE）叠加而成，但相比于 DBN，ML-ELM不需要对网络权值进行整体微调，且无需迭代，因此训练速度较DBN有显著提高。

ML-KELM由多个核极限学习机自编码器（Kernel Extreme Learning Machine Auto-Encoder，KELM-AE）构成，KELM-AE 的结构如图1所示。

文献[11]中给出了ML-KELM的详细推导过程。类似于式（7）的核函数映射计算，KELM-AE的输入矩阵x(i)通过核函数κ(i)(xk,xj)被映射为核矩阵Ω(i)，核函数可以选用RBF核函数中，σi为核参数。计算得到核矩阵后，输入向量的特征提取可以表示为

式中：g(·)为激活函数，与式（1）中的 h(·)都是激活函数，可从多种激活函数类型中根据实际情况与实际问题自定义选取，在不同的算法中可以不相同。

在ML-KELM的训练过程中，输入数据由多层KELM-AE逐层进行特征提取，每层的和X(i)都可由式（11）、（12）计算得到。最终得到的数据特征Xfinal作为1个KELM分类器的输入来计算最终的分类结果，KELM分类器的模型为

式中：Ωfinal为由Xfinal计算得到的核矩阵，则βfinal为

2 简约深度核极限学习机的推导

2.1 简约核极限学习机

简约核极限学习机（Reduced Kernel Extreme Learning Machine，RKELM）是在KELM的基础上，从输入样本中随机选择部分样本作为支持向量进行计算，在保持较高精度的同时大幅提高了训练速度。

对给定的N个训练样本ℵ={(xi,ti)∈Rd,ti∈，给定支持向量数目S，则支持向量XS={xi|xi∈为

式中：ΩN×S=K（X，XS），为简约的核矩阵。

式（9）在求取核矩阵时，是对每个输入向量都进行核函数计算，而此处简约的核矩阵仅对S个支持向量进行核函数计算，计算量大大简化。β=[β1，β2，…，βS]是输出权重矩阵

2.2 简约深度核极限学习机

在ML-KELM的计算中，每层KELM-AE的特征提取都是对全部输入数据计算核矩阵，虽然可以保证高精度，但付出了高耗时的代价。对此，本文提出简约的深度核极限学习机（Reduced Deep Kernel Learning Machine，RDK-ELM），每层特征提取由RKELM-AE完成。对于第i层RKELM-AE，编码器从输入数据X(i)中随机选择 L(i)个支持向量，根据式（16）、（17）计算变换矩阵，逐层完成特征提取，最后通过1个RKELM分类器计算出分类结果。RKELM-AE算法的计算过程见表1，RDK-ELM算法的计算过程见表2。

表1 RKELM-AE算法的计算过程

表2 RDK-ELM算法的计算过程

相比于ML-KELM算法，RDK-ELM算法中每层RKELM-AE都选择部分样本作为支持向量，当支持向量为全部样本时，RDK-ELM算法与ML-KELM算法等效[13]。所以通过合理选择各层支持向量的数量，可以得到训练时间短、分类精度高的RDK-ELM算法。

3 算法在通用分类数据上的比较验证

为验证本文提出的RDK-ELM算法在速度与精度上的性能，首先将其与基本ELM、KELM、RKELM以及基于深度学习结构的ML-KELM算法在4个典型UCI分类数据集上进行综合比较。4个UCI数据集样本的相关参数见表3。

表3 UCI分类数据集的数据

研究采用的计算机配置为：Core i5-8250U，内存8G。算法验证的软件平台为：Matlab R2016b。

算法参数设置：所有算法的激活函数均设置为Sigmoid函数，核函数均设置为RBF核函数。试验验证发现，ML-KELM和RDK-ELM算法均在隐含层为2层时精度最好，故层数均设置为3。正则化因子C和核参数σ的取值在10-7～107范围内经过试验选取最优设置。具体每种算法的正则化因子、核参数、支持向量数的设置见表4～8。

表4 ELM算法的隐含节点数设置

表5 KELM算法的参数设置

表6 RKELM算法的参数设置

表7 ML-KELM算法的参数设置

表8 RDK-ELM算法的参数设置

5种算法在4个UCI分类数据集上的性能结果见表9～11。由于ELM算法需要随机生成权重与偏差，RKELM和RDK-ELM算法需要随机选择支持向量，其运算结果具有不确定性，因此这3种算法的性能参数是取100次运算的平均值，KELM和ML-KELM则是1次的运算结果。表中，Tr.time为Training time的缩写，表示训练时间，s；Ts.rate为Testing rate的缩写，表示测试分类正确率。

表9 ELM与KELM的训练时间与分类正确率

表10 RKELM与ML-KELM的训练时间与分类正确率

表11 RDK-ELM的训练时间与分类正确率

从表中可见，ML-KELM算法的分类正确率在全部数据集中都是最高的，说明基于深度学习网络结构的KELM算法具有较好的泛化性能和分类能力。本文所提出的RDK-ELM算法的正确率与KELM算法的差距非常小，且样本数据越大，差距越小，可以说二者的分类能力几乎持平。

但从训练速度方面而言，RDK-ELM算法的训练速度明显比KELM算法的更快。在5种算法中RKELM算法的训练速度最快，但精度不如RDK-ELM算法的；而ML-KELM虽然精度非常高，训练速度却最慢，对工程应用来说是不可回避的缺陷。

RDK-ELM算法通过深度学习网络结构，在RKELM算法的基础上获得了更好的泛化性能与分类能力，同时比KELM和ML-KELM算法具有更快的训练速度。在这4个UCI分类数据集上的试验表明，本文提出的RDK-ELM算法是同时具有较好的精度与速度的算法，可用于航空发动机控制系统中的传感器与执行器的故障诊断。

4 算法在涡扇发动机故障诊断中的验证

为验证RDK-ELM算法在航空发动机控制系统故障诊断中的性能，本文以某型涡扇发动机为研究对象，采集数据样本进行故障诊断仿真试验。

4.1 故障模式和故障数据样本

实际的航空发动机传感器与执行器的故障数据是非常难获得的。为了进行故障诊断的仿真试验，采用文献[16]中的方法，利用某型涡扇发动机部件级模型模拟发动机的故障，通过自适应机载模型产生EKF残差，采集故障状态下的EKF残差数据，作为训练样本和测试样本数据集。

本文主要研究发动机传感器和执行器的故障诊断，但实际情况中也可能发生气路部件的故障，为验证算法区分控制系统故障与气路部件故障的能力，选取高压压气机（High Pressure Compressor，HPC）和高压涡轮（High Pressure Turbine，HPT）2个气路部件的故障进行研究。选取的传感器有：低压转子转速传感器（Nl），高压转子转速传感器（Nh），高压压气机出口压力传感器（P3）；选取的执行器为主燃油阀Wf。研究假设传感器与执行器最多只有2个同时发生故障，则有12种故障模式，6种单故障研究样本见表12，6种双故障研究样本见表13。表中“F”表示该部件发生故障，“-”表示无故障。

对于实际应用于发动机的故障诊断算法来说，发动机的飞行高度、马赫数及其工作状态会影响发动机感测信号的值，是非常重要的影响因素。但研究表明，发动机的状态对于故障诊断算法的可行性研究影响不大，在额定和最大工作状态下，由算法得到的性能结果相同[16]，因此本文仅选择在发动机高度H=0，飞行马赫数Ma=0，最大工作状态下进行数字仿真试验验证算法的可行性。

表12 单故障研究样本

表13 双故障研究样本

发动机传感器、执行器、气路部件的故障程度根据文献 [4]所给定的数值注入发动机模型进行模拟。Nl、Nh传感器的故障偏置范围为-0.5%～-2.5%，P3传感器的故障偏置范围为-2%～-10%，Wf执行器的故障偏置范围为-1%～-8%，HPC和HPT的故障偏置范围为-1%～-5%。故障偏置数值通过随机数的方式在上述范围内产生，注入模型仿真来生成故障EKF残差数据样本。

为避免类不平衡的问题，对于表12中1～6的单故障情况，每种情况采集200个样本，对于表13中7～12的双故障情况，每种情况采集400个样本。则共有1200个单故障样本，2400个双故障样本，总计3600个样本。选取其中的80%作为训练样本，其余20%为测试样本。即训练样本数2880，测试样本数720。

由于9个EKF残差数据中有转速、压强、温度，各参数单位不一致且数量级相差较大，会影响算法进行故障诊断的精度，因此对EKF残差数据进行归一化处理

4.2 算法的故障诊断试验验证比较

为验证RDK-ELM算法在故障诊断中精度与速度的综合优势，将ELM、KELM、RKELM、ML-KELM和RDK-ELM算法应用于发动机控制系统故障仿真数据的诊断分类中进行比较分析。

算法参数设置：所有算法的激活函数均设置为Sigmoid函数，核函数均设置为RBF核函数。ML-KELM和RDK-ELM算法均在隐含层为2层时精度最好，故层数均设置为3。正则化因子C和核参数σ的取值在10-7×107范围内经过试验选取最优设置。ELM算法的隐含层节点设置为200；KELM算法的 σ=10，C=105；RKELM 算 法 σ=1，C=103，L=200；ML-KELM 算法 3 层核参数选择为 σ=[10，104，103]，正则化因子 C=[102，10-1，10]；RDK-ELM 算法 3 层核参 数 选 择 为 σ= [102，102，104]， 正 则 化 因 子 C=[10，1，104]， 支 持 向 量 L=[200，200，300]。 ELM、RKELM、RDK-ELM算法的运行结果是取100次运行结果的平均数，KELM和ML-KELM算法只运行1次。结果见表14。

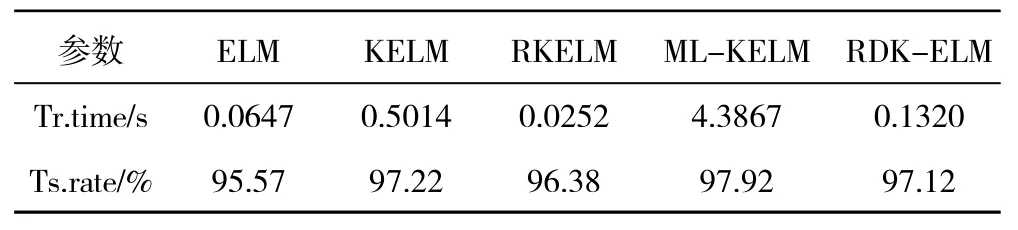
表14 各算法进行故障诊断的性能结果

从表中可见，ML-KELM算法精度最高，RKELM算法速度最快，RDK-ELM和KELM算法精度基本持平，但RDK-ELM比KELM算法的训练时间缩短了1/4。可见，利用深度学习结构结合核方法，可以提高算法的泛化性能与分类能力，在样本数量大、类别多的情况下精度更高；应用简约方法则明显改善了单纯核方法的时间性能。RDK-ELM算法将2种优点结合起来，得到优越的综合性能。

4.3 算法参数分析

RDK-ELM算法可以调整的参数有网络深度（隐含层层数）、每层核参数和正则化因子、每层支持向量数目。

（1）网络深度。虽然深度学习网络结构是通过逐层对输入数据提取特征来获得更高精度的，但本文对UCI分类数据集及发动机故障数据的试验表明，并不是层数越多精度越高，精度在隐含层层数为2时的精度最高，层数再高精度反而降低。此外，网络深度直接影响训练时长。因此将隐含层层数设置为2层具有最稳定的精度和可接受的速度。

（2）核参数和正则化因子。核参数σ和正则化因子C是在10-7～107范围内按10的倍数选取的，这2个参数对算法的精度有非常大的影响[11]。目前对机器学习算法的参数中，这2个参数的选取通常根据经验选择。通过试验调参，可以得到令人满意的精度。

（3）支持向量的数量。RDK-ELM算法选取的支持向量越多，精度越高，训练时间也越长。当支持向量为全部样本时，RDK-ELM与ML-KELM算法等效[13]。而在试验中，支持向量达到一定数目时，精度的提高就不明显了，而同时速度则明显降低。为了获得精度和速度的综合优势，支持向量的数目需要选取1个合适数值。在目前基于支持向量的算法的研究中，对支持向量数目的选取均没有理论上的方法，一般根据经验和试验选取。本文的算法是先取输入向量样本数目的1/10，然后以此为基准增加或减少支持向量的数目，以达到训练速度和训练精度的综合最优为止。

5 总结

（1）将RKELM算法与深度学习网络结构各自的优点结合，提出RDK-ELM算法。

（2）对UCI分类数据集和发动机故障仿真数据进行试验，验证了RDK-ELM算法在精度与速度上的综合优势。

（3）RDK-ELM算法可调参数较多，需要针对具体情形进行参数调整，通过试验验证以获得最佳性能。