走进思维内里，让数学学习深度发生

罗鸿斌

【摘 要】 促进理性思维发展，引导学生在数学学习与实践中习得思考方法，获得数学学习经验，发展和提升数学学习力和数学素养是数学教育的最终目标。因此，在数学教学中，教师应引导学生从数学表象走进思维内里，将数学教学活动从浅层次不断推向深入，在促进学生思维发展的同时，实现数学课堂深度学习的自然发生。

【关键词】 初中数学;思维内里;深度学习

促进理性思维发展，引导学生在数学学习与实践中习得思考方法，获得数学学习经验、发展和提升数学学习力和数学素养是数学教育的最终目标。因此，教师必须要改变当前数学浅层次教学现象，将教师从课堂中心转变出来，将数学课堂还给学生，唤醒学生主体意识，让学生的思维活跃起来，从而引领学生从表象走进思维内里，促进学生与教师、学生与数学知识之间的多元互动，让思维引发数学深度学习的发生。

一、利用旧知架设思维通道，扩展知识深度

数学知识存在密切的关系，呈现出螺旋式上升的规律。因此，在数学教学中，要将学生已学的知识和学生所要学习的新知识联系起来，使旧知识为新知识的学习提供支持，并促使新旧知识形成一个有机的整体，从而扩展学生知识深度，在知识之间建立起纵向、横向立体化知识网络。

例如《平面图形的认识（二）》的教学，从教材编排体系来看，编者就是将这部分的教学内容与《平面图形的认识（一）》关联起来。第一部分的内容涉及平面图形的基础知识，包括线、角、位置关系等。因此，在教学《平面图形的认识（二）》时，我先设计了知识回顾环节：（1）各画出线段、射线、直线;（2）画出一个三角形，标出余角、补角、对顶角;（3）画出一组平行线和垂直线。在此基础上，引出“探索直线平行的条件”学习内容。

这个环节的教学设计，改变传统口述的方式，用问题的方式引领学生动手操作，从而在实践中促使学生调动知识积累，并开动思维，从线、角、位置关系等三个方面进行系统建构，不仅自然地引出新知识，也促进学生动手能力和系统性思维发展，从平面图形的一般现象进入特殊现象，深入思考直线平行所需要具备的特殊条件，走进思维内里，引领学生系统、深度学习行为发生。

二、借助冲突制造思维困境，引发深度思考

在实施数学教学时，教师要善于利用学生的学习心理，从而根据学生的心理规律和特征，优化数学教学设计，引发学生深度思考。在数学教学中制造思维冲突正是利用学生数学学习心理，让学生经历思维挫折，从而让学生求知好奇心更加浓厚，引领学生走向数学学习的深处，拨开层层云雾，抵达思维内里。

例如《概率的简单应用》一章中“抽签方法合理吗”的教学，我设计了这样的情境：现在要从5名表现突出的同学中选出一名同学，参加艺术节表演活动，用白纸制作五个标签，一个标签上写有“参加”字样，其余四张没有写任何字符，然后将五张标签放在一个纸盒里，摇动10秒钟，让五名学生依次摸，摸到写有“参加”字样的同学参加艺术节表演。

在学生动手实践的基础上，我提出一个问题：有同学认为采用这种抽签的方式是不合理的，可是为什么在日常生活中，人们还要采用抽签的方法呢？请各小组根据教材内容，说明抽签方法到底合不合理。

学生通过抽丝剥茧，透过表面现象，进行深入的思考，尽管在抽签的过程中，每一位学生抽签的先后顺序存在不同，但是从每一个抽中签的可能性来分析，每一个人的可能性又是相同的。从这个意义来说，抽签又是相对公平的一种方式。通过这个环节的设计，利用看似存在认知冲突的学习场景，引起学生思维上的困惑，进而让学生的好奇心和求知欲活跃起来，将学生的思考推向深入。

三、利用思维导图显化思维，建立深度关联

思维是抽象的，这就导致学生思维训练存在很大的难度。要对学生进行有效的思维训练，这就需要教师能够调动数学教学智慧和教学经验，寻找学生思维训练的载体，从而借助思维载体引领学生思维成长，让思维借助载体显现出来，从而将数学课堂教学推向深入，将各个知识点有机关联起来，将碎片进行组合形成知识模块。

例如在教学“中心对称和中心对称图形”时，为了帮助学生理清轴对称和中心对称之间的关系，我们可以采用思维导图的形式进行显性的比较，轴对称图形至少具有一条对称轴，而中心对称，则存在一个对称中心。前者是沿对称轴对折，结果是重合，而后者则围绕中心旋转180度重合;最后再从平分角度进行比较。

借助思维导图，引导学生从三个方面对轴对称和中心对称进行比较，从而提高学生概念建构的系统性。不仅如此，三个方面又聚焦关键节点进行比较，让学生对轴对称和中心对称的本质特点获得清晰的认识，直接进入思维内里，改变传统数学浮于表面的现象。

四、重构思维拓展迁移场景，实现深度应用

搞清楚深度学习的关键落脚点是前提，也是走进思维内里的必要环节。目前，不少数学教师对数学课堂教学设计往往停留在知识传授方面，从而导致学生课堂听懂了，换一个场景学生又不懂了、不清楚了、不会运用了。这就需要我们基于深度学习的需要，重构思维拓展和迁移场景，构建新的数学运用场景，让学生进行迁移性学习，运用所学知识去解决新的问題。

例如二次函数的应用教学，我先设计了这样一道应用案例：有一个工厂，现在要存放一些材料，打算围出一个周长为45米的矩形场地，如果要让围成的矩形场地实用面积达到最大值，长和宽要取多少米？

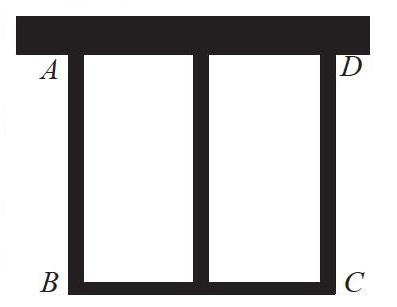
在讲解案例的基础上，我又重构新的应用场景：如右图，现在有一道长度为24米的篱笆，现在想要利用靠墙的一面（10米），围起来一个中间带有篱笆的长方形花圃，假设围成的花圃宽度AB是x米，面积是S平方米，能不能围成比45平方米更大的花圃？

这个环节，借助案例引导学生学会运用二次函数的知识解决实际问题，而新的应用场景的重构，基于案例又高于案例，进行了变式设计，不仅需要学生运用二次函数知识，而且需要学生思维参与，将二次函数的运用又推向深入。

总之，初中数学教学中，我们不仅要引导学生掌握基本的数学知识，还要激活学生思维，引导学生调动思维，从数学表象走进思维内里，将数学教学活动从浅层次不断推向深入，在促进学生思维发展的同时，实现数学课堂深度学习的自然发生。

【参考文献】

[1]周晓琳.浅议基于深度学习的数学课堂教学[J].初中数学教与学，2019（8）.

[2]周凌飞.基于思维深度参与的初中数学课堂教学实践研究[J].中国校外教育，2017（12）.