跨域云环境下基于动态异构网络的风险访问模型
文 静,袁家斌,王诗璇,魏利利
(1.南京航空航天大学计算机科学与技术学院,江苏 南京 211106;2.淮阴师范学院计算机科学与技术学院,江苏 淮安 223300; 3.中国兵器工业第二〇八研究所,北京 102202)
作为大数据的基础平台和支撑技术的云计算而言[1-2],云中的访问控制所涉及的资源可能由于云的分布式特点而位于不同域,这就构成了一个巨大而复杂的异构数据环境[3]。针对分布式异构环境下跨域安全互操作,要求能实现信息资源的安全共享[4]。当前在云端实现信息安全共享的主流方式是访问控制,访问控制主要有基于角色的访问控制、基于任务的访问控制和基于属性的访问控制3种[5]。在传统的分布式环境下,其访问控制模型中的主体一般只需一次授权即可使用,对环境的动态变化适应性较差。但是在云环境下,异构网络具有动态变化的特性,节点或边的变化会对当前的风险识别及跨域访问造成影响[6-7]。不确定性和动态性是多自治域环境的特点,保证数据资源安全性是安全策略的基本要求,二者之间的矛盾给多自治域环境中互操作带来许多风险和安全隐患[8-9]。目前针对动态异构网络中的访问控制机制未能较好地利用历史访问信息,限制高风险的节点访问,也没有对风险值进行实时更新,自适应性较弱[10]。
Lyu等[11]提出了一个云服务下基于图形工具的安全风险评估模型,可以清晰描述云服务的虚拟化安全风险场景,准确评估虚拟化安全风险因素,其方法能够较好地模拟云服务中复杂的动态安全问题。Zheng等[12]针对云模型不适用于非正态分布的问题,提出了一种基于均匀分布的一维后向云算法,建立了一种可信度评估指标,并将其应用于云中可信度评估,然而该算法仅适用于单个云环境的情况。Uikey等[13]提出了一种可扩展的访问控制体系结构和授权机制,该机制为多领域云环境下的资源管理策略提供了一个灵活的框架,但是该方法没有考虑到风险的因素。Dos-Santos等[14]针对传统访问控制模型无法满足特定安全要求的问题,提出了一种基于XACML扩展的风险管理框架,然而该框架没有考虑到访问双方的历史信息。Laleh等[15]提出了一种针对用户行为的风险评估模型,认为如果用户行为与“正常行为”的差异越大则风险越大,然而在云环境中,定义完整的“正常行为”几乎是不可能的。从已有的文献来看,较少考虑到访问记录对于风险的影响,无法适应异构跨域访问。拒绝频繁访问的操作没有考虑允许低风险高优先级的主体访问请求。
本文针对大数据云平台分布式异构环境下节点跨域访问风险问题,考虑到多个安全管理域的特点,建立跨域的访问控制模型,将自适应的风险动态阈值运用于带有记忆分量的多级安全模型中,对发起访问的主体和被访问的客体进行风险预审核,在本次访问请求结束后,无论访问是成功还是失败,管理节点都会实时调整本域风险阈值,使之具有一定的动态适应性,从而提高访问的灵活性,降低访问的风险,保证系统的安全性。
1 风险访问模型
分布式环境下的节点具有较强的动态性和不确定性,节点的风险值会随着访问历史记录及时间的变化而改变。本文的风险量化采用定量和定性相结合,随着历史访问次数的增加,风险值会变得越来越客观。模型涉及的风险值主要包含节点的风险值和域风险值。节点风险值由初始风险值、历史风险值和频率风险值组成。域风险值由本域指定的管理节点保存。当本域节点产生变化时需要对域风险值进行实时调整和更新。域中节点的风险值表示为ri(i=1,2,…,m),m为域d中的节点总数。
1.1 模型概述
云中任意自治域中的主体向域中客体发出访问请求。首先,由管理节点主观设置风险阈值初始值赋予所属域管理节点。访问过程中需要将主体在访问周期内访问次数计数器的值和设定的最大访问次数进行比较,如果该值小于设定的最大访问次数则可以进入下一步;否则该节点将被定义为频繁访问节点,需要判断节点是否为低风险节点。如果该节点为低风险节点,则由本域管理节点分配预支风险值进入下一步。当该节点的风险值小于访问域和被访问域设定的风险阈值,被访问域中的客体才会对主体的访问请求做出反馈。当访问请求结束后,不管本次访问请求成功与否,访问发起域和被访问域的域管理节点都需要对本次访问操作相互做出评价,各域管理节点根据评价值修改本域风险阈值。
1.2 初始风险值
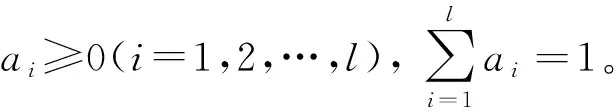
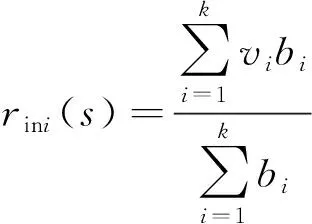
(1)
式中:bi——评价结果向量B中第i个评价结果。
1.3 历史风险值
历史访问记录是评估节点风险的重要信息,对节点间交互的历史访问记录进行综合与分析,得出每一个节点的历史风险值。可以将历史风险值rhis分为两部分,即直接访问风险值rhis1和间接访问风险值rhis2。
1.3.1 直接访问风险值rhis1
rhis1表示历史直接访问累计的风险值。Hij表示主体si申请访问客体oj的总次数,Sij表示节点间直接交互过程中成功的次数,Fij表示节点间直接交互过程中失败的交易次数,无法确定交互是否成功或者失败的次数用Uij来表示,显然Hij=Sij+Fij+Uij。直接访问风险值可表示如下:
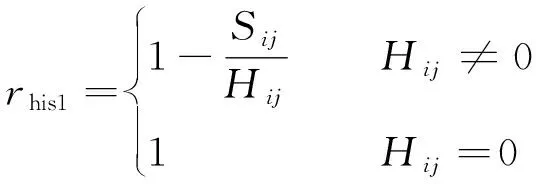
(2)
在访问周期内,为使直接风险值更加客观,设定t为风险更新的时间片,很明显t (3) 式中:ΔSij——本访问周期交互成功的次数;μ——由本域管理节点设置的更新权重,如果ΔSij大于本访问周期交互失败的次数,则约定μ∈(0.5,1),否则μ∈(0,0.5)。 1.3.2 间接访问风险值rhis2 被询问节点k必须和询问节点i有过安全的历史交易,节点可信,可以表示为如下形式:Pij={k|Sik+Fik>0,rhis1(Jreqi,k)>0}(Jreqi,k表示主体节点i对客体节点k历史访问的函数),则间接访问风险函数可表示为 (4) rfre=1-e-fij (5) 预支风险值是系统在每个访问周期为低风险节点预支的风险额度值,代表系统对其造成风险的容忍程度,也表示系统对低风险节点的信任。在本模型中,如果访问周期td-p内主体节点发起访问的次数已经超过cmax(cmax为域节点根据本域情况自主设定的周期内最大访问次数),并且节点在本周期内访问记录良好(即为低风险节点),且在本访问周期内访问优先级较高,那么可以向管理节点额外发出继续访问的申请,管理节点会在本周期内通过预支一定额度风险值的方式允许低风险节点的访问申请,以此提高整体访问的效率。 管理节点根据申请节点的历史访问信息为其分配风险机动额度φsi,此额度会随着访问的增加而减少,φsi=φsi-rsi。参考历史访问记录,在周期td-p内,对于每一次访问(Jreqi(si,oj,x)(j=1,2,…,n),根据直接访问风险值,基于信息熵的计算公式,得出si在oj下的信息量为 (6) 式中:csi——访问次数计数器的值。 定义1C为各风险分量权值的集合,C=(α,β1,β2,γ),其中α+β1+β2+γ=1,它们分别表示初始风险值、直接访问风险值、间接访问风险值和频率风险值的权值。节点综合访问风险值的计算式为 r=[α,β1,β2,γ][rini,rhis1,rhis2,rfre]T+φsi (7) 域整体风险值rd,可以通过域中所有节点风险值求平均值得到: (8) 本模型是一个状态机模型,系统的状态是系统中元素的表示,它由主体、客体、访问属性、访问矩阵以及标识主体和客体的访问类属性的函数等组成。其相关定义如下: 定义2S={s1,s2,…,sm}表示主体的集合。O={o1,o2,…,on}表示客体的集合。 定义3D={d1,d2,…,dp}表示多自治域构成的域集合。 定义4函数dom():S∪O→D,表示主体或客体所在的域。每个主体或客体都有唯一所在的域。 定义5集合A={rd,a,w,e}表示访问属性集,定义模型有以下4种访问方式:(a)Read(rd)读包含在客体中的信息;(b)Append(a)向客体中添加信息,且不允许读客体中的信息;(c)Write(w)向客体中写信息,且允许读客体中的信息;(d)Execute(e)执行另一个客体(程序)。 定义6当前访问集合B⊆(S×O×A):表示在某个特定的状态下哪些主体以何种访问属性访问哪些客体。 定义7访问请求集合JREQ,函数Jreq(si,oj,x)表示主体si对客体oj的访问,其中x∈A。 定义8访问矩阵集M,表示系统中所有主体对系统中所有客体所拥有的访问权限,元素Mij⊆A表示主体si对客体oj具有的访问权限。 定义9模型中节点状态集表示为V={V0,V1,V2,…,Vk},状态v∈V,由(b,M,f,sM,R)表示,其中b∈B,f为访问周期内的访问频率,sM∈S,R为风险函数集合,表示主客体的风险状态。用v*表示通过请求之后的状态。 定义10安全标记函数集合F,主体、客体的当前安全标记用访问类函数f表示,f=(fSH,fSL,fIH,fIL,fSO,fIO),f∈F,其中fSH、fSL和fSO分别表示主体和客体的保密级区间和函数,fIH、fIL和fIO分别表示主体和客体的完整级区间和函数。 约定1HIS(s)∈{hSH(s),hIL(s)}为主体的访问历史函数。 本文模型建立在经典的多级安全模型基础之上,是一个有限状态机模型,系统是安全状态,当且仅当系统的每一个状态(v0,v1,v2,…,vn)均为安全状态,其中v0是初始状态,v1,v2,…,vn是其他的输出状态。定义规则ρ:JREQ×V→G×V,表示给定一个请求和一个状态,规则ρ决定系统产生的响应和下一个状态。G为判定集{y,n,e,u},y表示请求被执行,n表示请求被拒绝,e表示多个规则适合于这一请求,u表示本规则不能处理此次请求。 定理2一个系统是机密性安全的,当且仅当它的每个状态都满足机密性强制规则。 公理1(简单安全性)状态v=(b,M,f,sM,R)满足简单安全特性,当且仅当所有的s∈S⟹[o∈b(s:r)⟹fSH(s)fSO(o)fSL(s)]。符号表示前者支配后者。 公理2(*安全特性)设s是S的一个子集,表示受*特性控制的主体。状态v=(b,M,f,sM,R)满足*特性,当且仅当所有的s∈S⟹[o∈b(s:a,w)⟹fSH(s)fSO(o)fSL(s)∧hSH(s)fSO(o)] 规则1′用于域d中主体si请求得到对域p中客体oj的read访问权。 ifJreq∉dom(Jreq(1)) thenJ’req(Jreq,v)=(u,v) else if [Jreq∈dom(Jreq(1))]∧[fSH(si)fSO(oj)fSL(si)]∧ [Jreqsi thenJ’req(Jreq,v)=(y,(b(∪(si,oj,r),M,f,sM,R))) elseJ’req(Jreq,v)=(n,v) Rd表示该域设置的风险阈值。 证明: a. 证明规则1′满足简单安全性公理。设ot∈(b′,r),若ot=oj,则fSH(si)fSO(oj)=fSO(ok)fSL(si),若ot≠oj则ot∈(b,r),由状态v=(b,M,f,sM,R)满足的先验条件知fSH(si)fSO(ot)fSL(si)。总之,若ot∈(b′,r)则fSH(si)fSO(ot)fSL(si),规则1′满足公理1。 b. 证明规则1′满足*特性公理。设ot∈(b′,a),若ot=oj,由规则1′可知,无论请求是否拒绝,都不改变模型中的append状态,则由ot∈(b,a),以及状态v=(b,M,f,sM,R)满足的先验条件知fSH(si)fSO(ot)fSL(si)∧hSH(si)≼fSO(ot)。 若ot≠oj,则ot∈(b,a),同上。 同理可证,ot∈(b′,w)时,fSH(si)fSO(ok)fSL(si)∧hSH(si)≼fSO(ot),总之,若ot∈(b′,a∨w),则fSH(si)fSO(ok)fSL(si)∧hSH(si)≼fSO(ot),则规则1′满足公理2。 其余规则可类似给出,此处省略。 公理3(简单完整性)满足简单完整性当且仅当客体的完整级在主体可访问的完整级区间,主体可读客体,即状态v=(b,M,f,sM,R)满足简单完整特性,当且仅当所有的s∈S⟹[o∈b(s:r)⟹fIH(s)fIO(o)fIL(s)]。 公理4(*完整特性)满足*完整特性当且仅当客体的完整级在主体的可访问完整级区间,且主体读过所有客体的完整级都支配主体要写客体的完整级时,主体可写该客体。状态v=(b,M,f,sM,R)满足简单完整特性,当且仅当所有的s∈S⟹[o∈b(s:a,w)⟹fIH(s)fIO(o)fIL(s)∧hIH(s)≼fIO(o)]。 证明: a. 证明其充分性。设Jreq是JREQ中的任意一个动作,T为系统的执行时间,对于(Jreq,v,p′,v′),当且仅当存在一个α=(v0,π1,v1,…)和某个t∈T,使得vt=(p,v),vt+1=(p′,v′)。 设v0=(b,M,f,sM,R)满足简单完整性,α=(v0,π1,v1,…)是一个执行,对每个t∈T,令vt=(bt,Mt,ft,sMt,Rt)。 证明v1满足简单完整性:设(Jreq1,v0,p1,v1)为一个变换,根据定理3中的(a)可得∀(s,o,x)∈(b1-b),满足简单完整性;令b∂={∀(s,o,x)∈b∧(s,o,x)}不满足简单完整性,根据定理3中的(b)可得b∂∧b1=∅。所以可得到∀(s,o,x)∈b1∩b0满足简单完整。并且由于∀(s,o,x)∈(b1∩b0∨b1-b0),得v1满足简单完整性。 证明若vt-1满足简单完整性,则vt满足简单完整性。 同理,可以证明vt-1和vt满足简单完整性。 综上所述,模型充分性得证。 b. 证明其必要性。采用反证法,假设模型满足简单完整性,则存在某个执行(Jreq,vt-1,pt,vt)使得下列条件其中之一成立:(a)某个(s,o,x)∈bt-bt-1不满足简单完整性;(b)某个不满足简单完整性的(s,o,x)∈bt-1∧(s,o,x)∈bt。 当(a)成立时,存在某个(s,o,x)∈bt-bt-1不满足简单完整性,所以vt不满足简单完整性,推得模型不满足简单完整性。当(b)成立时,由于存在某个不满足简单完整性的(s,o,x)∈bt-1∧(s,o,x)∈bt,所以vt不满足简单完整性,推得模型不满足简单完整性。 综上所述,必要性得证。 定理5一个系统是安全的,当且仅当它的每个状态都满足强制安全规则。 由于满足本模型机密性强制规则的系统是机密性安全的,同时满足完整性强制规则的系统是完整性安全的,由此可知定理5成立。 本文提出了分布式环境下的面向多域访问的动态多级安全模型,给出了定性和定量相结合的风险量化标准。在模型的访问域和被访问域增加了风险敏感标记的动态调整机制,每次访问之前需要通过本域管理节点的验证,提高了跨域访问的安全性,增加了模型的动态适应性。给出风险机动额度,结合历史访问信息,灵活地调整了主体访问能力,提高了访问控制模型的灵活性,实现了对风险的自适应访问控制动态授权,提高了模型对异构网络环境的适应能力。但是本模型在处理过程中没有充分考虑到在访问周期内如果有节点恶意篡改访问记录、伪造低风险或者无风险访问的假象。管理节点可以记录本域节点进域或者离域,并在访问前后对记录进行比较,或者对访问记录进行加密以防恶意篡改,这是下一步主要研究的工作。1.4 频率风险值
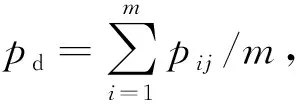
1.5 预支风险值
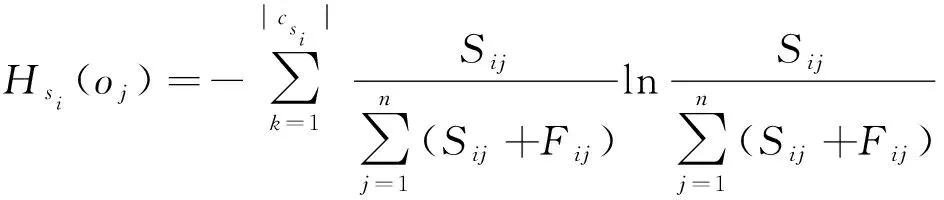
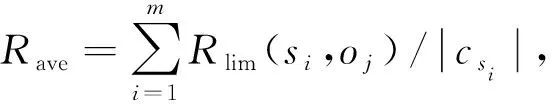
1.6 节点综合访问风险值
2 模 型 分 析
2.1 形式化描述
2.2 机密性分析
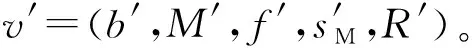

2.3 完整性分析
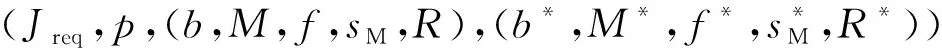
3 结 语

