面向生态友好的水库群调度模型
黄志鸿,董增川,周 涛,徐 伟,陈新颖,高晓琦
(河海大学水文水资源学院,江苏 南京 210098)
随着我国众多水利工程的修建,梯级水库群相继投入运行,使河流形成了碎片化现象,河流的生态分割日趋严重。主要表现为:河道断流,水生生物较少,渔业资源枯竭等[1]。虽经过治理有所好转,但恶化的态势没有得到根本遏制。而以往的水库调度在取得巨大的综合利用效益的同时,也使天然的河流径流情势和区域生态系统产生了变化。因此,改善水生态和水资源的合理利用是目前研究的两大需求[2],研究流域水库群生态调度,具有重要的意义。
近几年,在自然水文系统中考虑生态系统、面向生态友好的水资源管理等相关研究迅速发展,众多学者在考虑生态的目标决策及调度模型求解等领域有较为深入的研究[3-10]。目前水库调度对生态需水的考虑主要分为2种,一种是将生态需水作为一个特殊的用水户采取合适的权重加入目标函数中;另一种是将生态需水作为约束条件代入模型。将生态需水作为独立目标考虑的调度模型考虑了生活生产等社会用户的需求,但可能存在最优解不确定、不同用水户的需求满足与竞争不确定等问题[11]。而将生态需水作为约束,可以保证生态需水的优先满足,但这样的硬约束可能会导致调度结果难以被经济部门接受[12]。
传统对于生态目标的处理主要有生态缺水量最小或生态缺水率最小,这样的目标设置很可能在竞争中加大泄水量去寻得更小值,造成不必要的浪费。也有学者考虑寻大值,艾学山等[13]以下游河道的生态需水满足度最大作为生态目标去协调水库的发电、灌溉和生态环境效益,主要是对模型和算法的研究,而生态满足度达到100%之后的溢出情况没有做出分析。Yang等[14]以谢尔比维尔湖为例,生态上考虑最大化下游生态系统鱼类多样性建立了多目标优化模型,但未考虑社会和其他生态因素。Hu等[15]利用生物物理栖息地模拟方法(WUA法)进行生态效益评价,以平均生境面积最大作为生态目标的处理进行研究,是一种考虑物种和天然规律的方法,但是不同流量下该栖息地加权可用面积(WUA)是曲线变化的[16],并无详细解释以平均生境面积最大作为目标是否仍符合自然规律。
由于物种在演化过程中,逐渐适应了天然的时空变化规律,这就对生态径流的稳定性提出了较高要求。所以笔者认为,面向生态友好的调度中,应尽量使调度后偏离适宜生态需水区间的水量在可以接受的范围内,并且这个改变量越小越好。从恢复与保护生态的角度出发,王学敏等[17]研究了以生态溢缺水量最小为生态目标的优化调度模型,但研究重点是提出了一种双种群多目标差分进化算法和不同调度方法方案之间的对比,对生态溢缺水量没有做详细解释。顾然[18]研究了为生态径流定上下限约束的调度模式,并量化定义了溢水量和缺水率的百分比,提出多种试探性调度方案比较优劣。赵越[19]针对长江中游生态环境修复的需求,得到河段流量-加权可用面积关系曲线,并在多目标调度模型中加入了生态溢缺水量最小作为目标。然而受到资料的限制,将该模型仅应用于长江中游葛洲坝下中华鳃产卵场,仍需进一步验证适用性。如何确定及控制生态径流可改变的量,并在水资源管理利用中尽量使偏离适宜生态需水区间的水量越小,成为当下面向生态友好的水资源管理研究的关键。
针对以上问题,本文以浊漳河流域为研究区,建立水库群生态调度模型,以大系统分解协调技术求解模型。该模型综合考虑了生态需水的处理,通过设定适宜生态流量上限和下限,使下泄量尽可能落在这个区间内,提出以生态溢缺水率最小作为一个目标;将必须满足的子系统的基本生态需水和下游的生态需水作为约束代入模型。
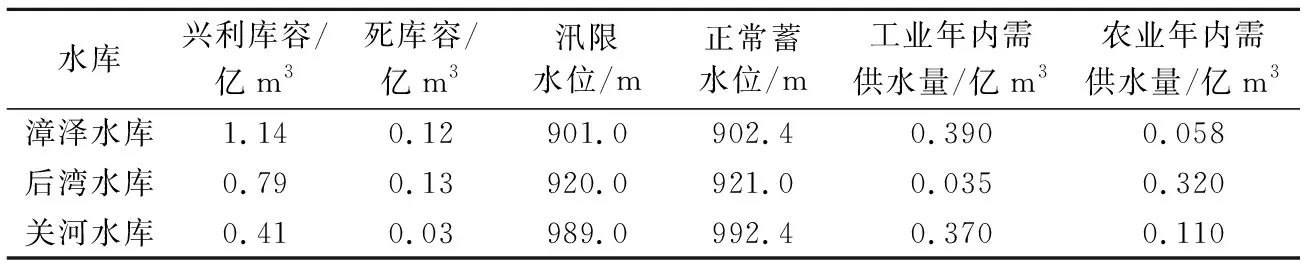
表1 研究区三大水库基本数据Table 1 Basic data of three reservoirs in the research area
1 研究区概况
浊漳河流域位于山西台地东侧,呈扇形分布,有南、北、西三大支流,称浊漳南源、浊漳北源、浊漳西源,三源径流主要由漳泽、关河、后湾三大水库分别控制。水库建设初期,污水直接排入河道中,造成严重污染和生态破坏,流域内河流枯水季节多有断流现象。
漳泽水库是一座多年调节水库,担负着下游县(市)及部分厂矿企业的防洪和供水任务。后湾水库是一座多年调节水库,担负着长治市部分工业供水任务。关河水库是一座年调节水库,水库多年平均天然径流量1.85亿m3,来水量大,主要担负防洪任务。用相关法和需水量弹性系数法计算了近期年工业需水,用直接计算法计算了农业需水,三大水库的主要数据见表1。
为发挥库群最大效益,本文共划分4个计算河段,即三大支流与干流,按水库供水任务划分3个基本用水单元,即生态、农业和工业供水分别概化不同的取水口。研究区水资源概化如图1所示。
2 生态需水分析
本文将水文情势变化在允许程度范围内,对河流生态系统具有恢复和保护作用的要求流量作为生态环境目标,涵盖维持河道不断流以及保障生物多样性等。本文采用漳泽、后湾、关河三大水库1968—1998年的径流数据(数据来自山西省水资源管理中心及水文年鉴),以月尺度进行研究。
2.1 生态溢缺水量
天然状态下,径流的类型和时空变化规律较为稳定。稳定的自然径流是最优的生态径流量,所以有必要使调度后的径流尽可能接近自然径流。而生态需水量本身是一个阈值范围[20-21],适宜的生态流量也应该有上下限范围,调度后的下泄流量应尽可能地落在这个区间内。
在传统的面向生态友好的水资源管理中,多用生态缺水量表征和控制生态水量,为达到贴近自然稳定的一个区间效应,增加了生态溢水量的概念,即超过一定的上限,就认为是溢出水量。为使调度后的径流尽可能接近自然径流,选用生态溢缺水量作为竞争目标,认为当河道内流量低于适宜下限或者高于适宜上限时,将会对河流生态系统的稳定性造成影响。
2.2 生态需水计算
经查阅国内外相关文献,针对较大的时间尺度的生态需水计算,Tennant法较为常用。但综合水文情势的要素来看,此法仅考虑了流量大小和发生时机。为此,本研究在使用Tennant法进行生态需水计算的同时,引入基于RVA框架的逐月频率法分析月尺度下的生态径流过程并与前者进行对照[18]。此法经过了赵越[19]、许可[22]、王学敏[23]的实践分析,由于篇幅所限,不做具体介绍。
根据研究区水资源特点和发展水平,参照SL/Z 712—2014《河湖生态环境需水计算规范》,在Tennant法计算中,适宜生态需水量上下限分别取“极好”与“好”等级,基本生态需水取“中”等级;基于RVA框架的逐月频率法中,适宜生态需水量上下限分别取80%、20%逐月频率,基本生态需水取10%逐月频率。计算得到适宜生态需水量范围如表2所示。
3 水库群生态调度模型的建立
3.1 目标函数
本文的经济目标包含工业生产和农业灌溉两方面;社会目标原考虑生活供水目标,但山西省水资源管理中心提供的资料显示研究区水库不提供生活用水,所以本文不考虑生活供水目标;生态环境目标涵盖维持河道不断流、保障生物多样性等。因此,水库生态调度的最终目的就是综合考虑流域水资源系统综合供水的缺水率最小。
3.1.1 工业、农业目标
(1)
式中:fi,j——i水库j目标寻优后的缺水率;αi,t,j——i水库在第t时段j目标的权重;Di,t,j——i水库j目标在第t时段的需水量;qi,t,j——i水库t时段给j目标的供水量。
3.1.2 生态目标
为使目标均为无量纲的缺水率,将生态溢缺水量最小改进为生态溢缺水率最小。
(2)
式中:Ei,t——i水库在第t时段的生态溢缺水率;Wi,t——i水库在第t时段的适宜生态流量下限。
以上目标函数的设定还有一个好处,若下泄量远远大于适宜生态需水上限 ,平方项将放大差距,在寻优中自动剔除,是一种不需要设置惩罚因子的处理方法。
3.1.3 综合缺水率评价函数
(3)
式中:Fi——i水库的综合缺水率。
3.2 约束条件
Vi,t+1=Vi,t+Qi,t-ui,t
(4)
(5)
minui,t≤ui,t≤maxui,t
(6)
VS,i≤Vi,t≤VL,i
(7)
Qx,t≥Dx,t
(8)
式中:Vi,t——i水库t时段的蓄水量;Vi,t+1——i水库t+1时段初的蓄水量;VS,i——i水库的死库容蓄水量;VL,i——i水库的兴利库容蓄水量;Qi,t——i水库t时段的入流量;Qx,t——下游断面t时段的来水量;ui,t——i水库t时段的下泄量;Bx,i,t——i水库与下游段面在t时段的区间来水量(包含回归水量);Dx,t——下游段面t时段的生态需水量。
4 模 型 求 解
本文使用大系统递阶控制和分解协调技术依据强对偶定理将流域内三大水库多年优化调度的大系统分解为几个较为简单的子系统,子系统内用DP法求解。由于空间分解后形成的子问题仍是一个较复杂的问题,所以在时间上再进行一次分解,将时间子问题套接在空间分解的子系统上,如图2所示。
4.1 空间分解
在空间分解中,并联的三大水库各自作为一个子系统,由于并联水库之间没有水力联系,而各子系统的水量平衡等式约束一定满足,可不予考虑,而将三大子系统共同承担的生态供水任务作为耦合变量添加KKT乘子构造拉格朗日函数:
(9)
式中:γt——式(9)的KKT乘子;Vd,i,t——i水库t时段扣除自身需要供应的工业、灌区等用水户用水后下泄到下游的水量。
对于协调级本文采取自动调节步长的最速下降法进行协调变量的寻优,力求减少协调级的计算次数。在协调级有:
(10)
由此可得空间协调的协调级的迭代计算公式为
(11)
式中:γk+1,t——第k+1次迭代;γt——第k次迭代;S——协调级的计算步长,由数量级确定。
对于收敛条件的判断,先判断是否满足KKT条件,或计算结果不随迭代次数变化或变化很小,即
|γk+1,t-γt|≤ε
(12)
4.2 时间分解
为使年际缺水率尽量趋于平均,需进行时间分解。把调度期分成Y段,相应地有Y个子系统,本文选择每一年为一个子系统。在时间分解中,加入时间关联约束:
Vi,y+1=Vi,y+Qi,y,12-ui,y,12
(13)
式中:Vi,y+1——i水库y+1年的年初蓄水量,;Vi,y——i水库y年第12月月初的蓄水量;Qi,y,12——i水库y年最后一个月的来水量;ui,y,12——i水库y年最后一个月的下泄水量。
不考虑子系统本身的约束,将上一年的年末蓄水量与下一年的初始蓄水量作为耦合变量添加Lagrange乘子构造拉格朗日函数:
(14)
式中:βi,y——式(4)、式(5)的拉格朗日乘子,即时间协调因子;Fi,y——i水库y年的综合缺水率。
协调因子与水库供水的边际效应可以使年际缺水率趋于平均,当y时间段与y+1时间段的缺水率之差大于允许范围时,协调因子βi,y作为一个惩罚协调使年际缺水率差值在允许范围内。
最终收敛判别条件为:各约束条件均能满足、年际缺水率差值在允许范围内或者计算结果不随迭代次数变化或变化很小。
5 结 果 分 析
根据水库群生态调度模型的求解结果,得到漳泽、后湾、关河水库的库容、下泄和缺水率变化曲线,如图3、图4所示。
由图3可知,除1976年、1985年等极丰水年的汛期关河水库有大量弃水外,三大水库的下泄量基本上在各自承担的总需水量附近波动。当关河水库来水量较大产生较多弃水时,漳泽与后湾水库在满足自身需水量外,承担了较少的下游生态需水,并在来水量较大时尽可能蓄水。
由图4可知,关河水库除1975年、1981年由于来水量较少导致缺水率较高外,其他年份都能完成供水任务。漳泽、后湾水库的年际缺水率也较为平均,说明本文模型很好地处理了年际间缺水不平衡的情况。
由图4可得,漳泽、后湾、关河水库的月平均综合缺水率为0.17%、0.73%、0.13%,即三大水库的供水任务几乎没有遭到破坏。为比较生态竞争目标分别为生态溢缺水率最小或生态缺水率最小时,何者更优。在本文模型的框架上,仅将生态竞争目标换为生态缺水率最小,其余目标与约束均不变,再进行了一次计算。结果得漳泽、后湾、关河水库的月平均综合缺水率为0.42%、1.35%、0.16%。容易发现,以生态溢缺水率最小作为生态竞争目标,漳泽、后湾、关河水库的月平均综合缺水率分别减少了0.25%、0.62%、0.03%。从水量平衡的角度思考,这是由于生态溢水量的竞争,使得一部分水量没有浪费,而是更加平均地分配到了枯水年补充用水,在时间尺度上优化了调度结果。
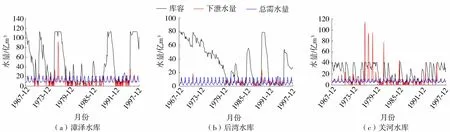
图3 三大水库库容、下泄水量及总需水量曲线Fig.3 Reservoir capacity, discharge volume and total water demand of the three major reservoirs
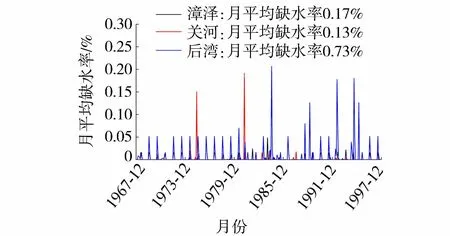
图4 三大水库缺水率变化曲线Fig.4 Water shortage rate curve of three reservoirs
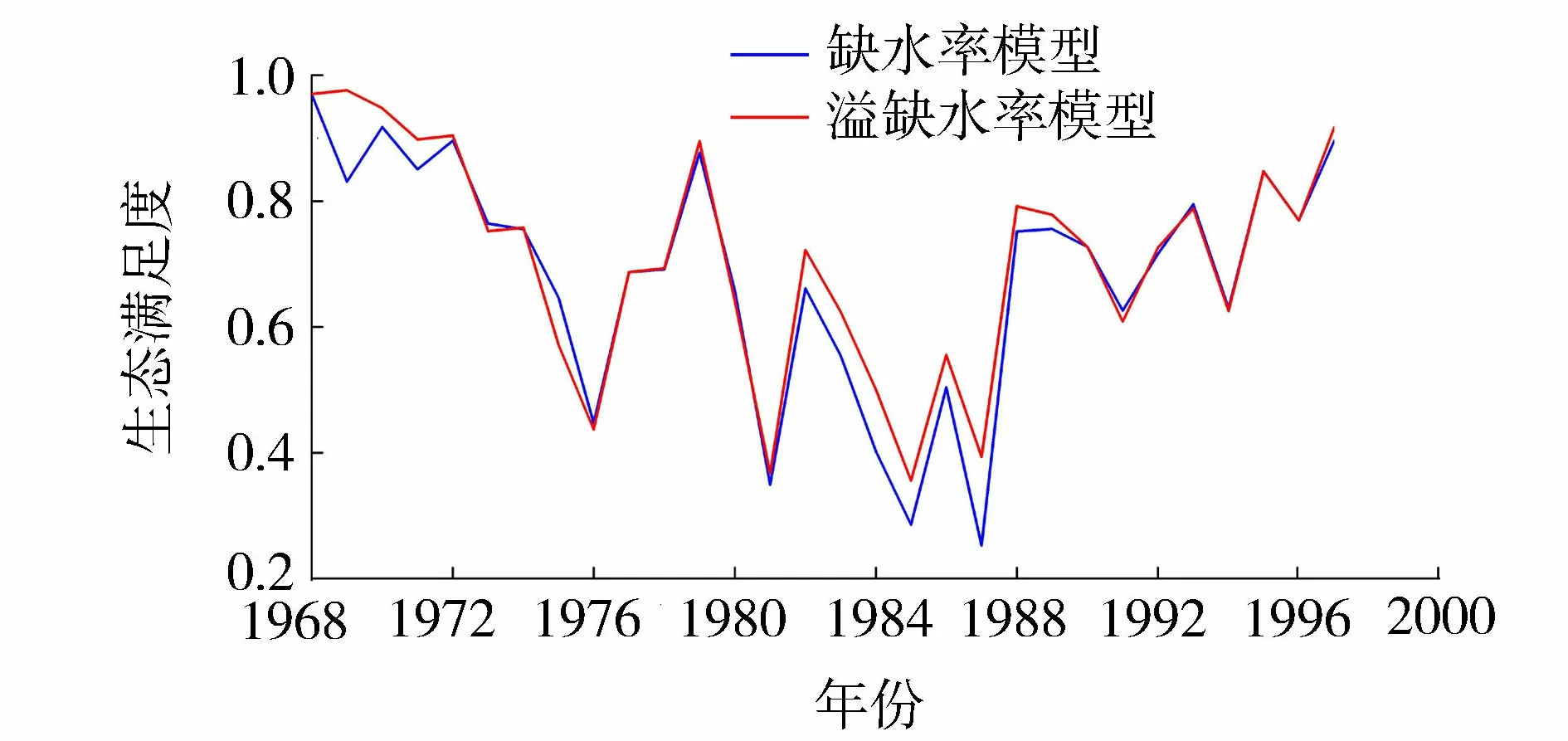
图5 生态满足度比较Fig.5 Comparison of ecological satisfaction rate
为方便比较,本文将生态满足度定义为满足适宜生态需水量范围的程度。若下游断面来水量在适宜生态需水量范围内,生态满足度为1;若来水量小于生态需水量下限,则生态满足度为来水量与生态需水量下限的比值;若来水量大于生态需水量上限,生态满足度为生态需水量上限与来水量的比值。以此定义,分别在缺水率模型和溢缺水率模型中进行计算,2个模型计算结果比较如图5所示。由图5可发现,正常来水年份2个模型差异不大,但在比较枯水的20世纪80年代,溢缺水率模型明显的比缺水率模型有更高的满足度。计算可得,溢缺水率模型和缺水率模型的多年平均生态满足度分别为70.8%和68.3%,多年平均生态满足度提高了2.5%,说明以溢缺水率作为目标可以更好地保护生态,可减少生态环境的破坏程度。
6 结 语
以生态溢缺水率最小、工业与农业缺水率最小为目标,建立了浊漳河流域水库群生态调度模型。该模型在时间上能很好地处理年际间缺水不平衡的情况以及空间上下游共同承担的生态供水任务,当漳泽水库由于兴利供水任务较重无法承担生态供水任务时,由关河水库增加下泄以完成下游的生态需水要求。通过比较分析以生态溢缺水率最小为目标和以生态缺水率最小为目标的结果差异,得出漳泽、后湾、关河水库的月平均综合缺水率分别降低了0.25%、0.62%、0.03%,多年平均生态满足度提高了2.5%,即以生态溢缺水率作为目标更优。

