基于神经网络的光伏电站气象-功率模型

鞠 平，刘婧孜，秦 川，李洪宇，杨宏宇，封 波，屈卫锋

(1.河海大学能源与电气学院，江苏 南京 210098； 2.国网连云港供电公司，江苏 连云港 222000；3.国网灌南县供电公司，江苏 连云港 223500)

近年来，随着一次能源的大量消耗及环境污染等问题的出现，光伏发电等可再生能源发电得到了快速发展。据统计，截至2018年底，我国光伏发电装机达到1.74亿kW，2018年全年光伏发电量达1 775亿kW·h[1]。光伏发电是一种典型的间歇式电源，其发电功率受气象、环境条件等的影响具有较强的随机性和波动性。光伏发电渗透率的不断提高对电网安全稳定运行的影响日益增强。建立准确的光伏发电功率模型并掌握其功率特性对电网和光伏电站自身的安全稳定运行具有重要意义[2]，常用的功率建模方法按模型描述方式分为机理和非机理[3]。机理方法基于辐照传递方程、光伏组件运行方程等通过系统内部工作过程的物理关系建立数学模型，非机理模型基于模型输入、输出因素间的统计规律建模[4-5]。常用的非机理模型包括传递函数(差分方程)模型、人工神经网络智能方法等[3, 6]。

人工神经网络因其具有高准确度和自学习的优势，所以在拟合系统的非线性输入输出关系特性时具有明显的优越性。Liu等[7]以待预测日与历史相似日的气温、湿度、风速及气溶胶浓度为输入，以待预测日有光照时段每小时输出功率平均值为输出，基于BP神经网络实现了对未来24 h光伏输出功率的多步预测。刘卫亮等[8]以PM浓度、温度、空气相对湿度等气象数据为输入，分别利用BP神经网络与SVM方法建立大气气溶胶光学厚度估计模型，基于精细天气预报信息和PM浓度的预测，实现对光伏发电超短期功率的预测。同样，基于BP神经网络，由欧式距离法确定天气类型，再结合光伏电站的历史出力数据将影响因素映射为天气类型指数，从而建立了计及天气类型指数的光伏发电短期出力预测模型[9]。 张程熠等[10]通过简化神经网络，降低输入输出维数，设计适用于小样本的双层神经网络单步光伏预测方法。可见，基于人工神经网络的光伏输出功率研究十分普遍[11]，大都集中于光伏输出功率的预测，但复现难度较大。而采用神经网络建立复杂气象因素与光伏输出功率间单纯关系的研究不多见，且对于建立的非机理模型精度的提升和神经网络结构参数设置的优化等问题，仍待进一步研究。

本文基于人工神经网络，以辐照、温度等气象因素为输入变量，光伏电站的输出功率为输出变量，建立光伏电站的气象-功率非机理模型。着重研究了神经网络结构、不同气象因素的组合作为输入对模型输出准确度的影响，明确了功率模型的理想网络结构与参数。最后基于实际光伏电站的量测数据，对提出的光伏电站气象-功率模型进行了对比验证。

1 数 据 采 集

由于光伏电池的材质特性，光伏电池的输出特性受气象因素的影响较大，特别是太阳辐照度和电池温度[12]，因此对光伏发电输出功率进行建模时，作为输入的气象因素中必须含有辐照度和温度。本文研究采用的数据包括气象数据、光伏电站实测功率数据等。

1.1 气象数据

研究采用的气象信息来自SolarGIS高分辨率气候数据库。采样地点同下文光伏电站处，采样时期为2017年全年，采样的时间分辨率为10 min。SolarGIS的数据为实地采样的平均值，并已成功应用于光伏发电的评估[13]，因此可以基于SolarGIS的气象数据对光伏电站输出功率建模。采集的数据包括水平面总辐照度(global horizontal irradiance, GHI,W/m2)、散射水平辐照度(diffuse horizontal irradiance, DHI,W/m2)、倾斜面总辐照度(global tilted irradiance, GTI,W/m2(倾角31°，方位角180°))、温度(air temperature, TEMP,℃)、风速(wind speed, WS, m/s)和风向(Wind direction, WD(°))。

受地理位置的影响，不同经纬度下具有不同的最佳太阳入射角[18]，因此为得到最大的光伏输出功率，光伏面板需要呈现一定的倾斜角。在进行光伏输出特性的相关研究时，同一地区可以采用相同的光伏阵列倾斜角[19]。

本文采用的其余气象数据(TEMP、WS和WD)由天气预报系统(climate forecast system reanalysis, CFSR)、第二版天气预报系统(climate forecast system Version 2, CFSv2)和美国气象服务系统(global forecast system, GFS)数值天气模型生成，其精度略低于辐照数据，全年不确定度分别为温度±1.3℃、风速±1.7 m/s，满足表征采集点地理区域内气象特点的精度要求。上述气象信息均得到NOAA综合地面数据库的验证。

1.2 光伏电站输出功率数据

研究采用的光伏功率数据为某实际光伏电站连接至上级变电站35 kV侧进线的有功功率Preal，数据时长为2017年全年，采样间隔为5 min。功率数据取自某地调的EMS系统历史数据库，数据精度满足工程要求。

1.3 数据预处理

由上述可知，实测气象数据为平均采样值，实测光伏电站输出功率为EMS系统实际量测值。在建模前首先对光伏功率数据预处理，将光伏电站输出功率采样的时间分辨率由5 min变为10 min，并对功率数据进行插值处理。预处理的步骤如下：

a. 将光伏电站输出功率数据与气象数据的采样时间点进行对应，确定预处理后将用于模型训练的数据采样时间点。

b. 选取该采样时间点及其前后各一个采样时间点的光伏电站输出功率数据，将3个采样数据加和并求均值。

任意选取某天2 h(例如8:05～10:05)内的倾斜面总辐照度与光伏电站输出功率数据，进行上述操作，得到预处理前后的数据结果如图1所示。由图1可以看出，对光伏电站输出功率的预处理可以描述光伏功率的总体变化特性。

在新闻语体中，新闻报道要做到真实客观，在修辞表达时就必须要做到表意准确严密，在时间、地点、人物、事件等的叙述方面就不能出现硬伤，不许弄虚作假，不许模模糊糊，不许模棱两可。黎运汉、盛永生认为，准确性是新闻语体的首要要求和基本特点。要做到表意准确，就必须在遣词造句、相关数据的使用、模糊语言的使用、引语的使用等方面下足功夫，做到准确可靠。[2]179-182例如：

2 光伏电站气象-功率模型的神经网络结构

2.1 双层前馈神经网络

本文采用的双层前馈神经网络是基于sigmoid隐含层神经元和线性输出神经元的网络[20]，由输入层和计算层构成，其中计算层包括隐含层和输出层。该神经网络在给定一致的数据和足够的隐含层神经元后经过反复训练，即可很好地拟合多维映射问题[21]。

适用于双层前馈神经网络的训练算法很多，其中常见的如Levenberg-Marquardt、Bayesian Regularization和Scaled Conjugate Gradient。限于篇幅，详细计算过程可参考文献[22-24] 。

神经网络输入层和输出层节点数与网络的特征和目标的维度匹配，并影响隐含层神经元个数。一般而言，当输入层节点为m个且各输入变量不具有关联性时，隐含层节点为(2m+1)个。但隐含层节点数也可由设计者设定。双层前馈神经网络的拟合原理在2.2节中结合实际数据详细说明。

神经网络的估算效果由网络的均方根误差(root-mean-square error,ERMSE)和绝对值均值相对误差(absolute mean relative error,EAMRE)体现，计算公式分别如式(1)和式(2)所示。2种误差各自的数值越小，模型效果越好。

(1)

(2)

2.2 功率模型的基本结构

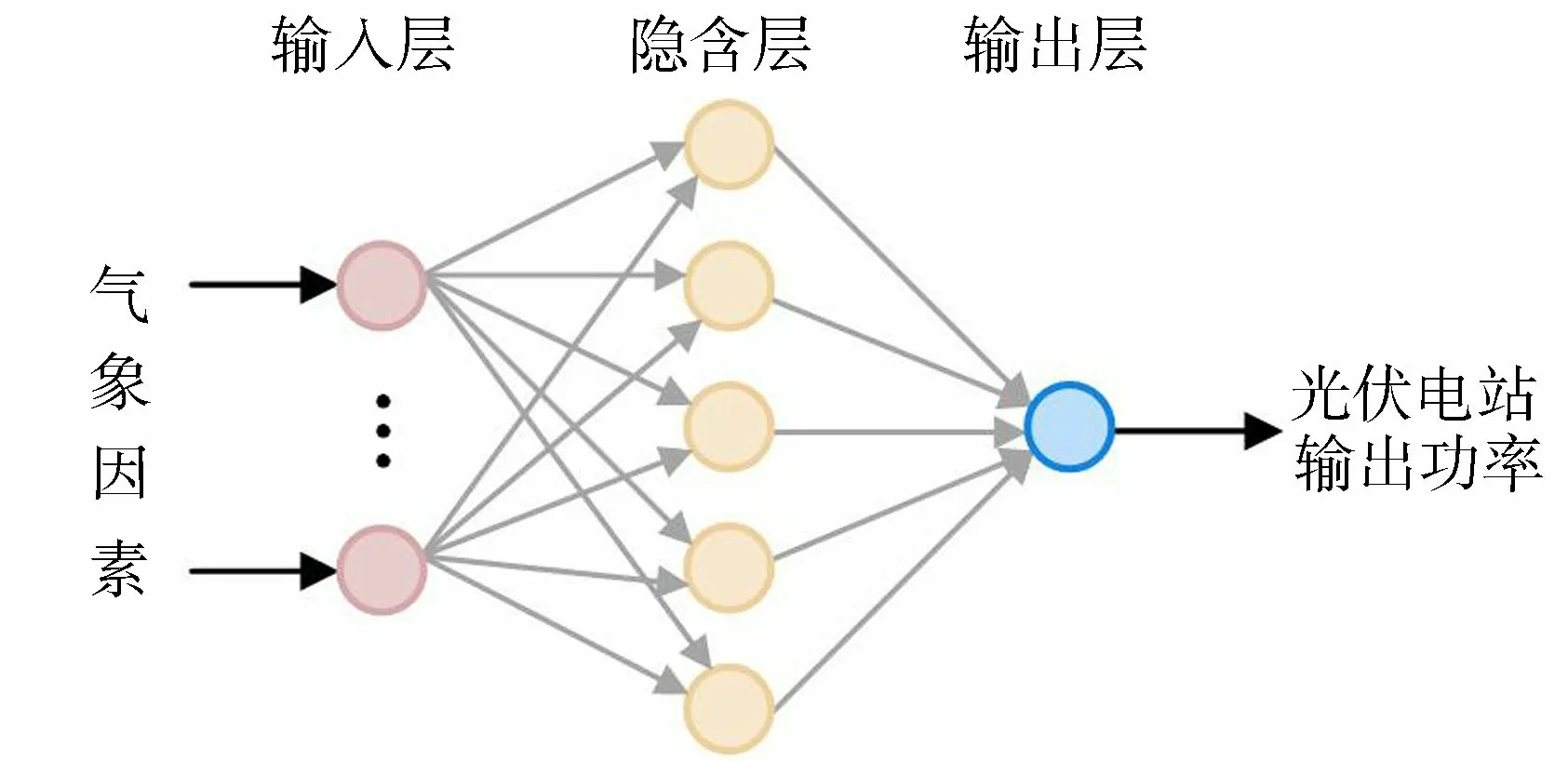
图2 基于神经网络建模的结构Fig.2 Structure chart of model based on two-layer feed-forward neural network

研究借助MATLAB，采用双层前馈神经网络建立光伏电站输出功率与多气象因素之间的非线性模型，该光伏电站气象-功率模型的神经网络基本结构如图2所示。模型的输入为各种气象因素，输出为光伏电站的输出功率，网络结构为包含一层隐含层的前馈神经网络。

网络的训练、验证和测试过程如下：

a. 训练：随机选取70%的样本集作为训练集训练网络。

b. 验证：在剩余的30%样本集中随机选取1/2的数据(总样本集的15%)作为验证集验证网络，当验证集的误差收敛后停止训练，得到此时拟合效果突出的网络权重参数。

c. 测试：将剩余15%的样本集作为测试集，以该网络测试误差的形式表现上述确定的网络的性能。

在建模过程中，气象因素输入组合和网络结构的不同会对功率模型的精度产生较大的影响。为了得到准确的光伏电站气象-功率模型，下文将对功率模型的输入特征进行选择，得到效果理想的功率模型。

3 光伏电站气象-功率模型的输入特征选择

实际环境中含有丰富的气象因素，不同气象因素间会相互作用并且均对光伏电站的输出功率产生影响。本节对功率模型的输入特征进行选择，明确该功率模型理想的输入变量。在进行特征选择时，网络的初始隐含层神经元为5个。

3.1 辐照作为神经网络输入

通常意义下，辐照是影响光伏电池输出功率的主要因素，而实际环境中存在多种类的辐照，因此首先设置不同类型的辐照组合作为神经网络的输入，对比各组网络的准确度。设置5组不同类型的辐照作为输入的对照组分别为：倾斜面总辐照度；水平面总辐照度；散射水平辐照度；水平面总辐照度+散射水平辐照度；倾斜面总辐照度+水平面总辐照度+散射水平辐照度。将5个对照组依次进行训练，得到对应神经网络的均方根误差分别为1.178 6 MW、1.462 7 MW、2.857 6 MW、1.403 7 MW、1.124 4 MW。由此可知：(a)将3种辐照度组合作为神经网络输入时，网络误差最小;(b)以倾斜面总辐照度作为输入时的误差略大于3种辐照度组合，但明显小于其他2种辐照度的组合。可见，由于光伏面板呈现倾斜状态，其吸收最充分的辐照是倾斜面总辐照度，所以倾斜面总辐照度为影响光伏电站输出功率的最主要气象因素。

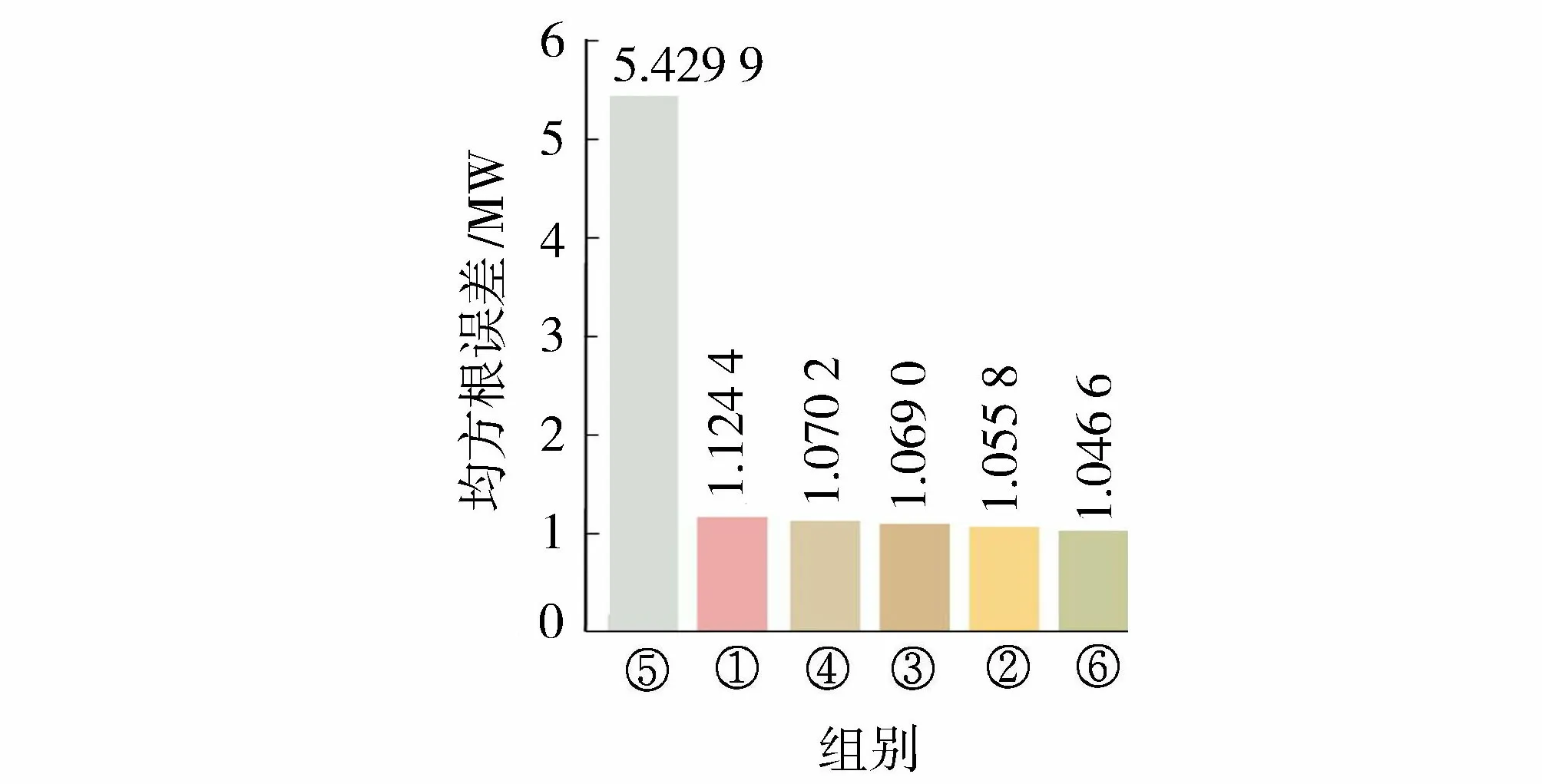
①—倾斜面总辐照度+水平面总辐照度+散射水平辐照度；②—倾斜面总辐照度+水平面总辐照度+散射水平辐照度+温度；③—倾斜面总辐照度+水平面总辐照度+散射水平辐照度+风速；④—倾斜面总辐照度+水平面总辐照度+散射水平辐照度+风速+风向；⑤—温度+风速+风向；⑥—倾斜面总辐照度+水平面总辐照度+散射水平辐照度+温度+风速+风向图3 功率模型在6组不同网络输入特征下的均方根误差Fig.3 RMSE of power models with 6 different input features

3.2 温度和风况作为神经网络输入

对比神经网络输入中加入温度和风况气象因素的影响。设置6组不同输入的对照组，并依次进行训练，得到每组对应的神经网络的均方根误差，如图3所示。

从图3中可以看出：(a)仅以温度和风况作为输入(组⑤)的误差最大；(b)由于光伏面板为光敏温敏材料，而经过其表面的风况又能影响温度和辐照。因此，将所有的气象因素作为功率模型的输入(组⑥)，误差最小。

综上，后续对光伏电站功率建模研究中，输入因素设定为全气象因素。而如果实际情况下部分气象因素未知，可以考虑倾斜面总辐照度与已知气象因素的组合。

4 光伏电站气象-功率模型的结构优化

4.1 神经网络的理想训练算法及训练次数的选择

不同的网络训练算法对功率模型的训练和应用也会有影响。双层前馈神经网络常见训练算法如Levenberg-Marquardt、Bayesian Regularization和Scaled Conjugate Gradient算法。按照上文选定的神经网络输入输出变量，依次在3种训练算法下进行1～40次独立训练，统计每种训练算法在完成1～40次训练后的网络均方根误差，如图4中的散点所示。

图4 功率模型在不同算法和训练次数下的均方根误差分布Fig.4 Scatterplot of RMSE of power model with different training algorithms and training times

由图4可以看出输入输出一致的神经网络进行多次训练时结果误差存在明显差异，模型估算结果的误差呈现波动状态，这是因为神经网络的初始权重为随机设置，导致优化的网络权重存在随机性。标记多次独立训练后均方根误差最小值，如图4中的实线所示。

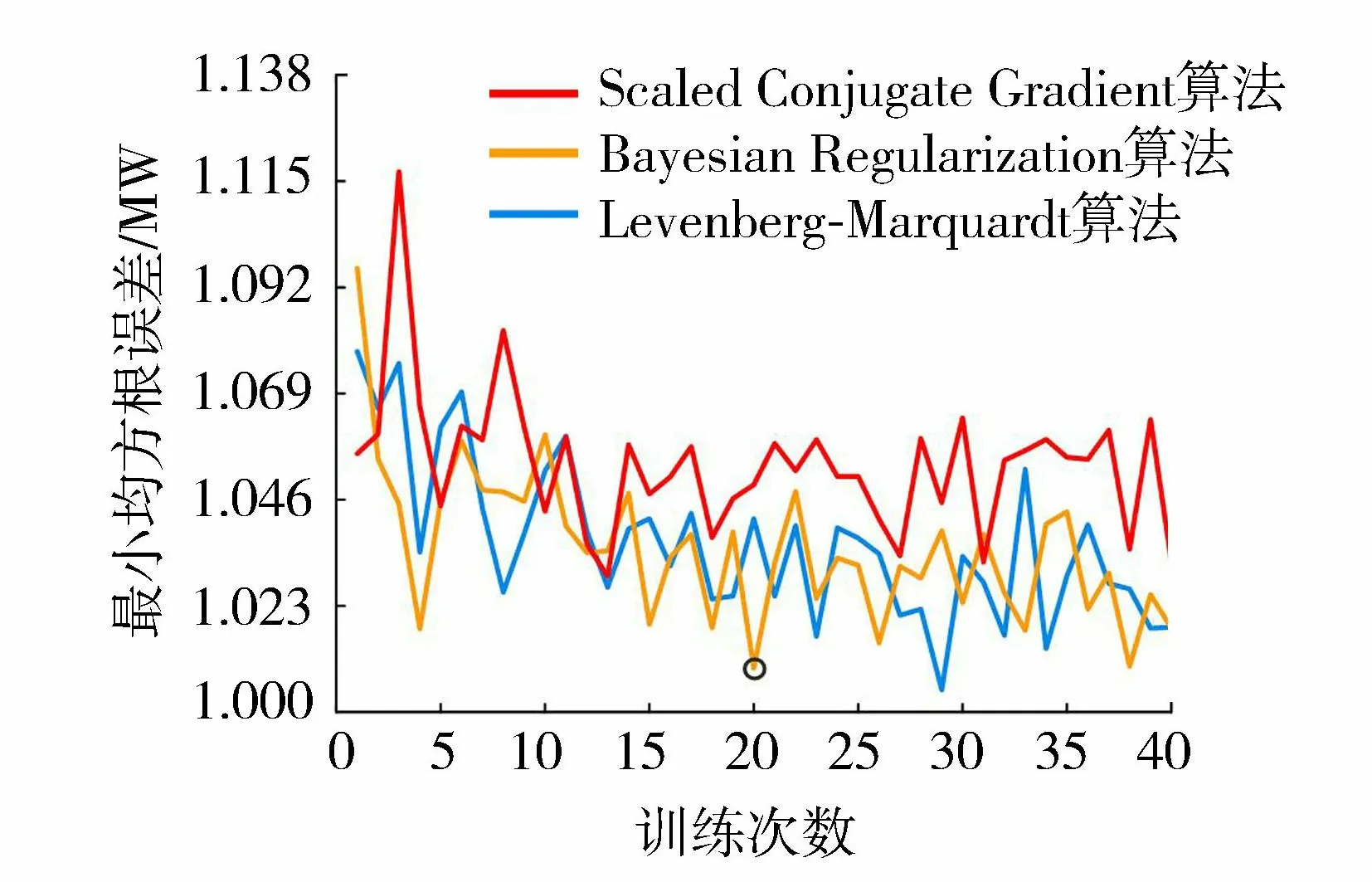
图5 3种训练算法在不同训练次数下的最小均方根误差曲线Fig.5 Curve of minimum RMSE with 3 training algorithms under different training times

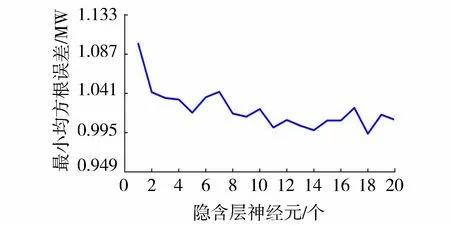
图6 不同隐含层神经元的最小均方根误差分布Fig.6 Scatterplot of minimum RMSE with different hidden layer neurons number

将图4中3条实线进行对比，如图5所示。可以看出整体上基于Scaled Conjugate Gradient算法的均方根误差最大，Levenberg-Marquardt算法的误差和Bayesian Regularization算法的误差接近，但Levenberg-Marquardt算法的误差波动相对大一点。此外训练过程中发现Bayesian Regularization算法的训练时间最长，Scaled Conjugate Gradient算法所需的训练时间次之，Levenberg-Marquardt算法的最短。虽然Levenberg-Marquardt算法在经过29次训练后可以得到误差最小的网络，对该误差相比Bayesian Regularization算法20次训练后得到的网络误差(图5中黑色圆圈处)没有明显的提高。同时，基于Bayesian Regularization算法的网络在训练次数达10次后，波动趋势趋于稳定。

综上，采用Bayesian Regularization训练算法进行20次训练，随后选择其中均方根误差值最小的网络可相对理想地拟合该光伏电站输出功率与气象因素的关系模型。

4.2 神经网络的理想隐含层节点数的选择

隐含层节点数设定过少时，神经网络不能充分发挥学习能力和拟合能力；隐含层节点数设定过多时，增加网络结构的复杂性，导致网络学习训练过程耗时，学习过程中容易陷入局部最优解。基于上述确定的双层前馈神经网络的输入变量、训练算法和训练次数，依次设置隐含层神经元为1～20个训练神经网络，统计各组的均方根误差最小值，如图6所示。各组进行20轮训练的耗时如下：隐含层节点2个,总耗时80 s;隐含层节点4个,总耗时198 s;隐含层节点6个,总耗时475 s;隐含层节点8个,总耗时670 s;隐含层节点10个,总耗时986 s;隐含层节点12个,总耗时1 302 s;隐含层节点14个,总耗时1 885 s;隐含层节点16个,总耗时2 195 s;隐含层节点18个,总耗时3 194 s;隐含层节点20个,总耗时3 239 s。

由图6可以看出，神经网络的均方根误差随隐含层节点数的增加而呈现减小的趋势，10个隐含层节点后，波动趋势趋于稳定；神经网络的总耗时与隐含层节点数之间呈现正相关的关系；隐含层神经元为14个和18个时的神经网络均方根误差明显较小，对比耗时，确定隐含层神经元为14个。

综上，本研究中功率模型的理想网络结构为：隐含层神经元为14个、采用Bayesian Regularization训练算法进行20次训练，随后选择其中均方根误差值最小的神经网络。

5 模 型 验 证

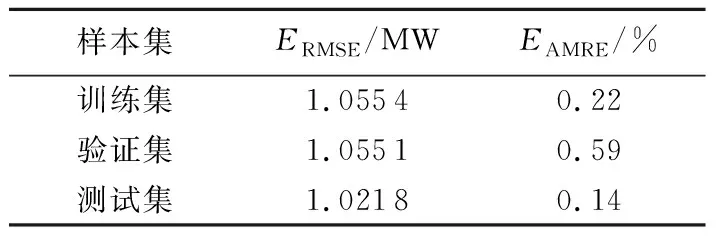
表1 功率模型的神经网络误差Table 1 Errors of power model based on neural network

根据上文的分析，建立光伏电站气象-功率模型的理想结构和参数，下文基于实际数据对该模型进行验证。功率模型的平均误差如表1所示。可以看出，由于训练集、验证集和测试集的样本数不同，三者误差也略有不同，但均小于1%，可见该光伏电站气象-功率模型具有良好的精度。

进一步在2017全年4个季节中分别随机选取晴天、阴天和多云的一天反映功率模型的估算效果，功率对比曲线如图7所示，选取的各随机天的估算结果误差如表2所示。

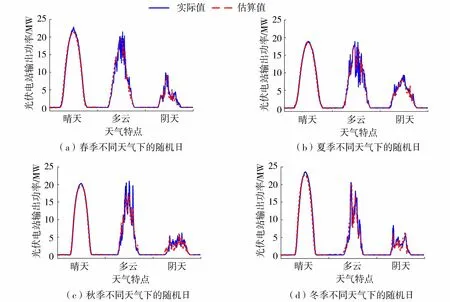
图7 基于光伏电站气象-功率估算模型的仿真结果对比Fig.7 Comparison of simulation results based on weather-power estimation model of PV plant

表2 基于光伏电站气象-功率模型的随机天误差Table 2 Errors of testing day based on weather-power estimation model of PV plant

由图7和表2可以看出：(a)该光伏电站气象-功率模型的计算结果与实际的功率曲线趋势一致；(b)晴天日的误差值很小，多云和阴天的估算结果略差于晴天，但除了春季阴天日误差达到9%以外，其余误差均小于6%。可见，本文所建立的基于双层前馈神经网络的光伏电站气象-功率估算模型可以理想地实现气象因素对光伏电站输出功率的估算。

6 结 语

基于双层前馈神经网络，建立了光伏电站气象-功率模型并进一步改进提高了模型的精确度。首先，对功率模型的输入特征进行选择，明确了对光伏功率影响最大的气象因素是倾斜面总辐照度;其次为水平面总辐照度,尽管温度和风况对功率估算的影响较小，但较全面的气象因素输入可以使神经网络模型达到较好的估算效果;再次，通过神经网络的不同的训练算法、训练次数及隐含层节点数对比，确定了功率模型的网络结构和参数;最后，通过实际光伏电站的量测数据，对建立的功率模型进行了验证。结果表明，该光伏电站气象-功率模型具有良好的精度。