关于机械横波反射与折射的演示实验

路峻岭 顾 晨 秦联华 任乃敬 马泊一

(清华大学物理系，北京 100084)

1 筷波仪简介

图1 筷波仪照片图

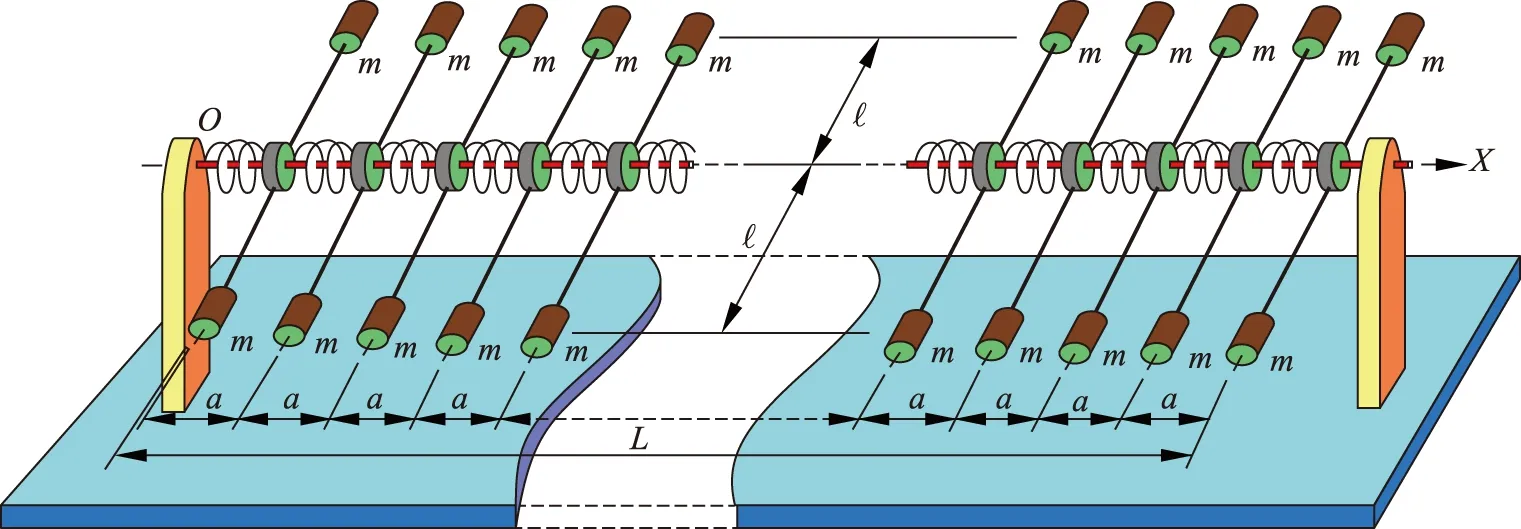
图2 筷波仪振子链的示意简图

筷波仪的照片如图1所示，它由用以演示机械横波的振子链、激励电机(上游源头)、阻尼器(下游尾端)和激励电源、止动电源等几部分组成[1]。振子链由一串可绕一根水平细轴转动且相互弹性连接的振子串组成，示意图如图2所示。每一个振子都可以绕水平细轴作微幅转动振动，振子链上可以产生以振子转动角度为参量的机械波。从仪器的侧面观察，振子的端部则表现为横波波动。由于每一个振子都像一根筷子，所以这种仪器又称为筷波仪。开启激励电源，上游源头(x=0)开始振动，由于振子之间的弹性连接，于是在振子链上出现波动。如果调节阻尼器使下游尾端(x=L)的阻尼适当，波动传播过来的能量被完全吸收，则振子链上的波就是行波。如果除去阻尼器使下游尾端固定或自由，则在振子链上将出现驻波。如果想瞬时固定住波列波形，就开启止动电源，此刻波列就会被突然冻住。不过，这一操作只能在几秒内结束，否则容易损坏仪器。本文所涉及的实验是改变部分区段(如下游区段)振子的转动惯量，以使振子链的波阻抗发生改变，演示波阻抗改变对机械波传播的影响。

2 筷波仪振子链上的机械波

筷波仪振子链的结构如图2所示，设诸振子结构均匀一致，振子端部小圆柱体的质量皆为m，其质心离水平细轴的距离皆为l，相邻振子之间的距离为a，则每一个振子的转动惯量约为2ml2，沿轴向单位长度上振子链的转动惯量即转动惯量密度2ml2/a，设振子链的总长度为L。沿水平轴方向建立x轴，如图2所示。

2.1 筷波仪上振子链的波动方程及其解[2-3]

设筷波仪振子链在自然状态(不受任何外力)时，处于水平位置，操作者拨动最右端(x=L)的振子，施加力矩M使它偏离水平位置的角度(扭转角)为θ，并设振子链的力矩弹性系数为K，则根据胡克定律，有

M=-Kθ

(1)

这是在振子链均匀扭转形变的情况下，得到的力矩-形变的关系式。若振子链中有波存在，整个振子链就不会处处形变均匀了。现在考察振子链中某一点两侧振子链元段之间的相互作用力矩。上例表示整个振子链在力矩M的作用下扭转角为θ，整个振子链扭转应变为θ/L。由于振子链均匀，扭转应变处处相同，而且振子链中任意一点两侧元段之间的相互作用力矩均为M，因此有

(2)

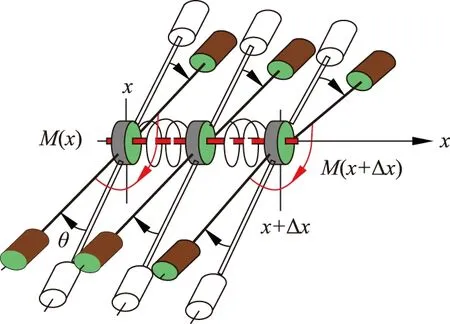
图3 振子链元段的应变与力矩

振子链元段Δx上的所受合力矩为

由定轴转动定律,得

即

(3)

(4)

其中A为振幅，ω为波的圆频率，c为波速，k为波数，波数k前面的符号±表示波的传播方向，正号表示往负x方向传播的行波，负号表示往正x方向传播的行波。一般来说，波动方程在具体条件下的解是这两种行波的线性叠加。易证明上述波动函数θ(x,t)确实是波动方程的解，但ω与k这两个参数并不独立，它们必须满足下列方程式：

(5)

在具体问题中，例如振子链两端固定，这些物理边界条件必然限定了k不能任意取值，只能取一些分立值，由此定出频率ω也是分立的，这些我们在柔弦振动实验中已经知道了。

2.2 筷波仪上机械波的波阻抗

日常生活中人们有一个直觉，就是骑自行车遇到逆风或爬坡时，尽管可以慢登，但依然觉得很吃力。如果自行车装上了加快轴(齿轮变速装置)，换一个挡，加快登车的速度，即使功率不变，也会觉得轻松得多。又例如游泳时，由于人的手掌脚掌面积不够大，尽管很快划水，但总觉得使不上力，若在脚上穿上蛙蹼，用力大一点，即使划慢一点也能得到同样的功率，游得很快，人会觉得很自在。这里涉及一个概念，就是阻抗匹配问题[2]。

力学中的功W=f·s;W=M·θ；

=f·(恒力时)；

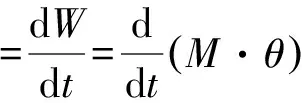
电学中的功率p=VI。

θ0(x,t)=Acos(ωt-kx)

(6)

在振子链上选一点x，我们计算x点负侧(上游侧)对正侧(下游侧)的作用力矩，以及x点处振子振动的角速度。

(7)

定义波阻抗Zc为力矩除以角速度。则有

(8)

若振子链中存在负向行波θ1(x,t)=Acos(ωt+kx)，x点正侧(上游侧)对负侧(下游侧)的作用力矩和角速度为

图4 两种阻抗的振子链

(9)

可见波阻抗只与载波介质的物理特性有关，而与波的传播方向、波的频率、波的波数等波动参量无关。若载波介质在某一点上的物理特性有突变，即波阻抗有突变，对波的传播有何影响呢？

2.3 筷波仪振子链上的机械波在阻抗突变点的反射与折射

设入射波为θ0(x,t)=Acos(ωt-kx)(-L/2≤x≤0);反射波为θ1(x,t)=RAcos(ωt+kx)(-L/2≤x≤0);折射波为θ2(x,t)=TAcos(ωt-k′x)(0≤x≤L/2)，其中R为振幅反射率，T为振幅折射率。在上游区段(x≤0区段)，振子链中存在着两个波,即θ上(x,t)=θ0(x,t)+θ1(x,t)。在下游区段(x≥0区段)，振子链中存在着一个波(不考虑尾端的反射),即θ下(x,t)=θ2(x,t)。

x=0点为两种阻抗区段的边界点，边界条件是：两边介质在边界点的相互作用的力矩大小相等方向相反;两边介质振动在边界点的角位移相等。其数学表达式(边界条件方程)如下。

(10)

具体到本问题, 边界条件方程即:

根据边界条件方程(11)，两边介质扭转振动在边界点的角位移相等,即

θ上(0,t)=θ0(0,t)+θ1(0,t)=θ下(0,t)=θ2(0,t)

即

即

Acosωt+RAcosωt=TAcosωt

(13)

由此解出

T=1+R

(14)

由式(13)亦可知，两种阻抗的区段的扭转振动在边界点不仅角位移相等，角速度也相等。为了计算波阻抗，只要用式(12)的两边之一除以角速度即可。不过用左边和用右边除以角速度计算波阻抗的物理意义不同。若用式(12)的右边除以角速度得到波阻抗,就是通过一列行波计算振子链波阻抗的过程,也就是类似式(7)、式(8)的计算过程。这如同电学中,由负载电阻两端的电压和通过负载电阻上的电流来计算负载电阻的值。若用式(12)的左边除以角速度得到波阻抗,就如同用电池的输出电压除以输出电流来计算负载电阻的电阻值。后者的优点在于它能够帮助把负载阻抗ZL、振幅反射率R和振幅折射率T都联系起来。以下按这种方法进行计算。

(15)

所以，负载阻抗

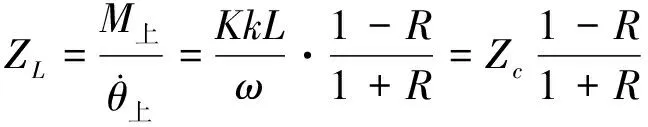
(16)

即

(17)

由此可见，振幅反射率R与负载阻抗ZL和源段阻抗Zc有关。把式(17)代入式(14)可以得到振幅折射率T。

即

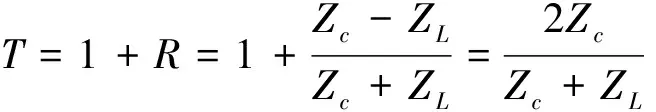
(18)

这样，我们就通过源段波阻抗Zc、负载阻抗ZL把振幅反射率R，振幅折射率T都表达出来了。由式(17)式(18)，我们可以看出: 振幅折射率T总是大于零的，表示在阻抗边界点，折射波的相位与入射波的总是相等的；而振幅反射率R却不同，它可正可负。在低阻抗边界(ZLZc)反射时，R小于零，表示反射波的振幅即有符号的变化，正号变为负号，相当于相位有180度的变化，如同波列突然减少了半个波长一样，称为半波损失。

2.4 筷波仪振子链上的机械波在阻抗突变点的反射波与折射波的能量分析

我们知道，根据能量守恒定律，入射波的能流密度应该等于反射波的能流密度与折射波的能流密度之和。首先我们先要看一个行波的能流密度如何表示[4]。

由此可得

(19)

这就是通过波阻抗、振幅反射率和振幅折射率表示的能量守恒定律。

由式(17)(18)

进而反射波与入射波的能流密度之比σ反

(20)

折射波与入射波的能流密度之比σ折

(21)

图5 R、T、σ反及σ折与阻抗之间的关系图

由图5可见，反射波的能流不会大于入射波的能流，只有在ZL=0，即边界为自由端、或ZL=∞即边界固定时才为1；其它情况下能流的反射系数均小于1。由于反射波能流与折射波能流二者之和总是等于1，两者各自所占比率亦如上图所示。振子链上波的特点是：在接近阻抗匹配时以折射波为主。在远离阻抗匹配时以反射波为主。

3 筷波仪振子链上的机械波在阻抗突变点的反射与折射演示实验

本实验欲演示振子链上机械横波在阻抗突变点x=0处的反射与折射(参见图4)。为了观测方便，我们在下游(折射区段)尾部设置阻尼器,调整阻尼使下游折射区段波动传输来的能量刚刚能被完全吸收。这样,在下游折射区段(x≥0)就只有一列正向行波; 而在上游区段(x≤0)就有两列行波: 入射正向行波和反射负向行波。本实验就是通过观察这三列行波组合的实验现象来了解机械波在阻抗突变点的反射与折射的。

设入射波为θ0(x,t)=Acos(ωt-kx)，反射波为θ1(x,t)=RAcos(ωt+kx)，折射波为θ2(x,t)=TAcos(ωt-k′x)，则在上游区段(x≤0区段)，其波列是两个行波的叠加,即θ上(x,t)=θ0(x,t)+θ1(x,t)；在下游区段(x≥0区段)，其波列是折射行波,即θ下(x,t)=θ2(x,t)。以下将按照高阻抗反射(ZL>Zc)和低阻抗反射(ZL

在高阻抗反射(ZL>Zc)时，由图5可知：-1

式(23)的推导中用到式(14)T=1+R=1-R′。可见，高阻抗反射时，在上游区段(x≤0区段)，入射波与反射波的叠加等效为一列驻波和一列行波的叠加。驻波的波节在波阻抗突变点x=0点；驻波波腹的振幅与振幅反射率的绝对值R′成正比；行波的振幅与折射行波的振幅相等；行波在阻抗突变点x=0点的位相与折射行波在阻抗突变点x=0点的位相完全相等并同步。在构成驻波的各振子作简谐振动都回到平衡位置的时刻，振子链上机械横波将表现为像是一列在阻抗突变点x=0处波数突变的行波。

在低阻抗反射(ZL

式(25)的推导中用到(14)式T=1+R。可见，低阻抗反射时，在上游区段(x≤0区段)，入射波与反射波的叠加等效为一列驻波和一列行波的叠加。驻波的波腹在波阻抗突变点x=0点；驻波波腹的振幅与振幅反射率R成正比；行波与驻波波腹的振幅之和与折射行波的振幅相等；行波在阻抗突变点x=0点的位相与折射行波在阻抗突变点x=0点的位相完全相等并同步。由于驻波在振子链上的位置是固定不变的，而行波的波峰是向x正方向运动的，在构成驻波的各振子作简谐振动都达到其振幅位置(偏离平衡位置最大)的时刻，振子链上机械横波将表现为像是一列振幅为入射波与反射波振幅之和且在阻抗突变点x=0处波数突变的行波。

由于增加振子链上振子的转动惯量较容易操作，我们只做了高阻抗反射(ZL>Zc)实验，就是只把下游区段(x≥0区段)每个振子端部的小圆柱体都增加了相同的质量。从实验现象看，将看到入射波的振幅经过阻抗突变点时一分为二，一部分为反射波的振幅，另一部分为折射波的振幅。这样，我们可以设想，把一束入射波分解为同步的两束波，一束振幅的大小等于反射波的振幅(甲波)，另一束的振幅等于折射波的振幅(乙波)。甲波与反射波的振幅相等，传播方向相反，两者的叠加形成驻波，阻抗突变点即为波节；乙波与折射波的振幅相等，传播方向相同，在阻抗突变点乙波突然变为相位相等但波数不同的折射波,如图6所示。

如果我们精确调节振子链尾端的阻尼器使阻尼适当，使折射波的能量被完全吸收，则振子链上高阻抗段的波就只有折射波行波。而低阻抗段的波则是振幅等于折射波的一列行波和一个振幅等于2倍反射波振幅的驻波的叠加。在驻波上各点都到达平衡位置的时刻，我们就可以看到像是上游低阻抗段的一列行波经过阻抗突变点突然变为幅度相同但波长不同的另一列行波。这一现象可以在筷波仪上观察，这就是振子链上机械波在阻抗突变点反射与折射时有趣的物理图像，如图7照片所示。

4 小结

本文对筷波仪振子链上的扭转振动波的传输过程进行了分析，得到了机械波振幅反射率、振幅折射率、反射波及折射波能流密度随波阻抗变化的关系式。在此基础上，详细分析了在高阻抗和低阻抗反射时此扭转振动波的反射和折射的规律。特别是在高阻抗反射条件下，上游低阻抗区段反射波和入射波的叠加等价于一列驻波和一列

图6 振子链上的波在高阻抗界面上的反射与折射

图7 振子链上的波在高阻抗界面上的反射与折射波形照片

正向行波的叠加，在驻波诸振子作简谐振动通过平衡位置的时刻，低阻抗区段正向行波像是在波阻抗突变点突然改变了它的波数而变成了等振幅折射行波。这一结果也通过实验演示了出来。