一种基于自适应双稳态随机共振的中介轴承故障诊断方法

彭敏玲

(江苏联合职业技术学院 淮安生物工程分院，江苏 淮安 223200)

中介轴承安装于高低压转子间，工作环境条件恶劣，温度高、转速高，故障发生风险高。[1]在以往围绕中介轴承故障案例的分析与研究中不难发现，其故障状态下的信号参数具有频率构成复杂、振动信号衰减严重以及信号传递路径长等一系列特点，故障特征的提取面临着比较大的难度。

1 双稳态随机共振系统

双稳态随机共振理论是指基于非线性系统环境，融合所采集周期信号以及噪音信号，增强微弱故障信号参数。[2]作为应用作为广泛的非线性系统之一，双稳态系统最典型特点即双稳态平衡关系。[3]在受到外力作用以及随机白噪声影响的情况下，双稳态系统可以用式(1)进行描述。

(1)

将用结构参数a，b所描述的非线性双稳态势函数代入双稳态系统中，同时定义系统输出为x，s(t)为外部输入信号作用力，Γ(t)为高斯白噪声，则可以将双稳态随机共振系统描述为：

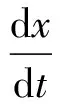
(2)

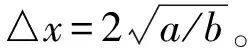
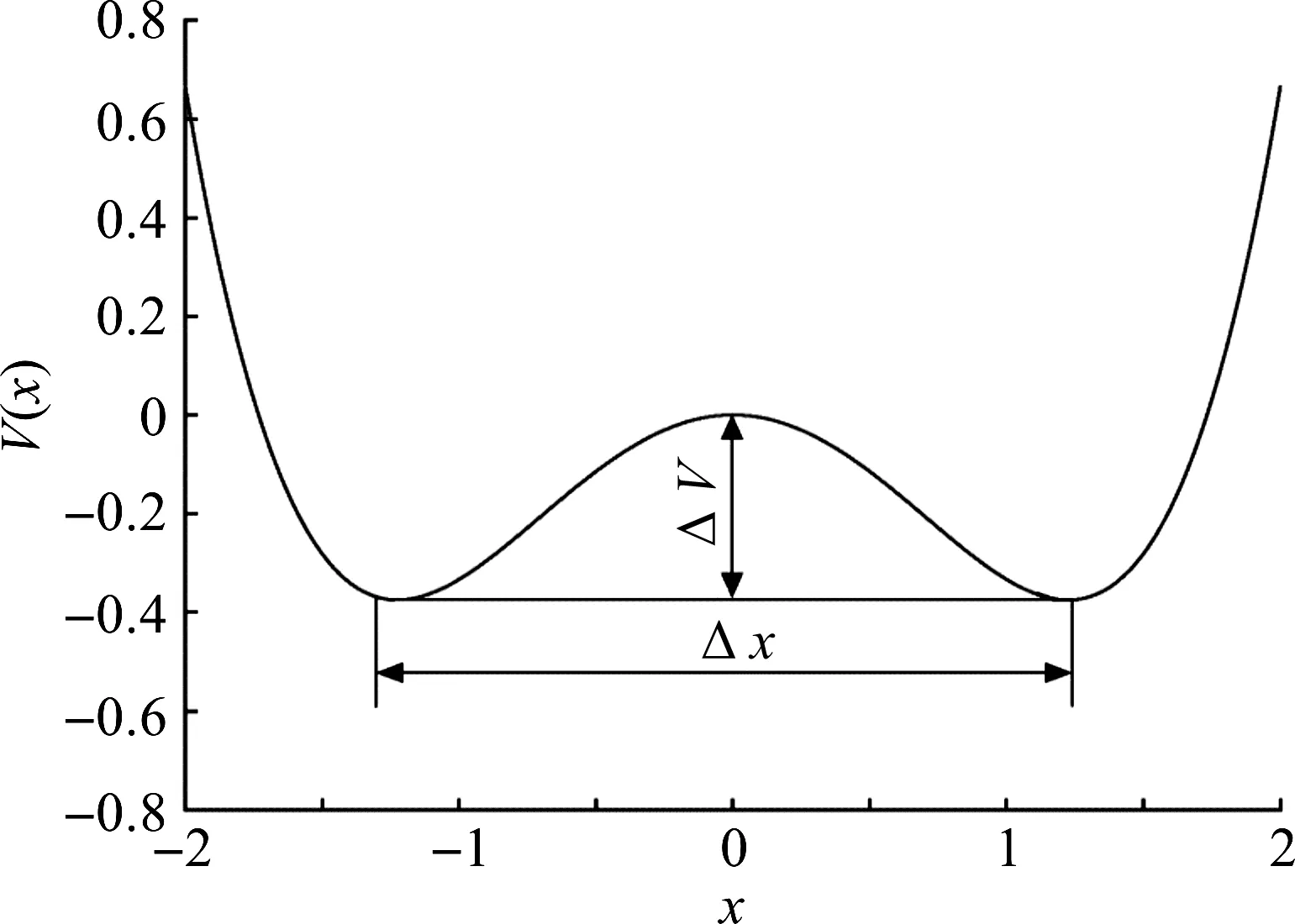
图1 势函数模型关系示意图

而在受到噪音干扰因素以及外部周期信号共同影响的情况下，可以适度调节a，b结构参数，并合理改善噪声强度水平，以外部信号所对应调制频率为依据，确保整个随机共振系统能够在两个势阱间进行动态切换，以同步周期信号与输出信号，通过这种方式提高小周期分量水平，增强微弱周期信号。

2 基于容忍遗传算法的自适应双稳态随机共振系统

2.1 容忍遗传算法

本算法可以在剔除任意体系经验的条件下编码参数，并搭载多条线路展开全局化搜索，实际应用中具有广泛性、灵活性的特点。将容忍遗传算法应用于双稳态随机共振系统结构参数的优化调整实践中，所生成的随机共振效应是非常理想且可靠的。[5]相对于随机共振系统中的结构参数a，b而言，应用容忍遗传算法对结构参数进行优化设置的基本流程(见图2)。

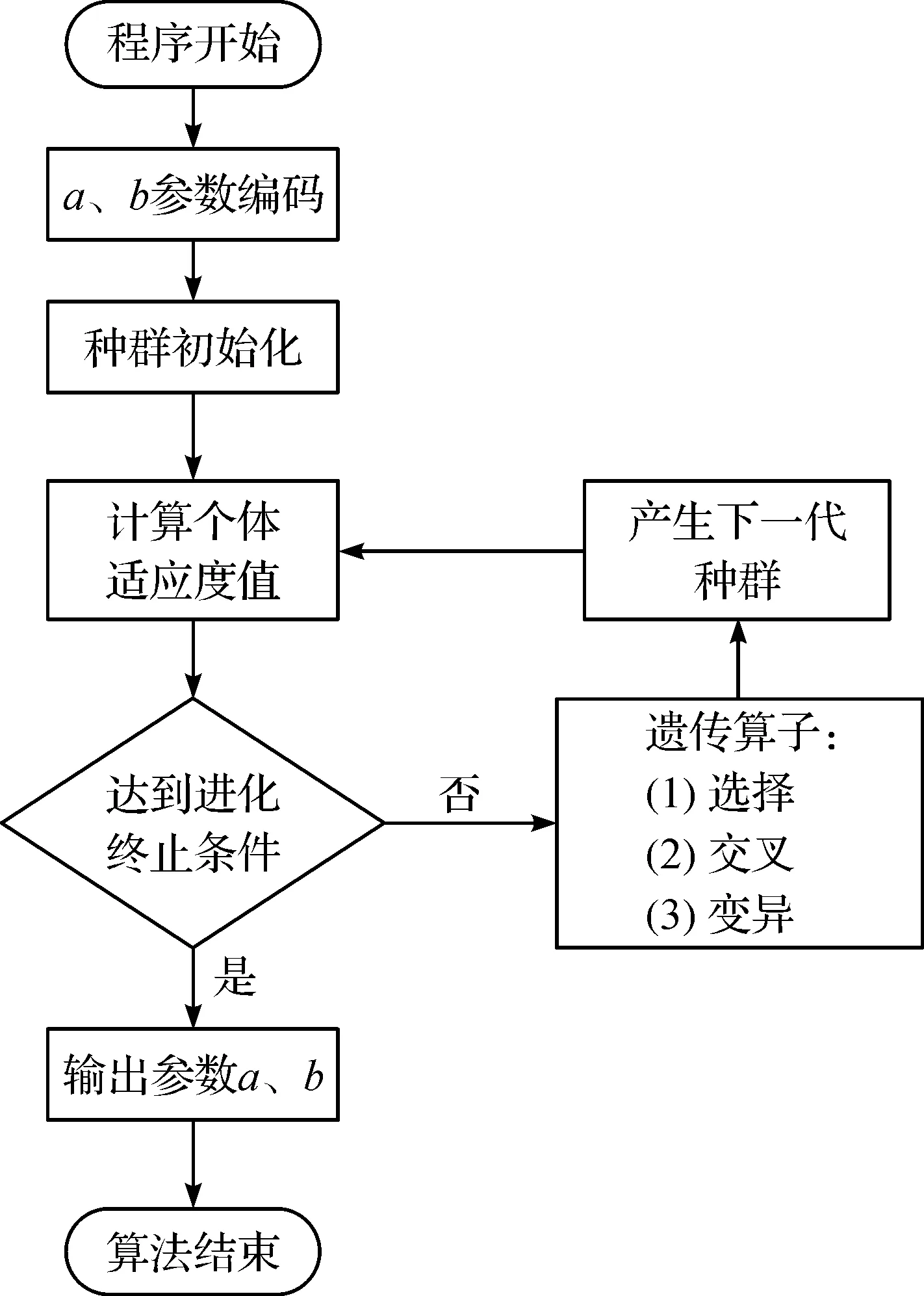
图2 基于容忍遗传算法的结构参数优化设置流程图

(1)初始化编码

整套系统算法采用初始化编码格式为二进制编码，在此基础之上设置结构参数a，b所对应求解精度，将其定义为ε，则有ε=0.001。

(2)容忍遗传算子

遗传算子包括选择、变异、以及交叉，是遗传算法运行中种群实现进化的关键所在。[6]假定在结构参数优化中引入容忍遗传度算法时，迭代代数被定义为N，每迭代所对应个体数量设置为M。因此，初始状态下迭代操作时系统结构参数相对应可行区间内通过随机方式抽取个体M进行选择性遗传操作，在N/2迭代遗传中将优势个体保留下来，以提高迭代收敛速度，保证容忍遗传算法的运行效率。后N/2迭代遗传则引入轮盘赌方式，提高随机性，预防局部最优解的问题。

在此基础之上假定交叉概率为Pc，则对随机选择结构参数a，b个体进行截断交叉处理(采用二进制位方式)，并生成全新个体，从而促进整套算法全局搜索能力的提升。因而，当假定交叉概率Pc对应上限为Pcu，对应下限为Pcl时，且两个交叉个体中较大适应度表示为fc，当前代最大适应度表示为fmax，当前代平均适应度表示为fmean，容忍适应度极限值表示为Ltfc，则可以将交叉概率按照式(3)表示。

(3)

假定容忍遗传算法过程中的变异概率为Pm，对于来源于自稳态随机共振系统中以随机方式筛选得到的a，b种群个体来说，可以基于二进制单位完成基因编码处理，这对于个体多样性的维持有非常重要的意义。为了能够使近似最优解最为理想，可在容忍遗传计算将具有自适应性的变异算子引入其中，在迭代处理基础之上确保系统具备局部最优解范畴的跳出能力，算法搜索深度水平得到保障。[7]假定变异概率所对应上限为Pmu，对应下限为Pml，变异个体适应度值表示为fm，容忍适应度极限值表示为Ltfm，则可以将变异概率按照式(4)表示。

(4)

建立在容忍度基础之上的自适应遗传算法实质上是在自适应算法过程中加入基于容忍限度的思想。借助于容忍度的方式处理分界函数分界点，在这种情形下，一串数据所对应波动速度无法借助于单一平均值加以反应，以分界点为依据所计算得到的遗传概率临界点处于较为绝对的状态，缺乏与生物遗传度计算结果的一致性与相似度。

(3)适应度函数评价

在容忍度概念下构建自适应遗传算法核心是形成一个利用个体适应值大小对个体优劣程度进行可靠评定的评估系统。为了能够促进系统信号增强能力的提升，可以在输出信噪比的辅助下形成基于适应度的函数关系，将输出信噪比定义为Gsnr，out，适应度函数定义为Fn(x)，则可以按照式(5)进行表示。

Fn(x)=Gsnr，out(a，b，x)

(5)

(4)终止条件

在个体持续性优化处理的过程中，以最优个体a，b对应迭代处理次数达到200代预设值的情况下，进化终止并输出a，b作为系统参数的最优解。

2.2 自适应双稳态随机共振系统

构建建立在容忍度遗传算法基础之上的自适应优化体系，算法基本运作流程(见图3)。[8]结合图3，自适应优化系统对故障状态信号进行采集，以信噪比为依据形成适应度函数关系，并引入负载均衡算法，优化设置整个随机共振系统中的关键结构参数，在此基础之上寻找最优参数构建随机共振系统并处理中介轴承故障信号，通过包络分析的方式提取与该故障相对应的特征频率参数，达到诊断故障类型的目的。

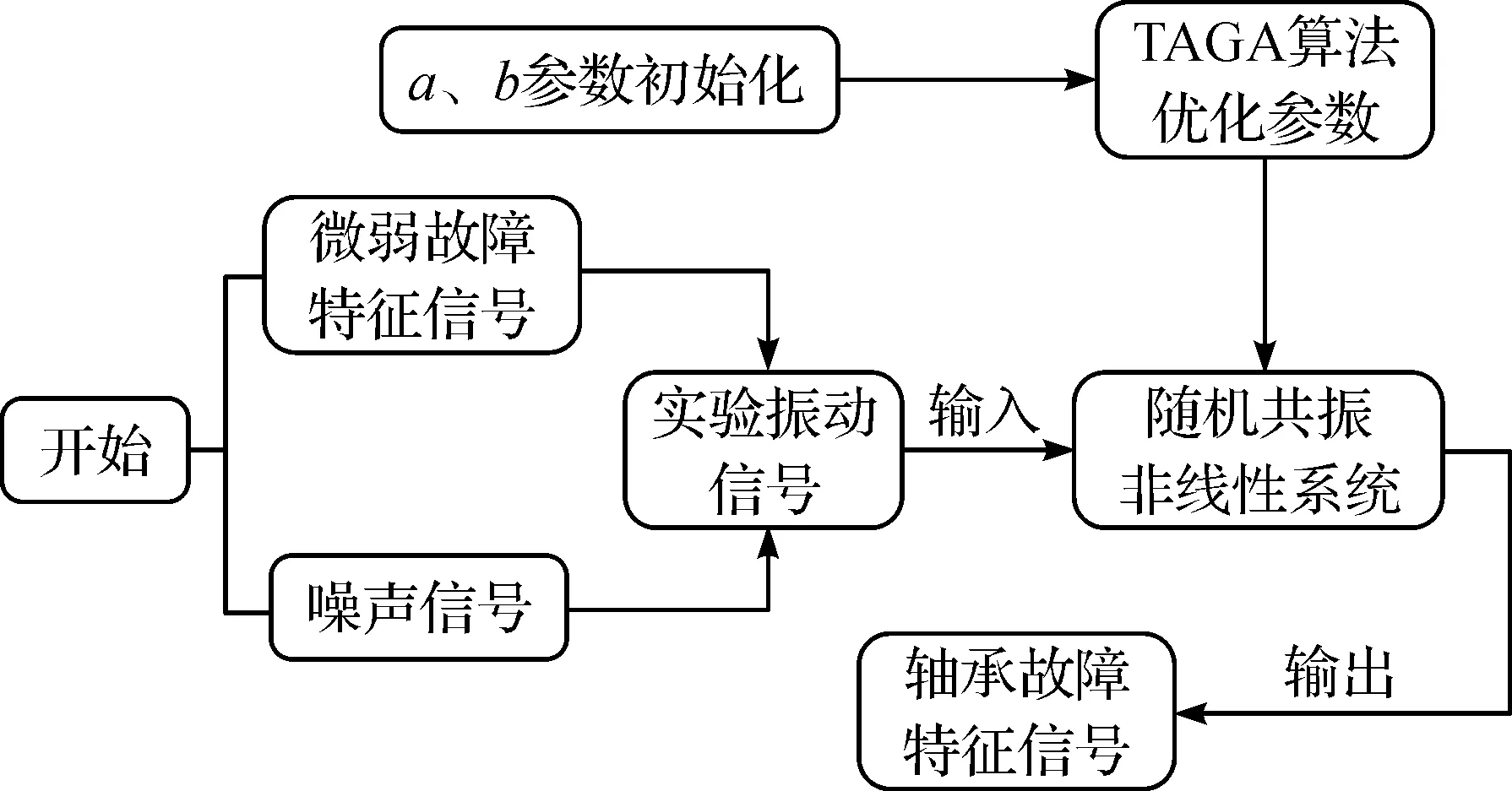
图3 基于容忍遗传算法的双稳态随机共振系统算法流程示意图

3 中介轴承故障诊断实验验证

为验证基于自适应双稳态随机共振系统进行中介轴承故障诊断的实用性与有效性，对搭建双转子试验台展开故障模拟实验，整套系统由转子、电机驱动、支撑、数据采集这几个模块所构成，采用线切割方法对轴承外圈制作表面缺陷，缺陷深度0.5 mm，宽度0.5 mm，纵向贯穿外圈表面。故障模拟实验过程中高低压转子沿反向旋转，外圈故障状态下高压转子转速为1 000.0 r/min，低压转子转速为600.0 r/min，故障信号采集时间为20.0 s，采样工作频率为16 384 Hz。[9]以下针对外圈故障应用自适应双稳态随机共振系统诊断效果进行验证。

分别采集高压转子转速为1 000.0 r/min，低压转子转速为600.0 r/min条件下的外圈故障振动信号，假定内圈转速为n1，外圈转速为n0，滚子直径为d，轴承滚子个数为Z，轴承节径为Dm，轴承压力角为α，则可根据下式计算得到外圈故障特征频率：

(6)

图4为经传感器装置对中介轴承外圈故障进行采集的信号示意图。结合故障信号可见，时域信号存在一定的冲击性成分表，但在其他部件振动噪音的同步作用下，故障波形上并没有表现出明显的周期性规律。故障信号能量集中分布在40.0～200.0 Hz区间内，低频范围内能量密度偏低，信号较弱，给故障特征频率的提取带来了一定难度。

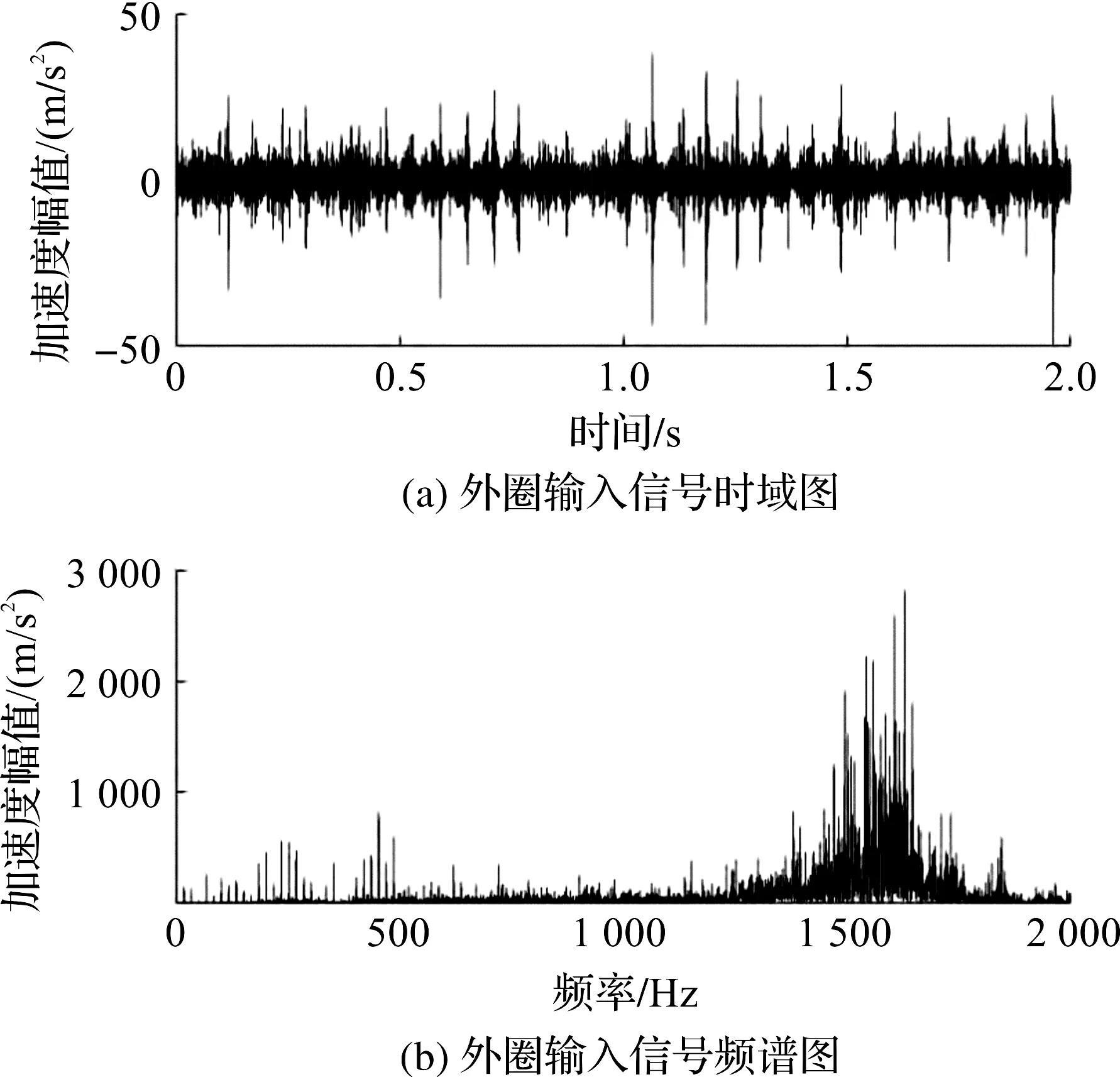
图4 传感器采集中介轴承外圈故障信号示意图

为解决这一问题，采用上文所提出的自适应双稳态随机共振系统对故障信号进行处理，处理结果(见图5)。

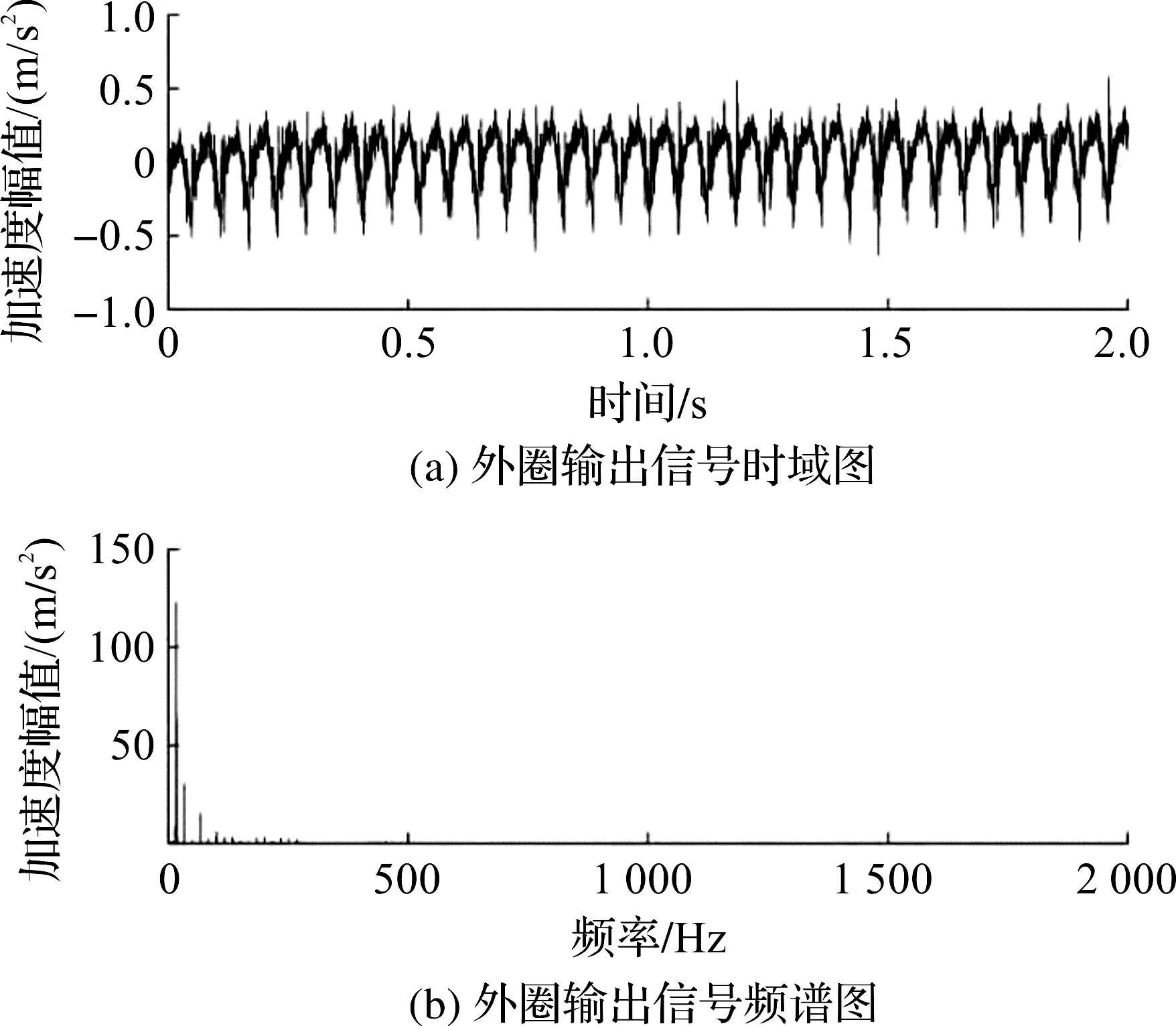
图5 自适应双稳态随机共振系统处理后外圈故障信号示意图

根据图5中的时域波形可见，经自适应双稳态随机共振系统处理后过滤了采集信号中的大量高频噪声，信号峰值波动整体趋向于稳定状态，在冲击信号上有较为明显的周期性规律，在400.0～2 000.0 Hz范围内，信号经处理后能量显著降低，低频范围内能量升高明显，主要原因是高频信号转移至低频信号，提升了低频范围内的能量强度，方便了后续对中介轴承故障频率特征的有效提取。

4 结 语

综上所述，文章提出了基于容忍算法的自适应双稳态随机共振系统算法，该算法可以对结构参数进行自适应优化处理，通过对算法的应用，能够有效抑制所采集中介轴承信号中噪音信号，增强周期性信号，使故障特征提取更加有效，为故障诊断奠定基础。