在流变效应影响下面板堆石坝应力变形分析

黄小华

(福建水利电力职业技术学院，福建 永安 366000)

混凝土面板堆石坝以其具有工期短、投资省、施工简便得到迅速发展。面板堆石坝目前最主要的技术难题是控制堆石体的变形，因为混凝土面板的防渗性能与堆石体的变形息息相关[1-2]。如果堆石体后期的变形过大将导致混凝土面板与堆石体脱空开裂进而影响到坝体的防渗性和安全性。在面板堆石坝以往的设计中，采用弹塑性本构模型计算结果往往与实测结果有较大差异，这是因为堆石料是具有弹性、塑性以及粘滞性的综合体，这类材料的变形不仅与材料所受的应力状态有关，而且还受到时间的影响，即堆石料具有流变特性。因此，在混凝土面板堆石坝的设计中，考虑堆石料流变特性的应力应变分析在理论和实践上都变得非常必要。

1 堆石料流变机理及影响因素

堆石料产生流变的最主要原因是颗粒的破碎和滑移。单从概念上分析，堆石流变应该与土体的流变机理相类似，但是由于堆石与土体的材质、颗粒大小以及粒间接触形式不同导致它们流变的发生机理也不同[3-4]。细粒土的流变机理是当孔隙水压力消散完成主固结后，土体骨架发生蠕变使土体发生缓慢的变形过程。以点或面接触为主要特征及颗粒空间排列无规则性的堆石排水自由，渗透系数很大，不存在主、次固结现象。堆石料的变形主要分为两个阶段，首先是外力变形阶段，堆石体在外力的振动碾压作用下，体积缩小，即堆石的主压缩阶段。由于外力做功时间很短，堆石难以形成蠕变。在这个阶段以脆性接触为主的堆石颗粒棱角因破碎导致颗粒之间相互滑移、填充，并随着外力做功的增加，堆石颗粒的破碎滑移填充也会迅速加快。但是由于颗粒填充不太密实也就为以后的流变创造了条件。其次是流变阶段，堆石颗粒在应力重分布的作用下使少量粗大颗粒棱角被破碎、细化，破碎的堆石颗粒产生滑移导致堆石料产生进一步的缓慢变形即流变。堆石流变的速率会随着颗粒充填空隙的速率而变化，起初速率比较快，后面变缓。除此之外，还与堆石的岩质，颗粒级配及应力水平等有关。显然，堆石的流变不会无限发展，在经历较长的时间后，堆石颗粒不在破碎，最后趋于静止。

2 堆石料流变模型

堆石料由于包含弹性变形、塑性变形和流变变形三个部分，且三种变形在时间上又相互交替作用。因此堆石料变形非常复杂。在前人的不断探索研究中总结出很多的流变经验模型，主要包括三参数流变模型、七参数流变模型、幂函数流变模型、双屈服面流变模型等。考虑到七参数流变模型理论成熟，模型参数计算简便，本文堆石料流变模型采用七参数指数衰减型流变模型[5-7]。李国英等[7]人通过对堆石料的试验结果建议对最终体积流变εvf和最终剪切流变γf采用关系式(1)与式(2)。

(1)

(2)

在Prandtl-Reuss假设下，应变率张量可由下式计算：

(3)

材料的体积变形速率和剪切变形速率分别为：

(4)

(5)

式中，εvf和γf分别为体积最终流变量和剪切最终流变量；εvt和γt为t时段已积累的体积流变和剪切流变。该模型中包含α、b、c、d、m1、m2、m3七个参数，故称之为七参数模型。

3 考虑流变效应的大坝应力变形分析

3.1 工程概况

仙游抽水蓄能电站上水库大坝为混凝土面板堆石坝，坝顶设计高程为746.6 m，坝顶上游设防浪墙，墙顶高程为748.8 m。该坝坝顶长度340.0 m，坝顶宽度8 m，趾板基础最低高程为674.0 m，最大坝高73.6 m。坝体上面面坡度为1 ∶1.4，下游面坡度为1 ∶1.8。坝体填筑材料分成主堆石区、下游堆石区、垫层区、特殊垫层区、过渡区、上游粉质粘土铺盖及石渣护面。垫层区及过渡区坡度均为1 ∶1.40，垫层区水平宽度为3.0 m，过渡区水平宽度为4.0 m。面板顶部高程743.6 m，顶部厚度为0.3 m，渐变至面板底部厚度为0.5 m。

该坝2009年4月开始施工导流，10月主体工程开工。面板混凝土于2011年10月开始浇筑，至2012年1月浇筑完成。2012年5月水库下闸蓄水。堆石坝典型断面图(见图1)。

图1 堆石坝典型断面

3.2 计算模型及参数

本文在三维有限元计算中，采用六面体八结点或退化的八结点等参数单元模型堆石料和混凝土面板。坝体划分为49个横断面，三维有限元网格结点总数为12 605，单元总数为11 487(见图2)，其中，混凝土面板单元475，堆石体10 254，接触面单元475，接缝单元283。堆石料的变形由瞬时变形和流变两部分组成，计算时瞬时变形采用沈珠江双屈服面模型[8]，流变采用七参数模型。材料参数参考同类工程取值(见表1)，在流变分析中，垫层和过渡层材料参数与主堆石材料参数一致(见表2)。

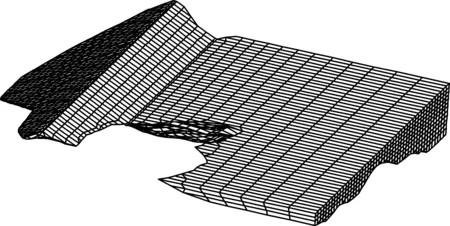
图2 坝体有限元网格划分图

表1 双屈服面模型计算参数

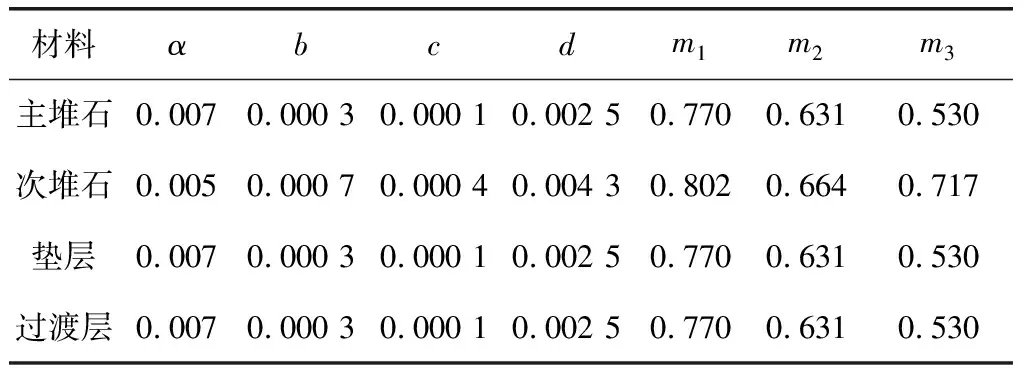
表2 流变模型参数

3.3 计算结果与分析

3.3.1 堆石流变对坝体应力变形的影响

经过三维有限元计算分析，水库蓄水运行两年时，不计流变效应和计入流变效应的面板堆石坝应力变形最大值计算结果(见表3)，蓄水期面板堆石坝典型断面计入流变后水平位移、垂直位移及大小主应力(见图3—6)。

表3 蓄水期面板堆石坝应力变形最大值表

由图3可以看出，在堆石体自重的作用下，水平位移在断面的分布上大致呈对称分布，即上部坡面向内收缩，下部坡面向外鼓出。由表3可以看出，当面板堆石坝蓄水运行两年时，不计流变效应前，堆石体向上游最大水平位移为5.83 cm，向下游最大水平位移为4.43 cm。当计入流变效应后，两者位移值分别增加了4.08 cm和1.89 cm,增幅分别达到70%和43%。由图4可以看出，在计入流变效应时，堆石体最大垂直位移为40.5 cm，约占坝高的0.55%，出现在河床断面坝轴线偏向下游约1/2坝高处，并从位移最大值处向四周逐渐减小。由表3可知，当计入流变效应后，该位移值增大11 cm,增幅达到37%。计算结果显示，计入堆石流变效应前后，堆石坝的变形规律大致相似，但是位移变形量均有所增加，可见，堆石流变对堆石体的变形有较大影响。

由图5—6可以看出，大小主应力线出现上台并与面板相交，且等值线大致与面板平行，最大值出现在河谷段坝基面附近。由表3可知，当不计入流变效应时，最大主应力值为1.16 MPa，最小主应力值为0.5 MPa。当计入流变效应时，最大主应力值为1.18 MPa，最小主应力值为0.55 MPa。可见，堆石体大小主应力在流变效应的影响下有所增大。

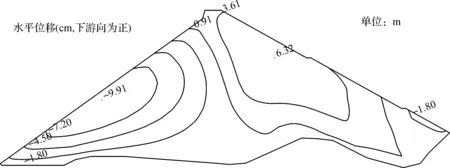
图3 坝体蓄水期水平位移等值线图(含流变)

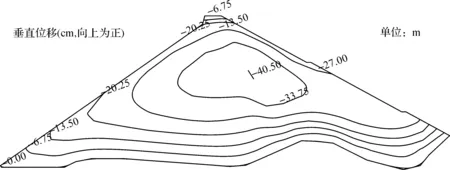
图4 坝体蓄水期垂直位移等值线图(含流变)

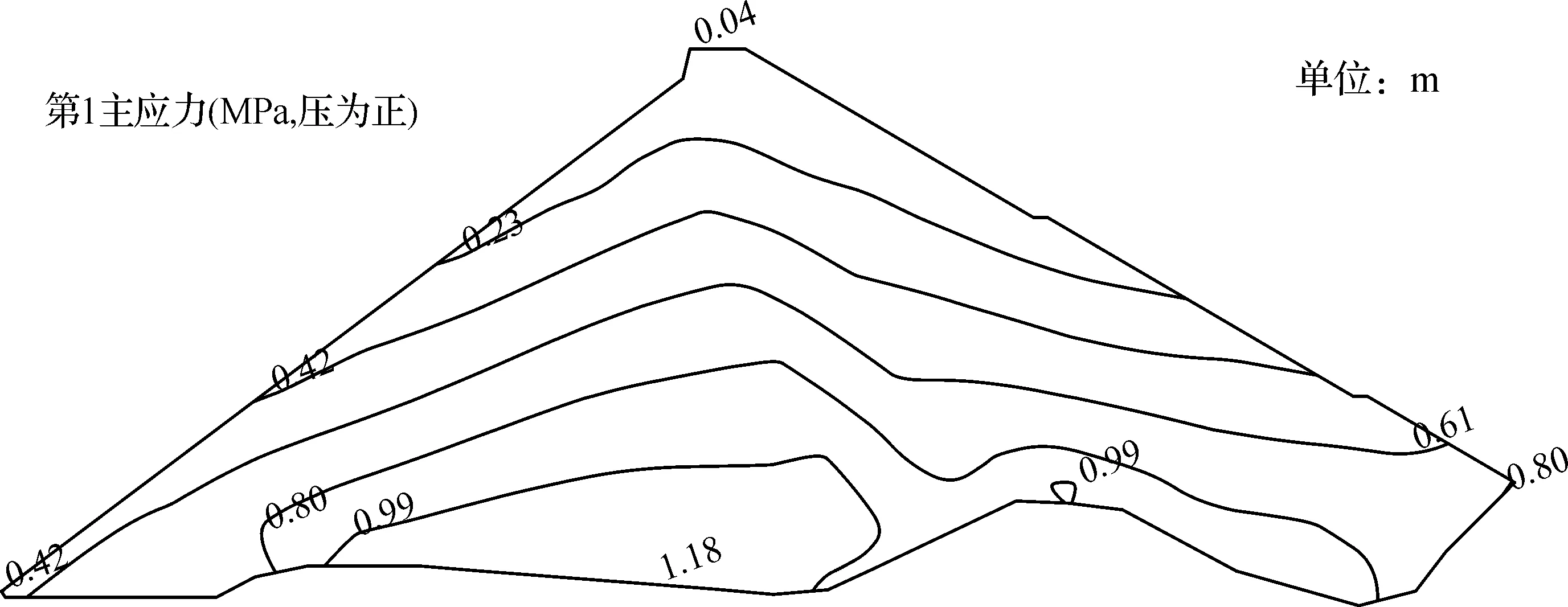
图5 坝体蓄水期第1主应力等值线图(含流变)

图6 坝体蓄水期第3主应力等值线图(含流变)

3.3.2 堆石流变对面板应力变形的影响

不计流变效应与计入流变效应的堆石坝面板应力变形计算结果(见表4)。从表中可以看出，在堆石流变的影响下，面板坝轴向方向位移均有所增大。水库蓄水后，在坝体自重和上游水压力的作用下，面板呈现一种向下凹的曲面，最大挠度发生在面板中部偏下位置。考虑流变情况下，最大挠度值为10.8 cm，较不考虑流变效应影响增大了50%。在堆石流变的影响下，面板顺坡向拉压应力和坝轴向拉压应力均有不同程度增大，分布规律基本不变。可见，堆石流变对面板的应力变形影响较为明显，使面板的应力变形进一步增大。

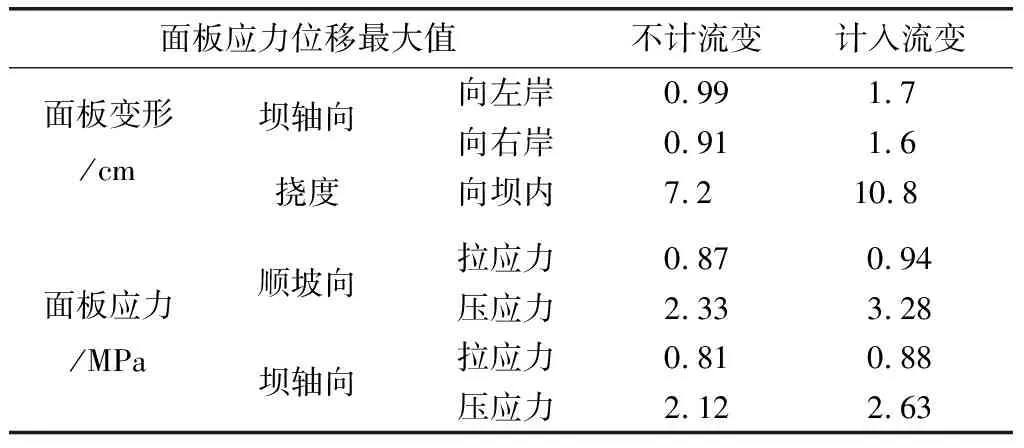
表4 面板应力变形最大值表

4 结 语

通过堆石流变机理及流变模型分析，结合某面板堆石坝是否考虑堆石流变效应影响两种方案的应力变形计算结果，笔者认为，堆石料的流变效应使堆石坝坝体和面板的应力变形均有所增大。因此，面板堆石坝应力变形分析中考虑流变效应更能真实的反映面板堆石坝应力变形特性，减少面板被压碎和拉裂的风险。