带宽化扰动观测复合滑模的闭链机构协调控制

姚苏华 ,高国琴 ,高志强

(1.江苏大学电气信息工程学院,江苏镇江 212013;2.克利夫兰州立大学电机工程与计算机科学系,俄亥俄州克里夫兰市44115)

1 引言

目前汽车电泳涂装输送设备大多采用悬臂梁结构,为克服悬臂梁结构承载能力不足的缺点,本课题组将并联机构引入输送机,发明了一种并联汽车电泳涂装输送机[1–2].输送机包含两个完全对称的并联机构,并联机构末端通过一对转动副与一根连接杆的两端连接,车体悬架固定在具有一个转动自由度的连接杆上.输送机构作为闭链机构,机构支链公共端连接点处的弹性刚度具有一定的极限,主动关节不协调易引发支链接触处受力超出刚度允许范围,导致塑性形变,轻则带来机构磨损,重则造成闭链解构,因此,从控制上保证输送机构每边及两边主动关节位置协调性十分关键;而实际系统受到负载变化(如车型调整)、模型不准确、关节摩擦及流体阻力等内外扰动综合影响,而且上述扰动对各个主动关节位置输出影响也不具有一致性,因此,在非一致的扰动作用下,如何通过控制实施保证主动关节位置协调性,是协调控制的核心难点.

解决协调控制问题,目前主要有同等控制[3]、主从控制[4]、虚拟主轴控制[5]、偏差耦合控制[6]及交叉耦合控制[7]等方案.其中交叉耦合控制由Koren Y首次提出[8],已被用于解决多轴系统[9–10]、移动机器人[11]、多机器人[12–13]、多关节灵巧手[14]及并联机构[15–17]等协调控制问题.而针对闭链机构,文献[15–16]将交叉耦合控制与比例微分(proportional derivative,PD)控制或自适应控制结合;文献[17]结合相邻交叉耦合提出同步高阶PD控制等等,综合来看,交叉耦合控制没有明确划分不确定问题和协调控制问题的界限,这说明协调控制问题本身只是一类特殊的不确定问题,其特殊性在于:在扰动对输出影响不一致的情况下,通过控制实现输出稳定一致.

解决不确定问题一般使用跟踪误差反馈,而交叉耦合控制解决协调控制这种特殊的不确定问题也可以使用耦合误差反馈,如文献[14,17].在文献[10]所定义的耦合误差中,跟踪误差与同步误差的阶是一致的,因此耦合误差可以表示为一个非奇异矩阵与跟踪误差向量的左积.控制直接利用耦合误差与跟踪误差这一线性关系,可以通过线性变换将建模空间中的协调控制问题转化(描述)为耦合空间中的不确定(抗扰)问题.由此可见,协调控制要解决正是另一空间的不确定问题.

解决不确定问题的方法很多,滑模控制就是其中的一种.作为一类特殊的非线性控制,滑模控制具有响应速度快、鲁棒性好、实现简单的优点,但也存在抖振问题.文献[18]提出将滑模控制与非线性扰动观测器(nonlinear disturbance observer,NDOB)结合,通过扰动观测器减少不确定上界,从而减轻滑模控制的抖振;文献[19]结合文献[18],并与交叉耦合控制结合,也在一定程度上解决了并联机构主动关节协调控制问题.然而,非线性扰动观测器(NDOB)的主要功能是补偿标称模型误差和外部扰动,设计需要植入标称逆模型,当标称模型较为复杂时,会降低控制计算的实时性.为简化扰动观测器设计,本文提出一种新型扰动观测器,它借用扩张状态观测(extended state observer,ESO)[20]的计算结构,并使用估计误差的比例、积分、微分(P,I,D)估计总扰动.它与滑模控制复合,不仅可以消除滑模控制的抖振,降低滑模控制对趋近率的选择要求;更重要的还在于闭环系统动态统一设计的实现,与带宽参数化的结合,又能有效地解决控制参数的整定问题.

至此,本文后续安排如下:首先给出闭链机构在建模空间和耦合空间描述;在耦合空间中提出扰动观测器复合滑模的控制方法;给出稳定性证明后提出带宽参数化整定方法;在仿真和实验的基础上给出研究结论.

2 协调控制问题在不同空间中的描述

2.1 建模空间描述

电泳涂装输送机构结构图如图1所示,文献[21]通过拉格朗日法建立操作空间的动力学模型,然后将操作空间的动力学映射到关节空间,得到关节动力学模型

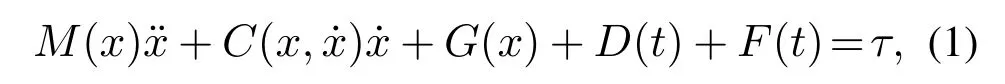
其中:D(t)为摩擦力项,D(t)=Fcsgnx+BcFc为库仑摩擦力矩阵,Bc为粘度系数矩阵,输出向量为x=[x1x2x3x4ϕ1ϕ2]T,xi,i=1,2,3,4分别为4个平移关节在位移,ϕj,j=1,2分别为两个翻转关节逆时针转动角度,F(t)为外界干扰项,包括空气及槽液阻力等.

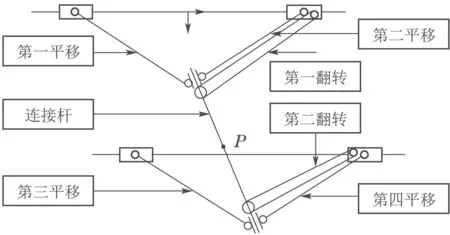
图1 电泳涂装输送机构结构图Fig.1 Structural diagram of electro-coating conveyor

注1上述动力学模型建立时的隐性假设为支链在接触点处的刚度为无穷大.超出刚度允许的高阶动态无法通过模型体现,一旦主动关节位置不协调,依据标称模型设计的低阶控制器因难以抑制高阶快变未建模动态影响,会引起系统不稳定.

设6个主动关节(4个平移关节和2个旋转关节)的位置跟踪误差为

式中:xid(t),xi(t)分别为第i个平移关节在t时刻的期望位置和实际位置;ϕjd(t),ϕj(t)分别为第j个旋转关节在t时刻的期望位置和实际位置.

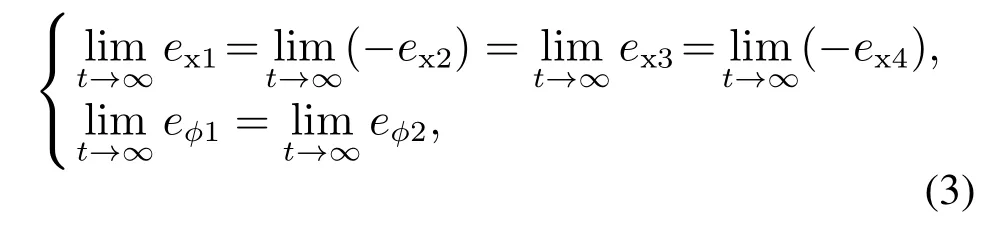
在建模空间中,协调控制问题可以描述为通过控制实现目标即实现4个平移关节和2个旋转关节的跟踪误差分别一致收敛.

2.2 耦合空间描述

根据式(3)的协调控制目标,根据文献[21],可将4个平移关节和2个旋转关节视为2组智能体,每组智能体之间可以相互通信,因此,首先画出两组智能体的强连通图,如图2所示.

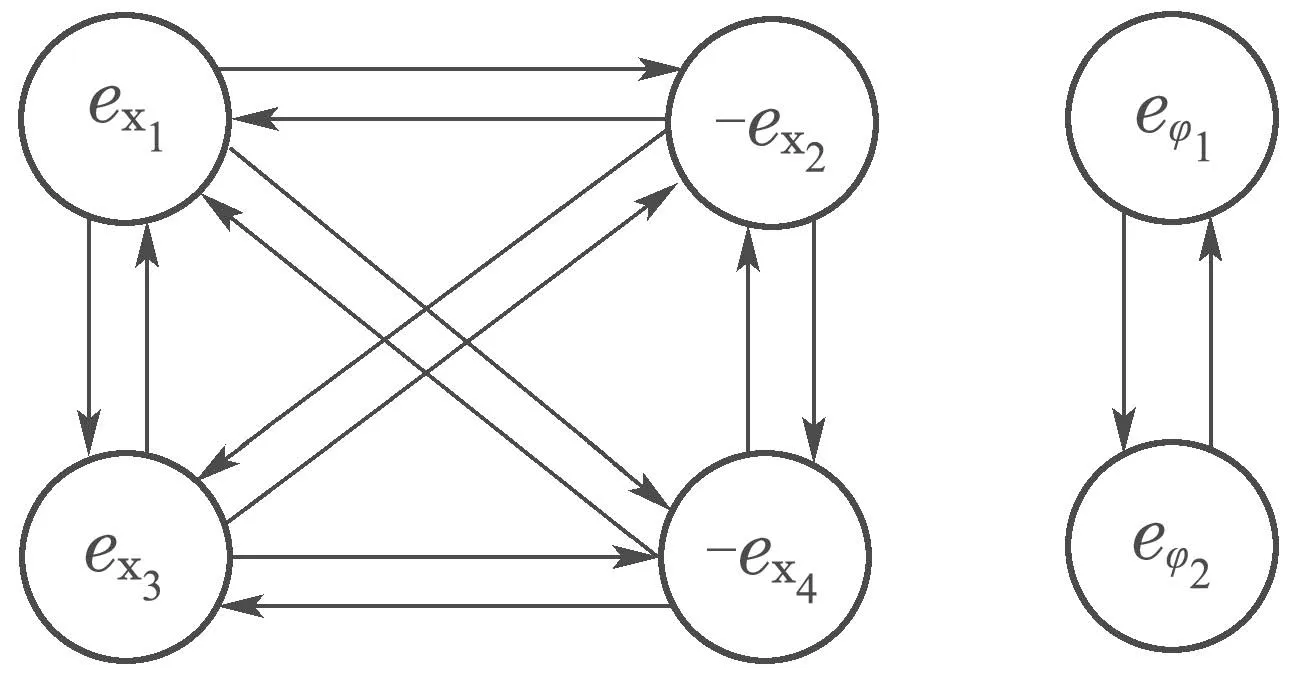
图2 平移关节及旋转关节的连通图Fig.2 Connected graphs of translational and rotational joints

图2对应的拉普拉斯矩阵(Laplacian matrix)为

定义同步误差向量

其中:e=[ex1ex2ex3ex4eϕ1eϕ2]T,同步传递矩阵T=diag{Tx,Tϕ}.考虑式(3)中的ex2和ex4取负号,为保证

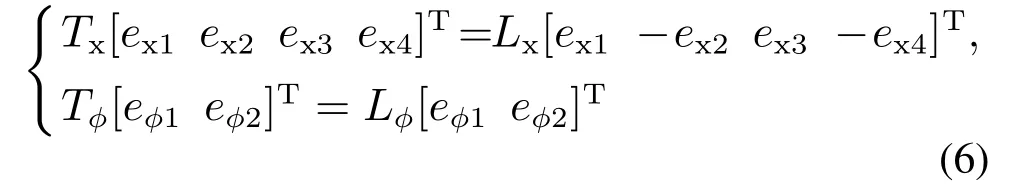
成立,应该满足

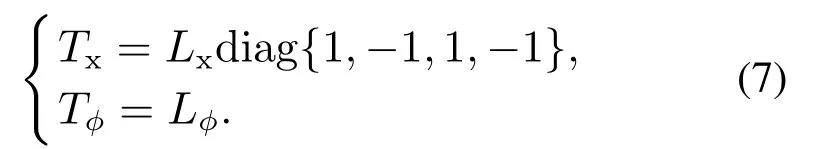
定义耦合误差[14]

结合式(5)得

其中:kε=diag{kε1I4,kε2I2},kε1,kε2均为正的常数,I表示单位矩阵.

定义耦合传递矩阵

由式(10)知Ts可逆,耦合误差与跟踪误差满足

线性关系.

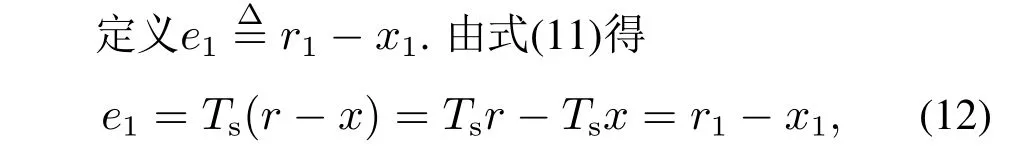
其中:r1=Tsr,x1=Tsx.

由式(1)得

将式(14)代入式(13)后两边左乘Ts得

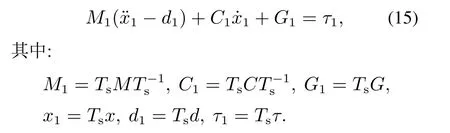
利用耦合传递矩阵Ts,主动关节协调控制问题就转化为解决耦合空间动态系统(15)的不确定问题,协调控制的目标就转换为:通过设计τ1,使e1→0.

3 扰动观测复合滑模控制

针对耦合空间的不确定问题,首先将式(15)转化为积分串联型

设计扰动观测器

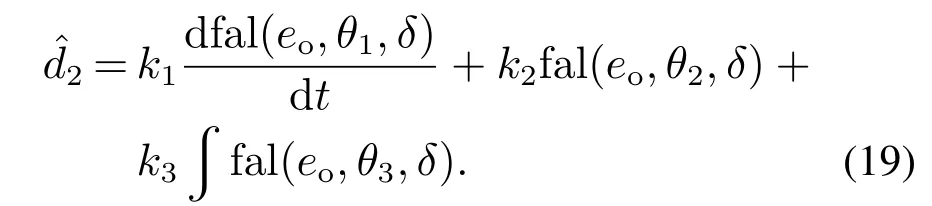
估计d2,使→d2.与文献[15]采用观测误差积分估计总扰动不同,式(19)使用观测误差的非线性PID估计总扰动,扰动观测器增益与ESO中3个反馈增益一致,对扰动信号的要求为:扰动及其扰动信号的导数有界[23].将代入式(17)得

针对式(21),定义滑模面

然后设计滑模控制律

其中ks=diag{ks1,…,ks6}.综上可知,扰动观测复合滑模控制律为

其中η0.

4 稳定性证明

扩张状态观测器关于z1的状态方程等价于非线性微分方程

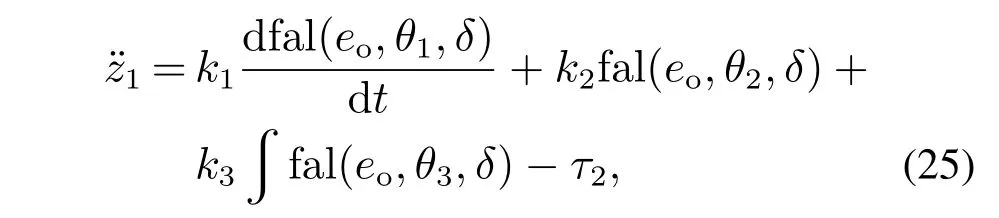
其中eo=e1−z1.将式(25)代入式(19)得

联立式(22)–(23)得

联立式(17)(23)得

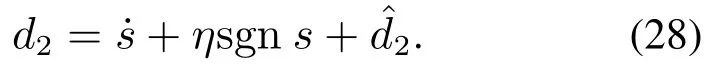
联立式(19)(27)–(28)得

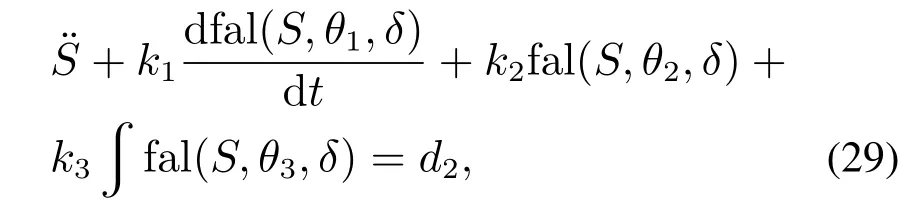
其中:

式(29)等价于

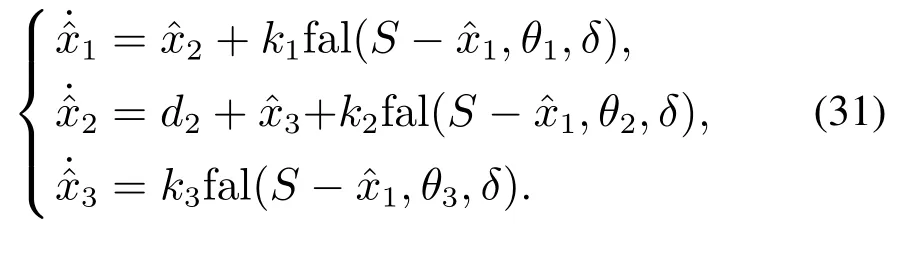
比较式(29)(33)得

注2滑模控制的切换增益ηO,放宽了滑模控制切换增益一般要求ηsup|d|的条件,同时,切换项两重积分的平滑作用是滑模抖振得以消除的根本原因.

注3式(30)揭示了扰动观测复合滑模控制的自抗扰本质[22].

5 带宽参数化整定

解决滑模控制参数ks和扰动观测器参数ki(i=1,…,3)的整定问题,是获得高性能协调控制性能关键.由于本文新型扰动观测器使用了fal型函数,fal作为分段函数,其第1段是线性的,第2段是非线性分数指数幂函数(使用大误差小增益原理引入的类饱和保护行为[23],以防止系统超出执行限制).在平衡点附近,扰动观测器通常工作在第一段(线性区).由式(29)可知,系统闭环特征方程为

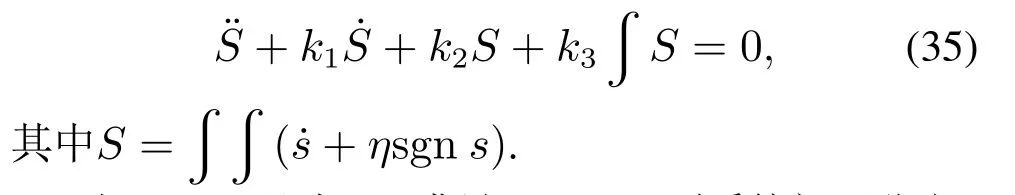
当η0,且式(35)满足Hurwitz,则系统闭环稳定.

为解决参数整定问题,不妨先设η=0,将式(22)代入式(35)并化简得

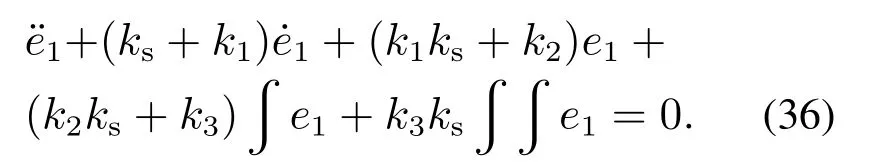
由式(36)知系统各个通道的闭环特征多项式均为

注4为区分式(22)变量,需要强调式(37)中的s是拉普拉斯算子.

结合带宽参数化[24]得

其中ωc,ωo分别为滑模控制器参数和扰动观测器的带宽.

求解式(38)得

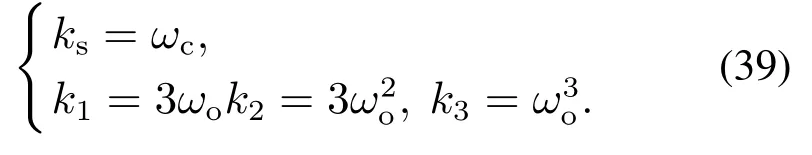
注5滑模控制器参数ks=ωc意味滑模面的增益参数具有带宽的物理意义,这也说明:在实际系统中使用滑模控制时,滑模面的设计应尊重有限带宽[25]这一根本系统限制.

当η >0,等速趋近律滑模切换项迫使状态趋向滑模面的趋近速率保持恒定,其代价在于控制量的幅值随之增加.在实际系统中控制量一般受饱和约束,因此满足η 0是实际系统实现稳定运行的必要条件.

6 仿真及实验

在MATLAB/Simulink环境下进行系统仿真,步长取0.001 s,离散化采用ode1,仿真时间为16 s;为方便比较,与文献[16]所设置的干扰保持一致,其中粘性系数矩阵、库伦摩擦力矩阵、外部干扰及建模误差分别取

将式(39)代入式(24),并取控制参数

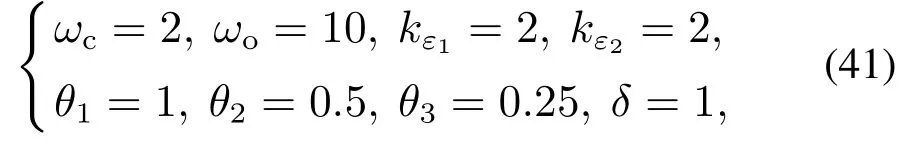
式(41)中θi(i=1,2,3)取值根据文献[20]直接得到,而δ的选择在实际应用中应根据执行器饱和限制条件取适当的值,本文仿真取δ=1.

选不同的η,检验系统的稳定性和滑模抖振情况.由于任意关节控制量输出曲线特征相似,为便于描述,本文仅给出平移关节1在t∈[0,8]取不同η时的控制量曲线.为进一步评价系统末端执行精度和主动关节同步精度,选择跟踪误差的均方根误差TRSME和同步误差的均方根误差SRSME分别用于评价跟踪和同步性能[17].

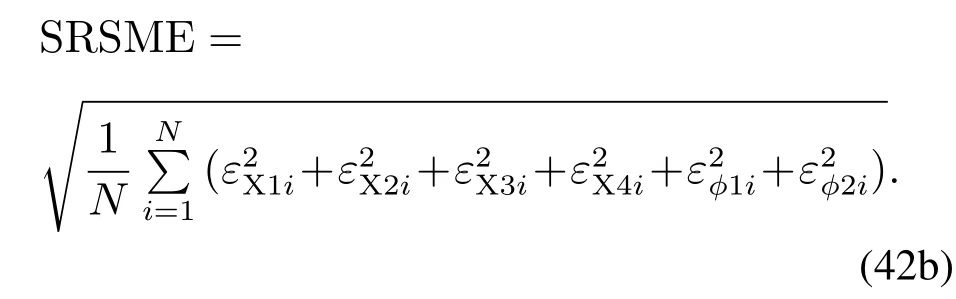
如图3所示,取η0时系统是稳定的,控制量幅值随η增大而增大,控制量平滑性好,控制量曲线中无明显的云状抖振区域.

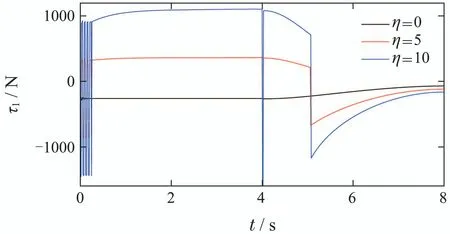
图3 平移关节1的控制量曲线Fig.3 Control curve of the first translational joint

表1列出η=0,5,10对应两个指标的仿真数据,η=0时,跟踪精度最高,随着η的提高,跟踪精度有所下降,但同步性能几乎不变,这说明新型扰动观测器复合滑模的方案可以很好解决闭链机构主动关节位置协调控制问题,与文献[19]选择传统的非线性扰动观测器结合双幂次趋近律的滑模控制的仿真结果对比后发现,不仅两项指标均获得明显提升,而且参数整定也更加简便.

表1 同步与跟踪性能指标Table 1 Synchronization &tracking performance indexes

结合图1和表1可以看出,在同等条件下,当滑模切换增益为零时,系统几乎以最小的能量代价获得了最佳的性能.这一方面说明了扰动估计器具有优越的扰动估计能力;而从另一方面来看,切换控制量的引入由于增加了扰动估计器的估计负担,因而切换的存在并不一定有利于性能的提升.

为了验证本文算法的有效性,在电泳输送样机平台上进行了实验,结合带宽参数化法整定,实验获得的主动关节跟踪误差曲线如图4所示,实验取η=0的情形.在图4中,前4张图显示的是4个主动平移关节的跟踪误差,最后两张图显示的是翻转关节的跟踪误差.平移关节和反转关节跟踪精度等级分别达到10−3m与10−2rad.4个平移关节跟踪误差曲线除粗细存在细微差别之外(关节传感器测量噪声不一致性是造成跟踪误差曲线在粗细有所差别的主要原因),误差曲线的形状基本保持一致,由此可见主动关节的协调控制性能较好.

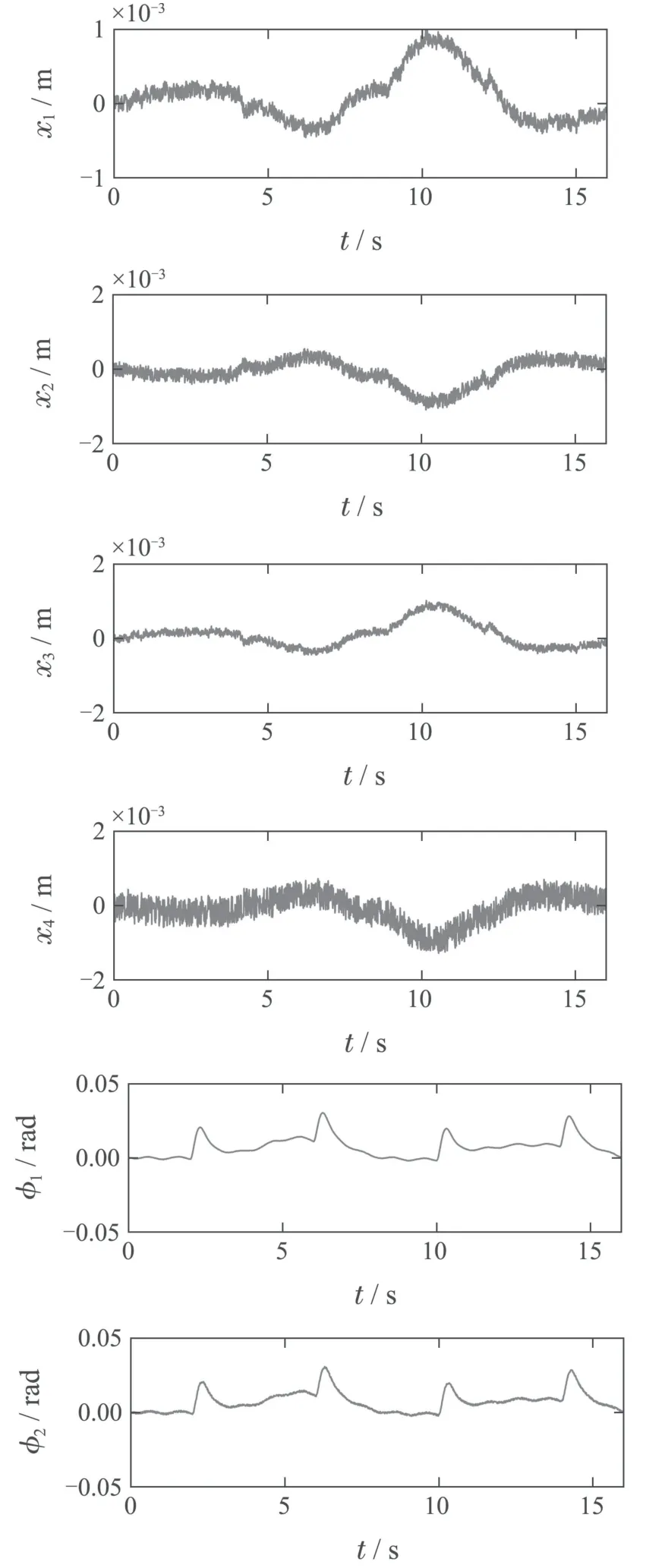
图4 6个主动关节跟踪误差Fig.4 Tracking errors of six active joints

7 结论

本文根据闭链机构特点,利用耦合误差与跟踪误差间的线性关系,将闭链机构协调控制问题描述为耦合空间中不确定问题,并在耦合空间中设计了带宽化扰动观测复合滑模的控制算法.本文主要工作如下:

1)提出了一种新型非线性扰动观测器,它保留非线性扩张状态观测器(NESO)的计算结构,并使用观测误差的P,I,D估计扰动;

2)结合稳定性证明,研究扰动观测复合滑模的闭环系统动态特征;

3)结合带宽参数化法解决参数整定问题.

仿真和实验表明,扰动观测复合滑模的控制方案不但可以有效解决闭链机构的协调控制问题,还具有参数整定容易的优点,因而还具有较高的工程应用价值.

扰动观测复合滑模、PID、自抗扰控制都具有状态扩张能力,直接表现为对系统升阶.系统的抗干扰能力强弱与控制对系统升阶次数之间是否存在某种必然联系,这是本文下一步要讨论的问题.