共享近邻紧密度的增量式谱聚类算法*

赵萌萌，王士同

1.江南大学 数字媒体学院，江苏 无锡214122

2.江南大学 江苏省媒体设计与软件技术重点实验室，江苏 无锡214122

1 引言

聚类分析是研究分类问题的一种统计分析方法，同时也是机器学习、数据挖掘的一种重要算法，其重要性在文本挖掘[1]、图像处理[2]等各个领域都得到了广泛认可。聚类算法旨在按照一定的标准将数据对象划分进不同的簇群内，使得在同一簇群内的相似度尽量高，不同簇群间的相似度尽量低[3]。近年来，谱聚类算法[4-6]已变为最受欢迎的聚类算法之一，谱聚类算法对于用相似矩阵的特征向量去揭示数据的簇群结构有一个很好的使用，在处理不同大小、不同形状的聚类时有很好的效果[7-9]。然而，传统的谱聚类算法不能揭示出一些复杂数据集的真正簇群，特别是未被完全分离的数据集。SC-SNN（spectral clustering based on closeness of shared nearest neighbors）算法[10-11]通过考虑共享近邻的紧密度来测量相似度，而非距离度量。因此SC-SNN 能够探索出两个数据点之间的潜在相似性，且对未能完全分离的数据集具有很好的健壮性。此外，它们在凝结的聚类算法和高维度的数据集的聚类方法中也能成功应用[12-14]。

虽然相对于其他聚类算法来说，SC-SNN 提升了未完全分离的数据集的分类质量，但它也有许多不足。由于SC-SNN 的计算时间复杂度和空间复杂度较高，当处理大规模和高维数据时，其时间开销较大，代价太昂贵，算法有可能会因为系统内存不足的原因而失效。而早在1990 年，Can 教授等就提出了增量式聚类算法[15]，以此来解决聚类时间复杂度较高，系统内存不足导致的算法失效等问题。所谓增量式聚类是指利用前期数据所获得的聚类结果对新增数据进行分批或逐次进行聚类的过程[16-17]。此种方法对于解决重复聚类造成的资源浪费，提高聚类算法的性能等问题有着十分重要的意义。关于增量式的谱聚类算法，目前有许多学者已有研究，如文献[18-19]等对研究此种算法提供了许多帮助。基于此种思想，本文提出了一种新的算法ISC-SNN（incremental spectral clustering based on closeness of shared nearest neighbors）来解决SC-SNN 算法所存在的问题，即将较大的数据集（适用于SC-SNN 算法，但由SC-SNN算法无法顺利、高效运行的数据集）随机均分为若干子集，第一个子集使用SC-SNN 算法，得出一个聚类结果，随后的子数据集以前一个子数据集及其聚类结果为训练集，结合SC-SNN 算法和KNN（K-nearest neighbor）算法得出聚类结果。改进后的ISC-SNN 算法既能减少聚类时间，提高聚类精度，也能有效解决因内存不足所造成的算法无法执行的情况。而且在实际的数据库中，数据量往往是不断增加的，使用增量式聚类算法，在面对新增的数据时，只需在原有数据库的基础上，进行一些由于新增的数据所引起的更新，不需要修改大规模数据，这将会节省很大的工作量。

2 相关算法

2.1 Normalized Cuts

谱聚类算法是基于谱图理论的，它能在任意形状的样本集上聚类且收敛于全局最优解，其本质是将聚类问题转化为图的划分问题。专家们基于Ratio cut[20]、Minimum Cuts[21]、Normalized Cuts[22]等 划分标准提出了不同的聚类方法，而本文算法是基于Normalized Cuts 提出的。Normalized Cuts 是由Shi和Malik 提出的一种无监督图像分割技术，它将图像分割问题转化为了图的划分问题。Normalized Cuts 既能满足类间的相似度最小，又能满足类内的相似度最大。而基于Normalized Cuts 的谱聚类算法的目标函数为：

其中，Laplacian 矩阵L=D-1/2SD-1/2，W是图G=(V,E)中各顶点的相似矩阵，D=diag(d1,d2,…,dn)称为W的度矩阵，di=∑jw(i,j)表示从点xi到其他点的连接度。

2.2 SC-SNN 算法

在Rd中给出具有n个数据点的数据集X={x1,x2,…,xn}，聚类算法将数据集划分为K个不相交的集合，每个集合称为一个簇。

（1）构造定向KNN 图

在定向KNN 图中，如果xj是xi的K最近邻之一，则xi到xj组成一条边。xj是xi的直接继承者，标记为xi→xj。此外，xi↔xj为xi与xj互为最近邻。

（2）建立共享近邻

在定向KNN 图中，Ni为xi的最近邻的集合。在xi和xj之间共享最近邻的集合为Ni⋂Nj。

成对相似性Sij是基于集合Ni⋂Nj进行测量的。通常Ni不包括xi这一点，故Ni⋂Nj不包括xi和xj两点。点xi和xj之间共享最近邻的集合Ni⋂Nj被定义为：

（3）度量成对相似性

为了测量成对相似性Sij，首先根据它们点xi和xj的距离去权重在Ni⋂Nj里的共享最近邻。用wij表示共享最近邻的权重。xr是Ni⋂Nj里的一个共享最近邻。假设xr是xi的第ithr个最近邻，是xj的第个最近邻。在定向KNN 图中，共享最近邻的权重wij依下式计算：

根据统计分析得知，Sij∈[0,1]。成对相似性Sij依据下列公式计算：

（4）计算Laplacian 矩阵

其中，S是图G=(V,E) 中各顶点的相似矩阵；D=diag(d1,d2,…,dn)称为S的度矩阵，di=∑jS(i,j)表示从点xi到其他点的连接度。

SC-SNN 算法的具体步骤如下：

输入：n个数据点，聚类簇数K，近邻数k。

输出：输入数据的簇标记。

步骤1构造定向的KNN 图，找出共享最近邻。

步骤2测量成对相似性，构造相似性矩阵S。

步骤3基于相似性矩阵S，计算归一化拉普拉斯算子矩阵L。

步骤4计算L的K最大特征向量。

步骤5以L的K最大特征向量为基础，将数据点分为K簇。

此算法在计算相似度矩阵，求特征向量时，消耗多项式时间，不难想象，随着数据量的不断增加，矩阵维度慢慢增大，时间消耗将逐渐变得不可接受。因此，将提出一种新的基于共享近邻紧密度的增量式谱聚类。

3 基于共享近邻紧密度的增量式谱聚类

3.1 ISC-SNN 算法

本节中将介绍ISC-SNN 算法。对于ISC-SNN 算法，重点放在对聚类的精确度以及时间的优化上。本文给出的处理方法为：先将较大的数据集分解为若干子集，然后逐步求解小数据集。这种方式主要具有有利的计算性质和实现简单等优点。下面给出其主要设计思想：

在Rd中给出具有n个数据点的数据集X={x1,x2,…,xn}，将其随机划分为T个大小基本相等的数据集DS1,DS2,…,DST。

首先，对于初始数据集DS1，使用算法SC-SNN得到数据集的聚类结果，构建训练集。由于聚类方法SC-SNN 是无监督方法，没有利用类别标签属性，在对数据集进行聚类时，如果对于某个数据集，初始的聚类算法分簇错误，就会造成某个聚簇中包含有不同实际类别的数据。为了解决此问题，在本文算法中，会在SC-SNN 算法的基础上加入KNN 算法，KNN 算法可以利用已测试数据集中包含的类别信息得出自身的类标签矩阵，使之与SC-SNN 算法得到的特征矩阵结合构成平衡项，这样就可以降低发生错误分类这种状况的概率，增加聚类的精确度，尽可能多地使各个数据分到正确的簇中。

然后，利用已知的训练集，使用KNN 算法来训练新加入的数据集DS2，再结合使用SC-SNN 算法学习到的特征，建立增量聚类模型，利用当前的增量聚类模型对新数据集进行聚类，得到新数据集的聚类结果，以此构建新的训练集。再使用此训练集训练新加入的数据集DS3，DS3以DS2的方式进行增量学习。以此种方式不断加入新的数据集，直至所有数据集均得到聚类结果。

因为新增数据不仅仅是根据自身的算法得出聚类结果，而是结合在已测试数据集的聚类结果上来预测其聚类的结果，即在根据自身特征进行训练更新的基础上，还会有效地结合学习到的历史数据特征，故对新增数据的分类及预测准确度不断增加。

为了提升谱聚类算法的聚类效果，本文在式（1）的基础上添加了一个平衡项，其中λ称为平衡因子，它的取值往往跟聚类结果密切相关。由此，可以得出该算法的目标函数：

其中，L为Laplacian 矩阵，D称为相似矩阵的度矩阵，y为类标签矩阵。

对于参数λ，应考虑λ=0 的情况。当λ=0 时，即不考虑KNN 算法对聚类精确度的影响，在每一个数据块的聚类过程中，仅依据SC-SNN 算法得出聚类结果。这样得出的聚类效果并不理想。为了提高聚类性能，应将KNN 算法得出的聚类结果考虑在内，即λ≠0的情况，此时平衡项的加入能很好地提高聚类性能。

3.2 算法流程图示及其步骤

根据算法的设计思想，可将ISC-SNN 算法简单概括为图1 所示。

ISC-SNN 算法的具体步骤如下所述：

输入：n个数据点，聚类簇数K，近邻数k，划分子集个数T。

输出：输入数据的簇标记。

步骤1将数据集X分为T个子集，即X={DS1,DS2,…,DST}。

步骤2对初始数据集DS1使用SC-SNN 算法进行聚类，得到聚类结果。

步骤3fori=2,3,…,T

步骤3.1对未进行聚类的其他子数据集DSi调用SC-SNN 算法，得到拉普拉斯矩阵。

步骤3.2参照数据集DSi-1得到的聚类结果，使用KNN方法确定此新增数据集DSi中数据点的类别。

步骤3.3依据式（5）得到此层中的最终指示向量，继而得出聚类结果。

end for

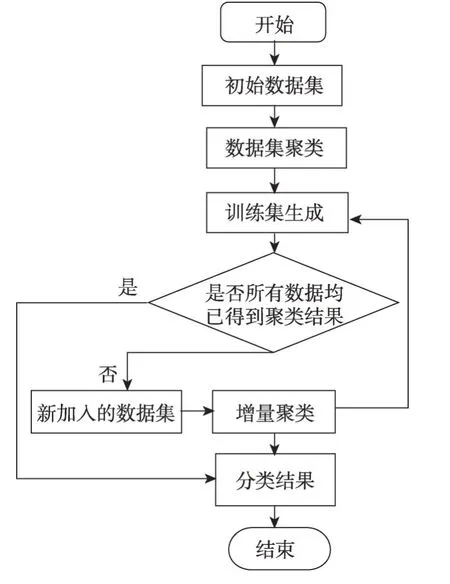
Fig.1 Algorithm process diagram图1 算法流程图示

3.3 算法的时间复杂度

本文中算法的时间复杂度取决于步骤2、步骤3。其中步骤2 的时间复杂度为Ο((n/T)2lbn)。步骤3单次计算的时间复杂度为Ο((n/T)2lbn+(n/T×knum))，其中knum是使用KNN 算法求解数据集类别时所选择的近邻数，而在第3 步的计算次数为T，故这两步的时间复杂度为Ο(n2lbn/T+n×knum)。故可以得知此算法的时间复杂度为Ο((n/T)2lbn+n2lbn/T+n×knum))。可以看出当T值越大时，时间复杂度越低。

4 实验分析

本章将通过人造数据集和真实数据集两种情况对SC-SNN 和ISC-SNN 两种聚类算法进行实验验证。其目的是为了证实ISC-SNN 算法的有效性和优越性。

在本文的实验中，主要使用两个量来评估聚类性能：运行时间以及聚类精度。运行时间为对某一数据集运行一次聚类算法所用时间（在此使用计算机时间）。聚类精度为通过每个数据集的真实簇标记和算法所得簇标记计算出的聚类结果正确率。在使用相同数据集和运行环境的情况下，耗时越少，聚类精度越高则表明算法的性能越好。

SC-SNN 和ISC-SNN 算法中所有的参数都按如下取值：近邻数k，由文献[10]可知，k值的选择对于聚类的精度影响不大，且在大多数情况下，在其值为7 时取得最优值，故本文实验中SC-SNN 和ISC-SNN两种算法的k值均设置为7；KNN 中的K均取7；λ的取值为多次重复实验中，提到的聚类指标的均值达到较好的时候的取值；T为数据集分成的子数据集的个数，需要根据数据量的大小来选取适合的值，其取值情况将在实验结果中给出。

实验环境：Intel Core i3-3240CPU@3.40 GHz，4.00 GB RAM，Windows10，Matlab R2016b 等。

4.1 基于人造数据集的实验

为了方便将聚类结果图形化，给定3 类人造数据集：DS1 是两个圆形的数据集，包含582 个数据点；DS2 是两个半月形的数据集，包含1 200 个数据点；DS3是将两个半月形的数据集DS2扩容为包含30 000个数据点的数据集。由于SC-SNN 算法在数据集容量为30 000 时，算法失效，故仅将其在DS1 和DS2 的数据集下的聚类效果图展示出来。对于DS3，将从中抽取不同容量的子集来运行SC-SNN 和ISC-SNN 两种算法以测试其聚类所需时间和准确度。在实验中，由于聚类的实验结果不稳定，故实验结果均为多次实验后计算的平均值。对于ISC-SNN 中的参数λ分别为2、3；实验结果如图2、图3 所示，不同簇使用不同的颜色来表示。而在表1 中，设置了λ为0 的对比实验，其中在ISC-SNN 的实验结果中，数据的第一行为λ=3 的结果，第二行为λ=0 的结果，在真实数据集中实验结果同样按照此种格式设置。

由上述实验结果可知，当数据量较小时，SCSNN 算法和ISC-SNN 算法都可以得到较好的聚类效果。但当样本容量达到18 000 时，SC-SNN 在运行中发生了内存不足的问题，导致该算法在本文的实验环境中无法顺利运行。而ISC-SNN 算法不仅可以在样本容量不断增大的情况下顺利运行，而且聚类时间明显少于SC-SNN。

4.2 基于真实数据集的实验

真实数据集由于噪声信息的存在，聚类划分的难度要大于人造数据集，对算法性能的验证也更具说服力。在本节，将使用UCI 数据库里的5 个数据集Wifi、Waveform、Musk、MGT、Covertype 来 进 行 实验。数据集的详细信息如表2 所示。

Fig.2 Original graph and experimental graph of DS1图2 DS1 原图及实验图

Fig.3 Original graph and experimental graph of DS2图3 DS2原图及实验图

Table 1 Experimental results of DS3表1 DS3 的实验结果

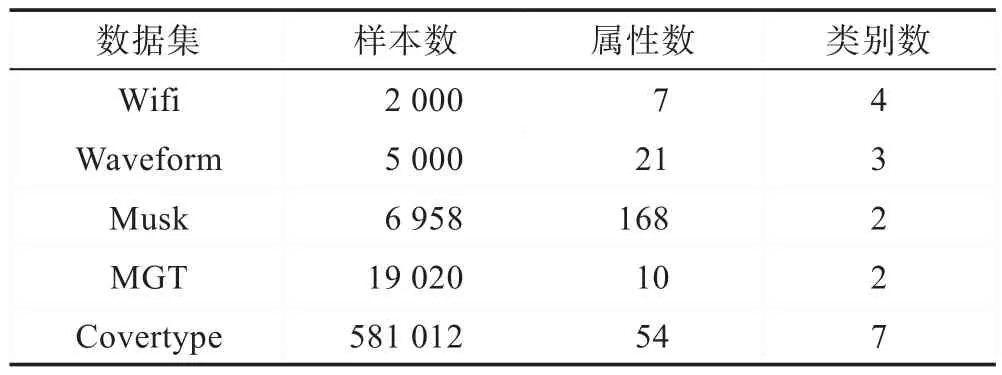
Table 2 Experimental datasets表2 实验数据集

其中，对于3 个数据集Wifi、Waveform、Musk，SC-SNN 算法可以成功执行，故直接对其中的所有样本进行多次重复实验，取其平均值作为实验结果，其中Wifi、Waveform、Musk 中的λ依次设置为3、3、1，并给出与λ=0 的对比。其实验结果如表3 所示，从结果中可以看出，当λ为非零值时，ISC-SNN 相较于SC-SNN 而言，不仅时间缩短了很多，而且聚类精度也明显增加。但当λ为0 时，聚类时间虽然缩短了很多，但聚类精度有可能会下降。由此可知当选取适合的λ时，ISC-SNN 算法在小数据集的聚类问题上可以达到很好的聚类效果。为了进一步验证ISCSNN 的聚类性能的优越性，将使用MGT 和Covertype两个较大一点的数据集，由于样本容量过大，当一次性载入所有样本时会致使SC-SNN 算法失效，故从中分别随机选取若干种不同容量的子集进行测试。关于数据集MGT 和Covertype 中的λ分别设置为2、3，并给出与λ=0 的对比。其实验结果在表4 和表5 中给出。

由上述实验可知，在表4 中，SC-SNN 在样本容量达到18 000 时，计算中发生了内存不足的问题，导致在本文的实验环境中无法顺利运行。由于Covertype的维度比MGT 的维度要高，导致SC-SNN 在样本容量达到15 000 时就发生了内存不足的问题。不难知道，当数据集的维度越来越高时，SC-SNN 算法所能正常执行的容量将会越来越低。而ISC-SNN 算法不仅可以在样本容量不断增大，维度不断升高的情况下顺利运行，在λ为零时，聚类时间虽然有了大幅度减少，但准确度可能会有降低的情况，但在λ为非零值时，聚类时间和准确度都明显优于SC-SNN。此外，从上述实验中能够发现，数据集分成的数据子集越多，精确度越高，聚类所需的时间越短。因此，当样本容量较大时，选择划分的子集数也是很重要的，要想达到快速运行的目的，应该划分较多的子集来进行聚类。

Table 3 Experimental results on dataset Wifi,Waveform,Musk表3 数据集Wifi、Waveform、Musk 的实验结果

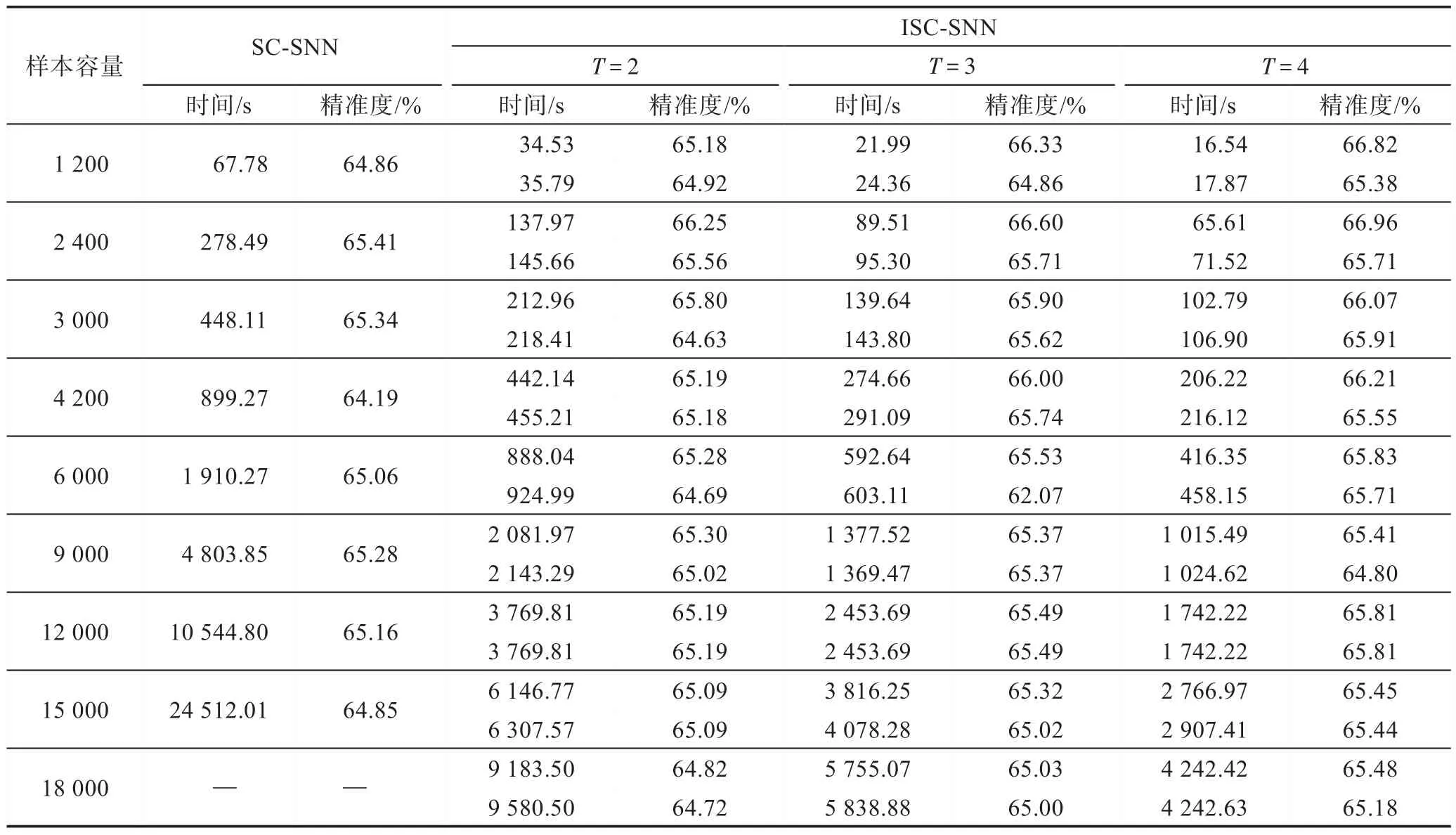
Table 4 Experimental results on dataset MGT表4 数据集MGT 的实验结果

5 结束语

本文提出了一种基于共享近邻紧密度的增量式谱聚类算法。它是在基于共享近邻紧密度的谱聚类算法的基础上，为了能增强精度，减少运行时间并能够适用于大数据的目的上提出的。此算法采用增量式的方法，不仅解决了因内存不足而造成的算法失效问题，而且能在很大程度上提升聚类的性能。尽管此种算法有一定的优点，但仍有许多可改进之处，故在今后的研究中将会对此算法的不足之处进行不断的优化。

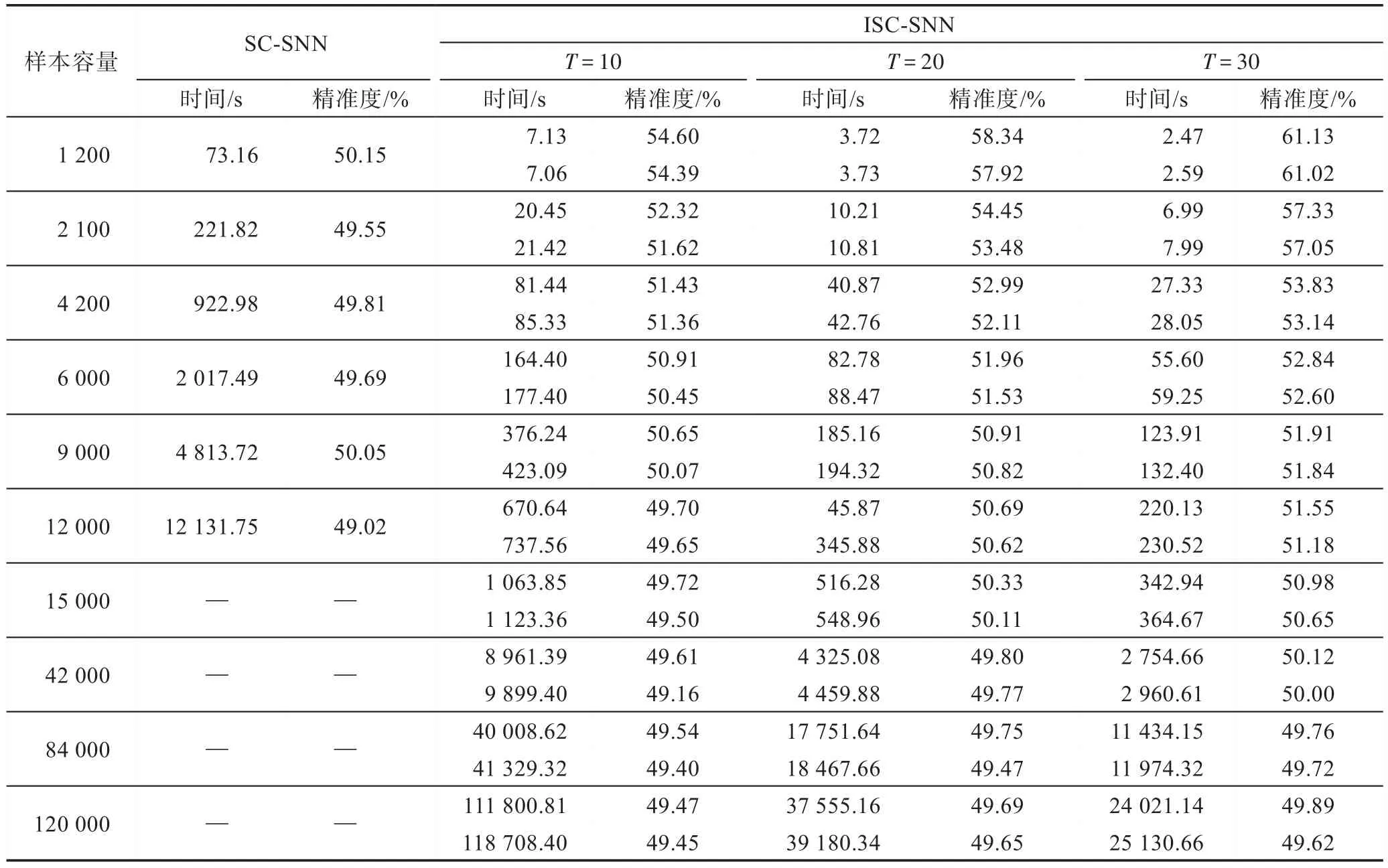
Table 5 Experimental results on dataset Covertype表5 数据集Covertype的实验结果