基于局部均值分解与快速独立成分分析的潜水泵故障诊断

田立勇, 张一辙

(辽宁工程技术大学 机械工程学院, 辽宁 阜新 123000)

1 引 言

潜水泵叶轮瞬时卡挂异物或流道堵塞失衡不畅,都会在短时间内导致潜水泵出现故障,影响工作效率。对潜水泵的振动信号进行快速傅里叶变换,是对潜水泵进行故障分析的有效方法,然而由于潜水泵的工作环境,采集到的故障特征信号容易受到噪声的影响,造成频率混杂现象,传统快速傅里叶变换分析的故障频率往往不明显。

为了提高对潜水泵的故障诊断精度,需要采用合理的方法。目前对于旋转机械等信号处理的方法有很多:付云骁等[1]为提高对滚动轴承故障频率的直观辨识能力,提出了LMD-CM-PCA的方法,为故障诊断的直观辨识提供了支持；马增强等[2]提出的变分模态分解(variational mode decomposition, VMD)与独立成分分析(independent component analysis, ICA)联合降噪的方法,能够清晰准确地提取出故障频率；杜冬梅等[3]针对滚动轴承故障时振动信号的特点,提出局部均值分解(local mean decomposition, LMD)与增强包络谱的方法,能够有效地降低噪声影响；郑慧峰等[4]针对振动信号中的噪声干扰,提出了经验模态分解和奇异值分解的方法,提取出特征信号,实现了损伤诊断和定量评估；付秀伟等[5]针对强噪声下滚动轴承故障特征难以提取的问题,提出了傅里叶分解与奇异值差分谱方法,能够准确地识别出故障特征频率；刘嘉辉等[6]提出了一种同源双通道信噪盲源分离法,该方法能够有效地提取故障特征频率,但具有一定的局限性；张建宇等[7]针对轴承故障的振动特征分离与辨识难度的问题,提出信源估计和频域反卷积的方法,实现了微弱特征识别；孟宗等[8]提出了基于局部均值分解多尺度模糊熵与灰色相似关联度的方法,可以有效的识别滚动轴承的运行状态,实现故障诊断；时培明等[9]针对强噪声下旋转机械的早期故障问题,提出VMD和变尺度多稳随机共振的方法,可以有效提取微弱信号的故障频率；Han T等[10]提出多尺度动态时间规整方法对旋转机械进行故障诊断,并与很多方法进行比较,实验证明该方法的检测准确率较高,能够很好地进行故障分析；汪朝海等[11]基于经验模态分解与主成分分析研究了滚动轴承故障诊断方法。

在对潜水泵进行故障诊断时,特定范围内的频率可以反映出相应的故障。LMD可以将信号分解为一系列的PF分量,通过互相关系数提取出主要的成分,去除部分噪声的干扰。快速独立成分分析(fast independent component analysis, fastICA)可以实现信号的盲源分离,进一步进行降噪处理。2种方法的结合可以增强故障特征频率,解决潜水泵故障早期信号不明显的问题,实现对潜水泵的故障分析与诊断。

2 局部均值分解

局部均值分解本质上是将原始信号分解成一系列的由调频信号和包络信号的乘积表示的乘积函数(product function, PF)分量。这些分量的瞬时频率具有物理意义,包含了原始信号的频率成分[3]。其分解过程如下:

1) 找出原始信号x(t)的每个局部极值点,由式(1)求出相邻2个极值点ni和ni+1的平均值mi,连接所有平均值并通过滑动平均方法得到局部均值函数:

(1)

2) 由式(2)求出包络估计值ai,连接所有包络估计值并通过滑动平均方法得到包络估计函数:

(2)

3) 由式(3)和式(4)得到解调后的s1i(t):

h1i(t)=x(t)-m1i(t)

(3)

(4)

如果a1i(t)=1,即s1i(t)是一个纯调频信号,则进入下一步,否则将s1i(t)作为新的原始信号,重复以上步骤进行迭代,直到满足条件为止,得到最终的s1n(t)。

4) 由式(5)和式(6)得出第一个PF分量:

(5)

PF1(t)=a1(t)s1n(t)

(6)

5) 将PF1(t)从原始信号x(t)中分离出去,得到新的信号μ1(t),将μ1(t)作为新的原始信号重复以上步骤,直到μk(t)为单调函数为止。LMD分解可以将原始信号分解为k个PF分量与一个单调函数μk(t)的和:

(7)

3 快速独立成分分析

基于负熵的快速不动点迭代算法是一种寻找非高斯性最大值的不动点迭代方案。该方法可以将负熵的统计特性和不动点算法的优点结合起来,具有很快的处理速度[12]。基于负熵的梯度算法公式为:

Δw∝γE{zg(wTz)}

(8)

式中:γ=E{(wTz)}-E{G(v)};w为具有单位范数的初始化向量;z为白化后的观测信号;G为任意的非二次函数;g为函数G的导数;v为一个标准化的高斯随机变量。

对负熵梯度算法的公式进行调整,可得出不动点迭代:

(1+a)w=E{zg(wTz)}+aw

(9)

式中a为常数。

由于wTz通常在E{G(wTz)}的极值点处取得近似负熵的极大值,而E{G(wTz)}的极值点可以在式(10)的梯度为零处取得:

F=E{zg(wTz)}+βw=0

(10)

式中β为常数。根据合理的近似可以得出近似的牛顿迭代公式:

w←w-[E{zg(wTz)}+βw][E{g′(wTz)}+β]

(11)

在公式(11)的两边同时乘上β+E{g′(wTz)}进行化简,可以得到FastICA算法中的不动点迭代公式:

w←E{zg(wTz)}-E{g′(wTz)}w

(12)

4 基于LMD与FastICA的故障诊断

基于LMD与FastICA的故障诊断可以按照图1中的几个步骤来完成。1) 用传感器采集对应的振动信号;2) 通过数据采集器的A/D转换模块将模拟信号转换为数字信号;3) 将信号进行LMD,得出一系列的PF分量;4) 计算各PF分量与振动信号的互相关系数;5) 选取互相关系数较大的分量进行重构,并与振动信号组成矩阵;6) 对矩阵进行FastICA处理;7) 将处理后的有效数据进行频谱分析,实现故障分析与诊断。

图1 故障诊断流程图Fig.1 Fault diagnosis flow chart

5 实验分析

在潜水泵正常运行和故障运行时分别测得对应的振动信号,通过对信号进行LMD与FastICA处理验证本方法的正确性。按照图2连接各设备。

图2 潜水泵故障诊断系统图Fig.2 Diving pump fault diagnosis system diagram

实验中的潜水泵采用某制药厂2号线路的潜水泵,其型号为BQW50-20-7-0.75,加速度传感器的型号为澄科CT1005LC。

考虑到潜水泵的结构特点、工作环境以及常见的故障类型,为了有效测得潜水泵工作时的振动信号,将传感器安装在靠近电机轴的外壳上,安装加速度传感器实物图如图3所示。

图3 加速度传感器安装实物图Fig.3 Physical picture of acceleration sensor installation

加速度传感器测得的振动信号经过屏蔽电缆传送到数据采集器中,通过A/D转换模块将模拟信号转化为数字信号,数字采集器通过屏蔽网线与计算机连接,将数字信号传送到计算机中。

本实验中潜水泵的转速为3 000 r/min,工作频率为50 Hz。所以,根据采样定理和以往对监测信号的采集经验[13,14],采样频率为1 000 Hz,采样点数为 1 024 个。采集到的正常信号频域图像如图4所示。

图4 潜水泵正常运行信号频域曲线图Fig.4 Frequency domain curve of submersible pump normal operation signal

图4中48 Hz处为电机频率,图像存在细微的波动,存在噪声影响。为了更有效地模拟出潜水泵运行时的故障,在潜水泵的出水口处添加小木块,制造潜水泵流道堵塞故障。人为制造故障如图5所示。

图5 人为制造故障图Fig.5 Artificial fault map

人为制造故障之后,在故障运行时测得故障信号,经频谱分析后得到的故障运行频谱图如图6所示。

图6 潜水泵故障运行信号频域曲线图Fig.6 Frequency domain curve of submersible pump fault operation signal

根据某制药厂对2号线路潜水泵的长期监测,潜水泵流道堵塞故障会在20～30 Hz之间出现3个明显峰值。潜水泵故障监测图如图7所示。

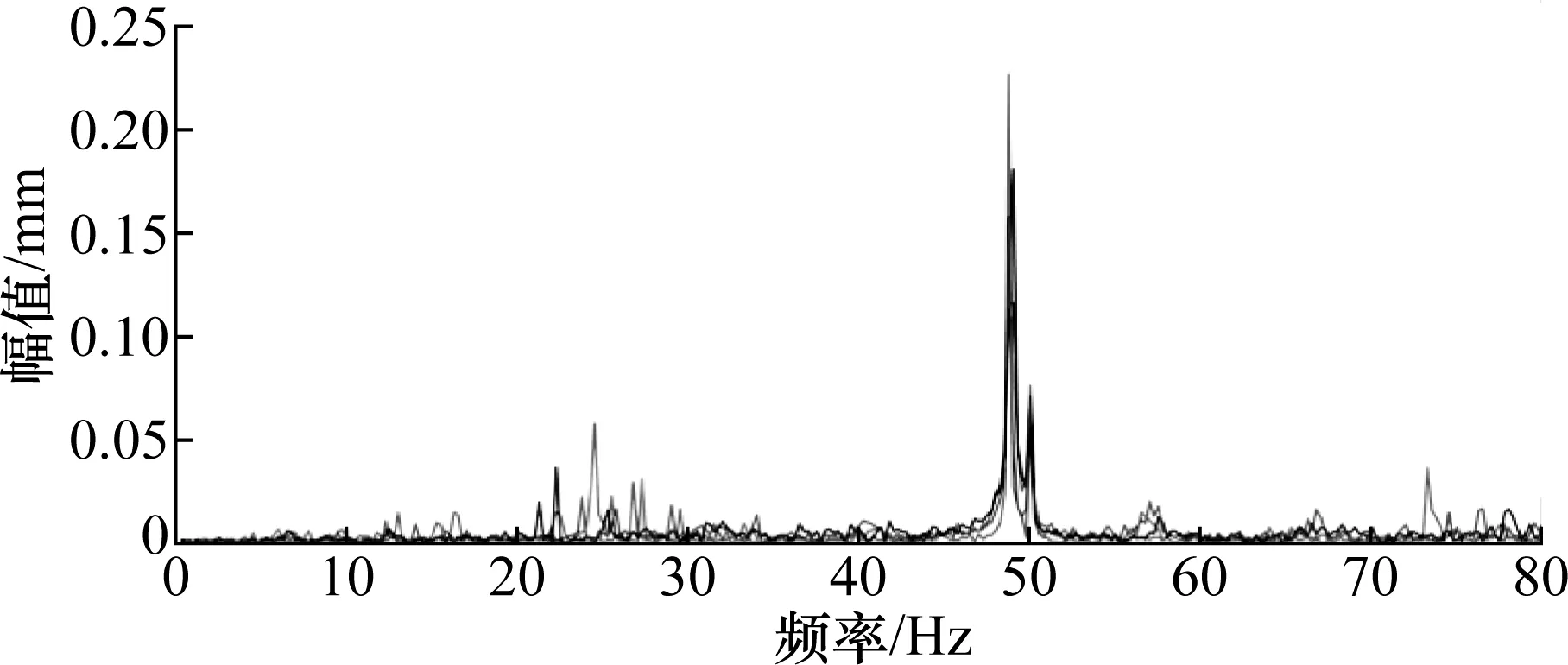
图7 潜水泵故障监测图Fig.7 Submersible pump failure monitoring chart

将正常信号频谱图和故障信号频谱图在低频段50 Hz附近频谱放大,正常信号与故障信号局部频谱图如图8所示。对应尖峰处的频率和幅值如表1所示。

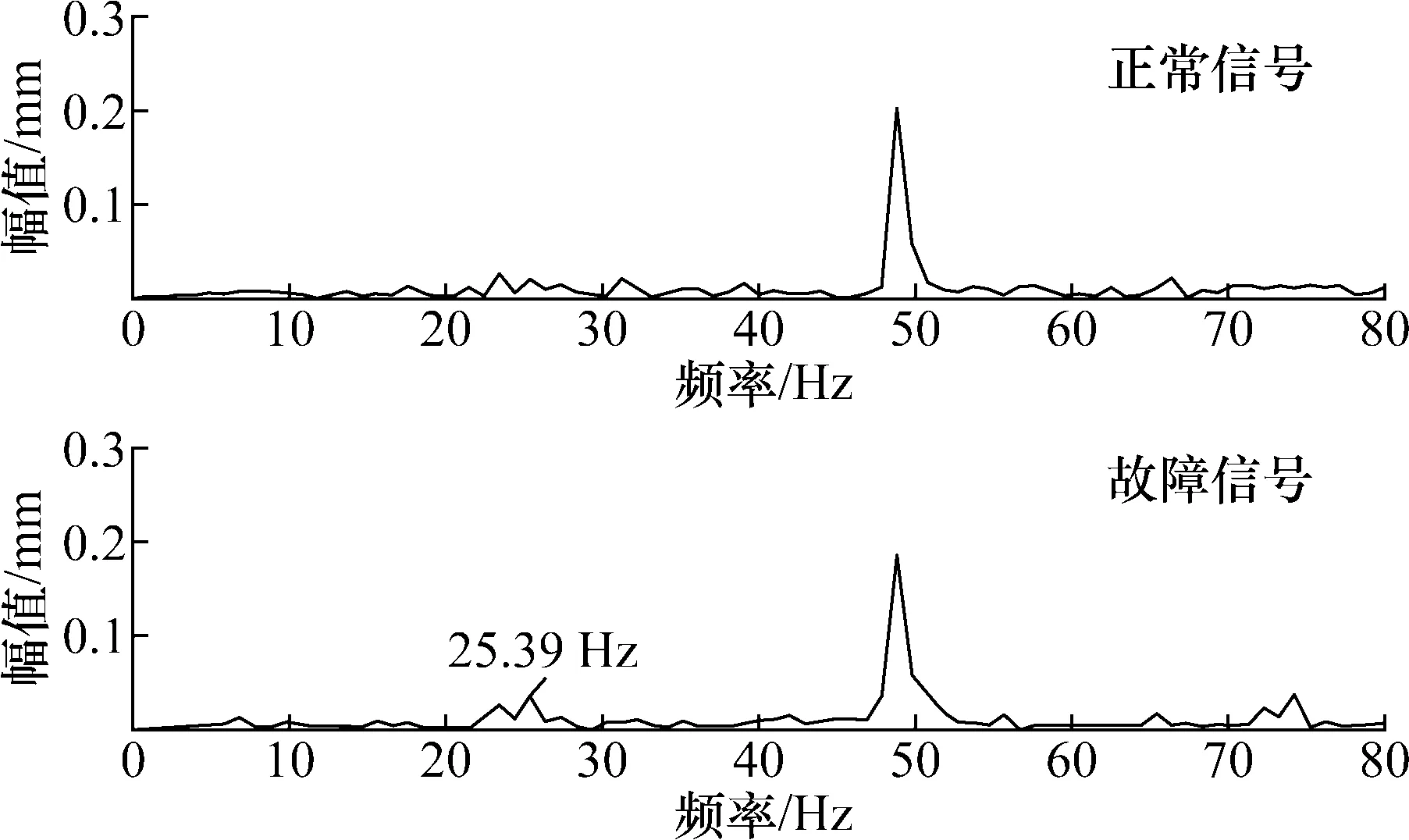
图8 正常信号与故障信号局部频谱图Fig.8 Local spectrum of normal and fault signals

在图8中,正常信号频谱图与故障信号频谱图在 20～30 Hz之间都存在3个尖峰,只是故障信号频谱图在25.39 Hz处尖峰比较明显,而在23.44和27.34 Hz处区分不明显;在表1中,23.44和27.34 Hz处对应幅值比较大,区分不明显,不能准确判断是否出现故障。

表1 未处理的正常信号与故障信号尖峰幅值Tab.1 Peak amplitude of unprocessed normal signal and fault signal

利用LMD与FastICA方法分别对正常信号和故障信号进行处理。先对正常信号与故障信号分别进行LMD,得出一系列的PF分量,正常信号与故障信号的PF分量图如图9、图10所示。

图9 正常信号PF分量图Fig.9 Normal signal PF component diagram

图10 故障信号PF分量图Fig.10 Fault signal PF component diagram

得出分解的PF分量之后,计算各个分量与对应振动信号的互相关系数,根据互相关系数的大小,选取与对应振动信号互相关性较大的分量进行重构。正常信号的互相关系数如表2所示。

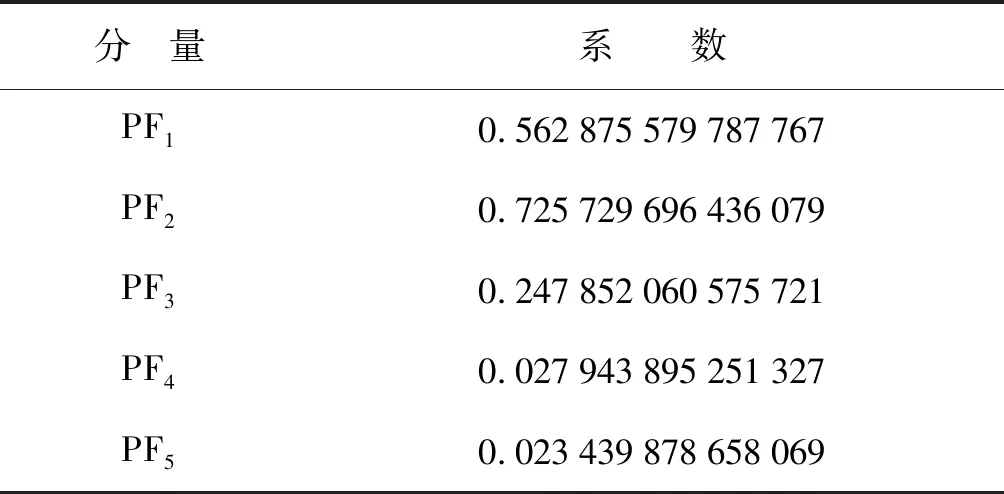
表2 正常信号PF分量的互相关系数Tab.2 Correlation of PF components of normal signals

表2中,PF1～PF3的互相关系数较大,所以对于正常信号,选取PF1～PF3分量重构信号。

故障信号的互相关系数如表3所示。

表3中,PF1～PF3的互相关系数较大,所以对于故障信号,选取PF1～PF3分量重构信号。

将重构后的信号与对应振动信号组成矩阵,对矩阵进行FastICA计算,实现降噪处理。最后对处理后的数据进行频谱分析,得到对应的频谱图。经过本文方法处理后的正常信号与故障信号在50 Hz附近放大的局部频谱图如图11所示。对应尖峰处的频率和幅值如表4所示。信号处理前后幅值比对比图如图12所示。

表3 故障信号PF分量的互相关系数Tab.3 Correlation of PF components of fault signals

图11 LMD与FastICA的正常信号与故障信号局部频谱图Fig.11 Local spectrum of normal and fault signals after LMD and FastICA processing

表4 处理后正常信号与故障信号尖峰幅值
Tab.4 Peak amplitude of normal signal and fault signal after processing

频率/Hz正常信号幅值/mm故障信号幅值/mm幅值比23.440.052710.186350.2828525.390.067650.263720.2565227.340.075940.168430.45087

图12 信号处理前后幅值比对比图Fig.12 Contrast diagram of amplitude ratio before and after signal processing

在图11中,正常信号在20～30 Hz之间无明显尖峰出现,而故障信号在23.44 Hz、25.39 Hz和27.34 Hz处出现明显尖峰;在图12中,处理后的尖峰处幅值比变小,区分明显,由此可以准确判断出故障为流道堵塞故障。

重复上面的步骤对潜水泵塑料块堵塞故障信号进行处理,得出的未处理故障信号频谱图和处理后故障信号频谱图的局部放大图如图13、14所示。

图13 未处理的的塑料块堵塞故障信号频域曲线图Fig.13 Graph of frequency domain of unprocessed plastic block blocking fault signal

图14 本文方法处理后的塑料块堵塞 故障信号频域曲线图Fig.14 The frequency domain curve of the blockage fault signal processed by the method in this paper

塑料块堵塞故障信号未处理和经本文方法处理之后对应尖峰处的频率和幅值如表5和表6所示。

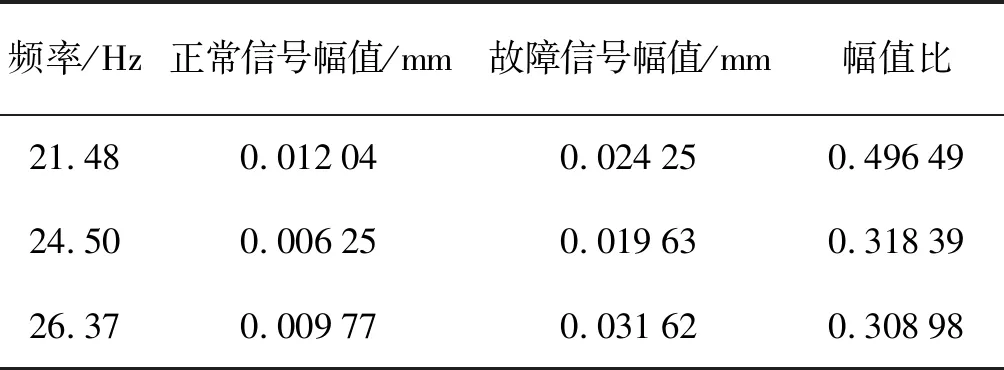
表5 未处理的正常信号与故障信号尖峰幅值Tab.5 Peak amplitude of unprocessed normal signal and fault signal

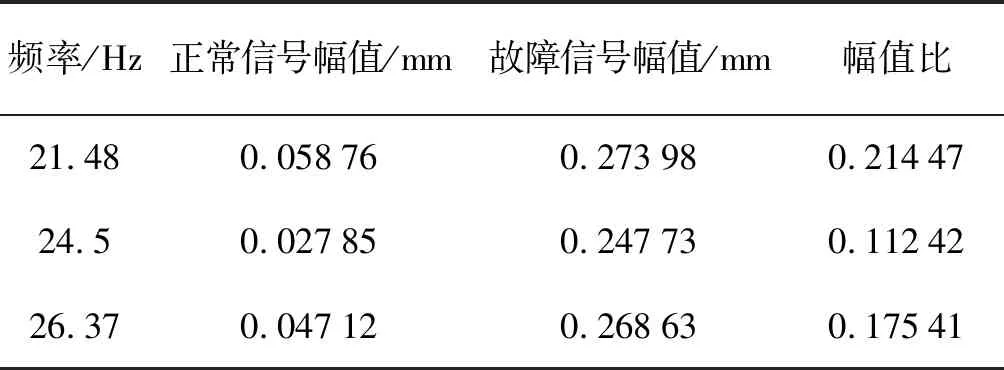
表6 处理后正常信号与故障信号尖峰幅值Tab.6 Peak amplitude of normal signal and fault signal after processing

信号处理前后幅值比对比图如图15所示。

图15 信号处理前后幅值比对比图Fig.15 Contrast diagram of amplitude ratio before and after signal processing

通过信号处理前后图像对比,可以得出本文方法处理后的图像峰值更明显,幅值比较小,能够准确地判断出故障,具有通用性。

6 结 论

本文主要分析了LMD与FastICA方法对于故障诊断的应用,并通过潜水泵的具体实验验证了本方法,得出以下结果。

1)对测得的正常信号与故障信号直接进行频谱分析,并根据潜水泵流道堵塞故障的频率范围进行局部放大对比,正常信号与故障信号在20～30 Hz范围内均有微小尖峰出现,不能准确地判断出故障。

2)经过本文中的方法处理后,对特定范围内的频率进行局部放大对比,正常信号在20～30 Hz之间无明显尖峰,而故障信号在20～30 Hz之间存在3个明显尖峰,可以判断出故障类型为流道堵塞故障。

3)通过对比未处理信号的正常信号与故障信号尖峰处幅值比,以及本文方法处理后的正常信号与故障信号尖峰处幅值比可以得出,经过本文方法处理后的正常信号与故障信号尖峰处幅值比更小,区分更明显。

实验结果表明,LMD与FastICA方法联合可以更加明显地分析故障,提高故障诊断的准确性。