基于四元数最少特征点的相机位姿估计

侯培国， 赵梓建， 宋 涛,2

(1.燕山大学 电气工程学院，河北 秦皇岛 066004； 2.秦皇岛视听机械研究所，河北 秦皇岛 066004)

1 引 言

计算机视觉是利用相机以及计算机来模拟人眼功能，使得计算机智能化，能够从平面图像以及三维立体图像中提取出操作者所需要的有用信息，并进一步做分析处理[1～3]。计算机视觉的应用越来越广泛，而准确的位姿估计在计算机视觉领域中起着十分重要的作用。例如，在计算机视觉的测量中，通过了解相机的位姿变化，可以从一组二维的图像中构建出相应的三维场景模型[4]；在机器人技术中，相机位姿可以用于机器人的导航系统[5]，使得机器人具有“方向感”；除此之外，相机位姿估计在同步定位、自动驾驶汽车以及增强现实等场合中也具有广泛应用[6～8]。

相机位姿估计需要能够在两个或多个图像中检测到图像的特征点并匹配成功，例如图像的边缘、角点等[9]，并且要在空间的一般位置找到至少5个匹配的特征点。当检测并匹配到6个以及更多个特征点进行位姿估计时，位姿估计问题是线性的。而基于5个特征点的相机位姿估计算法(下文简称为5点算法)则必须要解决多项方程组非线性问题[10]。因此，在求解位姿时前一种算法往往比5点算法更快。虽然基于6个或更多个特征点进行相对位姿的估计的执行时间比较短，但是这种算法经常会“失效”，导致算法在许多场景中无法正确求解位姿。例如，利用8点算法进行相机位姿求解时，如果匹配的特征点是共面，或者当相机仅具有旋转动作而平移值为零时，8点算法就不能准确求解。但是5点算法在这样的情况下仍可以很好地求解相对位姿。

许多现有方法使用特征点的坐标来构造基本矩阵，从中可以求解相机的旋转和平移[11，12]。Nister将5点姿态估计问题表述为4个未知变量中的多项式方程组，提出了一种算法，将该系统表示为一个变量的10次多项式，从多项式的根来获得系统的解[13]；Li和Hartley对Nister算法进行了改进，使得改进的算法具有更稳定的数值和更快的执行时间[14]；Kukelova等使用求解多项式特征值的方法进行位姿估计[15]。除此之外，8点算法也是实用的相机运动估计算法之一[16]，算法在基本矩阵中体现的极线约束下，由8个或更多个特征点生成的线性方程组进行位姿估计。

以上方法在进行求解时都是基于基本矩阵来进行位姿估计。但是，当两个相机视图之间的平移值变为零或当匹配的特征点共面时，基于基本矩阵进行位姿估计的方法往往会失去精度[17]。近年来，人们已经提出了独立于平移矩阵来估计相机旋转的新算法,算法不依赖于基本矩阵，从而能避免了相机的旋转和平移纠缠在一起的问题。Kalantari等提出一种独立计算相机旋转和平移的算法[18]，但是该方法效率很低，应用效果不太理想;Kneip等在其基础上提出了一种改进的更有效的算法[19]，但是该算法在相机相对平移较小时很容易受到影响，导致位姿估计的误差较大。

本文提出了一种利用四元数直接估计相机位姿的算法。算法检测相机图像中的特征点，并进行特征点自动匹配，获得特征点的二维坐标。利用四元数表示旋转矩阵R，建立并求解多项式系统。获得四元数的变量值后，进一步求解得到旋转矩阵t和深度信息。对算法在噪声影响下进行测试，并且在多特征点的情况下对算法性能进行了评估，通过与其他常用算法的精度比较显示出文章算法的优越性。最后通过KITTI数据集来测试算法的实际估计精度。

2 相机位姿估计

利用特征点进行位姿估计首先要从相机图像中检测并匹配特征点。如图1所示。相机在不同位置所拍摄的两幅图片，利用计算机在两幅图像中进行特征点的检测和匹配，同时获取特征点的坐标信息。左侧图中检测到的特征点是红色，右侧为绿色。将特征点进行匹配并用黄色线段进行连接，以图像中心为圆心，向右为x轴正方向，向下为y轴正方向，则特征点坐标可知。

图1 特征点匹配图Fig.1 Matched feature points

2.1 多项式方程组的建立

设R∈SO(3)和t∈R3分别表示视图之间相机的相对旋转矩阵和平移矩阵。根据相机在两个视图拍摄的场景图像，可以检测并匹配图像中的特征点，并从图像中提取它们所在图像平面中的坐标。坐标首先以像素为单位获得，然后通过相机校准矩阵将坐标映射到图像平面上的笛卡尔坐标。对于每个匹配的特征点，都遵守刚性运动约束：

uRp+t=vp′

(1)

式中：p，p′∈R3代表两个图像中相匹配的特征点的齐次坐标。标量u和v代表空间中的三维特征点沿着相机坐标系的z轴到原点的距离，称为每个视图处的三维特征点的深度值，如图2所示。点p和p′坐标可以从图像中得到，为已知参数。因此式(1)中需要求解的未知数有u，v，R和t。

图2 不同视角下的特征点Fig.2 Characteristic points from different perspectives

(2)

用四元数的变量表示旋转矩阵，就可以对其直接求解。这里将四元数中的第一个变量定位为非负数，即w≥0，则旋转矩阵和四元数之间存在一对一的对应关系。要进行位姿求解，首先消除未知的参数：u，v和t，并根据四元数的变量导出方程组。通过求解该系统，就可以求解得到旋转矩阵，将所有特征点都代入式(1)可以得到关于平移和深度值的矩阵表达式，对矩阵方程进行求解就可以得到特征点的平移和深度信息。

2.1.1 消除未知参数

对旋转矩阵和平移矩阵求解，首先需要消除方程式中的一些参数。将图像中2个不同的特征点代入式(1)可以得到2个方程式，通过2个方程式相减就可以消除未知参数t。类似的，将3个特征点代入式(1)就可以得到3个方程式，通过公式之间相减就可以消去各个公式中的未知参数t。将图1所示的特征点F1(-0.8，0.3)，F2(1.0，1.4)，F3(2.5，0.9)以及各自相匹配的F′1(-1.3，0.4)，F′2(0.3，1.5)，F′3(1.9，0.8)代入式(1)，可得：

(3)

(4)

(5)

式(3)分别与式(4)和式(5)相减可以得到不含未知数t的方程：

(6)

(7)

将未知数u，v看作未知数，就可以将方程表示为MV=0：

(8)

得到的矩阵M仅由特征点坐标和旋转矩阵R组成，向量V由特征点的深度参数组成。矩阵M的行列式值等于零，对其进行行列式求值，就可以列出关于四元数变量w，x1，x2，x3的4次多项式方程，其系数与特征点坐标有关。多项式方程中不含有未知数u，v，这样就消除了未知的深度参数，如式(9)所示：

(9)

2.1.2 建立方程组

4次多项式方程(9)由35个单项式构成，定义运算：

(10)

则一个拥有c个变量的d次多项式由〈d+c-1，c-1〉个单项式构成。由于任意3个特征点就可以得到一个多项式方程，那么k个特征点可以得到〈k，3〉个方程式。用四元数的变量w，x1，x2，x3分别乘以所得的4次多项式方程，则可以得到更多的多项式方程，如式(11)所示。

(11)

若利用5个特征点来进行相机的位姿估计，则可以确立〈5，3〉=10个4次多项式方程。将四元数变量分别与其相乘，则可以得到40个5次方程式，其单项式的数量为〈4+5-1，3〉=56。

2.2 旋转矩阵的求解

将得到的新方程组用矩阵向量形式表示为：AX=0，其中矩阵A由方程组系数组成，A∈R40×56。矩阵X由所有5次单项式组成，X∈R56。如下所示：

(12)

将向量X分成2个向量：

其中X1∈R35，X2∈R21。X1是包含w的所有单项式的向量，X2则由其余的单项式组成。令A=[A1A2]，其中A1由与X2相关联的A的列组成，A2∈R40×35；并且A2由与X2相关联的A的列构成，A2∈R40×21。则系统AX=0可以等效地写为：

A1X1+A2X2=0

(13)

(14)

将向量X1中的变量w提出，并用V表示，即:

(15)

构造方阵B，B∈R35×35。构造矩阵方程：λV=BV，将问题转化为特征值问题。

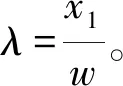
(16)

2.3 平移和深度信息的求解

求得相应的旋转矩阵R后，就可以进一步求解特征点的平移和深度值。所有匹配的特征点都遵守刚性运动约束(1)，则对于k个特征点，将其表达为成矩阵向量形式CY=0：

(17)

式中：I∈R3×3是单位矩阵；k是特征点的数量；矩阵C∈R3k×2k+3，Y∈R2k+3。从式(17)中可以知道矩阵Y在矩阵C的零空间中。通过计算矩阵C的右奇异向量，即CΤC对应的特征向量就可以求解得到Y。向量Y中同时包含了平移信息和深度信息，因此，这些参数可以同时求解得到，并且约束到同一个比例因子。

2.4 算法分析

3 算法性能测试

将算法和几种现有算法进行性能测试。测试利用蒙特卡罗模拟，在相机前方矩形平行六面体内，分别随机生成分布均匀的一般三维点和共面三维点的混合集合。然后通过随机的平移和旋转将相机移动到其他的位置。利用针孔照相机模型，通过将三维空间点投影到图像平面来计算特征点的坐标。文中使用张正友标定法对相机进行标定，并且相机标定所得矩阵为K。每个图像是1 728×668像素。

将文中算法与8点算法、Kukelova算法、Nister算法、Li和Hartley算法以及Stewenius算法[22]进行性能比较。在试验测试中比较各个算法的旋转误差与平移误差来展示比较结果，并将结果绘制成曲线的形式。具体误差计算方法如下：

定义公式：

(18)

式(18)用于描述旋转误差，ρ(q，q*)∈[0，1]。其中q=[wx1x2x3]Τ是测试中用来求解旋转矩阵的四元数值，而q*是真实值。类似地，通过将式中的四元数向量替换为单位范数平移矩阵即可求解得到平移误差。

3.1 抗噪声测试

为评估算法在噪声影响下的性能，实验使用均值为零、标准偏差为0～3个像素的高斯噪声模拟噪声干扰。将其加到所有图像中并设置噪声标准偏差增量值为0.1个象素值，对每个噪声增量值进行100次随机实验。选择最接近真实值的解作为每个算法的估计值。为比较这几种算法在最少特征点时对于噪声的抗干扰能力，实验时为参与比较的算法提供的特征点数目为各个算法求解时所需的最少特征点数量。使用式(18)可得到各算法对应的旋转误差和平移误差，对应的误差曲线如图3所示。

从图3可以看到Nister算法、Li和Hartley算法以及Kukelova算法估计的误差比较接近，因此它们的误差曲线几乎重叠。8点算法展现出了较为良好的平移误差，但是由于其旋转误差太大，图3中只显示了其旋转误差曲线的一部分。Stewenius算法表现出良好的估计精度，在比较中排名第二。本文算法的误差曲线位于所有曲线下方，估计误差要小于其他算法，显示了最佳性能。

图3 抗噪声比较结果Fig.3 Result of anti-noise comparison

3.2 多特征点性能测试

在实际应用中，在两幅图像之间检测和匹配的特征点数量通常大于算法所需的最小数量。因此，在实际应用中，位姿估计算法往往要解决特征点数超过最小值的问题，以减少噪声和错误匹配的影响。实验测试时提供特征点数目为从各自算法所需的最少特征点数到100个特征点来模拟实际中算法匹配到多个特征点的情况，并设置特征点数增量为1。每次增加一个特征点都执行100次比较试验，并且将标准偏差为0.75像素的高斯噪声添加到像素坐标，以模拟图像像素化噪声和特征点检测和匹配中的不准确性。使用式(18)求出对应的旋转误差和平移误差，得到的误差曲线如图4所示。

图4 多特征点性能比较结果Fig.4 Performance comparison results of many feature points

因为Li和Hartley的算法不接受超过5个特征点，因此没有参与比较。如图4所示，在旋转误差曲线图中：当使用特征点数不超过10时，本文算法和Stewenius算法位姿估计精度最好，随着特征点数目增加，8点算法的性能高于Stewenius算法，而本文算法的误差曲线始终位于最下方，具有最好的估计精度；在平移误差曲线图中，当特征点数超过10时，本文算法的估计精度则明显的优于其他参与比较的算法。总体来看，本文算法的旋转和平移估计误差曲线都在其他算法下方，估计精度最高，显示出最佳性能。并且随着匹配到的特征点数量增加，估计结果误差会进一步降低。

3.3 真实数据集测试

为测试算法的实际应用效果，使用来自真实世界数据集的图像测试6种算法，并将估计结果与数据集提供的真实值进行比较。测试采用KITTI数据集[22]。KITTI数据集是最大的计算机视觉算法评测数据集之一，由卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办，包含了城市、乡间、公路等等众多不同的场景下采集的真实图像数据[23]。

使用数据集测试时，在不影响测试结果的前提下，采用抽样原则，对数据集设置增量为5。这样可以缩减测试时间，同时增大视差，更加利于平移信息的估计。所有算法实现都在Matlab中使用C语言进行编程实现，并执行为MEX文件。测试在同一计算机平台上进行。计算机采用Intel(R)Core(TM)i5-8500CPU，主频为3.00 GHz，内存容量为8 GB。结果如表1和表2所示。

表1 平均旋转误差Tab.1 Average rotation error

表2 平均平移误差Tab.2 Average rotation error

为了反映测试结果的统计信息，在表格中列出了平均旋转误差和平均平移误差的四分之一处值，中值以及四分之三处的值，分别用A、B、C表示。同时为了便于比较，表1中的平均旋转误差为放大100倍后的结果。表中数据显示，在参与比较的几种算法中，本文算法的平均旋转误差和平均平移误差均是最小的。与8点算法相比，本文算法的平均旋转中值误差降低了52.9%，平均平移中值误差降低了13.4%。与排名第二的Stewenius算法相比，本文算法的平均旋转中值误差降低了24.5%，平均平移中值误差降低了30.1%。通常来说，使用最少特征点数目大于5的算法往往比5点法算具有更短的执行时间。本文算法执行时间并非最优，但这只是相对而言的。通过真实世界数据集的图像的测试，本文算法完全可以满足应用中的实时性。

4 总 结

文中提出一种基于四元数最少特征点的相机位姿估计算法。对相机图像进行检测并匹配特征点，通过特征点的刚性约束条件建立方程组，从而构建特征值问题来求解相机位姿。算法将特征点平移信息与深度信息约束到同一比例，因此当摄像机视图之间的距离消失时，也可以很好地进行位姿估计。本文算法通过矩阵的伪逆操作来抑制干扰，有效提高位姿估计的精度。利用软件仿真随机生成三维特征点，将本文算法与几种现有的相机位姿估计算法的性能进行了全面比较。在比较中，本文算法的位姿估计精度最优，显著提高了相机旋转与平移估计的精度，并且利用KITTI数据集测试算法的实用性能。将算法估计结果与其所提供的真实值作比较来验证算法精度,从结果可以看出本文算法具有很高的估计精度，能够很好地满足实际应用。