新型旋转角加速度传感器特性标定系统的研究

陆盛康, 冯 浩, 赵 浩

(1.杭州电子科技大学,浙江杭州310018; 2.杭州电子科技大学创新和发展研究院, 浙江杭州310018; 3.嘉兴学院,浙江嘉兴314001)

1 引 言

旋转角加速度能够反映旋转机械系统的运行状态,对于旋转系统运行轴的脉振工况及故障测量、分析及诊断具有重要意义,因此旋转角加速度传感器在机械、交通等领域中具有广泛的应用需求[1]。本课题组前期提出了一种能实时检测旋转轴上旋转加速度的永磁旋转角加速度传感器[2]。但对于旋转加速度传感器的输出特性标定,目前国内机电特性检测机构尚无相应的标准平台,因此影响到该旋转角加速度传感器的推广应用。目前提出的几种标定方法存在着一定的缺陷和局限性,如采用多维线速度合成的方法来标定传感器的方法仅适用于非应变片式角加速度传感器[3～7];另一种多维角加速度传感器的标定是根据质量-转动惯量等效原理,推导等效力计算,从而推导出标定的等效数学模型,但是这种方法局限于传感器静态标定[8];利用重物自由落体的角加速传感器的标定方法理论可行,但是受到标定装置物理结构的限制及阻尼和细绳弹性因素的影响下,精度不能得到很好的保证[9]。本课题组前期提出的一种基于扭摆系统的旋转加速度传感器标定方法与系统[10],虽然该方法与系统对旋转加速度低频特性标定具有一定的精度,但对于旋转角速度传感器中高频特性的标定却无能为力。所以,设计一套适用于旋转角加速度传感器的中高频特性标定的系统是目前迫切需要解决的问题。

本文提出了一种旋转角加速度传感器的标定系统,分析了标定系统振动源产生振动的理论依据,并通过光栅增量式编码器和现场可编程门阵列(field programmable gate array, FPGA)测量系统直接测量出旋转轴上的旋转角加速度[11～13],最后通过峰-峰值对应方式对传感器特性进行标定。该标定系统具有可重复性，振动源的幅值大小可调,保证了传感器的测量范围,具有较好的准确性。

2 永磁旋转角加速度传感器

永磁式旋转角加速度传感器的结构主要包括:内外定子铁芯及由此构成的气隙、杯型转子(介于气隙间)、永磁励磁磁钢、输出绕组等,其结构简图如图1所示。

图1 永磁旋转角加速度传感器原理图Fig.1 Permanent magnet rotation angle and speed sensor schematic

该传感器的工作原理是:杯型转子与传感器转轴同轴相连,传感器转轴与被测转轴同轴相连,内部永磁磁钢产生恒定的磁通Φ1;当旋转系统以恒定的速度n运行时,旋转的杯型转以恒定的转速n切割永磁磁通Φ1,产生恒定的感应电动势e′和电流i′,从而产生磁通为Φ2的恒定磁场;由于磁通Φ2是恒定的,虽然磁通Φ2与输出绕组相铰链,但是由于磁通Φ2恒定,所以输出的绕组中并没有感应电动势产生,e0=0。

当旋转系统中存在旋转角加速时,转子的导条转速n存在变化的转速分量Δn,即存在机械角加速度的变化分量ΔΩ,此时,转子绕组切割恒定的磁场Φ1,产生的感应电动势也会产生相应的变化分量Δe′,由于变化的感应电动势Δe′产生变化的电流分量Δi′,变化的电流分量产生变化的磁场分量ΔΦ2,而变化的磁场分量ΔΦ2与输出绕组相铰链,所以,此时输出绕组的感应电动势e0≠0,并且输出绕组的感应电动势与被测旋转机械系统中的角加速度成正比:

(1)

3 标定平台设计及振动源理论分析

3.1 标定方法与系统

对于旋转角加速度传感器的标定,主要通过传感器与标准脉振源同轴连接,通过对传动轴上的旋转角加速度的高精度测量,将传感器输出电压与实际轴旋转角加速度的比较,从而实现对传感器的标定。

从电力拖动系统的扭转振动的产生原理入手,可以得到旋转系统运行时的转矩平衡方程:

(2)

由于旋转角加速度传感器转子的阻尼力矩很小,而且对于某一点工作点的特性标定时传感器是一个恒速度恒转矩的负载,所以传感器接收到的旋转振动特性就由标定系统的振动源信号特性所决定。因此在设计标定系统的过程中,振动源的选定尤为重要。

系统选定单相异步电动机纯单相运行作为旋转角加速度的振动源,并通过调频调压电源对其进行供电,调节振动源振动波的频率和幅值,考虑到当采用脉冲宽度调制(pulse width modulation,PWM)的变频调速调压电源对纯单相异步电动机进行供电驱动时,由于电源本身存在高次谐波电压分量,会造成纯单相异步电动机输出转矩中产生附加的高次谐波脉动转矩分量,对传感器的特性高精度标定产生不利,因此采用变频电源驱动三相异步电动机,由三相异步电动机驱动交流发电机,再由自耦调压变压器进行调压构成调频调压电源,驱动纯单相异步电动机。

在此基础上,要对异步电动机输出轴上的实际旋转角加速度进行测量,为此,构建基于FPGA的光电编码器旋转角加速度测量分析系统,采用高精度光栅编码器测旋转角加速度的方法测量旋转轴上的不同频率不同幅值条件下实际旋转角加速度变化情况;同时,测量对应频率、幅值条件下永磁旋转加速度传感器的实际输出电压波形;通过对不同频率不同幅值条件下旋转轴实际旋转角加速度与永磁旋转加速度传感器输出电压峰-峰值进行对比分析,从而实现了对永磁旋转角加速度传感器的标定。图2是标定系统的结构框图。

图2 标定系统结构框图Fig.2 Calibration system block diagram

3.2 电机纯单相运行时转矩特性分析

纯单相异步电动机模型如图3所示,该模型是指单相异步电动机仅在主绕组m的通电情况下运行分析,纯单相设电机纯单相运行时的电源电压为:

U=Vmsinωit

(3)

式中:ωi为电源角频率;Vm为电源电压幅值。

则定子绕组中产生的电流为:

(4)

式中:φm为定子绕组的输入电压与输入电流的相位差;Zm为主绕组的输入阻抗。

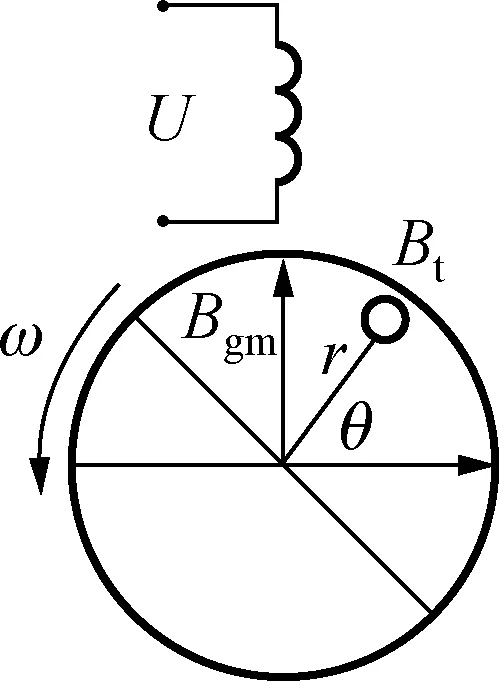
图3 纯单相异步电动机模型Fig.3 Pure single-phase asynchronous motor model

定子电流产生的气隙磁密为:

Bgm=Bmlsin(ωit-φml)

(5)

式中:Bm1为主绕组电流产生的磁感应强度幅值;φm1为等效的直轴绕组电压与其电流的相位差。

设电动机气隙均匀,转子半径为r,有效长度为l,假设该转子上一根导体以角速度ω逆时针旋转,时刻t时该导体的位置为θ=θ0+ωt,(θ0为导体位置的初始角度)则作用在该导体上的气隙磁密为:

Bt=Bgmsinθ

=Bm1sin(ωit-φm1)sin(θ0+ωt)

=Bmfcos ((ωi-ω)t-φm1-θ0)-

Bmbcos ((ωi-ω)t-φm1+θ0)

(6)

式中:Bmf为气隙磁场磁密的正序分量,Bmb为气隙磁场磁密负序分量。

此时转子导体感应电动势为E=Blv,转子导体电流i=E/Z,因此,此时转子导体电流:

(7)

转子电流与气隙磁场相互作用产生转矩,设转子的总导体数为Nr,则转子所产生的转矩为:

=T(Bmf1,Imf1)+T(Bmb1,Imf1)+

T(Bmb1,Imf1)+T(Bmf1,Imb1)

(8)

式中:Bmf1为正序旋转磁场;Bmb1为逆序旋转磁场;Imf1为正序转子电流;Imb1为逆序转子电流。

对式(8)进行展开可以得到:

(9)

式中:φmb10为主绕组输入电压逆序分量与励磁电流间相位差;φmf10为主绕组输入电压正序分量与励磁电流间相位差;φf1为一根转子导体正序分量阻抗角;φb1为一根转子导体逆序分量阻抗角。

由式(9)可以得出:正序旋转磁场与正序转子电流之间相互作用,产生正序转动力矩;逆序旋转磁场与逆序转子电流之间相互作用,产生逆序转动力矩;正序旋转磁场与逆序转子电流之间相互作用,逆序旋转磁场与正序转子电流之间相互作用,产生二倍频率的脉动转矩。具体如表1所示。

表1 纯单相运行转矩特性Tab.1 Pure single-phase running torque characteristics

脉动转矩的幅值与正逆序旋转磁场磁密及正逆序转子电流的大小有关,随着电动机外加电源的电压改变,电动机轴上产生的脉动转矩也会发生变化,图4是实验样机在50 Hz不同电源电压有效值激励下电动机输出脉动转矩峰值的变化曲线。

图4 振动源脉动转矩峰值变化曲线Fig.4 Vibration source ripple torque peak curve

因此,纯单相异步电动机可以作为标定系统的脉动转矩源。

4 光栅旋转角加速度测量系统

4.1 光栅测量旋转角加速度原理

(10)

第i个方波脉冲的时间宽度ti的测量通过高频脉冲插值计数实现,其原理如图5所示。根据连续的各个光栅格的旋转角加速度量就可绘制旋转角加速度曲线。

图5 高频插值计数原理Fig.5 High frequency interpolation counting principle

4.2 FPGA高频脉冲测量系统

为了通过增量式光栅编码器实现对旋转角加速度量的测量,构建了如图6所示的基于FPGA的数据测量系统。

如图6所示,对于来自光栅的一串方波脉冲通过二分频电路实现第i个光栅格对应时间宽对应于方波脉冲的高电平或低电平;并通过FPGA内部的PLL锁相环,将测量系统晶振的50 MHz频率倍频至200 MHz,作为光栅格计时的高频插值计数脉冲,为了连续读取各个光栅格所对应的高频脉冲计数信号,这里采用计数器1和计数器2两个32位计数器交替工作,采用FPGA设计中常用的乒乓操作和流水线设计思想,计数器1对方波脉冲的高电平进行计数,计数器2对方波脉冲的低电平进行计数;然后将计数器1和计数器2的值交替送入异步FIFO中进行缓存,设置异步FIFO目的是为了保证传输数据的准确性和传输速率匹配;由于FIFO中是32位数据,而串口发送一次只能发送8位数据,因此设置数据选择模块对数据进行选择,使每一次传输8位数据,自高而低进行传输;最后是串口发送模块,将采集到的数据发送给上位机,进行数据处理与分析。

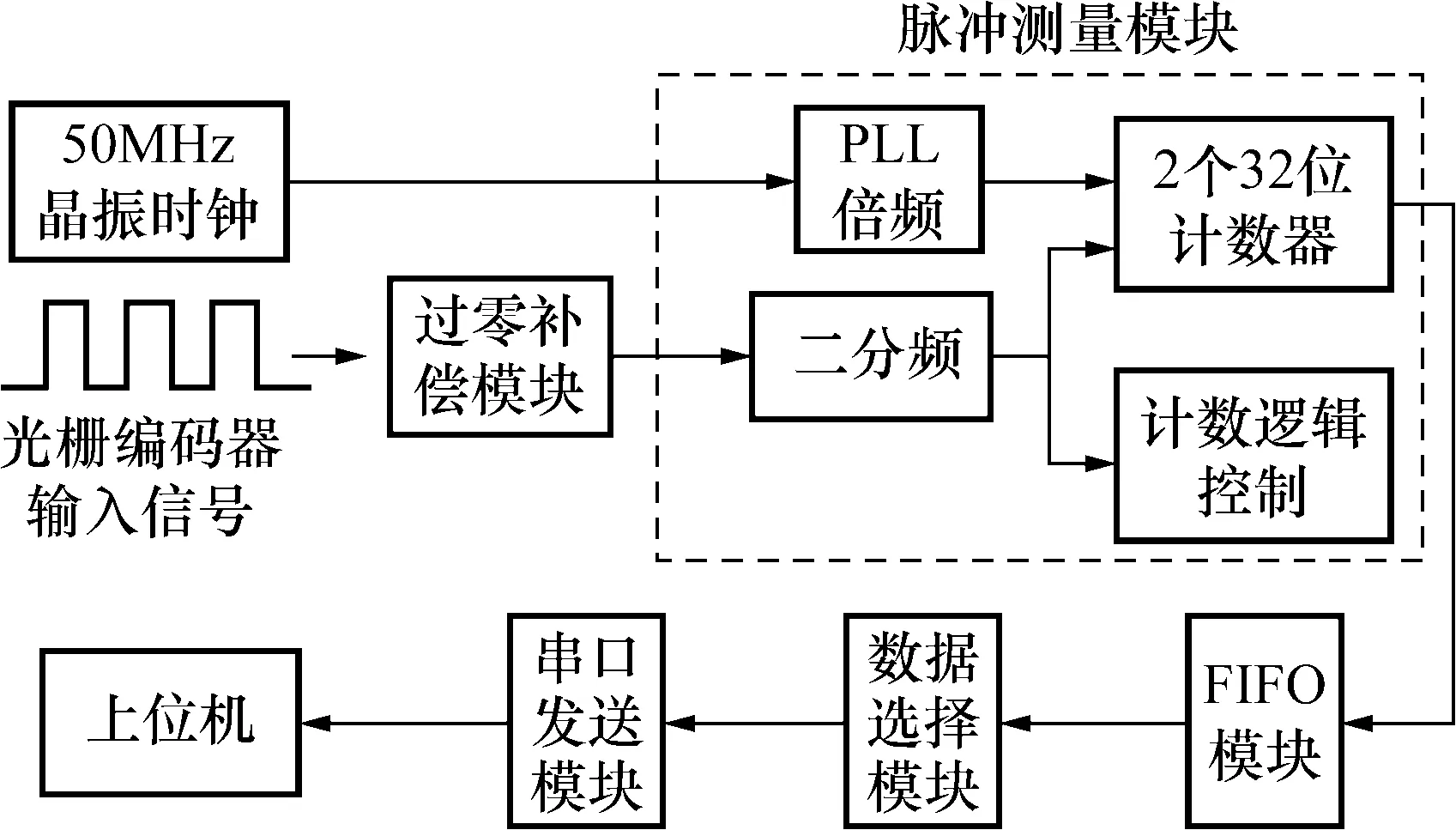
图6 基于FPGA的旋转角加速度测量系统框图Fig.6 FPGA-based rotating angular acceleration measurement system block diagram

5 传感器特性标定与实验结果

对于图2的系统框图,构建了如图7所示的实验平台,为了减小工作平台对实验结果的影响:1) 关键实验置于磁悬浮的支撑平台上,将单相异步电动、轴套式永磁旋转(角)加速度传感器以及增量旋转编码器K10042同轴相连;2) 由变频电源、电动机、交流发电机、调压器所构成的调频调压电源对单相异步电动机进行供电。

图7 旋转角加速度整定平台Fig.7 Rotational angular acceleration setting platform

运行时,先通过起动绕组对单相异步电动机进行起动运行,然后切除起动绕组电动机进入纯电动运行状态,最后通过调频调压以电动机输出不同振动特性的脉动转矩,使永磁旋转加速度传感器及光栅编码器接收到旋转轴不同的旋转角加速度特性。

5.1 旋转角加速度传感器输出及分析

图8是永磁旋转角加速度传感器在电机运行电压220 V时的输出电压波形,可以看出传感器具有较高的信噪比。

图8 传感器输出波形图Fig.8 Sensor output waveform

图9是其输出电压波形频谱图,并且通过旋转角加速度曲线的频谱分析结果可以验证纯单相异步电动机具有二倍基波频率的振动特性。图10是去除高低频谐波后振动基波的输出电压波形图。

图9 传感器输出波形频谱分析Fig.9 Sensor output waveform spectrum analysis

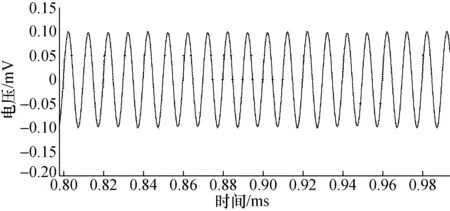
图10 传感器输电压基波波形图Fig.10 Sensor transmission voltage fundamental waveform diagram

5.2 光栅角加速度测量系统输出及分析

图11是根据光栅角加速测量系统记录数据,通过分析计算获取的电机运行于220 V时轴上旋转角速度及旋转角加速度变化波形,很明显可以看到:旋转角速度过零时旋转角加速度变化最大,角加速度的曲线相位超前旋转角速度曲线90°,并且对旋转角加速度曲线进行频谱分析进一步验证了理论分析二倍基波频率的振动。

图11 角速度-角加速度波形图Fig.11 Angular velocity-angular acceleration waveform

光栅-旋转角加速度频谱分析结果如图12所示。图13是去除高低频谐波后振动基波的光栅-旋转角加速度波形图。

图12 光栅-旋转角加速度频谱分析Fig.12 Grating-rotation angular acceleration spectrum analysis

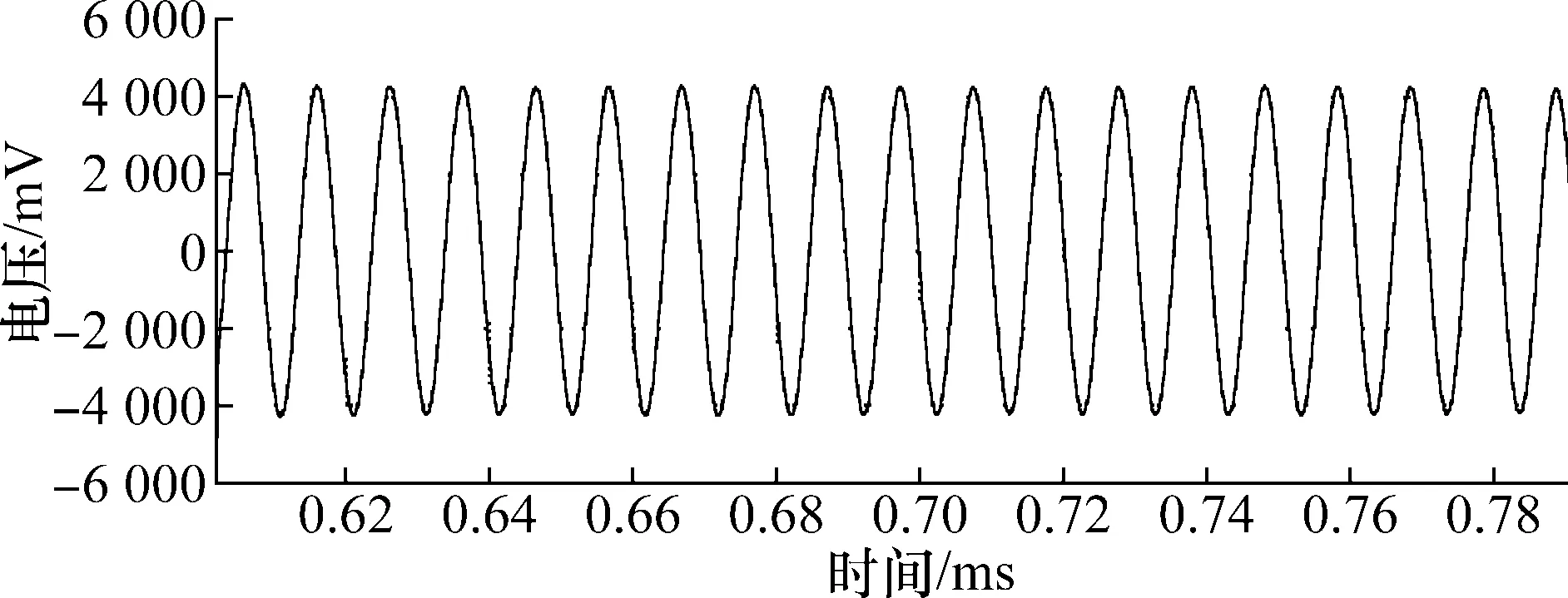
图13 光栅-旋转角加速度基波波形图Fig.13 Grating-rotation angular acceleration fundamental waveform diagram

5.3 标定结果与数据分析

传感器的输出电压和光栅旋转角加速测量系统测量计算获取的旋转角加速度波形数据就可以对传感器的特性进行标定。为了便于分析比较,采用峰-峰值对应的方法进行标定,即将旋转角加速度峰值-传感器的输出电压峰值一一对应。

由于光栅旋转角加速度测量系统测量的角加速度曲线及传感器的输出电压波形都包含一些高频的噪声信号,所以需要对高频噪声信号进行滤波处理,并通过脉动波形的基波幅值进行对应比较,为了进一步探讨其它工作点的特性,用同样的方法在120～220 V之间对传感器进行11次测量,其结果如表2所示。传感器输出电压与旋转角加速度标定特性曲线如图14所示。

表2 120～220 V标定量测量结果Tab.2120～220 V standard quantitative measurement results

图14 传感器-角加速度标定曲线Fig.14 Sensor-angular acceleration calibration curve

6 结 论

本文主要针对永磁旋转角加速度传感器的标定问题开展研究工作,主要研究内容如下:

1) 设计提出了一个永磁旋转角加速度传感器标定平台;

2) 研究建立纯单相异步电动机旋转振动转矩的数学模型,提出并搭建了一个可重复的、幅值可调的、频率可调的旋转角加速度量的振动源;

3) 设计开发了基于光栅编码器-FPGA的旋转角加速度测量系统,对永磁旋转角加速度传感器输出特性进行了标定,标定结果的线性误差为1.81%。

本标定平台对于其他类型的旋转角加速度传感器也可以进行重复性标定实验,具有一定的工程应用价值。