不同传热方式下温度传感器动态特性研究

贾 超， 蔡 杰， 熊朝晖

(中国工程物理研究院计量测试中心，四川绵阳621900)

1 引 言

温度传感器作为动态温度测量的主要测量手段，其动态特性是影响动态温度测量准确性的重要参数[1，2]。为了确定动态特性参数，国内外学者进行了大量研究，形成了投掷法(油浴法、水浴法)[3～5]、激波管法、电加热法[6]、热风洞法[7，8]和脉冲激光法[9～11]等动态测试方法，但至今仍未形成统一的动态特性参数标定方案。究其原因主要是在实际测量过程中，动态温度场环境较复杂，各种传热过程同时发生，实验室条件下测量的动态特性参数与实际值差别较大，无法完全满足实际需求[12]。因此，研究不同传热方式下温度传感器的动态特性对于温度传感器在动态温度测量领域的研究和应用具有一定的参考价值。

传感器的动态响应特性是指温度传感器的温度与被测介质温度增量之间的关系，其特征参数主要有热响应时间和时间常数。热响应时间是影响测试结果的重要因素，而时间常数是反映其动态响应性能最重要的指标[13]。

本文以工业热电偶为研究对象，通过时间常数理论推导，分析时间常数的主要影响因素；根据时间常数推导结果研究不同传热方式与动态特性之间的关系，并通过理论推导结合实验验证的方式分析了不同传热方式下温度传感器的动态响应特性，实验结果验证了理论推导的正确性。

2 时间常数

假设将体积V、密度ρ、比热容c、表面积S的热电偶放置于温度为Te的恒定温场中，动态平衡时热电偶的能量方程可表示为：

qh=qc

(1)

式中：qh为对流传热量；qc为热电偶热结点储热量。

经过时间t后，热电偶指示温度为T，那么：

qh=Sh(Te-T)

(2)

(3)

式中：h为热电偶与温场介质之间的表面传热系数。

将式(2)、式(3)代入式(1)式得：

(4)

在初始条件t=0，T=T0时，对式(4)积分简化可得：

(5)

(6)

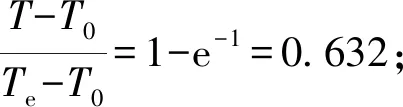
图1 热电偶阶跃响应曲线上的时间常数Fig.1 Time constant on the thermocouple step response curve

从表达式可以看出，时间常数是一个多影响量参数，除了传感器自身特性(材料、结构)的影响外[14]，传感器与温场介质之间的表面传热系数为主要影响量，即传热方式。

3 不同传热方式下的动态特性分析

为了得到正确的时间常数值，分析不同传热方式下热电偶的动态响应成为关键。目前热电偶时间常数的测试方法主要有热风洞法、水浴法、油浴法和脉冲激光法等，按传热方式可分为对流传热和辐射传热[15]。

3.1 对流传热方式下的动态特性分析

当采用热风洞法、水(油)浴法作为阶跃温度激励方法时，忽略自身热传导，热电偶与外界的主要传热方式为对流传热。无论对流传热过程的具体特性如何，其能量平衡方程可用牛顿冷却公式表示：

(7)

式中：h1表示热电偶与硅油之间的表面传热系数。

3.2 辐射传热方式下的动态特性分析

当激励方式为脉冲激光时，激光主要以辐射传热作用在热电偶表面，但随着温度的升高，热电偶会以对流传热的方式与周围空气发生热交换。根据能量守恒关系，热电偶的能量平衡方程可表示为：

Q-(QF+QD)=qc

(8)

式中：Q表示热电偶吸收激光能量；QF表示热电偶受激光照射的净辐射换热量；QD表示热电偶与周围环境的换热量。

根据斯特藩-玻尔兹曼定律可得：

(9)

式中：α为热电偶吸收率；ε为热电偶表面发射率；σ为斯特藩-玻尔兹曼常数；G表示辐照功率；E表示发射功率。

对热电偶而言，若忽略自身热传导，在瞬态条件下其能量平衡方程可表示为：

(10)

式中：αI为热电偶对激光的吸收系数；I为激光的功率密度；h2为热电偶与空气之间的表面传热系数。

式(10)是一个非线性、一阶、非齐次常微分方程，无法积分得到严格解，但利用数值积分方法或有限差分方法可以得到该微分方程解。

4 实验系统与实验数据

4.1 实验系统

为了获取对流传热和辐射传热方式下热电偶的动态响应，分别建立了基于恒温油槽和脉冲激光器的时间常数测试系统，其系统装置如图2所示。

图2 时间常数测试系统Fig.2 Time constant test system

热电偶动态响应测试系统激励源分别选用湖州晶觅试验设备有限公司HTS-300A型号恒温油槽和北京镭志威光电技术公司研制的连续激光器，数据采集装置为Agilent DSO8104A型数字示波器，采集速率为4 GSa/s。实验过程中，将示波器设置为滚动采集模式。采用投掷法将热电偶测量端突然置于激励温场中，确保热电偶输入为温度阶跃信号，同时示波器采集得到热电偶电势输出值与响应时间曲线。

4.2 实验数据

本文选用重庆川仪一厂WRNK型热电偶为实验对象，其有关参数为热结点直径D=2 mm，导热系数λ=20 W/(m·K)，比热容c=400 J/(kg·K)，密度ρ=8 500 kg/m3。

在对流传热方式下，采用恒温槽作为温度激励源，介质为有机硅油，其传热系数h=1 100 W/(m2·K)，根据集总热容应用条件[16]，热电偶毕渥数Bi=hLc/λ=0.03<0.1(Lc称为定性长度，其值近似等于D/3)，采用集总热容法是极好的近似，因此在对流传热方式下研究热电偶动态特性时可忽略其自身热传导带来的影响。设定恒温油槽温度100 ℃，温度波动度小于0.02 ℃/10 min，在稳定环境温度下，将热电偶突然置于恒温槽中，产生一个80 ℃的温度阶跃信号，示波器采集热电偶动态响应曲线如图3所示。

图3 阶跃温度80 ℃时热电偶输出响应曲线Fig.3 Thermocouple output response curve at step temperature 80 ℃

由对流传热方式下热电偶能量平衡方程可知，80 ℃油浴阶跃输入信号下热电偶的时间常数理论值为1.0 s。由图3可知，相同条件下热电偶达到动态平衡时的时间为6.2 s左右，由时间常数的定义可得时间常数实际测量值为1.2 s，与理论值基本一致。

在辐射传热方式下，热电偶与周围空气发生热交换，其传热系数为h=20 W/(m2·K)，同理可得毕渥数Bi=hLc/λ=2×10-3<0.1，因此可忽略自身热传导。该方法采用连续激光器作为激励源，输出波长为1 064 nm，输出功率0～5 W可调，出光孔光斑<5 mm，输出功率稳定性小于1%。常温下，设置激光器输出功率5 W，并聚焦至热电偶热结点上。数字示波器采集到的动态响应曲线如图4所示。由图4可以看出，达到动态平衡时热电偶热电势变化值为11.78 mV，根据K型热电偶电势值-温度换算公式可得阶跃温度为290 ℃。

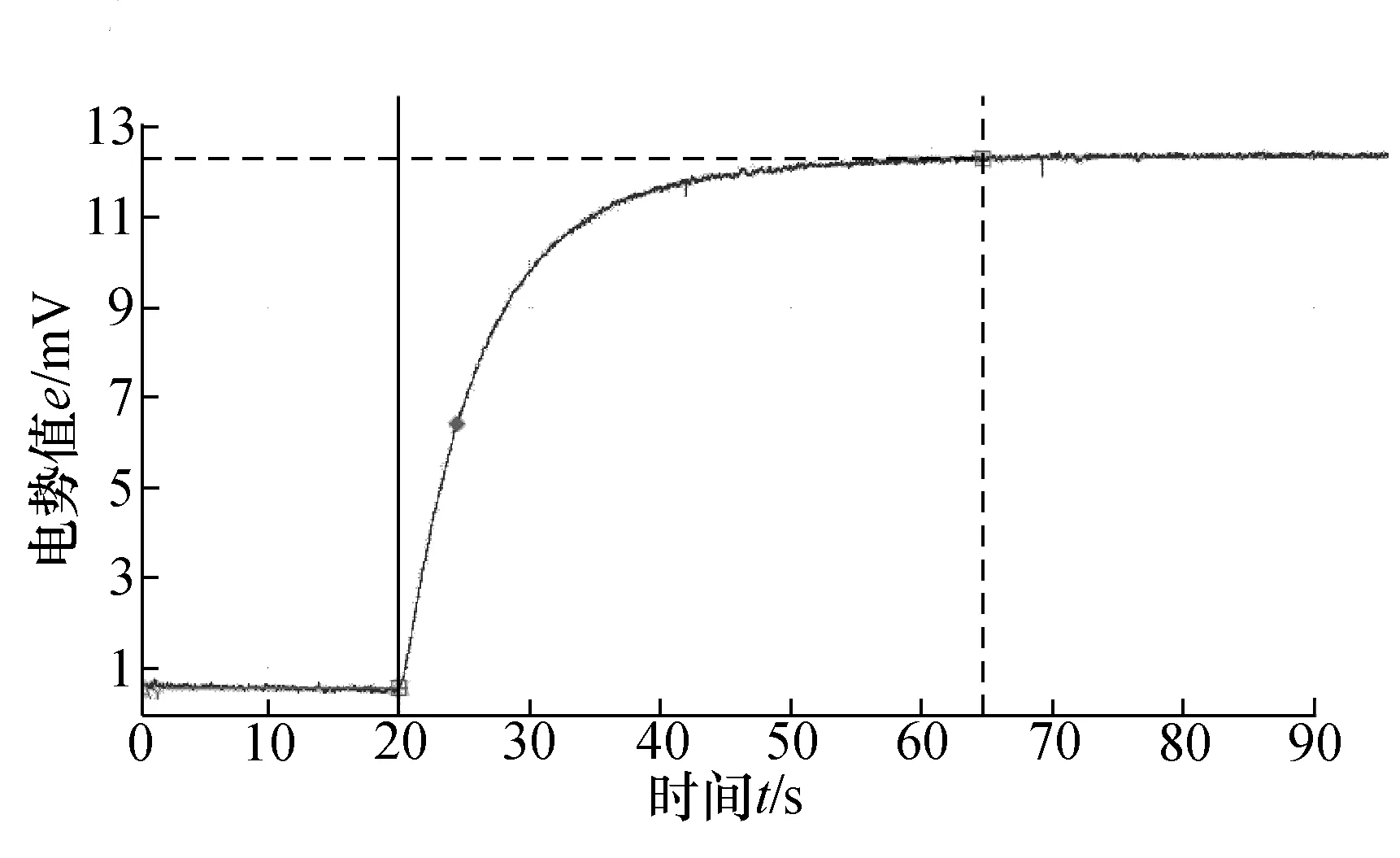
图4 激光输出功率5 W时热电偶输出响应曲线Fig.4 Thermocouple output response curve with laser output power of 5 W

根据式(10)，采用数值积分方法，可得在辐射传热方式下热电偶的理论时间常数为4.3 s；根据时间常数定义，从图4可以看出达到温度阶跃量的63.2%时实际测量时间常数为6.2 s。

5 结 论

针对不同传热方式下温度传感器的动态响应问题，本文以K型工业热电偶为研究对象，从时间常数的定义出发，分析其影响因素除了传感器本身外，与温场介质间的传热系数为主要影响量；然后通过理论推导对流传热和辐射传热方式下热电偶的能量平衡方程，分析其动态特性，并开展了两种传热方式下的时间常数测试实验，从实验结果可以看出，在对流传热方式下，热电偶时间常数理论值与实际值基本一致；但在辐射传热方式下，热电偶对激光能量的吸收情况决定了时间常数测试值的大小，影响因素较多，导致时间理论值与实验值存在较大偏差。因此在研究温度传感器动态特性时，要充分考虑传热方式的不同对测量结果带来的影响，根据实际环境条件确定传热过程，以确保测量结果的准确性与可靠性。