基于现场试验的高铁路基智能压实过程中振动波垂向传播机制

蔡德钩，叶阳升，闫宏业，魏少伟，尧俊凯

（1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081；2.中国铁道科学研究院集团有限公司,北京 100081）

路基结构作为铁路基础设施重要的组成部分,路基线路长度占铁路总里程的比例超过30%。随着我国高速铁路的迅速发展,对路基结构的稳定性和坚固性要求不断提高,迫切需要在路基填筑过程中对其压实质量进行严格的控制。近年来,在“智能京张”、“智能京雄”等高铁线路的建设过程中,高铁路基压实技术也从传统的质量控制发展至智能压实控制,并在京雄高铁的固安段、郑徐高铁的周口段等工点先后开展了大量工程化工作。

目前,国内外学者在路基填料和智能压实方面进行了大量研究［1-5］,提出的压实控制指标主要有压实计指标［6］和动力学指标［7］2 类。压实计法主要是对振动轮竖向加速度进行傅里叶变换,通过判别振动轮垂向加速度响应的频谱特征评定被压填料的压实质量［8］。然而,振动信号是一个复杂的非平稳信号,振动的幅值、频率随时间逐渐变化,单独从时域或频域进行分析会对结果的精度造成影响。智能压实基础理论方面的研究刚刚起步,对振动压实过程中振动波的传播机制仍然不够清楚,大大限制了路基智能压实技术的发展和应用。

基于此,本文以京雄城际铁路固安车站的路基段为试验场地,在填筑碾压过程中分层布设传感器,从时域、频域、时频域及能量4个方面研究振动压实过程中不同深度土层的动力特性以及振动信号自振动轮至填料全过程的传播机制,为后续铁路路基智能压实理论发展提供支撑。

1 现场试验方案

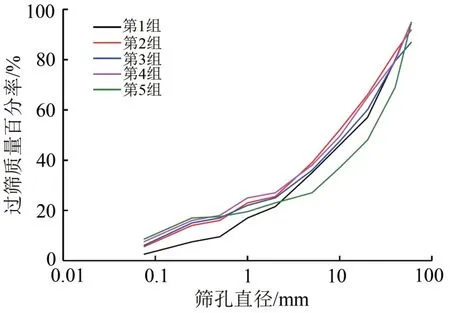
图1 填料颗粒级配曲线

为研究填料压实过程中振动波自振动轮至填料深处的传播机制,本文将拥有大量路基压实工作的京雄城际铁路固安东站作为试验段,选取长200 m、宽100 m 的试验场地。试验段路堤分为20 层自下而上分层填筑压实,每层厚度控制在30 cm 左右,填料为A 组和B 组粗角砾料,在碾压前选取5 组填料试样开展颗粒级配试验,试验结果如图1所示。工作。考虑到现场降雨频繁,为保证传感器的正常运行,需要对传感器进行防水处理,在传感器表面涂上一层酸性玻璃胶将其密封。由于三向加速度传感器对埋设方向具有较高的要求,试验中在三向加速度计的底面黏结了1 块5 cm×5 cm×1 mm 质量较轻、刚度较大的薄板,防止振动压实过程中加速度出现较大的转动。基于前期大量的压实工作,在该段路基填料铺平、静压后,采用弱振更有利于路基的压实。因此,当该层填料铺平、静压后,采用弱振方式进行压实。

试验振动压实设备采用三一重工SSR260C-6型振动压路机,整机质量26.7 t,额定功率180 kW,振动频率为27～31 Hz,振动幅值为1.03～2.05 mm。数据采集设备采用东华测试32 通道动态数据采集设备DH5922D,加速度传感器采用东华测试三向加速度传感器1C302,量程为±5.0g。以边填筑边埋设的方式将传感器布置在振动轮及其下6层填筑层,获取振动过程中振动轮与填料各测点的加速度同步响应数据,测点的具体布置情况如图2所示,其中第6层为本次试验需要压实的填筑层。

图2 测点布置示意图

在传感器埋放之前首先采用万用表等仪器对其进行检测和校正,以保证传感器在试验时能够正常

2 试验结果及分析

为了系统分析振动信号自振动轮至填料深处沿垂向的传播规律,本文将从时域、频域、时频域及能量4个方面展开研究,具体结果分述如下。

2.1 加速度峰值沿垂向传播规律

在振动压路机碾压过程中,为确保采集波形与原始波形的拟合度［9］,本次试验振动轮和各填料层测点加速度采集频率均大于2 000 Hz。填料测点采集到的振动信号时长约为10 s,故选取10 s 的加速度数据进行分析。图3为振动轮与填料各测点垂向加速度峰值变化曲线。

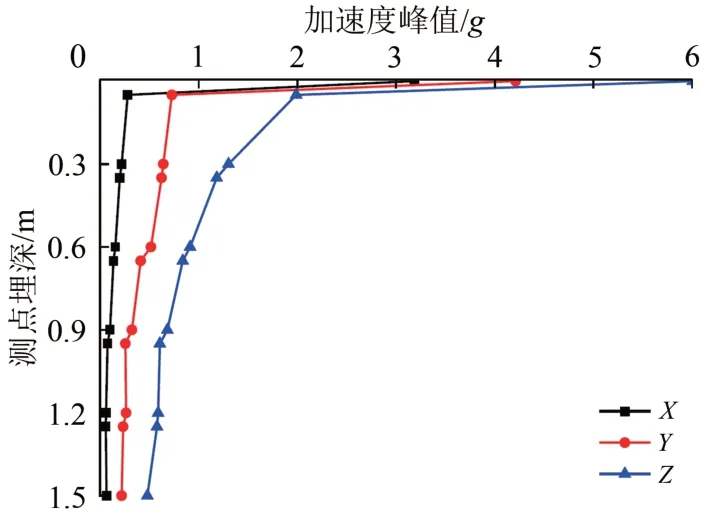
图3 不同方向加速度峰值垂向变化曲线

综合分析图3可知：在振动信号自振动轮至填料深处的传播过程中,振动加速度峰值大致呈双曲线分布,且与埋深呈反向关系。当振动信号从振动轮传播至填料表面,Z,Y和X方向的振动加速度峰值分别衰减了67%,83%和91%；当振动信号从填料表面传播至埋深0.95 m 时,Z,Y和X方向的振动加速度峰值分别衰减了89%,92.3%和97.6%,之后基本稳定；传播至埋深1.50 m 时,峰值分别衰减了92%,95%和98%,振动信号基本上全部衰减。由此可知,在振动压实过程中,振动信号传播的临界深度为1.0 m 左右。同时,在填料分界面处,各方向的振动加速度峰值均呈台阶状,出现上述现象主要是由于填料分层压实造成的各层填料的物理力学参数存在差异,尤其是分界面两侧填料的阻尼、刚度存在差异［10］,进而引起振动信号在分界面处出现大量的反射、透射等现象,减弱了振动信号向下的传播。

为了能够量化分析填料交界面对振动信号传播的影响程度,将每个交界面下方测点的加速度峰值与其上方测点的比值作为加速度峰值衰减百分比,其结果如图4所示。

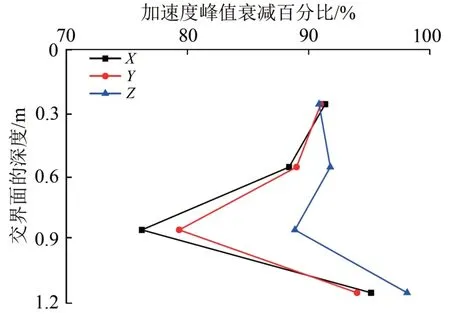
图4 加速度峰值在不同交界面处的衰减

由图4可见：各方向加速度峰值沿垂向的衰减情况基本一致,呈“侧钟”形状,且X方向衰减最大,其次为Y方向,Z方向衰减最小；随着深度的增加,不同界面的衰减百分数逐渐减小,在埋深为0.9 m 时达到最大,仅为75%左右,之后逐渐增大；出现上述现象的原因是振动信号传播至深度大致为1.0 m 左右,在压实过程中会造成该范围内的填料二次碾压,使其密度和刚度逐渐增大,造成分界面两侧填料的物理力学参数差异增大,对振动信号的反射增大,加速度峰值衰减增大。

2.2 加速度频谱特性沿垂向传播规律

大量研究成果表明,填料的压实度指标（CMV［11］和CCV［12］）与振动加速度垂直方向的频谱特性有关。因此,对振动轮及填料各测点的加速度进行傅里叶变换,开展加速度频谱特性沿埋深方向变化规律的研究。振动轮及填料各测点的傅里叶频谱曲线如图5所示。

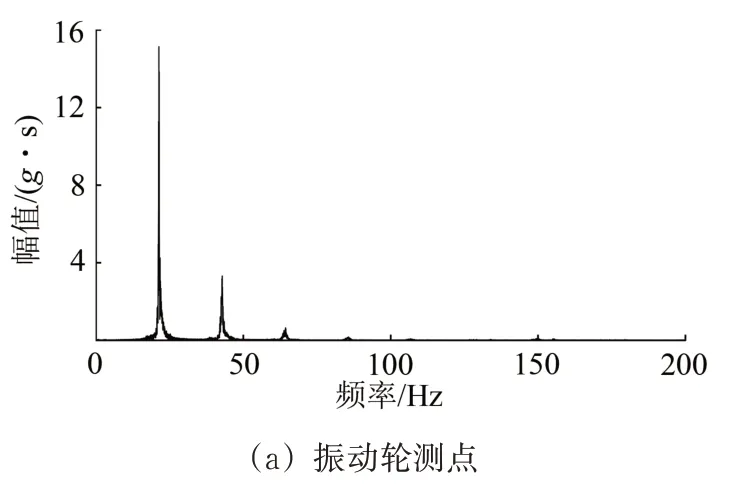
图5 振动轮及填料各测点的傅里叶频谱曲线

由图5可知：振动信号自振动轮至填料的传播过程中,各测点均出现多次谐波现象；振动轮加速度信号的基波频率为21.38 Hz,而填料各测点的基波频率增大至22.00 Hz 附近,各次谐波的频率均为其基波频率的倍数；振动轮振动信号基波与各次谐波的傅里叶幅值明显大于填料各测点,且随着深度逐渐减小,各次谐波幅值与基波幅值的比值却逐渐增大。

图6给出了不同深度基波各次谐波幅值的变化规律。可见基波与各次谐波幅值呈双曲线分布,且与深度呈反向关系；任意埋深处,振动波的基波、1 次、2 次至5 次谐波的幅值呈现指数递减,且具有严格的指数函数相关性,R2=0.9809。

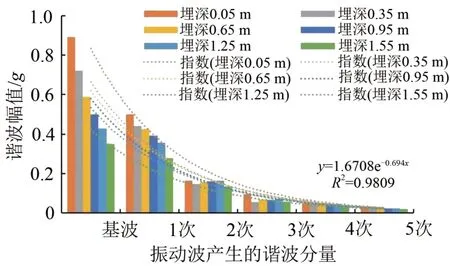
图6 不同深度处各次谐波的幅值

3 基于HHT的振动信号时频域特征

为了全面表述振动信号的演化特征,对实测加速度进行Hilbert-Huang 变换,得到振动轮及填料各测点的Hilbert 谱,分析振动信号在时频域及能量方面的演化特征。

3.1 Hilbert-Huang变换

Hilbert-Huang变换是由Norden E.Huang［13］于1998年提出的一种适用于非线性、非稳定性信号处理的自适应时频分析方法,在海洋、爆破等工程领域应用广泛［14-15］。Hilbert-Huang 变换主要包括EMD 经验模态分解和Hilbert 谱分析2 个部分。EMD 主要利用时间序列上下包络的平均值确定“瞬时平衡位置”,进而提取一系列具有不同特征尺寸的固有模态函数IMF。随后,对分解出来的IMF 分量作Hilbert 变换,可以得到信号在时间—频率—能量尺度上的分布规律,即Hilbert谱函数为

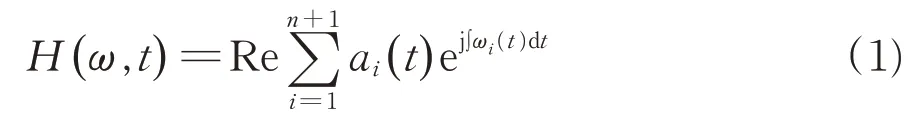
式中：ai（t）为IMF 幅值随时间的函数；ωi（t）为IMF频率随时间的函数；Re表示取实部；n为IMF的数量。

在Hilbert 谱的表达式中对时间进行积分,则可得到信号在频率-幅值尺度上的分布规律,即为对应的边际谱函数

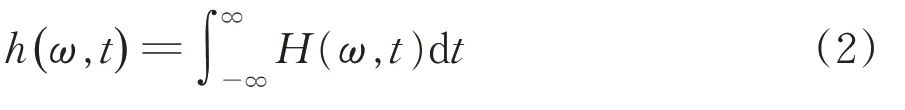
3.2 振动信号的EMD分解

下面以振动轮实测的加速度时程加以说明,首先对振动信号进行EMD 分解,计算得到13个IMF分量和1个残余分量,在此基础上,对每个分量进行Hilbert-Huang 变换,即可获得14 个Hilbert 谱,如图7所示。将每个IMF的Hilbert谱进行合成,即可获得振动信号的Hilbert谱,如图8所示。

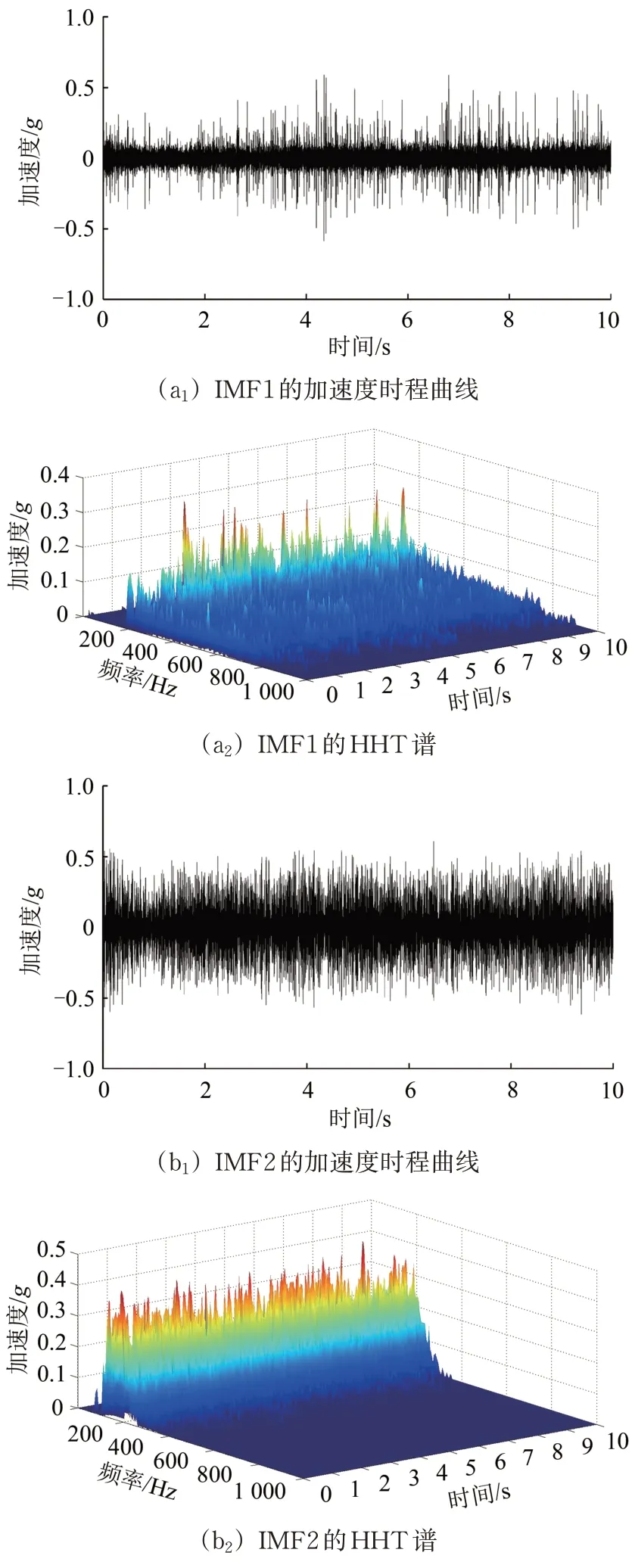
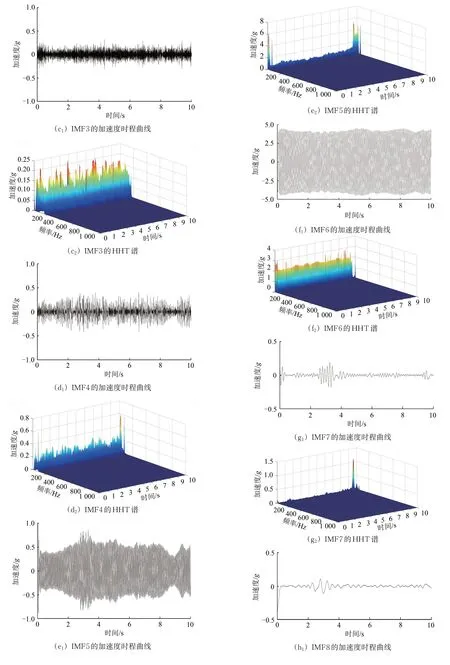
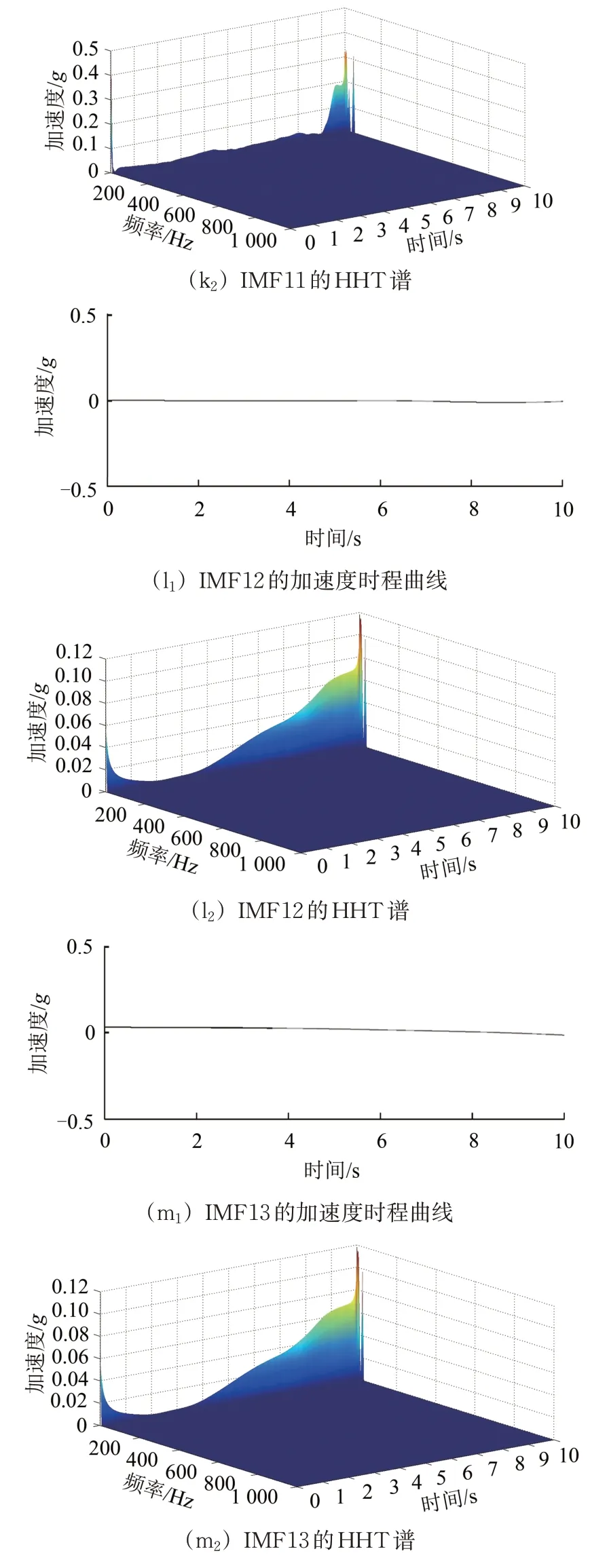
图7 分解后的IMF分量及其Hilbert谱

综合分析图7和图8可知；振动轮上激励信号加速度经过分解后具有不同的振幅和频率成分的IMF 分量,其中IMF6 的幅值最大,且主频率与原始信号的基波频率基本一致；IMF5 主要包含与振动轮1 次谐波相同的频率,IMF4 则包含与原始信号的2 次、3 次谐波相同的频率,其余IMF 分量均为高频或低频信号,幅值较低,所携带的能量小,可能是由于振动压路机自身产生的干扰振动。

图8 振动轮加速度时程曲线及其Hilbert谱

3.3 Hilbert谱沿垂向的演化规律

为了研究Hilbert 谱沿深度方向的演化规律,系统分析12#,10#,8#,6#,4#和2#测点的Hilbert谱,如图9所示。

由图8（b）和图9见：振动轮及各测点振动信号的Hilbert 谱能够全面、系统地反映任意时刻上信号的频谱特征和时域特征；在振动波信号自振动轮至填料的传播过程中,所携带的能量逐渐减小,振动轮测点的振动信号所携带的能量主要集中在10 s 内分布较为平均,对应的频率则在20～50 Hz 之内；填料测点的振动信号所携带的能量则在2～4 s 之间,对应的频率同样在20～50 Hz 之内,说明振动压路机对于填料的有效碾压时间大致为2 s。

图9 填料各测点的Hilbert谱

为了准确表述振动能量沿垂向的传播规律,对振动轮和填料各测点的Hilbert 谱进行时间积分,得到振动轮和填料各测点的边际谱,如图10所示。

综合分析图10可知；振动轮振动能量主要集中在基波所对应的频率附近,在填料中则是出现在基波和1次谐波频率范围内。随着深度的增加,振动信号的边际谱逐渐由单峰值向双峰值过渡,1次谐波所对应的能量占总能量的比值逐渐增大。在振动信号自振动轮至填料的传播过程中,其所携带的能量逐渐减少,特别是振动能量从压路机传至填料表面时,振动能量发生了大量的消耗,传递效率过低,如何能够提升能量传递效率对节能、提高效率至关重要。

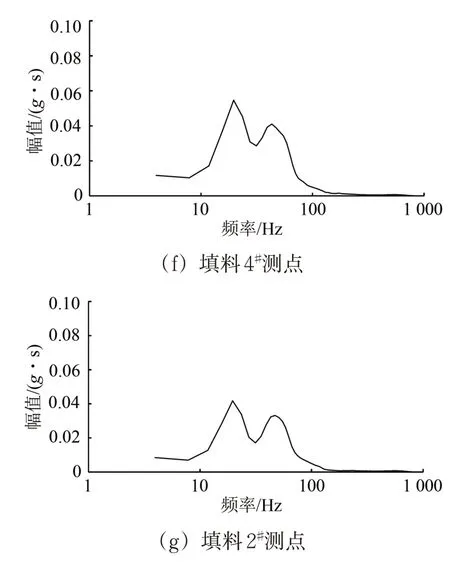
图10 振动能量沿深度的演化

4 结 论

（1）振动信号自振动轮至填料的传播过程中,振动加速度峰值呈双曲线分布,且与埋深呈反向关系,其传播的临界深度为1.0 m 左右。在填料分界面处,受填料物理力学参数差异的影响,不同方向的振动加速度均呈现台阶状。

（2）振动信号自振动轮至填料的传播过程中,产生多次谐波现象。振动信号的基波频率由振动轮的21 Hz 增大至填料的22 Hz,其基波与各次谐波的幅值与埋深呈方向关系。在任意埋深处,振动信号的基波、1 次、2 次至5 次谐波的幅值呈现指数递减,具有严格的指数函数相关性。

（3）振动信号可由EMD 分解为若干与基波、1 次谐波以及2 次谐波等频率对应的IMF 分量。而且通过振动信号的Hilbert 谱可知,振动压路机对于任意填料的有效碾压时间大致为2 s。

（4）在振动信号自振动轮至填料的传播过程中,其所携带的能量随深度的增大逐渐减少,特别是在压路机传至填料表面时,振动能量发生了大量的消耗,而且振动信号的边际谱逐渐也由单峰值分布改变双峰值分布。