考虑IP效应的可控源电磁法电磁响应畸变分析
潘 威
(中铁一院 甘肃铁道综合工程勘察院有限公司,兰州 730000)
0 引言
岩矿石是复杂的多相介质,电阻率、极化率等参数是岩矿石本身的固有物理属性,以激发极化效应理论为基础的频谱激电法,是一种有效的地球物理勘探方法,对此方法国内、外皆有研究[1—9]。可控源电磁法(CSEM)现已广泛应用于油气、矿场等资源勘探中,目前,国内、外学者对CSEM的研究主要只考虑纯电磁感应[10—15],但是当地下介质中含有极化层时,会对CSEM的电磁响应产生影响,而用常规的CSEM理论已无法进行有效解释。因此笔者首先建立不同的三层地电模型(仅考虑中间层极化),将极化参数加入到有限长导线频率域电磁法一维正演中去,对含IP效应、纯电磁感应的Ex、Hy、Hz电磁响应进行理论分析,为含IP效应的人工源频率域测深方法提供一定的理论参考。
1 不同地电模型CSEM一维正演
1.1 CSEM基本理论
设发射导线长度为L,铺设于地表,取坐标原点O,接收点A。如图1所示,图中r为收发距。
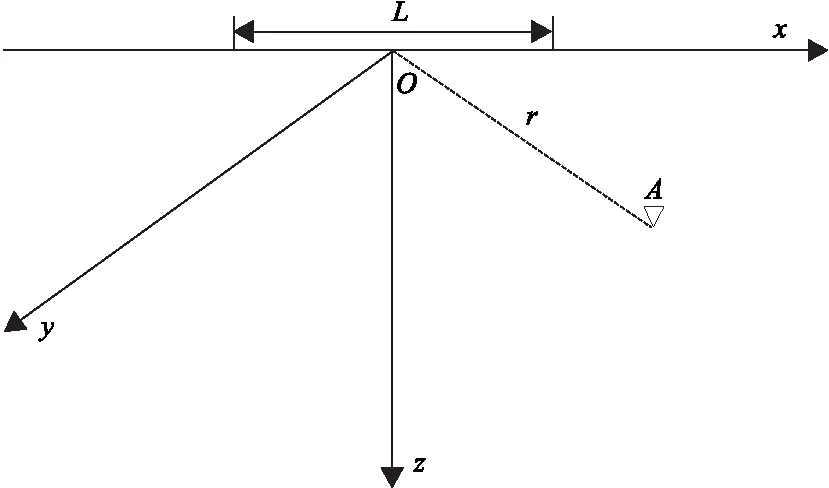
图1 均匀半空间下的有限长导线源示意图Fig.1 Schematic diagram of finite-length traverse source in Geodetic medium
则纯电磁感应的有限长导线源的电场x分量、磁场y分量以及磁场z分量表达式如下:
J1(mr)cos2θ/r]dm
(1)
m2J0(mr)cos2θ]dm
(2)
(3)
(4)
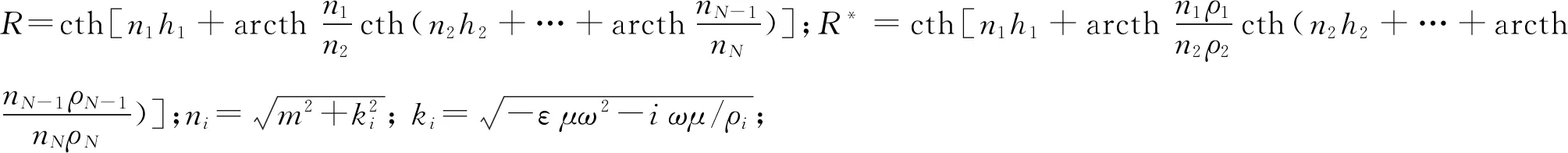
本次测试将设置导线长为2 km,发射点坐标为(0,0),接收点坐标为(5 000,9 000),电流大小为1 A。
1.2 含激电数值模拟
描述岩矿石中的激发极化效应的激电模型有多种,笔者仅对应用最为广泛的Cole-Cole模型进行讨论。
(5)
式中:ω= 2πf为圆频率;ρ(ω)为频率为ω时的岩、矿石复电阻率(Ω · m);ρ0为零频电阻率(Ω ·m);m为极化率;τ为时间常数(s);C为频率相关系数。经过推导[16]可得Cole-Cole模型的振幅表达式为式(6)。
(6)
将式(6)代替式(1)、式(2)、式(3)中的地层电阻率ρ,从而进行含IP效应的可控源频率域一维正演计算,并利用式(7)进行电磁场响应畸变分析。
(7)
式中:|F|为含IP效应的频率域电磁场响应的振幅值;|FB|为纯电磁感应的电磁场响应的振幅值;δ为最大相对异常值或最大相对畸变值。
1.3 均匀半空间正演模拟
为验证本文所用数值算法的正确性,采用均匀半空间情况下的水平电偶极子的电磁场Ex,Hy以及Hz分量解析解表达式:
(8)
式中:PE=Idl,K1、K0、I0、I1表示虚宗量贝塞尔函数。然后计算出纯电磁感应以及考虑IP效应的解析解[16],如图2、图3中虚线所示。均匀半空间地电参数为ρ0= 150 Ω·m,m= 0.5,C= 0.45,τ= 150 s。
在层状介质情况下,式(1)、式(2)、式(3)一般是没有解析解的,因此可采用快速汉克尔变换方法对其进行计算,进而得到各电磁场分量的数值表达式,其具体算法可参考文献[16]。计算数值解时每层的地电参数皆为均匀半空间地电参数。根据图2、图3可知,均匀半空间情况下含IP效应以及纯电磁感应的数值解与解析解在频率10-2Hz ~103Hz 的范围内拟合很好,说明该数值算法的正确性。
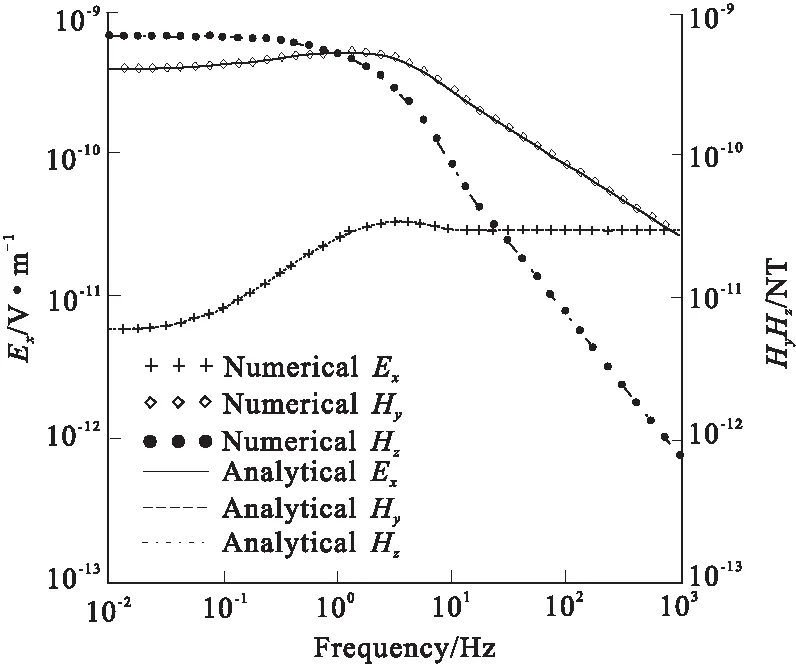
图2 纯电磁感应的数值解与解析解Fig.2 Numerical solution and analytical solution only considering electrical variation
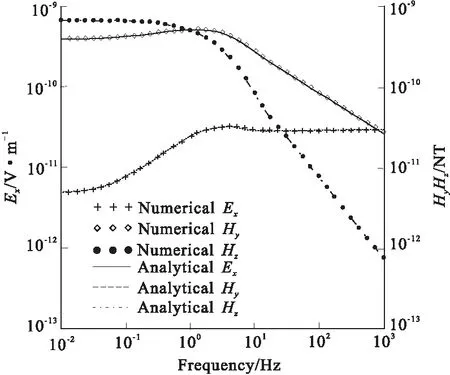
图3 考虑IP效应的数值解与解析解Fig.3 Numerical solution and analytical solution with the IP effect
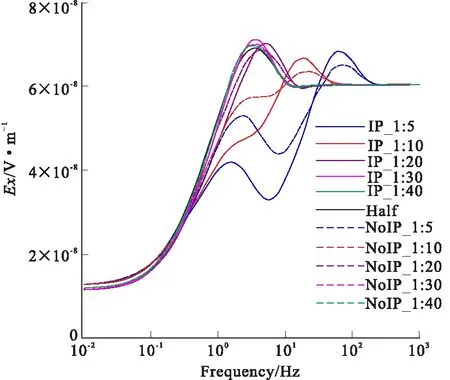
图4 M-200的Ex响应曲线Fig.4 The thickness of 200m of Ex curve
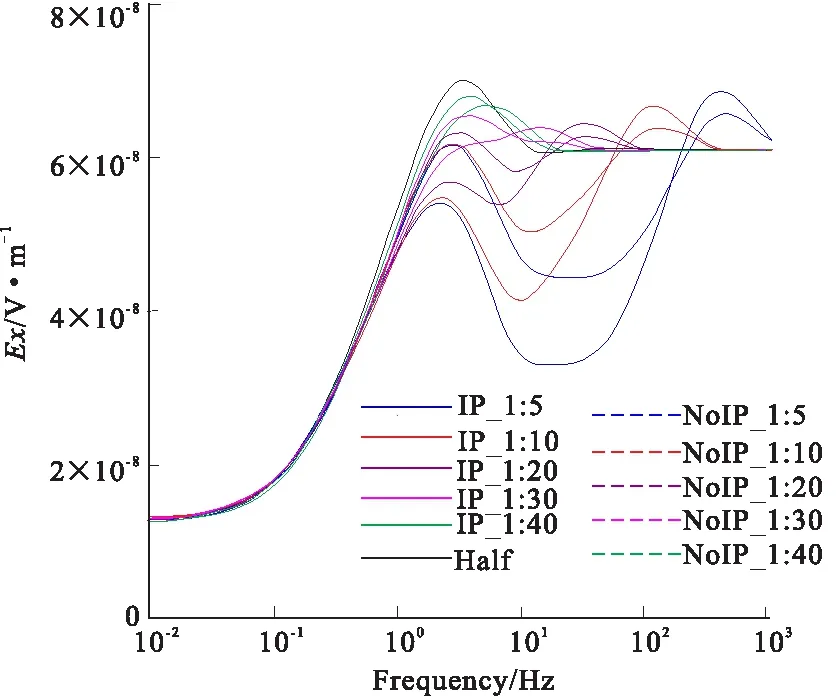
图5 M-80的Ex响应曲线Fig.5 The thickness of 80m of Ex curve
1.4 层状模型正演模拟
为进行含IP效应的三层层状介质模型正演,设置中间层为极化层,层厚分别为200 m、80 m。第一层厚度等于中间层的厚度除以厚度埋深比(极化层的厚度与其埋深的比值),每层极化参数如表1所示。
图4~图9是不同厚度埋深比情况下考虑IP效应和纯电磁感应的一维正演模拟结果。为了进行畸变分析,计算了考虑IP效应和纯电磁感应的最大相对畸变值,见表2、表4;同时也计算了层状介质情况下考虑IP效应的电磁场响应与均匀半空间情况下纯电磁感应的电磁响应的最大相对异常,见表3、表5。
图4、图6、图8为极化层厚度为200 m时电场分量Ex,磁场分Hz响应曲线。对比纯电磁感应的响应曲线,加入激电效应后的响应曲线形态有所改变,水平磁场Hy以及垂直磁场Hz幅值的极大值与极小值之间的差值变大,这是由于极化层的电阻率随频率的变化发生改变,而随着厚度埋深比的减小以及电磁波传播距离的增加,响应畸变出现在更低的频率处。当厚度埋深比达1:10时,根据表2可知,由激电效应引起的响应畸变逐渐减小。如表3所示,根据最大相对异常值可知,Hz对浅部极化层更为灵敏,其次是电场分量Ex,而水平磁场Hy最弱。对比于其他分量,Ex对深部极化层依然有一定的反映能力。
图5、图7、图9表示目标层厚度为80 m时电磁场各场值的理论响应曲线。同样随着埋深的加深,激电效应对电磁场分量的幅值的影响减弱。根据表4,当厚度埋深比为1:20时,考虑IP效应的响应与纯电磁感应的响应之间的差别减小。
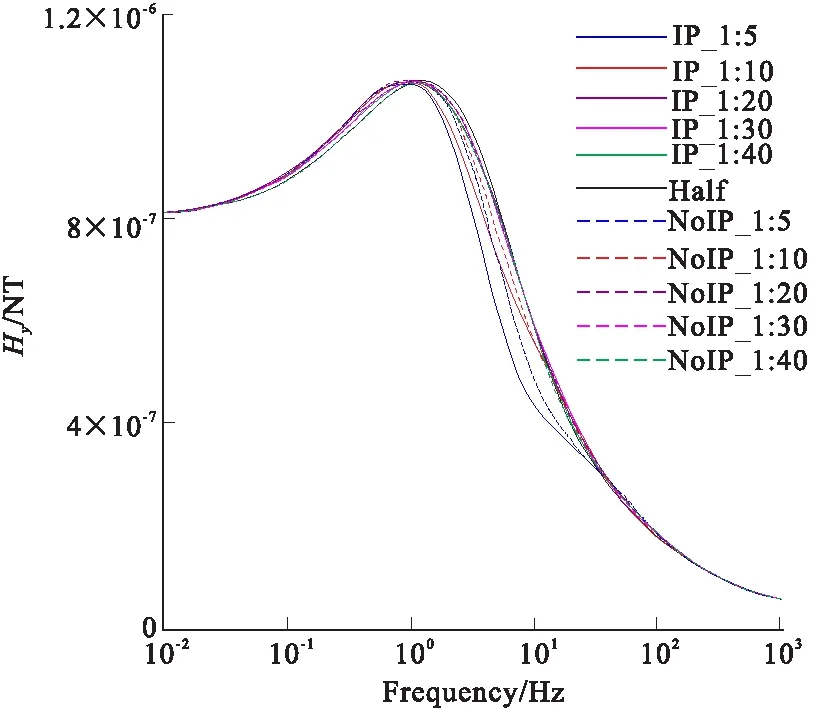
图6 M-200的Hy响应曲线Fig.6 The thickness of 200m of Hy curve
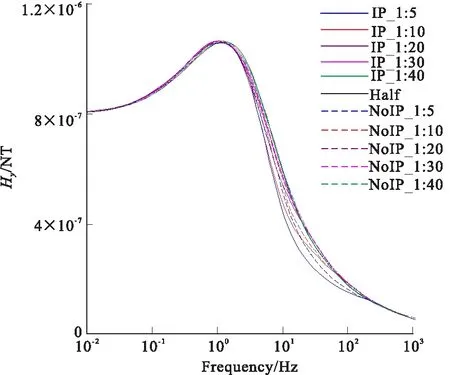
图7 M-80的Hy响应曲线Fig.7 The thickness of 80m of Hy curve
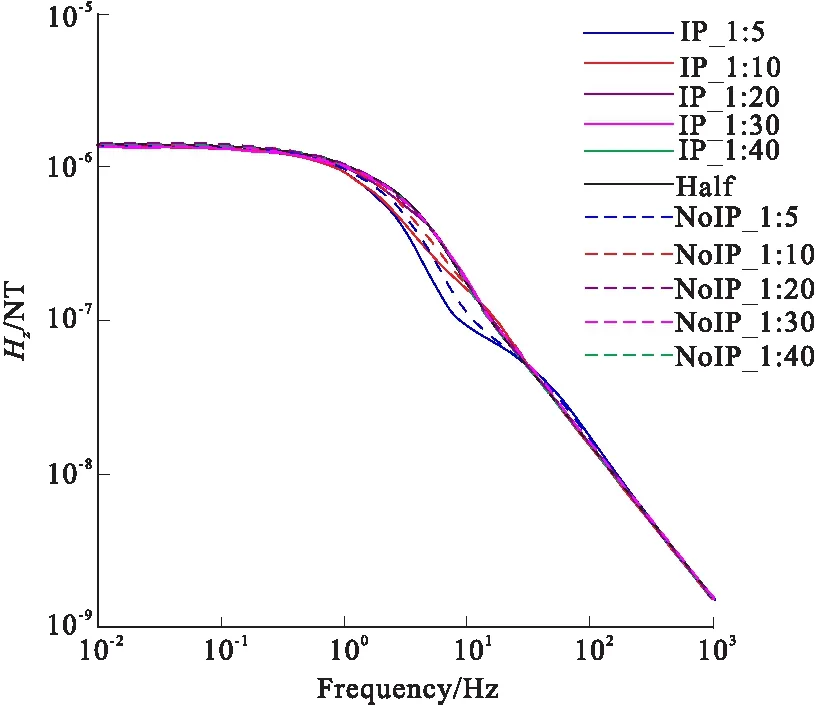
图8 M-200的Hz响应曲线Fig.8 The thickness of 200m of Hz curve
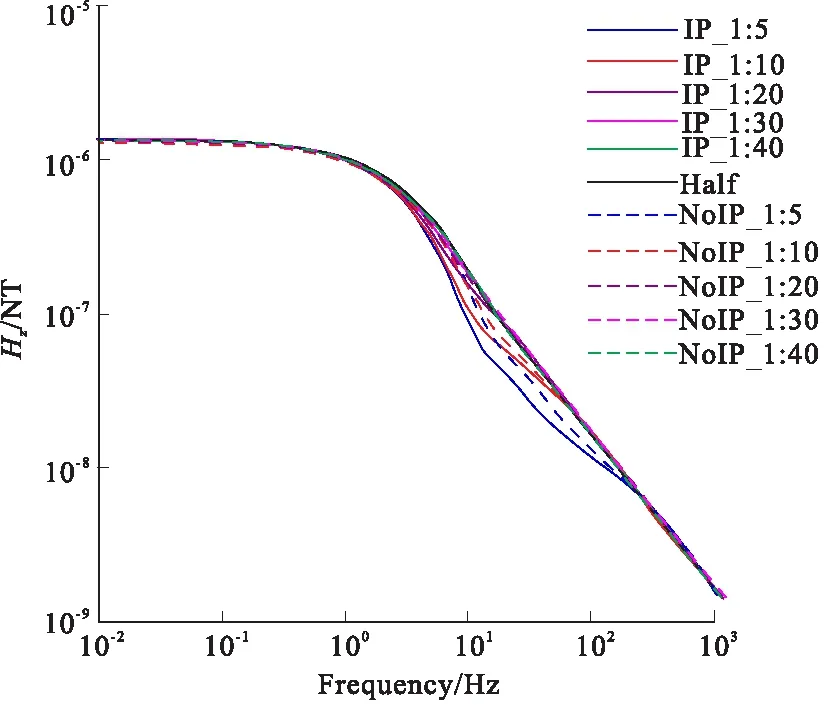
图9 M-80的Hz响应曲线Fig.9 Thickness of 80m of Hz curv

表1 三层地电模型参数表
综上所述,在考虑IP效应的情况下,根据不同层厚所对应的地电模型的理论响应,分析可知随着厚度埋深比的减小,激电效应所引起的响应畸变出现在更低的频率处并减弱, 同时根据表3、式5可知,电场Ex及Hz对极化层的反映更为灵敏,Hy则最弱。
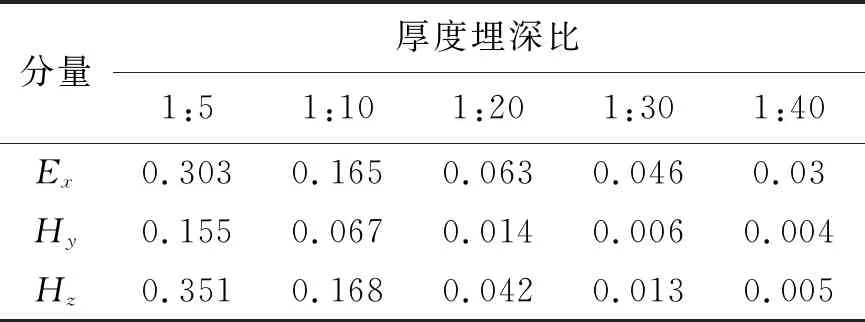
表2 极化层层厚为200 m时电磁场各分量最大相对畸变值
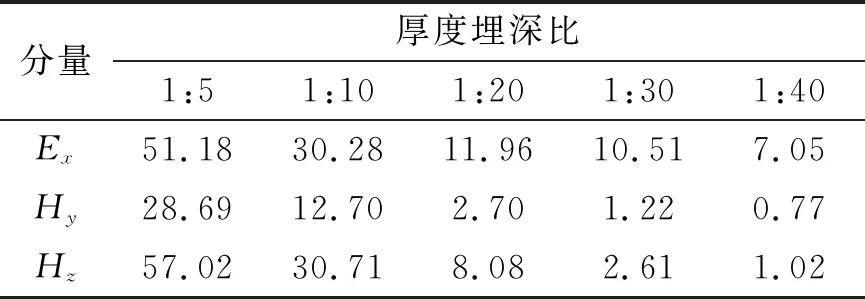
表3 极化层层厚为200 m时最大相对异常
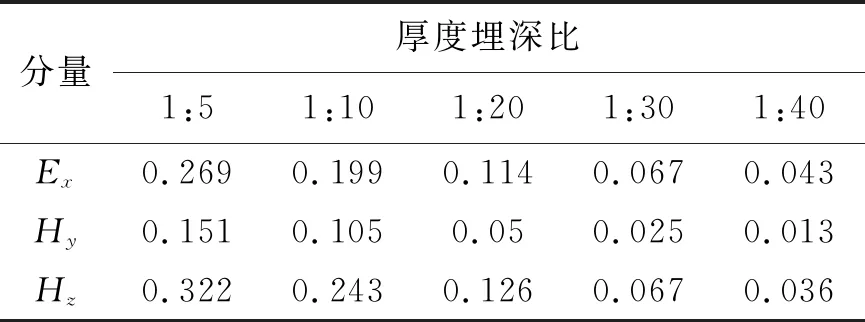
表4 极化层层厚为80 m时电磁场各分量最大相对畸变值
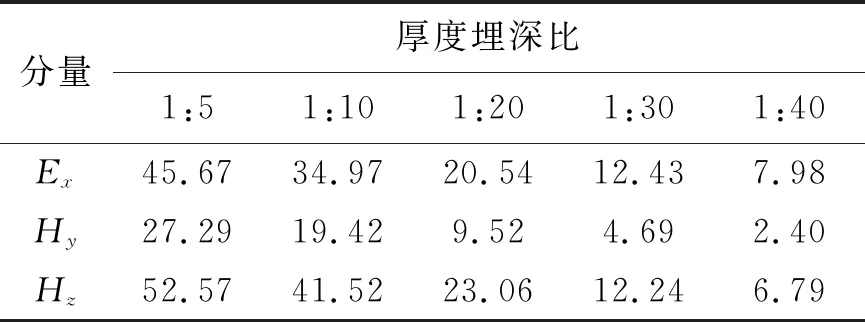
表5 极化层层厚为80 m时最大相对异常
2 结论
通过典型三层模型模拟计算得到以下结论:
1)在CSEM数据解释中,地层的IP效应造成的响应畸变往往是不能忽略的。根据本文的模拟结果,几个特定模型相对畸变最大可达到30%,随着埋深的增加,受IP效应的影响减弱。
2)对于本文的算例而言,对比电磁场各分量极化最大异常值,Hz受IP效应的影响较大,其次是电场分量Ex,Hy最弱。

