基于CMP域的山地表层速度模型构建
彭 文, 赵 尧, 曹中林, 张 亨, 张 华
(中国石油东方地球物理公司 物探技术研究中心,成都 610213)
0 引言
对直射线路径而言,走时的Abel变换是一维球对称介质的层析算法。Herglotz-Wiechert公式可通过Abel变换用精确的射线轨迹推导出来。在一定条件下(如无低速夹层),该公式可应用于弯曲射线,并能提供一种直接计算地层速度-深度函数的方法[1],此公式通常用于天然地震学中。对石油勘探而言,在多数情况下近地表可以被假设成为一种速度随深度增加而增大的结构。一些研究人员把Herglotz-Wiechert公式应用于近地表反演中,例如:Gelius用Chebychev多项式通过最小平方法拟合折射波初至旅行时,然后利用Herglotz-Wiechert公式计算随深度变化的速度函数[2];Osypov[3-4]提出了一种根据Herglotz-Wiechert公式应用走时曲线做折射层析的新算法,该算法不需具体的射线追踪,不需初始模型。
在已提出的应用Herglotz-Wiechert公式反演近地表的方法中,常常忽略地形起伏,而且主要是用炮集数据进行处理。然而在山地地震勘探中地形起伏,不满足该积分公式要求的水平地表假设。在起伏地表中,回转波走时-偏移距曲线的斜率(视慢度)难以精确表示回转点的瞬时慢度(射线参数)。炮集由一个炮点和一组不同的检波点构成,与不同检波点对应的回转波射线的回转点位置在水平面上并不集中于一点,而是分布在一个区域内。因此,基于炮集的方法实际上是在一个排列范围长度上求平均值,这样在复杂近地表地质情况下,就没有足够的分辨率。此外,炮集数据反演结果的水平分辨率取决于炮点的间距,有时显得稀疏。胡自多等[5]为了在山地采集的炮集数据上应用Herglotz-Wiechert公式提出了一个基于起伏地表回转波走时-偏移距方程的走时校正方法。
CMP分选域被认为是代表了地下一点的结构,基于反射波的这种假设也同样适用于折射初至波的地表一致性表示。但与反射法不同的是同一个CMP道集中不同偏移距的每个炮检对提供了地下不同部分的信息,即不同的深度对应各自的速度[6]。张建中等[7]利用CMP道集的初至走时-偏移距方程通过剥层法来估计近地表的一维速度模型。回转波的回转点位于CMP点的正下方,可通过基于CMP域的初至波走时-偏移距曲线利用Herglotz-Wiechert公式反演速度-深度函数。
笔者提出了一组基于CMP浮动基准面对起伏地表上的炮检对走时和偏移距进行校正的公式,此方法与胡自多等[5]提出的炮域处理方法的显著区别是在CMP域处理,所有回转波射线的回转点都位于CMP点的正下方,参与反演同一个一维表层速度结构的所有炮点、检波点被校正到相同的水平面上,满足Herglotz-Wiechert公式的要求,由一维速度-深度函数可构建出整个地形起伏工区的三维近地表速度模型,模型的水平分辨率取决于CMP点的间距。
1 方法原理
在地震波速度随深度增加而增大的山地近地表中,一个炮检对的回转波射线轨迹呈圆弧形。对于水平地表,射线回转点的深度可通过Herglotz-Wiechert公式反演得到唯一解,该公式在笛卡尔坐标系中的形式如下[8]:
(1)
其中:xf为在地面出射点f对应回转波的偏移距;Z(xf)为该回转波穿透的最大深度;pf和p分别为偏移距为xf、x的回转波的射线参数。只要由回转波初至走时-偏移距曲线求得连续的射线参数曲线,就可以反演出一维的地下介质速度分布。在一个CMP道集中,所有炮检对的初至波拾取时间构成了一条走时-距离曲线。对于地形起伏的山地地震数据而言,炮点、检波点不在同一个水平面上,那么首先需要对每个炮检对的走时和偏移距进行从起伏地表到CMP浮点基准面的校正。因此,本文提出的方法分为四个主要的步骤。

图1 回转波的CMP浮动基准面校正方法原理图Fig.1 Schematic of the CMP floating datum corrections of diving waves
1.1 产生CMP浮动基准面
建立地震采集观测系统后,用地表CMP点附近一定距离范围内的炮点、检波点高程平均值计算CMP浮动基准面。
1.2 实测时距曲线的校正
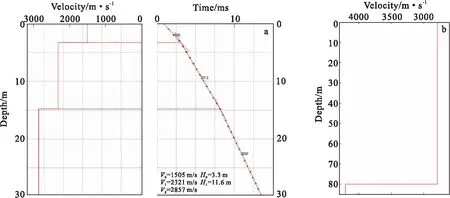
设一个CMP道集由N个地震道组成,有N个炮检对的偏移距x1 (2) 其中:ERi和EM分别为检波点和CMP浮动面的高程;Vw为射线在表层低速带中传播的平均速度,可以用直达波的初至求得。 同时,检波点Ri相应的走时校正量为式(3)与式(4)。 ΔtRi=(ΔxRi)/Vh (3) (4) 其中:Vh为低速带中回转波的水平方向视速度。因此,检波点从地表移到CMP浮动面上引起的走时校正量为式(5)。 (5) 同理,把炮点移到CMP浮动面上引起的偏移距改变量为式(6)。 (6) 炮点相应的走时校正量为式(7)。 (7) 其中:h是炮井深度;回转波射线参数p可用射线在地表出射点处时距曲线的中心差分斜率近似表示,即 (8) 因此,第i个炮检对作CMP浮动面校正后的走时与偏移距为式(9)。 tci=t0i-ΔtSi-ΔtRi xci=x0i-ΔxSi-ΔxRi (9) 式(9)意味着一个CMP道集中所有的炮点、检波点都被移动到了一个相同的水平面上,地形起伏对初至波走时和偏移距的影响被消除掉了,CMP道集中所有被校正过的炮检对初至波走时和偏移距构成了修正的实测时距曲线。通过对川东高陡构造地震资料的实际处理效果表明,式(5)、式(7)计算的检波点和炮点走时校正量能把一个CMP道集中地形高程差在2 000 m范围内的炮点、检波点移动到了一个相同的水平面上。 一个CMP道集中炮检对的偏移距常常呈非均匀分布和某些范围的偏移距缺失的情况,因此,需要用某种平滑插值方法对修正后的实测时距曲线作处理,以求得一条光滑连续的时距曲线,尽量消除随机误差,提高数据的可靠性。用于时距曲线平滑方法较多,经对比表明,三次样条函数平滑法较好,理论严密,并具有良好的平滑性能,插值平滑后的时距曲线应该通过坐标原点。偏移距为xf的回转波射线在地表出射点处的射线参数pf等于时距曲线在该处的一阶导数,即 (10) 射线参数为pf、偏移距为xf的回转波在回转点处的射线入射角为90°。根据Snell定理,该射线在回转点处的瞬时速度为 Vf=1/pf (11) 另一方面,通过式(1)可得到偏移距xf对应的回转波的回转点深度Z(xf),此深度既是回转波的最大穿透深度,也是产生首波的折射层深度,此深度处的回转波速度为Vf,当xf=0,Z(0)=0。 在初至时距曲线上取一系列的偏移距xf1 利用在四川盆地大川中地区采集的一条炸药震源2-D测线地震数据对上述方法进行了试验,炮点距100 m,每炮600道,偏移距范围是10 m~5 999 m,道距20 m, CMP点间距10 m,60次覆盖。图2(a)展示了一个具有59道的CMP道集初至。从图2可见,在道集内每个地震道代表的炮检对偏移距呈不均匀分布,从图2(b)也可看到,CMP道集内的炮点、检波点高程分布于300 m~500 m范围内,同一个炮检对中炮点与检波点的高程有的相差较小,有的相差约150 m。 图2 一个CMP道集Fig.2 The CMP gather(a)初至;(b)每个炮检对中炮点和检波点的高程 图3 一个CMP道集的时距曲线Fig.3 The traveltime-distance curve of a CMP gather 图3展示的实测时距曲线(红线),由于起伏地表的影响,呈现曲折拐弯的形态,经CMP基准面校正和插值平滑后变成了一条光滑连续的曲线(蓝线),此时所有的炮点和检波点都位于同一个水平面上,满足Herglotz-Wiechert公式的应用条件。比较图4(a)所示微测井测量结果与图4(b)所示本文方法的反演结果可见,微测井清楚地刻画了在0 m~15 m深度范围内表层低速带速度从1 000 m/s到3 000 m/s范围之间的变化情况,而本文方法未能反映出这种情况,两者对于大于15 m深度的降速带速度值基本一致(2 787 m/s~2 857 m/s),微测井由于成本原因没有打穿降速带,而本文方法从初至波反演出了高速层顶界(速度大于4 000 m/s的界面)的埋深为80 m。 图4 CMP道集的一维近地表速度模型Fig.4 The 1-D near-surface velocity model corresponding to one CMP gather(a)微测井测量结果;(b)反演得到的近地表速度模型 山地由于地形起伏变化,不能直接使用Herglotz-Wiechert公式。笔者采取与胡自多等[5]提出的炮域处理不同的CMP域处理思路,基于CMP域,首先去除起伏地表对初至波的影响,然后才应用Herglotz-Wiechert 公式反演。该算法对于二维、三维的处理方法一致,对山地近地表速度模型的反演结果是有效的,但是通过对川东高陡构造地震资料的处理实践表明,当一个CMP道集中炮点、检波点高程差大于2 000 m时,根据本文公式计算出的炮点、检波点走时校正量误差较大。同时,通过与微测井的成果对比,我们发现Herglotz-Wiechert公式反演结果在近地表结构的浅层误差大,中深层的误差小。面波反演表层结构的结果是浅层的误差小,而对深层的探测能力不足。因此,可以把两者的反演结果组合起来形成一个浅中深层误差都比较小的近地表速度模型,并作为旅行时层析反演或全波形反演的初始模型。1.3 计算射线参数
1.4 求速度-深度函数
2 实例


3 结论

