矩形波下斜支承系统关键件的动力学特性

段宁宁，林渊智

（福建技术师范学院 a.海洋与生化工程学院；b.食品软塑包装技术福建省高校工程研究中心,福建福清 350300）

斜支承缓冲减振包装系统目前在现代汽车领域得到广泛应用.正是由于该结构具有优良的减振性能,因此将其引入并应用到缓冲包装领域.根据文献[1]研究发现,为增加对产品的保护效果,将弹簧倾斜一定角度比竖直安装更好,因此对斜支承缓冲包装系统的研究也就应运而生.针对斜支承系统的振动特性,一些学者研究了相关参量对系统的影响[2-4].针对系统在典型波作用下的冲击特性,一些学者探究了相关参量对系统的影响[5-7].针对系统的跌落冲击特性,一些学者探究了相关参量对系统关键部件的跌落破损影响[8-9].目前,学者们针对斜支承系统的研究未提及矩形波作用下系统关键件的二维冲击谱,对系统的冲击特性研究不充分,仍存在不足.故而,本文对系统在矩形波作用下的关键件二维冲击谱作进一步阐述.对被保护的精密仪器设备而言,如汽车发动机等,其内部的零部件与主体连接形式多样,力学性能各不相同,内部零部件受力变化与传递到该零部件上的加速度密切相关,当某零部件受力超过许可值时,将失去原有性能而不能正常工作,将这样的零部件定义为关键部件.因此,振动或冲击作用下斜支承减振系统关键部件动力学特性分析十分必要.

本文主要研究当斜支承缓冲减振系统受矩形波冲击时,其关键部件动力学特性的影响因素.参考文献[10-12]中动力学特性分析方法,根据斜支承系统的简化模型,首先利用Ronge-Kutta数值分析法,建立系统受矩形波作用下的非线性方程,然后将关键部件最大加速度与脉冲激励幅值比值作为系统的动力学放大因子,探讨相关状态参量对系统关键部件动力学特性的影响.

1 系统动力学方程的无量纲化

图1（a）所示为一款关于茶杯的斜支承缓冲包装系统实例,图1（b）对斜支承缓冲减振系统力学模型进行简化.

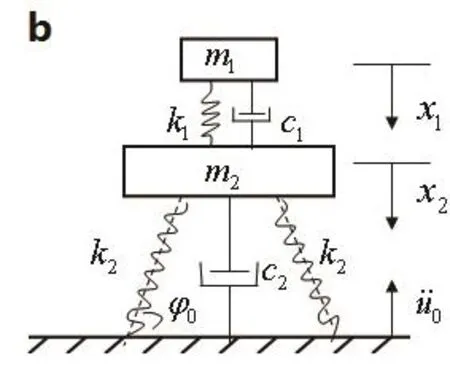
图1 斜支承缓冲包装系统

记：m1、m2为关键部件和系统主体的质量,系统主体与关键部件间的参量为k1（弹性系数）、c1（阻尼系数）,系统主体的相关参量为k2（弹性系数）、l0（弹簧原长）及c2（阻尼系数）,设弹簧在静平衡下的支承角为.矩形波的脉冲数学表达式如下

式中, t0为脉冲激励持续时间.假设竖直向下的方向为正方向,将系统受力平衡位置作为初始位置,根据牛顿第二定律,对上述系统做力学分析并简化[13],如式(2)所示.

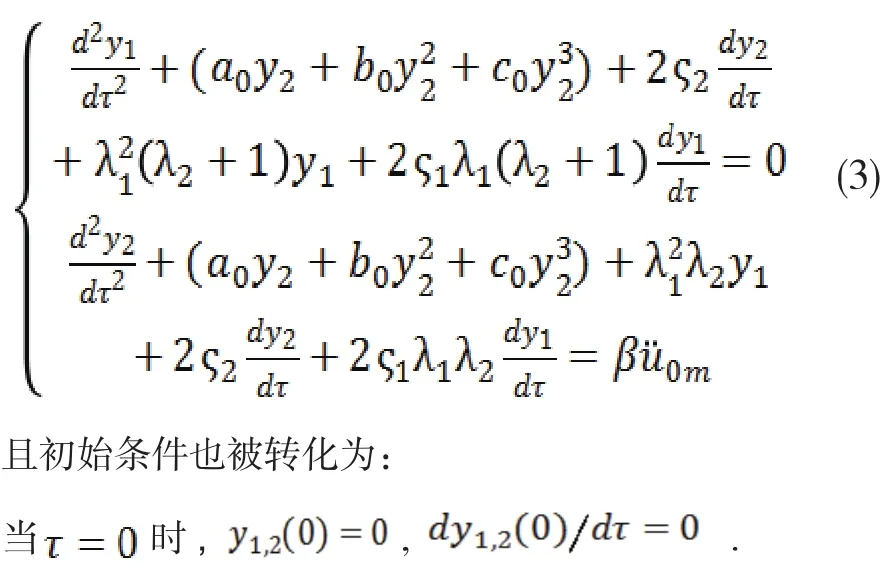
通过对式(3)分析发现,系统在矩形波作用下的动力学响应特性与系统倾斜角度、质量比、系统主体阻尼比等状态参量有关.

2 系统关键件动力学特性分析

2.1 系统关键件二维冲击谱

采用Runge-Kutta法对动力学方程(3)进行求解,探讨关键部件动力学特性及影响因素.

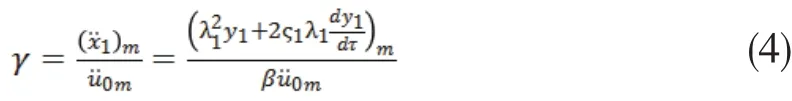
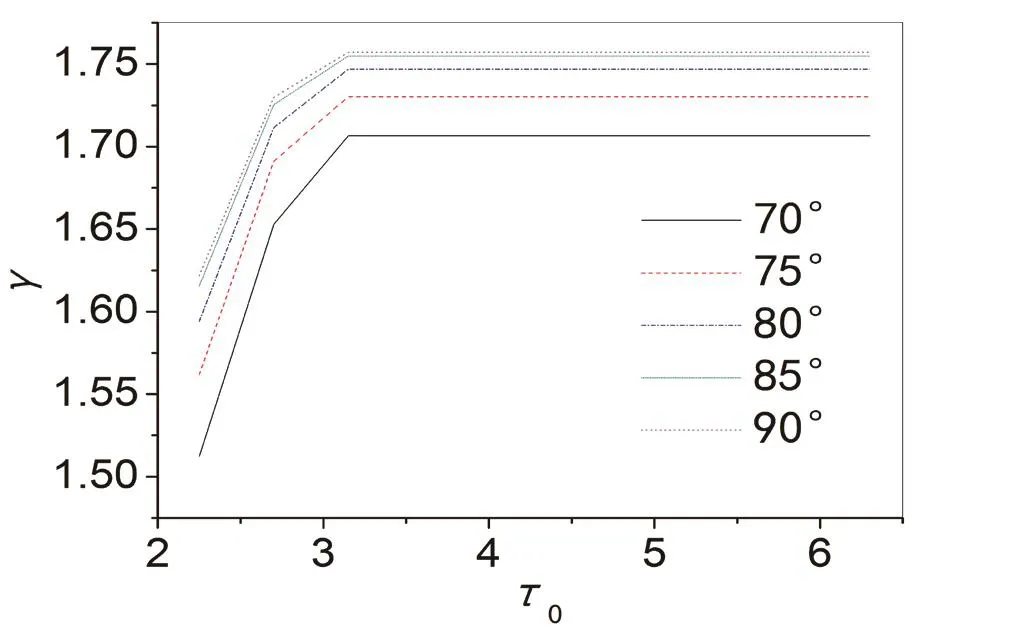
图2倾斜角度对关键部件冲击响应谱的影响（λ2=0.01, λ1=10，=0.05,=0.1,=0.01）

图3 频率比对关键部件冲击响应谱的影响

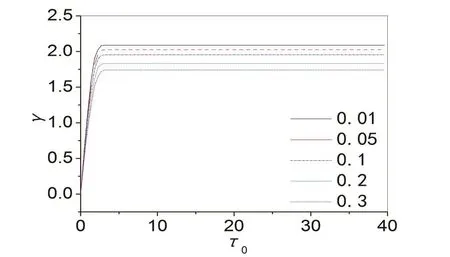
图4 质量比对关键部件冲击响应谱的影响

根据图3所示,与高频率比相对,低频率比对系统关键件冲击响应谱的影响较大,故主要研究低频率比下质量比对关键件冲击响应谱的影响规律（取= 2）.图4所示,设定=70°,= 0.1,= 2,= 0.05,= 0.1,得到不同质量比（= 0.01,0.05,0.10,0.20,0.30）关键部件冲击响应谱.由图4所示,在低频率比（＜ 5）条件下,质量比增大使系统动力学放大因子明显下移,即关键部件最大加速度随质量比的增加发生显著减小.

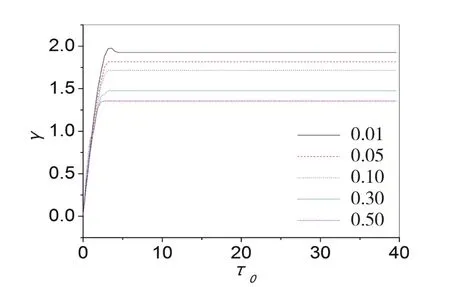
图5 系统主体阻尼比对关键部件冲击响应谱的影响

图6 无量纲脉冲激励幅值对关键件冲击响应谱的影响

2.2 分析与讨论

2.2.1 根据图2所示,当质量比等参数一定时,改变倾斜角度,关键部件的最大加速度随倾斜角度的减小向下移动.有别于常用的线性系统（= 90°）,弹簧只要在一定倾斜角度（70°≤＜90°）内,倾斜角度越小,则关键部件最大加速度越小；

2.2.2 根据图3所示,当阻尼比等参量确定而系统频率比增大时,关键部件的最大加速度出现明显下移.由于关键部件的动力学特性对频率比极其敏感,所以该参量增加,关键部件最大加速度出现显著降低,故而在缓冲包装结构设计过程中,如果条件被允许的情况下应当尽可能地增大系统频率比（建议＞ 5）,对系统关键部件的抗冲击特性具有指导价值；

2.2.3 根据图4所示, 当倾斜角度等参量不变且设定频率比小于5时,关键部件的最大加速度随质量比的增加显著向下移动.即,低频率比范围内,质量比的增大可有效抑制关键部件最大加速度；

2.2.4 根据图5所示,当无量纲脉冲激励幅值等参量固定而系统主体阻尼比变大时,关键部件最大加速度下移明显.即,随系统主体阻尼比的增加,系统关键部件的最大加速度显著降低；2.2.5 根据图6所示,当系统主体阻尼比等参量不变时,关键部件的最大加速度随无量纲脉冲激励幅值增加略有下移.即为,无量纲脉冲激励幅值的加大,使得关键部件最大加速度减小,故而当脉冲激励幅值一定时,增加系统特征参数可改善斜支承减振系统的抗冲击特性.

3 结论

数值结果显示,支承角、质量比、频率比、系统主体阻尼比等对关键部件加速度响应幅值影响显著.结果表明：减小支承角、频率比增加、低频率比下增大质量比等可有效抑制关键部件最大加速度；随系统主体阻尼比变大,关键部件最大加速度随之显著变大.