空间运动的异面转换在机构维度变换和创新设计中的应用
徐晨,林松,王瀚超,范意中
空间运动的异面转换在机构维度变换和创新设计中的应用
徐晨1,林松*,2,王瀚超2,范意中3
(1.同济大学中德学院,上海 201804;2.同济大学 机械与能源工程学院,上海 201804;3.舍弗勒贸易(上海)有限公司,上海 201805)
在使用机构实现异面运动的传递时,为了规避空间机构由于自身特性带来的技术难题,本文探索了用平面机构来实现异面运动传递的新的可能性。通过空间输入输出运动的异面分解和重组,系统研究异面运动在运动几何学意义上的几何关联,借助这种关联的等效几何元素,建立起异面中各平面机构之间的运动联接,提出了实现异面传动的机构设计方法,并将此方法应用于“高速往复模盒铝箔纸折叠机构”的创新设计中,通过异面机构的重组实现空间运动的传递。
异面运动;异面运动几何关联;机构维度变换;传动机构
在机构设计中,使用空间机构传递异面运动。与平面机构相比,空间机构具有运动形式多变、工作灵活等特点[1],在航空航天、工业制造、农业机械、纺织轻工业等领域有着广泛的应用[2],它的设计一直是机构学研究的热点。在空间机构的综合设计上,主要包含型综合和尺度综合[3]。尽管空间机构较平面机构提供了更多运动可能性,但也带来了诸多技术问题。首先在机构的拓扑结构分析方面,由于空间运动副的构型多变,它们的相互布置比平面机构有更多的可能性,因而所组成的空间机构种类繁多,使得求解拓扑结构的自由度也较为复杂;在机构的运动综合方面,空间机构各构件之间的相对运动描述比平面机构更为复杂,大大增加了空间机构综合的难度;在机构的运动分析方面,对空间机构有更多的建模方法,如矩阵法、对偶数法、四元数法及其改进算法等,参数的导出计算不易理解,所得解析式形式相对不直观,很难区别出运动传递的关键环节;在机构的动力学分析和设计方面,空间机构的惯性力和惯性力矩比平面机构更加难以平衡,这些都增加了空间机构设计和分析的难度。
针对这些问题,多年来学者们展开了大量研究,致力于改善空间机构特性。
在自由度计算方面,卢文娟等[4]以自由度计算的核心问题“过约束”为线索,总结具有代表性的多种自由度公式,并提出具有通用性、实用性的自由度新理论。罗建果等[5]提出一种新的构件关系拓扑图论描述方法,给出了一般机构的空间运动能力、自由度的求解方法。
在机构的综合方法方面,袁佩瑶等[6]针对空间连杆机构综合问题,提出了一种基于二平面投影系统和运动反转法的几何法,能够适应多种机构的应用需求。褚金奎等[7]借助傅里叶级数理论,建立由平面机构到空间机构的连杆机构轨迹综合理论,为连杆机构轨迹综合提供了一种有效的通用方法。张英[8]针对刚体导引的全部实数解求解问题,提出通过代数消元,获得一元高次方程,然后再基于施图姆定理求其全部实数解的方法,提供新的研究思路。
在运动学建模方面,廖啟征[9]把齐次坐标变换矩阵分解为哈密顿算符,进而得到其对应的倍四元数形式,为倍四元数的建模与应用提供方便。庄森等[10]以空间连杆机构的对称性为出发点,重建用于求解过程的直角坐标系,有利于机构运动学本质特征的把握。段秀敏等[11]通过类复向量的旋转实现坐标变换过程,利用其性质取代等同条件或约束方程,明显简化计算过程。
在动力学性能优化方面,Murthy等[12]通过生成表面法对空间机构进行运动学分析,提供评估惯性力的依据。Chaudhary等[13]提出了一种新的优化技术,采用七个质点的等矩系统来表示连杆的惯性特性并确定优化变量,平衡空间机构中惯性力。崔东[14]针对空间RSSR机构惯性问题,引入主动平衡方法研究,改善了空间机构动力性能。
由此可见,在空间机构的这些分析和综合方面,学者们一直在努力改善所存在的瓶颈问题,但由于空间机构结构上的特殊性和复杂性,上述问题的解决还有待进一步研究。作为一个新的尝试,考虑到有关平面机构的组成分析、运动分析、精度分析、力分析及平面机构的综合理论研究已相对比较成熟,本文提出在实现预期空间运动的条件下,用平面机构的组合来实现空间运动传递的设计理念,使其不再局限于仅使用空间机构来实现复杂运动任务,而是利用平面构件组或简单平面机构的组合来实现异面运动的传递。本文将以“高速往复模盒铝箔纸折叠机构”的创新设计为例,应用此方法解决实际工程问题,在运动构件的空间布置上体现出更大的简单化、灵活性和可行性,在传递异面运动的设计任务方面,为设计者提供一种新思路和新途径。整体研究内容如图1所示。
1 异面运动相互关联的运动几何学条件
机构可用以传递或转换任何类型的运动和动力,平面机构的所有运动构件上各点的平面轨迹均平行于同一个平面[15]。也就是说,平面机构作为传递运动的装置,能够将其输入运动通过传动构件转换为所需的输出运动,且在运动过程中所有活动构件的运动均保持在相互平行的平面内。在一般空间运动传递中,主动件和从动件都有各自的运动平面,这些平面相互之间在一般的情况下都不平行,这种空间运动的运动关系亦可称为异面运动。当利用常见的空间机构来传递异面运动时,空间机构中某些活动构件的运动必须脱离输入运动平面(记为π)或输出运动平面(记为π),才能将输入运动转换为与其异面的输出运动平面上。
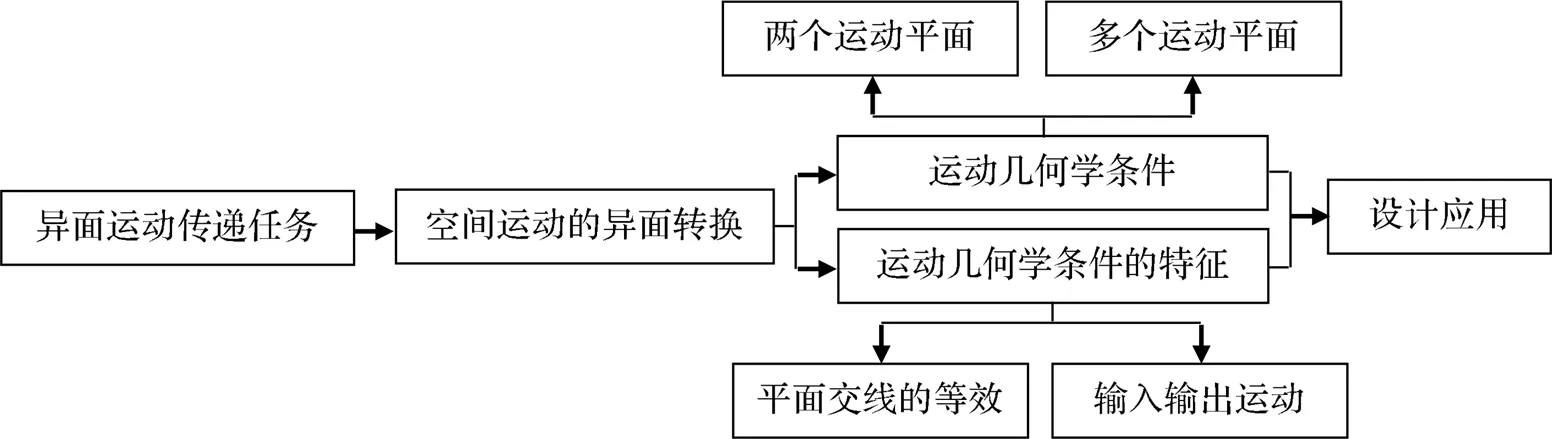
图1 整体研究内容
从运动传递的角度看,利用平面机构或简单平面构件组的组合来实现异面运动的转换,实质上是要求把平面π上的输入运动转换为平面π上的输出运动,且在整个运动传递过程中,输入构件和输出构件均分别保持在自己的运动平面上,所有其它活动构件也都在各自的运动平面上作相应的平面运动。因此,需研究运动在一系列平面中的传递。本章首先针对两平面间的运动联接进行讨论与分析,进而扩展到多平面的运动联接中,得出更具有普适性的结论。
1.1 两个不同运动平面的运动联接
在两运动平面的运动联接中,输入运动构件为输入运动平面π上的平面运动构件,其上任何一点的运动均在输入平面上。输出运动构件为输出运动平面π上的平面运动构件,其上任何一点的运动均在输出平面上。为了联接这两个异面的输入输出运动,首先要找到输入输出运动联接的运动几何学条件,并研究这一条件的几何特征。如果存在一个运动点,在运动过程中既在π上,又在π上,也就是说在π和π的公共部分运动,那么该点可视为同时在两个运动平面内运动,可分别在输入输出两个平面内通过中间平面构件组将输入构件和输出构件与该点联接起来。因此,异面运动联接的运动几何学充要条件为:在输入运动平面和输出运动平面之间的公共运动部分,至少存在一个运动的公共点。
对于不重合的两运动平面π和π,它们在空间的位置关系为平行或相交。当空间位置关系不同时,对应的运动几何学条件的特征不同,因此对它们分别进行讨论。
1.1.1 输入输出运动平面平行
平面运动的特征为在某一个平面运动或者与这个平面平行的平面内运动,均可认为是同一个平面运动。若输入运动平面π与输出运动平面π平行,则输入输出的相对运动可认为是同一个平面运动,作为两平面的运动公共点即联接点,可以取为π或π上的任意一点。此时可直接通过该点所在的平面运动构件将输入输出两平面的运动联接起来。
1.1.2 输入输出运动平面相交
若输入运动平面π与输出运动平面π相交,则输入输出的相对运动属于空间运动,且π上运动构件的运动与π上运动构件的运动为异面运动。此时,两平面的公共运动部分即为交线-。实现异面传动,就要找到其上存在运动公共点,满足上述充要条件。由于它的运动几何学条件的特征与交线处的异面转换运动形式紧密关联,因此,对位于π上的在交线处的传入运动形式和位于π上的从交线处的传出运动形式进行分析是有必要的。
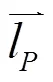
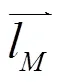
表1 交线处传入传出运动的组合形式

运动组合形式 圆周运动直线移动 圆周运动q-qq-l 直线移动l-ql-l

