多边形激励下动车组动态响应研究
张国平,张志波,吴兴文,蔡吴斌*,
多边形激励下动车组动态响应研究
张国平1,张志波1,吴兴文2,蔡吴斌*,2
(1.中车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
首先基于刚柔耦合理论,考虑了轮对、轴箱和构架的柔性,建立了动车组车辆刚柔耦合动力学模型;然后又通过模态叠加法建立了轨道的动力学模型,从而发展成车线-刚柔耦合动力学模型。随后,在车轮上施加20阶理想多边形,研究了300 km/h下轴箱垂向加速度、轮轨垂向力和轮轴弯曲应力的响应,结果表明:轴箱垂向加速度和轮轨垂向力以577 Hz的多边形通过频率波动,而轮轴弯曲应力主频为28.8 Hz的车轮转频,在此基础上,叠加了多边形的通过频率,因此多边形的通过频率577 Hz会分岔为548 Hz和605 Hz两个频率。通过对不同速度和不同多边形幅值下车辆响应的研究可以得到以下结论:随着速度和多边形幅值的增大,轮轨力最大值总体上呈现增大趋势。从轮轨力最小值上看:速度越大,多边形幅值越大,则更容易发生轮轨分离。当车轮多边形通过频率与轮轨耦合共振频率耦合,会引起轮轨垂向力的增大。当与轴箱自身模态频率耦合时会导致轴箱加速度的变大。轮轴应力则主要受到轮轨耦合共振模态以及轮轴自身的弯曲模态影响。
刚柔耦合动力学;车线耦合动力学;车轮多边形;轮轨垂向力;轮轴弯曲应力
近年来,我国高速铁路快速发展,但也遇到了一些轮轨磨耗问题。其中,车轮非圆化现象[1-2],即车轮多边形问题出现在部分高速动车组中。车轮多边形会引起轮轨高频异常振动,恶化簧下部件振动水平,进而可能会影响列车的运行安全。
关于车轮多边形的成因尚无定论。在瑞典,测试表明新车轮存在三阶多边形,经过分析[3],是在车轮的制造过程中,三角爪的车轮固定方式所导致。我国的地铁车辆中发现了9阶车轮不圆,李伟[4]对车辆进行了线路振动测量以及轮对模态测试,试验结果表明9阶车轮多边形是由轮对的一阶弯曲模态引起的。Morys[5]认为轮对的动不平衡会加速车轮的非圆化磨耗发展。通过建立动力学模型和轮轨磨耗模型,Johansson[6]再现了车轮多边形的发展,认为轨道的反共振以及轮轨耦合共振均有可能导致车轮多边形的产生。近年来我国高速铁路出现了高阶车轮多边形现象,对于250 km/h速度级的列车,车轮多边形以22~24阶为主;而对于300 km/h速度级的列车,多边形通常为17~20阶。Wu[7]通过试验研究表明,我国高速铁路的多边形符合“频率固定”机理,车轮多边形的阶数依赖于动车组的速度。Wu[8]和Cai[9]通过仿真再现了我国高速列车的高阶多边形生长过程,并认为其与钢轨的局部弯曲模态有关。
车轮多边形现象会引起轮轨力的异常波动,从而对车辆动力学性能、结构振动及轮轨噪声等均带来负面影响。张雪珊[8]通过车轮多边形对车辆稳定性的研究发现,车轮椭圆化可能导致车辆临界速度的下降,进而引起乘坐平稳性的恶化。王兴宇[11]研究了车内噪声与车轮多边形之间的关系,研究表明车内振动噪声的频率与车轮多边形磨耗的通过频率有对应关系,这意味着车轮多边形可以显著影响车内噪声。刘欢[12]分析了机车车轮多边形对其振动特性的影响,结果表明,通过车轮镟修可以显著降低机车振动水平。吴磊[13]研究了车轮多边形磨耗下的脱轨系数,虽然不同工况下的脱轨系数仍在安全限制之内,但需要指出的是:除了脱轨系数,车轮多边形还会引起车辆和轨道振动的加剧,进一步导致结构应力的增大,从而可能引发结构失效缩短结构寿命,带来安全性问题。Wu[14]针对多边形下激励的轮对疲劳损伤极限进行了研究,研究表明为了防止轮轴出现疲劳损伤,应缩短探伤的间隔。
基于此,本文针对车轮多边形,从振动、轮轨力和轮轴应力三个方面,系统地研究了车轮多边形对动车组动态响应的影响。通过仿真的手段,首先建立了动力学模型,包括刚柔耦合模型和车线耦合模型。其次,将理想的20阶多边形施加在车轮表面,对车辆的轴箱垂向加速度、轮轨垂向力和轮轴动态应力进行分析,研究其响应规律。最后,在不同的车速和不同的车轮多边形幅值下,分析了轴箱垂向加速度、轮轨垂向力和轮轴动态应力的变化规律。
1 车线刚柔耦合动力学模型
为研究车轮多边形下高速动车组动态响应,首先需建立动车组车线刚柔耦合动力学模型。
1.1 刚柔耦合动力学
由于车轮多边形的激励频率通常较高,传统的多刚体动力学模型覆盖的频率有限,难以满足车轮多边形的仿真要求,因此本文基于模态综合法和应力模态恢复法,考虑了构架、轮对和轴箱的柔性振动,建立了刚柔耦合动力学模型,如图1所示。
刚柔耦合动力学模型采用Simpack建立,并利用了其与有限元软件ANSYS之间的接口,基于子结构模态缩减技术,将各部件的模态信息导入到Simpack中[14]。其中,轮对考虑了固有频率1000 Hz以下的模态,图2是轮对的典型模态振型及其对应的固有频率。轮轴1阶至4阶的弯曲模态频率分别为113 Hz、191 Hz、363 Hz以及659 Hz,而在303 Hz和445 Hz时,轮对的模态振型则分别为轮盘的反相位和同相位伞状变形。在仿真中,本文不仅计算了轮对的柔性振动响应,同时也采用模态应力恢复技术,实时计算其动态应力。
此外,转臂式轴箱的固有频率相对较高,前两阶固有模态频率分别为535 Hz和579 Hz,从图3中可以看出,它们分别对应了转臂的一阶弯曲和扭转振型。
对于构架来说,总体频率相对较低,对高阶多边形激励下的响应影响较小。因此构架的模态在这里没有一一列出。
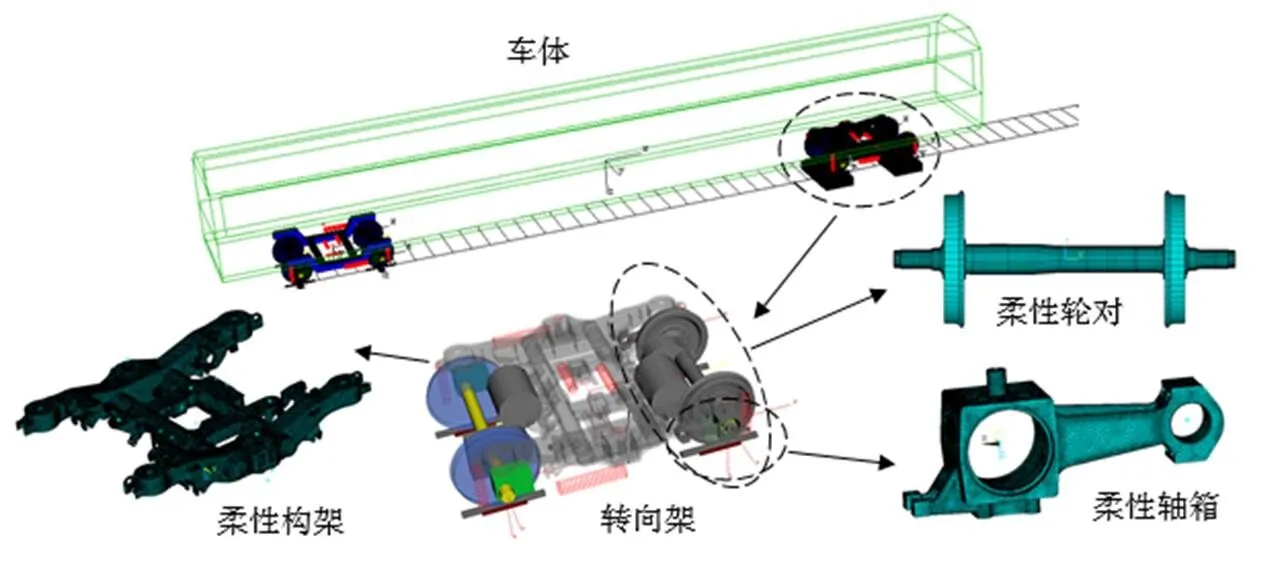
图1 动车组刚柔耦合动力学模型
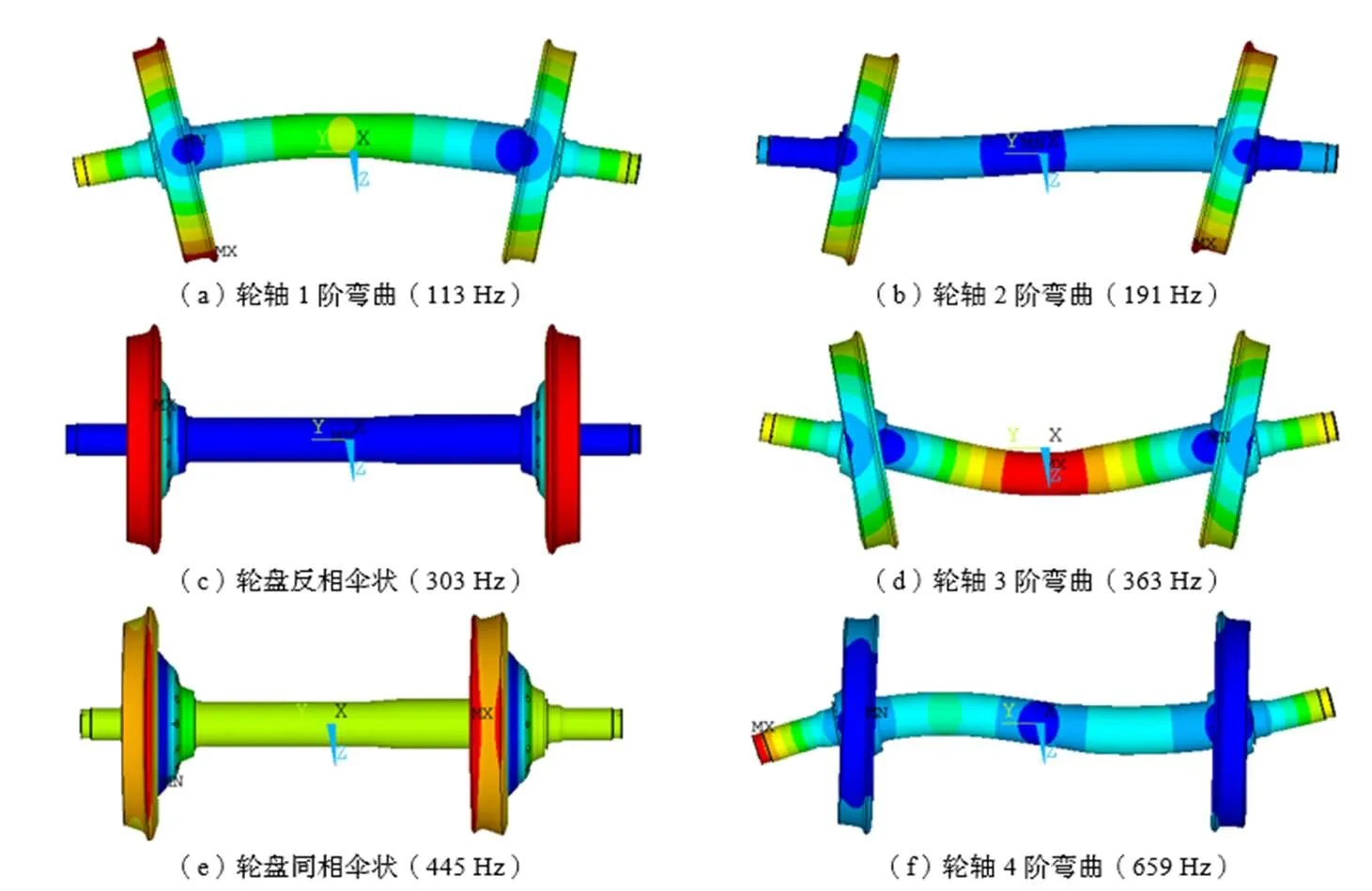
图2 轮对的模态振型
1.2 车线耦合动力学
除了车辆模型外,在轮轨界面高频的车轮多边形激振下,轨道的弹性变得不可忽视。因此本文在刚柔耦合模型的基础上,还基于车辆/轨道耦合动力学理论,建立了车线刚柔耦合动力学模型。在轨道模型中,本文针对CRTSI型板式无砟轨道,将钢轨考虑为离散支撑的铁木辛柯梁模型,轨道板则采用有限元的方法建模。它们的响应利用模态叠加法进行计算。扣件和轨道板下的弹性水泥砂浆层则用线性弹簧-阻尼单元来模拟。
基于铁木辛柯梁理论,钢轨的弯曲振动可由平动和界面转动两个偏微分方程表示,钢轨垂向振动如式(1)、式(2),横向振动如式(3)、式(4),扭转振动如式(5)所示。

图3 轴箱的模态振型

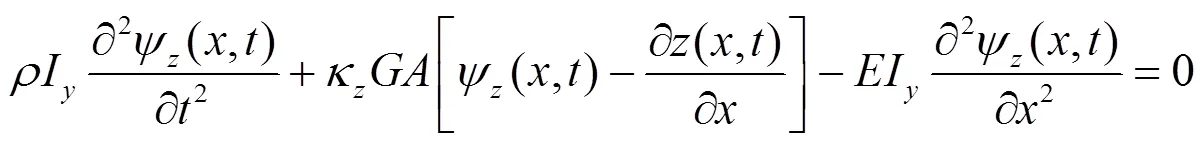
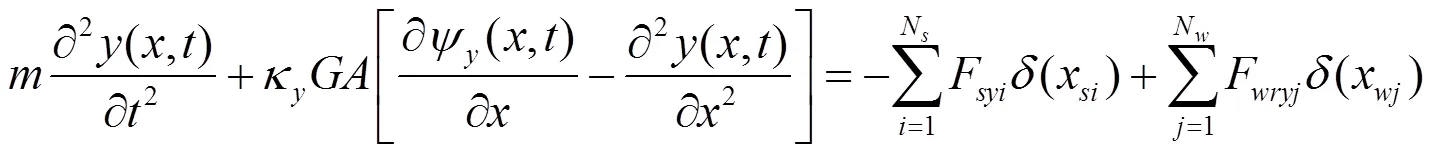
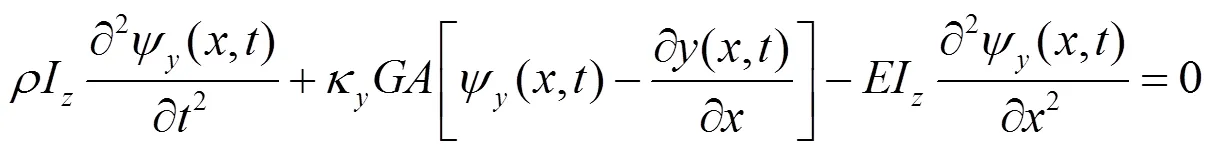
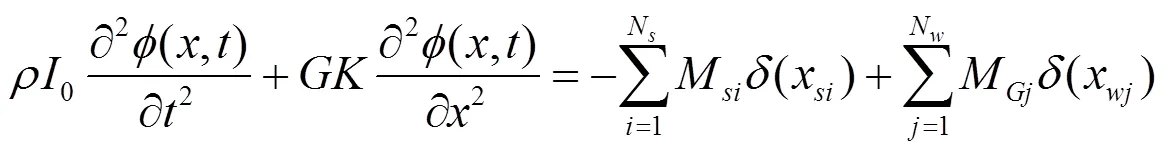
式中:为钢轨的纵向位置,m;为时间,s;为钢轨横向位移,m;为钢轨垂向位移,m;为钢轨扭转角度,rad;ψ为钢轨绕轴的截面转角,rad;ψ为钢轨绕轴的截面转角,rad;F为轨道第个支点垂向支承反力,N;F为轨道第个支点横向支承反力,N;F为第位车轮的轮轨垂向载荷,N;F为第位车轮的轮轨横向载荷,N;M为第支点处轨道支反力矩,N·m;M为第为车轮作用于轨道的力矩,N·m;为钢轨的弹性模量,Pa;I为钢轨截面对轴的惯性矩,m4;I为钢轨截面对轴的惯性矩,m4;0为钢轨的极惯性矩,m4;为钢轨单位长度密度,kg/m3;为钢轨剪切模量,Pa;为钢轨截面面积,2;κ为钢轨截面的垂向剪切形状因子;κ为钢轨截面的横向剪切形状因子;为狄拉克函数。
为了考虑板式无砟轨道的振动,在车辆轨道耦合动力学模型中将轨道板考虑成柔性体,用有限元实体单元建模,并利用模态叠加法进行求解。根据有限元理论其运动方程可描述为:
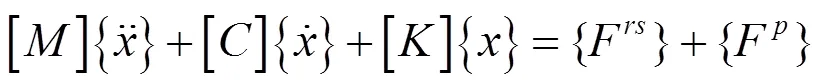
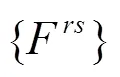
利用模态叠加法和轨道板的正则振型函数,轨道板全局坐标的运动方程可以转换成一系列解耦的方程,为:
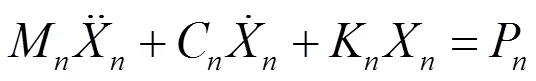
式中:X为轨道板正则坐标;M、C、K为轨道板广义正则质量矩阵、广义阻尼矩阵和广义刚度矩阵;P为广义正则载荷矩阵;为正则模态阶数。
1.3 多边形激励模型
本文仅考虑理想的车轮多边形激励,如图4所示。激励则可以表示为:
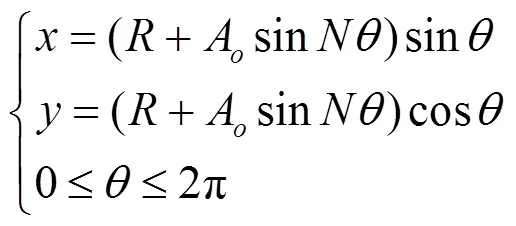
式中:R为车轮名义滚动圆处的半径,m;Ao为多边形的幅值;N为多边形阶数;为车轮旋转的角度,rad。
2 典型多边形激励下的响应
基于上文中建立的车线刚柔耦合动力学模型,本小节计算了典型的车轮多边形下动车组的响应,包括轴箱垂向加速度、轮轨垂向力和轮轴弯曲应力。在幅值为0.02 mm的20阶理想多边形激振下,300 km/h运行的动车组的响应(轮径920 mm)如图5所示。不难看出,轴箱垂向加速度和轮轨垂向力呈现谐波振动。其中,轴箱垂向加速度的幅值达到40,而轮轨垂向力的最大值接近100 kN,它们的振动频率为577 Hz,对应的车轮多边形的通过频率为:
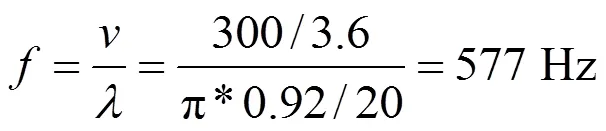
式中:v为车速,m/s;λ为多边形的波长,m。
轮轴的弯曲动应力响应与它们有所差异。图6是本文选取的轮轴弯曲应力测点,分别选取了左右轮盘的两侧,以及轮轴中点处的5个测点,在动力学计算时,实时输出它们的弯曲应力。从图5可见,轮轴的应力不仅存在577 Hz的高频振动,同时还呈现出以0.0347 s为周期的低频波动,通过计算发现,车轮转动一周需要的时间为:
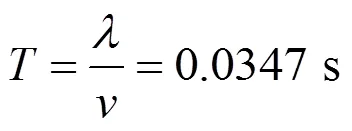
图7给出了无多边形工况和20阶多边形工况下的点C处的应力对比,可见,即使在没有多边形激励的情况下,车辆稳态运行时,在车体和构架的静载荷作用下,再加上轮对的旋转,轮轴上的节点必然会处于压缩-拉伸交替循环的状态,且其频率应该等于车轮的转频。在应力上则体现为在0上下波动,大于0表示拉伸,小于0表示压缩。当施加了20阶多边形后,在无多边形的基础上,又叠加了一个车轮多边形通过频率的波动。

图7 有无多边形激励下轮轴弯曲应力对比
图8对比了在20阶多边形激励下,车辆的轴箱垂向加速度、轮轨垂向力以及轮轴弯曲应力的频域特点:前两者以577 Hz的多边形通过频率为主频;弯曲应力主频为28.8 Hz的车轮转频,同时由于车轮转频的调制作用,车轮多边形的通过频率577 Hz会分岔为548 Hz和605 Hz两个频率。
3 车速和多边形幅值的影响
针对20阶车轮多边形,本节分析了不同车速和不同车轮多边形幅值对车辆响应的影响。图9为当车轮多边形幅值为0.02 mm时,车速对轮轨垂向力最大值和最小值的影响,从图中可见,总体上随着车速的升高,最大值呈现增长趋势,最小值呈现减小趋势。当车速为50km/h时,轮轨垂向力的幅值相对较大,这可能是因为此时车轮多边形通过频率(96 Hz)接近轮轨耦合共振频率。此外,当车速超过225 km/h后,轮轨垂向力最小值为0,这说明出现了轮轨分离现象。当车速超过250 km/h后,轮轨垂向力最大值大于170 kN,超过了我国《高速动车组整车试验规范》中对轮轨垂向力的限值要求。

图8 20阶多边形激励下车辆响应频域图

图9 不同车速下轮轨垂向力最大最小值(20阶,0.02 mm)
图10为200 km/h下,不同车轮多边形幅值下的轮轨垂向力最大值和最小值。从图中可见,在发生轮轨分离前(车轮多边形幅值小于0.14 mm),轮轨垂向力的最大值随着车轮多边形幅值的增长基本呈现线性增长的趋势,而最小值则呈现线性减小的趋势。当车轮多边形幅值大于0.14 mm后,出现了轮轨分离现象。
为进一步研究车轮多边形幅值和车速的影响,图11分析了当车速从50 km/h增加到400 km/h及车轮多边形幅值从0.02 mm增加到0.2
mm时,轮轨垂向力的响应。不难看出,其总体趋势与图10类似,从最大值上看:随着速度和车轮多边形幅值的增大,轮轨垂向力最大值总体上增大。从最小值上看:速度越大,车轮多边形幅值越大,则更容易发生轮轨分离现象。50 km/h处,轮轨垂向力的最大值出现峰值,最小值出现谷值,可能和轮轨耦合共振频率有关。
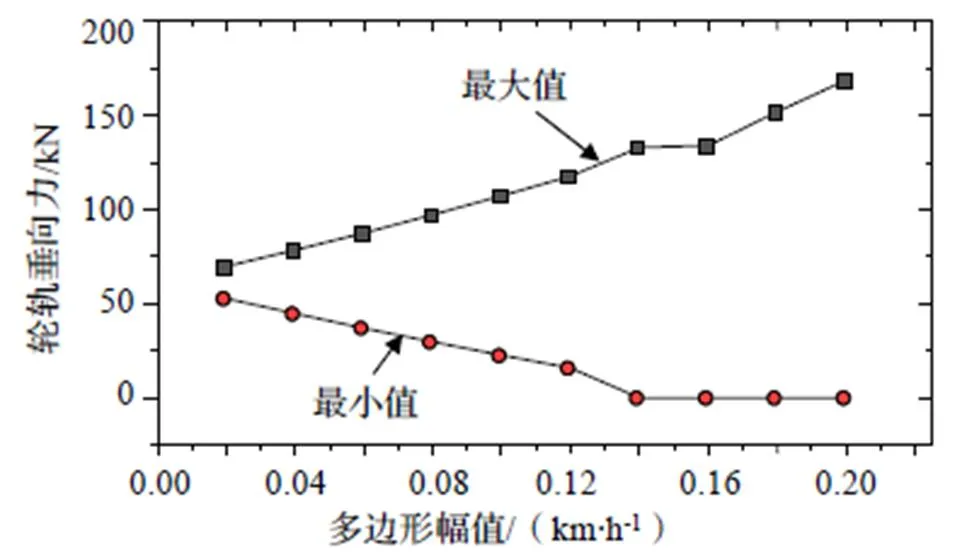
图10 不同幅值下轮轨垂向力最大最小值(20阶,200 km/h)

图11 不同车速和多边形幅值下轮轨力的最大最小值
图12为不同车轮多边形幅值和车速下轴箱垂向加速度的响应。可以看到:首先,随着车轮多边形幅值的增加,轴箱垂向加速度逐渐增加。其次,车速在300 km/h时,轴箱垂向加速度出现了峰值。且这个峰值并没有在轮轨垂向力中体现,所以这可能是由于轴箱自身的模态引起的。从上文可知,轴箱的转臂弯曲和扭转固有模态分别为535 Hz和575 Hz;而300 km/h时20阶多边形的通过频率为577 Hz,与它们接近。从而导致轴箱自身的共振,进一步引起了轴箱垂向加速度的增大。
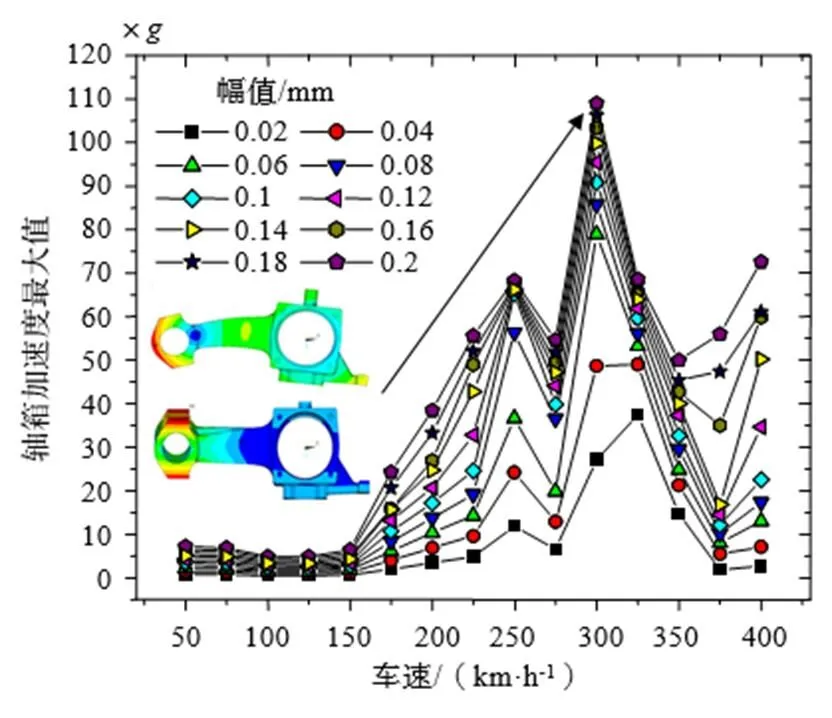
图12 不同车速和多边形幅值下的轴箱加速度最大值
图13为车轮多边形幅值和车速对轮轴弯曲应力的影响。本文选取了轮轴中心的点进行研究。随着多边形幅值的增加,轮轴的弯曲应力是增加的。但车速并不是单调的趋势,在车速50 km/h和250 km/h时,点处的弯曲应力出现了峰值。前者如前文所述,可能是由轮轨耦合共振所引起。
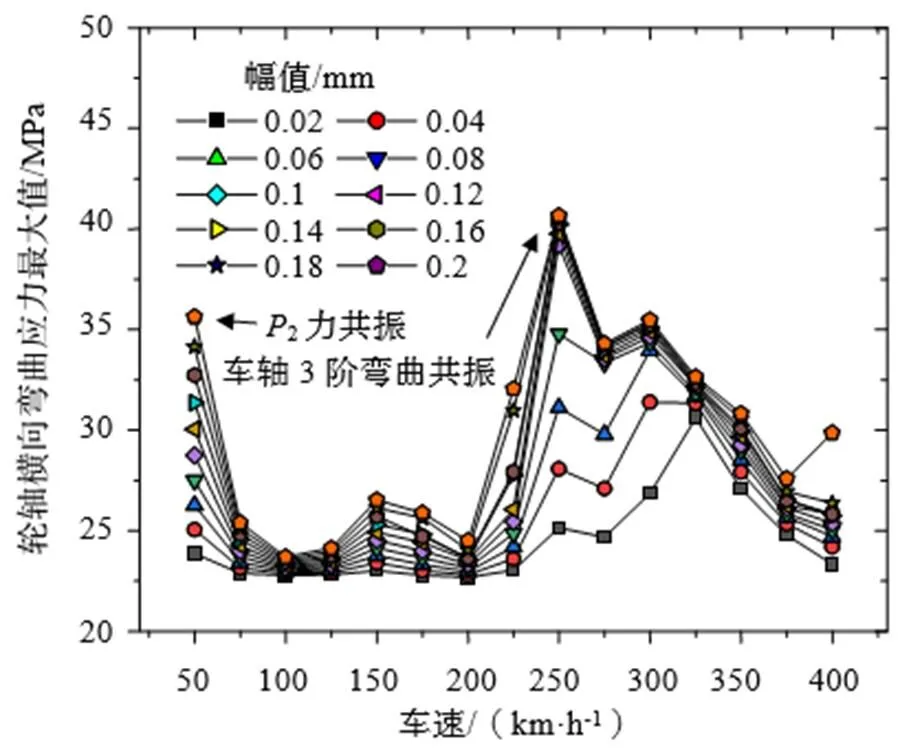
图13 不同车速和多边形幅值下的轮轴弯曲应力最大值
对于250 km/h处的峰值,其对应的通过频率为481 Hz,这可能与车轴的3阶弯曲共振有关,从上文可知,虽然车轴的3阶弯曲模态在自由状态下仅有363 Hz,但在一系和轮轨的约束下,在约束状态下其模态频率为504 Hz,与车轮多边形的通过频率接近,从而引起共振,使得弯曲应力显著增大。
4 结语
本文考虑了轮对、轴箱和构架的柔性振动,以及轨道的弹性,建立了车线-刚柔耦合动力学模型。对20阶多边形激励下车辆的响应,包括轴箱垂向加速度、轮轨垂向力和轮轴弯曲应力进行研究,可以得到以下结论:
(1)在20阶多边形激励下,轴箱垂向加速度和轮轨垂向力的波动以577 Hz的车轮多边形通过频率为主频;而轮轴弯曲应力主频为28.8 Hz的车轮转频,同时由于车轮转频的调制作用,车轮多边形的通过频率577 Hz会分岔为548 Hz和605 Hz两个频率。
(2)随着速度和车轮多边形幅值的增大,轮轨垂向力最大值总体呈现增大趋势。从轮轨垂向力最小值上看:速度越大,车轮多边形幅值越大,则更容易发生轮轨分离现象。
(3)50 km/h时,轮轨垂向力最大值出现峰值、最小值出现谷值,可能和轮轨耦合共振频率有关。300 km/h时,轴箱垂向加速度出现峰值,是因为车轮多边形的通过频率577 Hz与轴箱的转臂弯曲和扭转固有频率535 Hz和575 Hz相接近,引发轴箱自身共振引起。
(4)轮轴的弯曲应力关于车速不是单调的,轮轨耦合共振以及轮轴的弯曲模态共振均可能导致轮轴弯曲应力的增大。
[1]Nielsen J C O,Johansson A. Out-of-round railway wheels-a literature survey[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit,2000,214(2):79-91.
[2]Johansson A,Nielsen J O. Out-of-round railway wheels-wheel-rail contact forces and track response derived from field tests and numerical simulations[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit,2003,217(2):135-146.
[3]PALLGEN G. Unrunde rader an eisenbahnfahraeugen[J]. Der Eisenbahningenieur,1998,49(1):56-60.
[4]李伟,李言义,张雄飞,等. 地铁车辆车轮多边形的机理分析[J]. 机械工程学报,2013,49(18):17-22.
[5]MORYS B,KUNTZE H B.,Hirsch, U.. Investigation of origin and enlargement of out-of-round phenomena in high speed ICE-wheelsets[C]. In Proceedings of 10th European ADAMS Users’ Conference,Frankfurt: s.n.,1995:14.
[6]Johansson A,Andersson C. Out-of-round railway wheels—a study of wheel polygonalization through simulation of three-dimensional wheel–rail interaction and wear[J]. Vehicle System Dynamics,2005,43(8):539-559.
[7]Yue W U,Xing D U,Zhang H J,et al. Experimental analysis of the mechanism of high-order, polygonal wear of wheels of a high-speed train[J]. 浙江大学学报:A卷英文版,2017(18):592.
[8]X. Wu,S. Rakheja,W. Cai,M. Chi,A.K.W. Ahmed,S. Qu. A study of formation of high order wheel polygonalization[J]. Wear,2019(424-425):1-14.
[9]W. Cai,M. Chi,X. Wu,F. Li,Z. Wen,S. Liang,X. Jin. Experimental and numerical analysis of the polygonal wear of high-speed trains[J]. Wear,2019:203079.
[10]张雪珊,肖新标,金学松. 高速车轮椭圆化问题及其对车辆横向稳定性的影响[J]. 机械工程学报,2008,44(3):50-56.
[11]王兴宇,范军. 高速列车车内噪声与车轮不圆顺关系的研究[J]. 铁道学报,2013(9):18-22.
[12]刘欢,陶功权,罗贇,等. 机车异常振动原因分析和控制措施研究[J]. 机械,2019(8):1-7.
[13]吴磊,钟硕乔,金学松,等. 车轮多边形化对车辆运行安全性能的影响[J]. 交通运输工程学报,2011(3):51-58.
[14]X. Wu,M. Chi,H. Gao. Damage tolerances of a railway axle in the presence of wheel polygonalizations[J]. Engineering Failure Analysis,2016(66):44-59.
[15]包学海. 高速客车车体和构架结构振动研究[D]. 成都:西南交通大学,2009.
Dynamic Response of EMUs in the Presence of Wheel Polygonal Excitations
ZHANG Guoping1,ZHANG Zhibo1,WU Xingwen2,CAI Wubin2
( 1.CRRC Qingdao Sifang Co., Ltd., Qingdao 266111, China; 2.State Key Laboratory of Traction Power, Soutwest Jiaotong University, Chengdu 610031, China )
Based on rigid-flexible coupling theory, rigid-flexible dynamic model of high speed vehicle is established, taking flexibility of wheelset, axle box and bogie frame into consideration. Using the modal superposition method, dynamic model of track is also established. The traditional vehicle dynamic model is improved to vehicle-track and rigid-flexible coupling model. Through applying the 20thorder ideal polygon on the wheel, the response of the axle box vertical acceleration, wheel/rail vertical force and bending stress of the wheelset axle are investigated at the speed of 300 km/h. The results suggest that the axle box vertical accelerations and wheel/rail vertical forces fluctuate at the frequency of 577 Hz, namely, the passing frequency of the polygon. While the dominating frequency of the wheelset axle bending stress is 28.8Hz, which accords with the rotation frequency of the wheel, the passing frequency of the polygon is separated into two peaks at 548 Hz and 605 Hz. Moreover, the effect of vehicle speed and amplitude of the polygon on the dynamic response of the vehicle are studied. The results show that the overall trend of the maximum value of wheel/rail vertical forces increases with the rising of speed and polygon amplitude. As for the minimum value of the forces, the higher speed and larger amplitude would easily lead to the wheel/rail separation. The wheel/rail vertical forces would increase when the passing frequency of polygon is closed to the frequency coupled wheel/track resonance mode. Furthermore, the resonance of the axle box increases axle box acceleration. The wheelset axle stress is mainly influenced by the coupled wheel/track resonance mode and wheelset bending modes.
rigid-flexible dynamic model;coupled vehicle-track dynamic model;wheel polygonal wear;wheel/rail vertical forces;wheelset axle stress
U270.1
A
10.3969/j.issn.1006-0316.2020.05.011
1006-0316 (2020) 05-0067-08
2019-12-05
张国平(1986-),四川南充人,工程师,主要研究方向为机车车辆转向架设计。*通讯作者:蔡吴斌(1991-),男,江苏无锡人,博士研究生,主要研究方向为铁道车辆系统动力学,Email:wubin0410@hotmail.com。

