基于离散蒙特卡洛的一种3T1R并联机构工作空间分析

李旭，罗霞，罗成，孙淼

基于离散蒙特卡洛的一种3T1R并联机构工作空间分析

李旭1，罗霞1，罗成1，孙淼*,2

（1.东方电气集团东方汽轮机有限公司，四川 德阳 618000；2.四川省机械研究设计院，四川 成都 610063）

针对一种拓扑结构为2-PRPU型的3T1R空间并联机构，采用离散式蒙特卡洛法，通过对动平台转动自由度作离散化处理，在输入对称的情况下，实现了整个空间并联机构的定姿态工作空间、可达工作空间和灵活工作空间的可视化。从定姿态工作空间、灵活工作空间和可达工作空间的角度分析2-PRPU型空间并联机构的工作性能，表明该机构动平台的可达工作空间范围较大，且大部分为灵巧工作空间。这为多自由度空间并联机构的研究和应用提供理论基础。

3T1R；并联机构；工作空间；离散蒙特卡洛

并联机构是具有两个或两个以上自由度，且以并联方式驱动的一种闭环机构[1-2]，其中3T1R并联机构[3-6]能够实现三个方向的平移和绕一个轴的转动。根据所绕轴线的不同，可将3T1R机构分为3T1R、3T1R、3T1R，即动平台可实现三维平动（,,）和分别绕、、轴的转动[7]。目前应用最多的是3T1R型并联机构。在实际生活中，3T1R并联机构由于刚性好、动态性能好等优点在快速抓取、高速分拣等领域被大量应用。工作空间是3T1R机构工作性能的重要指标之一，通过对工作空间的可视化研究可以帮助设计人员完善和改进机构设计，帮助控制人员完成路径规划等。

并联机构工作空间的研究方法主要有解析法、图论解法及数值法[8]，其中以解析法和数值法最为常见。解析法具有较高的精度，但依赖于求解机构运动学正解，而对并联机构而言，正解求解过程一般非常繁琐。数值法既可依赖于机构运动学正解也可依赖于机构运动学反解，由于正解求解困难，故数值法一般通过机构的运动学反解分析工作空间。文献[9-10]使用数值法分析了六自由度并联机构的工作空间。文献[11-12]采用极坐标搜索法研究3-RRR平面并联机器人的工作空间边界，并对边界进行了优化。文献[13]采用基于混沌映射算法的水波法对并联机构的工作空间进行快速搜索，并对相应的机构参数进行了优化研究。文献[14]中通过D-H方法建立3-PRRU并联机构的正解数学模型，得到非线性方程组，利用MATLAB数值求解方程，实现了工作空间的仿真。

1 2-PRPU机构描述与分析

本文研究的2-PRPU型3T1R空间并联机构如图1所示。O-yz和O-yz分别为固定在机架和动平台上的笛卡尔坐标系，它们通过2个PRPU支链相互连接，每个PRPU支链包含一个与机架相连的PR副（P副与R副组成一个C副），C副的轴线平行于U铰链中第一个R副的铰链。动平台通过2个R副与2个支链相连，两个R副的轴线相互平行并且在运动中一直保持平行关系。1和3分别是点1和2到定坐标系原点O的距离，表示两个与机架相连的P副的输入运动变量。2和4分别是构件11与22的长度（即支链长度），表示剩下两个P副的输入运动变量。表示构件12的长度。姿态角是构件12与轴间的夹角（逆时针方向为正），表示了动平台的转动运动。角度θ（＝1,2,…,6）分别表示了6个R副的副变量。1和θ2、4和5、3和6依次为与轴、、的逆时针方向夹角。

图1所示机构中，两个C副的轴线分别平行于轴和轴，因此两个U铰链的第二个R副的轴线均平行于轴。1和2是两个U铰链的几何中心。1（2）是1（2）到轴（）垂线的垂足。两个U铰链的第二个R副的轴线方向必须保持相互平行，而两个U铰链的第一个R副转动方向均由各自相连的PRPU支链从几何上确定。因此，在运动过程中动平台法方向不变，动平台始终绕（）轴旋转。

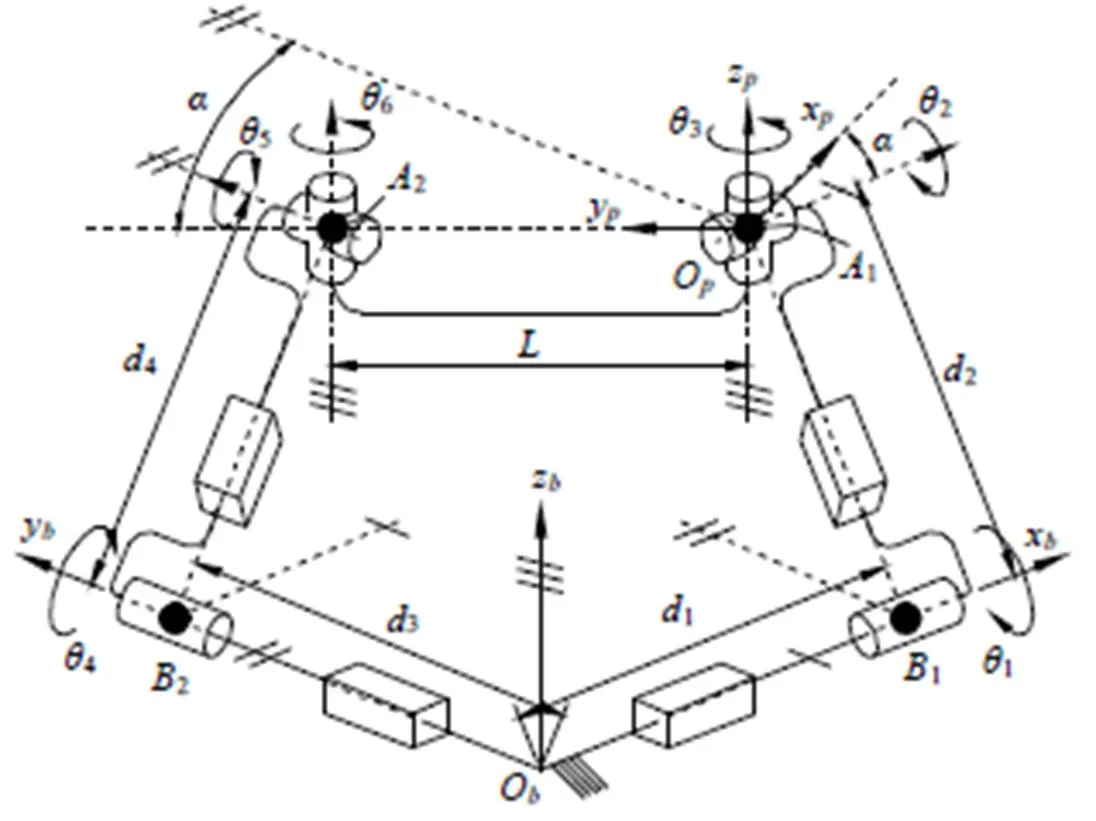
图1 机构示意图

2 机构的位置反解与约束条件

以四元组(1,2,3,4)T表示输入运动空间中的一点，1、2、3和4对应各个驱动器的运动变量。以在定坐标系O-yzb中动平台上点1坐标(1,1,1)和姿态角唯一表示动平台的位姿。以四元组(1,1,1,)T表示工作空间中的一个点，即机构的实际工作空间由(1,1,1,)T的集合表示。

直接由图1可以得下列关系：

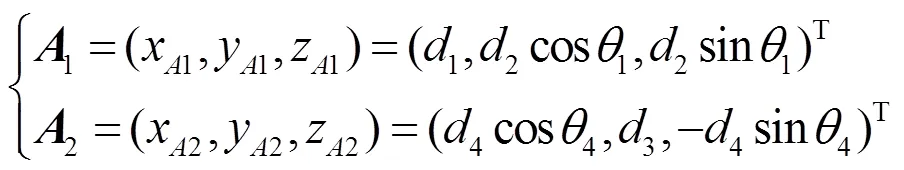
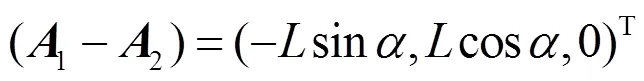
式中：1、2、1、2为在坐标系O-xyz中对应各点的坐标向量。

运动学反解分析是在给定动平台位姿的情况下，找到所有满足约束条件的驱动器参数，即在给定(1,1,1,)T的情况下，找到所有的(1,2,3,4)T。在本文研究的2-PRPU型3T1R并联机构中，一旦给定1、1、1和，输入运动参数1和2可以计算为：

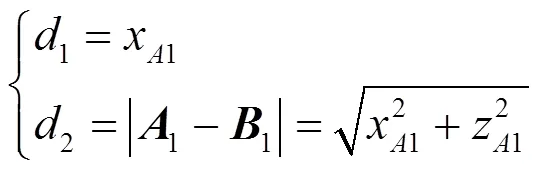
然后，2点的坐标可以由式（3）算出：

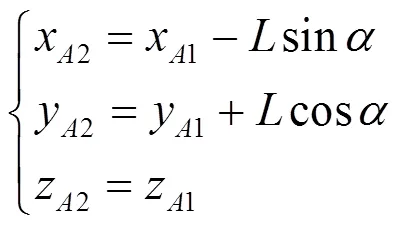
最后，剩下的输入运动参数3和4计算为：

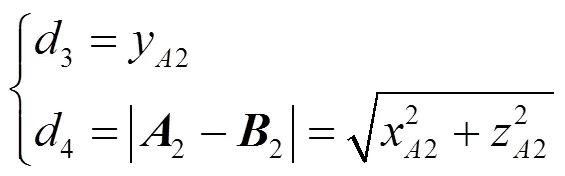
考虑对应于实际情况的P副一般由直线电机或者油缸等驱动器驱动，其直线行程有一定范围，相应地假设该2-PRPU型3T1R并联机构中四个P副的直线输入运动在一定范围内且均为[0,20]。则可有如下工作空间约束条件：

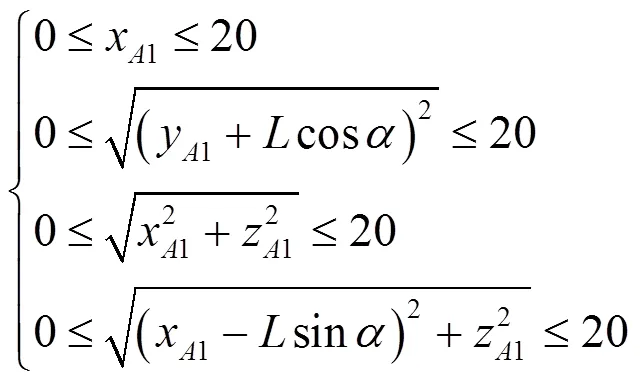
3 并联机构工作空间分析的离散式蒙特卡洛法原理

3T1R机构包含四个自由度，其可视化相对较难，往往需对其降维。本文采用的离散式蒙特卡洛法不但可应用于最常见的3T1R型四自由度并联机构，亦可用于3T1R型和3T1R型。

离散式蒙特卡洛法基于蒙特卡洛法，是一种利用“随机数”或“伪随机数”结合机构运动学反解进行并联机构工作空间可视化分析的方法，其适用于绝大多数3T1R空间并联机构。关于离散式蒙特卡洛法的具体原理介绍及算法流程可以参考文献[15]。结合前期的工作，可以给出应用Mathematica软件分析该2-PRPU并联机构的算法，如图2所示。

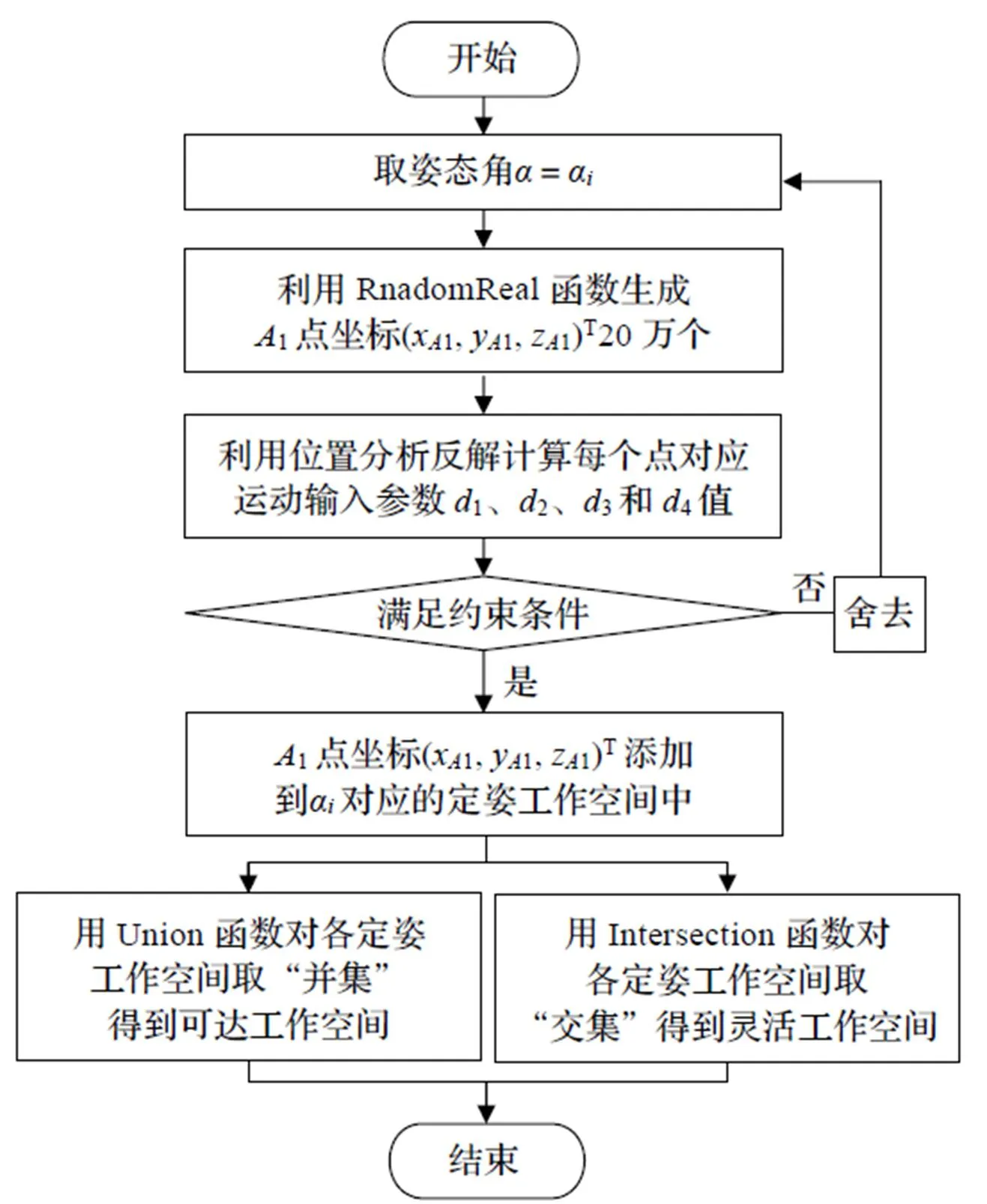
图2 计算流程图

4 工作空间可视化分析

下面以本文中的2-PRPU型3T1R空间并联机构工作空间可视化为例，在Mathematica中可视化分析机构的定姿态工作空间、灵活工作空间和可达工作空间，相关参数如表1所示。

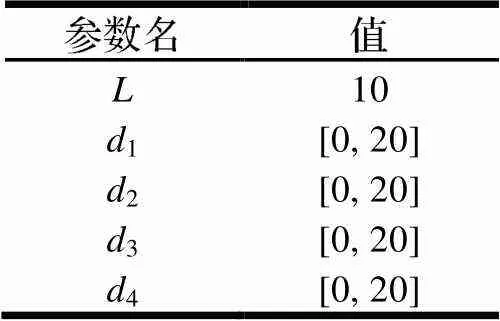
表1 机构相关参数表

4.1 定姿态工作空间

定姿态工作空间是指机构的动平台在约束条件下以某一固定姿态，动平台参考点能够到达的所有位置的点的集合[16]。本文机构中，用前面所述的角表示动平台的绕（）轴的姿态夹角，1为动平台参考点，则定姿态工作空间S是取定每一个α角对应的1点所能达到的范围。这里取姿态角为0、π/4、π/2、3π/4、π对应的定姿态工作空间如图3所示。

图3 姿态角为0、π/4、π/2、3π/4、π时定姿态工作空间

从图3可以看出，当姿态角为π时，工作空间是最大；当姿态角为π/2时，工作空间最小。姿态角从0～π过程中，工作空间呈现先逐渐较小后逐渐增大的趋势。

4.2 可达工作空间

机构的可达工作空间指在结构限制下机构动平台的姿态角在0～2π范围内连续变化，所得到的所有定姿态工作空间的并集[17]。从图4可以看出，该并联机构的可达工作空间体积较大，边界清晰且内部无空腔或空洞，机构动平台运动范围较大。这有利于该型3T1R并联机构的实际应用，也能为在该机构基础上改进大工作空间的并联机器人提供参考。

4.3 灵活工作空间

灵活工作空间指机构末端执行器任意能够到达的区域[18]。灵活工作空间范围越大说明机构的工作性能越好。给出2-PRPU型3T1R空间并联机构的灵活工作空间如图5所示，可以看出该机构的灵活工作空间占可达工作空间的比例较大，因此该机构具有较好的工作性能。

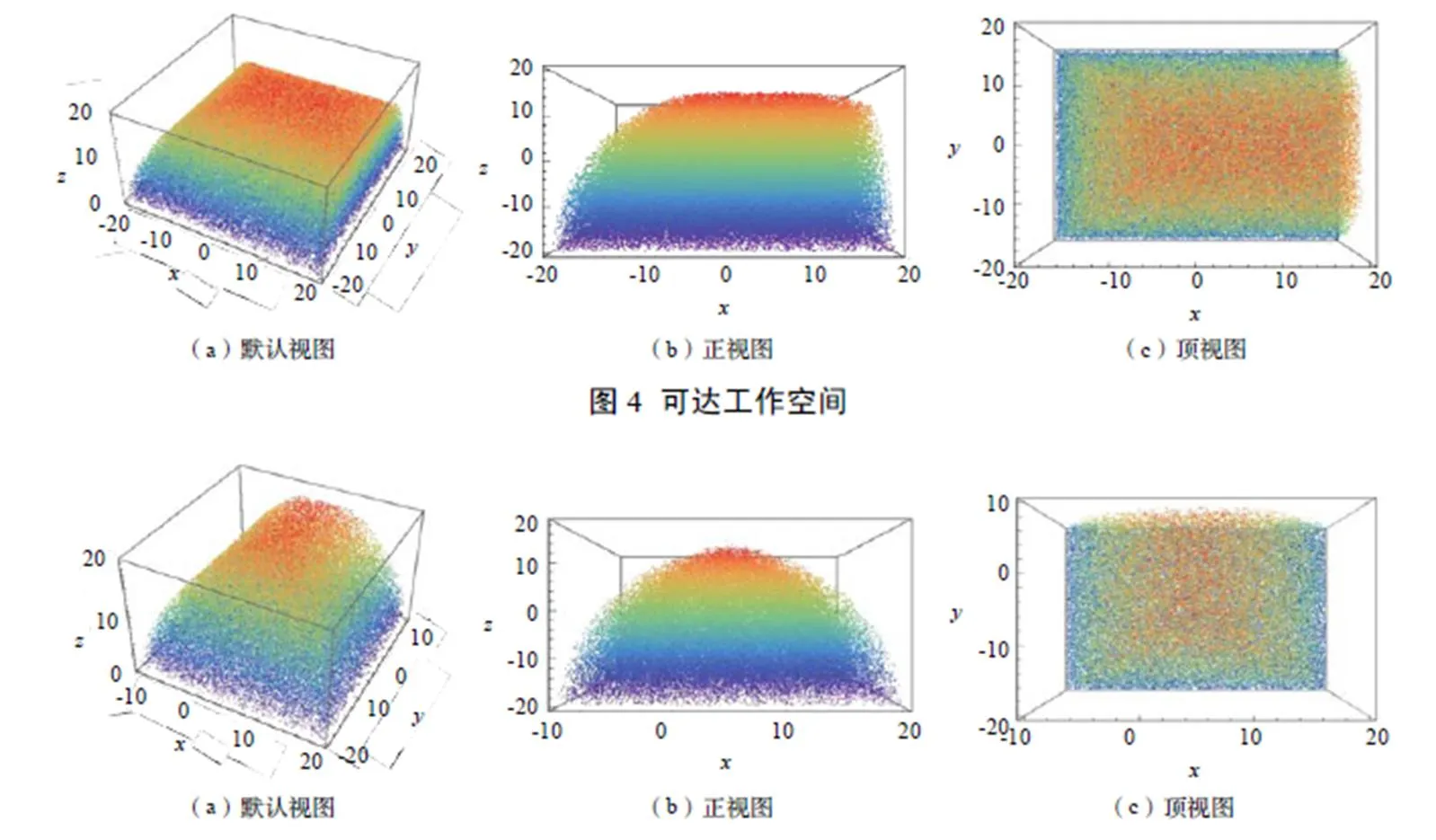
图5 灵活工作空间

5 结论

结合离散式蒙特卡洛法分析了2-PRPU型3T1R空间并联机构的定姿态工作空间、可达工作空间、灵活工作空间，结果表明该2-PRPU的定姿态工作空间随姿态角变换而变化，且在姿态角为π时最大。通过各姿态角对应的定姿态工作空间的并集，可得该机构的可达工作空间，从可达工作空间的可视化结果可看出，该机构的动平台能到达的空间范围较大，这将为该机构的实际应用奠定有利基础。通过各姿态角对应的定姿态工作空间的交集得到该机构的灵活工作空间，可发现灵活工作空间占可达工作空间的比例较大，但还有提升空间，这将为以后改进该机构提供参考。

[1]翟庆钟，王卫兵，冯静安，等. 基于Stewart平台的六轴并联机床的研究[J]. 机械，2013（11）：23-26.

[2]汪苏，怀其武，苗新刚，等. 一种二自由度并联机构设计及空间误差建模[J]. 机械，2012（8）：7-11.

[3]Amine S，Mokhiamar O，Caro S. CLASSIFICATION OF 3T1R PARALLEL MANIPULATORS BASED ON THEIR WRENCH GRAPH[J]. Journal of Mechanisms & Robotics，2017，9（1）：011003.

[4]石志新，叶梅燕，罗玉峰，等. 3T1R并联机构结构设计与位置分析[J]. 农业机械学报，2016，47（8）：364-369.

[5]涂叶凯. 3T1R并联机构运动学分析与尺度优化[D]. 杭州：浙江理工大学，2018.

[6] Tu Y.，Chen Q.，Ye W.，et al. Kinematics, singularity, and optimal design of a novel 3T1R parallel manipulator with full rotational capability[J]. Journal of Mechanical Science and Technology，2018，32(6)：2877-2887.

[7]朱伟，顾开荣，王传伟，等. 一种3T1R并联机构设计及运动学性能分析[J]. 中国机械工程，2018，29（1）：14-21.

[8]刘志忠，柳洪义，罗忠，等. 机器人工作空间求解的蒙特卡洛法改进[J]. 农业机械学报，2013，44（1）：230-235．

[9]Arai T，Cleary K，Nakamura T，Adachi H，Homma K. Design, analysis and construction of a prototype parallel link manipulator [C]. IEEE International Workshop on Intelligent Robots and Systems IROS’90，1990：205-212.

[10] Fichter E F. A Stewart-Platform based manipulator: general theory and practical construction[M]. Sage Publications Inc.，1986.

[11]曹丽亚，崔建昆，宋亚楠. 3-RRR平面并联机器人工作空间边界求解和灵活性研究[J]. 机械传动，2016，40（8）：38-42.

[12]朱心平，崔建昆，张源. 求解3-RRR平面并联机器人工作空间的迭代搜索法[J]. 机械研究与应用，2010（3）：48-49.

[13]夏永强，罗玉峰，石志新，等. 基于水波法的并联机构的工作空间分析与参数优化研究[J]. 机械传动，2018（6）：58-63.

[14]刘家念. 3-PRRU并联机器人的运动学分析[D]. 天津：天津理工大学，2013.

[15]陈光平，韩远飞，肖铁忠. 基于计算机的空间并联机构工作空间的可视化分析（英文）[J]. 机床与液压，2018，46（12）：139-144.

[16]Snyman J A，Plessis L J D，Duffy J. An Optimization Approach to the Determination of the Boundaries of Manipulator Workspaces[J]. Journal of Mechanical Design，2000，122（4）：447-456.

[17]夏永强，罗玉峰，石志新，等. 3T1R并联机构的工作空间与参数优化[J]. 机械设计与研究，2017（6）：10-14.

[18]朱海飞，管贻生，吴文强，等. 基于二分逼近原理的定姿态工作空间快速搜索方法[J]. 机器人，2013，35（6）：709-715.

A Discrete Monte Carlo Approach to Workspace Analysis of a Type of 3T1R Parallel Mechanism

LI Xu1，LUO Xia1，LUO Cheng1，SUN Miao2

(1.Dongfang Turbine Co., Ltd., Dongfang Electric Corporation, Deyang 618000, China; 2.Sichuan Provincial Machinery Research & Design Institute, Chengdu 610063, China)

The paper studies a type of 3T1R spatial parallel mechanism with the topology of 2-PRPU. Discrete Monte Carlo approach is applied to perform the discretization of the rotational degrees of freedom of the moving platform, which enables the visualization of the fixed-orientation, reachable and dexterous workspace of the mechanism with symmetrical inputs. The performance analysis of 2-PRPU mechanism based on fixed- orientation, reachable and dexterous workspace indicates that the reachable workspace of the mechanism’s moving platform is large and the dexterous workspace accounts for a large proportion of the reachable workspace, which laid the foundation of the research and application of multi-DOF parallel mechanism.

3T1R；parallel mechanism；workspace；discrete Monte Carlo

TH112

A

10.3969/j.issn.1006-0316.2020.05.005

1006－0316 (2020) 05－0027－06

2020－01－06

四川省科技计划（国际合作）资助项目（2018HH0144）

李旭（1977－），男，四川资阳人，高级工程师，主要研究方向为机械设计及制造。*通讯作者：孙淼（1987－），男，四川德阳人，工学硕士，工程师，主要研究方向为机构学、机电控制，E-mail：sunmiao198@sina.com。