基于改进局部二值模式算法的中草药图像鉴别
陶 佳,王 芳,沈红岩,高 媛
(河北农业大学 信息科学与技术学院,河北 保定 071000)
目前在世界范围内,中草药受到的关注度正在日益提升,我国的中草药行业正面临着巨大的发展机遇。中草药的质量关系着病症的疗效,所以对其进行科学地鉴别分类是十分必要的。传统的中草药分类及质量评估涉及到性状鉴别和显微鉴别,这2个方面均有赖于人的观察和经验,鉴别效率偏低,主观意识强,不能满足中医中药产业化发展的客观需求。因此对中草药进行准确、高效地鉴别就成为现今研究热点。一些研究借助信息技术和图像处理来实现对中草药的鉴别,文献[1-4]分别通过改进的傅里叶描述子、边缘梯度、小波变换、神经网络等方法对叶片、脉络等图像进行特征提取及分类检索,取得了一定的效果。但这些研究成果还难以满足中草药分类鉴别的全部需求,首先是针对中草药显微图像鉴别的成果依旧不多见,对显微图像的特征集筛选缺乏成熟的方案;其次是结合中草药图像固有的纹理特征和旋转不变性特征,缺乏1 种描述局部纹理的成熟模型将具有不同角度的纹理图像归为一类;三是未能对传统的分类算法进行优化,使之能够更加适用于中草药图像鉴别。笔者以中草药中的藤茎类为研究对象,取其横切显微图像的颜色特征及纹理特征,以颜色直方图来描述目标对象的颜色特征;分析局部二值模式算法在处理中草药显微图像时的优势及不足,引入邻域点灰度值间的关系对其进行优化改进,提取图像的纹理特征;引入K 近邻分类器进行训练,并改进了传统分类器导致出现多个最优点的不足,最终实现了更加准确的图像鉴别。本文研究结果可对图像处理和人工智能技术在中草药方面的应用起到一定的借鉴作用。
1 图像特征提取
笔者对藤茎类中草药横切显微图像进行识别。1幅显微图像在颜色方面往往较为单一,能够作为鉴别分类的标准之一。而显微图像更多的信息则包含在其纹理特征里,因此纹理特征可以作为图像鉴别分类的主要标准。藤茎类中草药的显微图像具有十分复杂的纹理,且这些纹理存在旋转性,必须采取旋转不变性纹理特征提取方法,才能保证将具有不同角度的纹理图像准确归类。
1.1 显微图像颜色特征提取
很多模型都能实现对图像的颜色特征进行描述和提取,包括RGB(红/绿/蓝)模型、HSV(色度/饱和度/亮度)模型、CMYK(青/红/黄/黑)模型等等。结合这些模型的优缺点及适用范围[5],本研究为对藤类横切面显微图像的颜色特征进行提取,最终选取基于HSV 的模型来实现。
图像的颜色直方图能够以直方图的形式,通过统计所有颜色分量在目标对象中的占比来描述其颜色特征。颜色直方图与目标的大小和方向均不相关,所以最终选取HSV 直方图对显微图像颜色特征进行提取。具体步骤为[6]:
(1)将格式为RGB 的目标图像转换为HSV 图像,从而更精确地描述像素颜色特征,方法为:

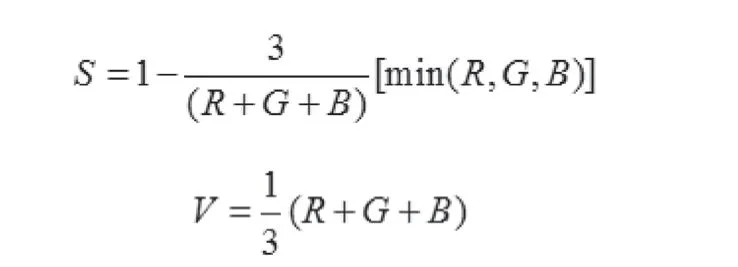
(2)对HSV 图像的分量进行量化处理。本研究将H、S、V 3 个空间进行划分,原因是结合人类视觉的生理特点,方法为:

(3)构建基于HSV 空间的一维颜色直方图,方法为:
G=9H+3S+V,G ∈[0, 71]。
这样便把H、S、V 三维空间转换成了一维矢量G。
1.2 横切显微图像纹理特征提取
横切显微图像的纹理特征往往十分复杂,且同种纹理图像经常旋转变化,这就要求纹理特征的提取和描述应该满足旋转不变性。传统的一些成熟的纹理特征描述方法包括基于结构的方法、基于模型的方法、基于统计的方法等等,但大部分方法均无法满足对于复杂纹理的旋转不变性描述。局部二值模式(Local Binary Pattern,LBP)是近年来受到广泛关注的1 种纹理提取及描述方法,其优势在于能够满足目标图像的灰度不变,同时符合旋转不变的需求。本研究选取基于局部二值模式的纹理特征提取方法。针对传统局部二值模式难以完好地体现邻域点间灰度变化的不足,引入邻域点间的关系对其进行优化,从而体现出目标图形更完整的微观纹理信息。
1.2.1 传统局部二值模式 基于局部二值模式的图像特征提取最初来自于T.Ojala[7],因为其时间复杂度低,可以提取出较多的纹理特征,因此逐渐被应用和推广。其原理如图1 所示。

图1 传统局部二值模式说法原理示意Fig.1 A schematic illustration of the local binary patterns
局部二值模式设置窗口对目标图像进行遍历。以3×3 窗口为例,对每1 个遍历经过的点,均把此点像素的灰度值与四周的像素点(共计8 个)的灰度值比较。如果灰度值高于此点则设置为1,如果灰度值低于此点则设置为0。
设像素点个数为P,局部二值模式的窗口半径是R,窗口中心坐标为(Xc,Yc)则局部二值模式算子LBP 可以表示为:
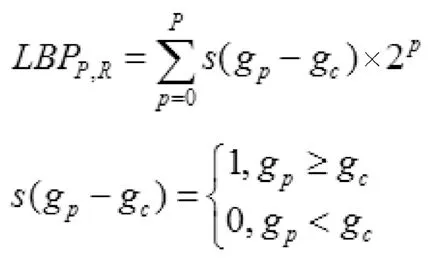
式中,gc的含义是窗口中心灰度,gp的含义是以窗口中心坐标为圆心,在半径R 的圆形区域之内的P 个像素灰度值,可知LBPP,R共有2P个不同的输出。
1.2.2 旋转不变性局部二值模式 针对目标图像可能旋转的情况,为了保持局部二值模式特征值的稳定,一些研究[8-10]对其进行了完善,以具有旋转不变特征的LBPriP,R替代传统的LBPP,R,表示为:

LBPriP,R可以理解为把目标像素的邻域依次旋转360 度后,提取出一系列LBPP,R,将其中的最小值作为邻域LBPriP,R。并且该研究还证实:LBPriP,R中的很多模式对纹理特征影响很微弱,因此将其中决定着目标纹理特征的主要模式命名为“均匀模式”,在大部分场合,仅需以“均匀模式”来描述目标的纹理。
依旧设像素点个数为P,窗口半径是R,局部二值模式算子的值由0 →1 或由1 →0 改变次数表示为:
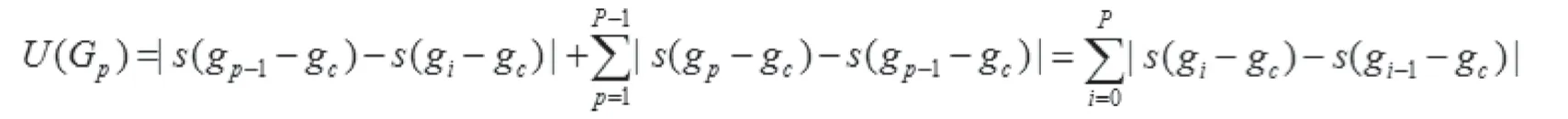
上式中,gP=g0,凡是符合U ≤2 的全部模式均视为均匀模式,表示为LBPU2P,R。为均匀模式植入旋转不变属性,并命名为LBPriu2P,R,称为“等价模式”表示为:
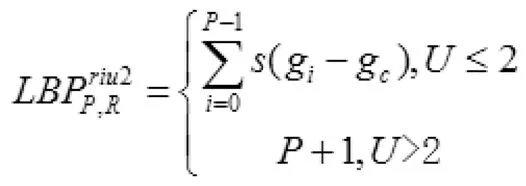
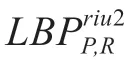

式中,n 的含义是局部二值模式算子的取值数目。
1.3 优化的局部二值模式
作为1 种描述纹理特征的方法,局部二值模式拥有不少优势,首先是描述图像特征的算法复杂度低,在设置窗口对目标图像进行遍历时仅涉及到比较运算及位移,所以能够保持特征描述的高效性;其次是局部二值模式不需要任何参数,不涉及参数寻优操作。但由局部二值模式的提取方法可知,该方法存在一些不足之处:
(1)局部二值模式共计2P个,而通常目标图像中的像素个数远多于2P,因此很多像素点即使其邻域像素分布存在很大差异,其局部二值模式却是互相重复的。
(2)局部二值模式关注的是目标图像中的中心像素与邻域像素之间的灰度关系,并未考虑邻域像素在分布上的特点,导致一部分纹理特征未能被有效提取。
本研究在优化算法中,在局部二值模式算子中,将目标图像邻域点灰度值间的关系加入进来[11]。具体实施思想为:
(2)当一轮比较结束之后,会得到0、1 序列值的比较结果,再对这些0、1 序列值进行编码。
优化算法具体实施思想体现为图2。
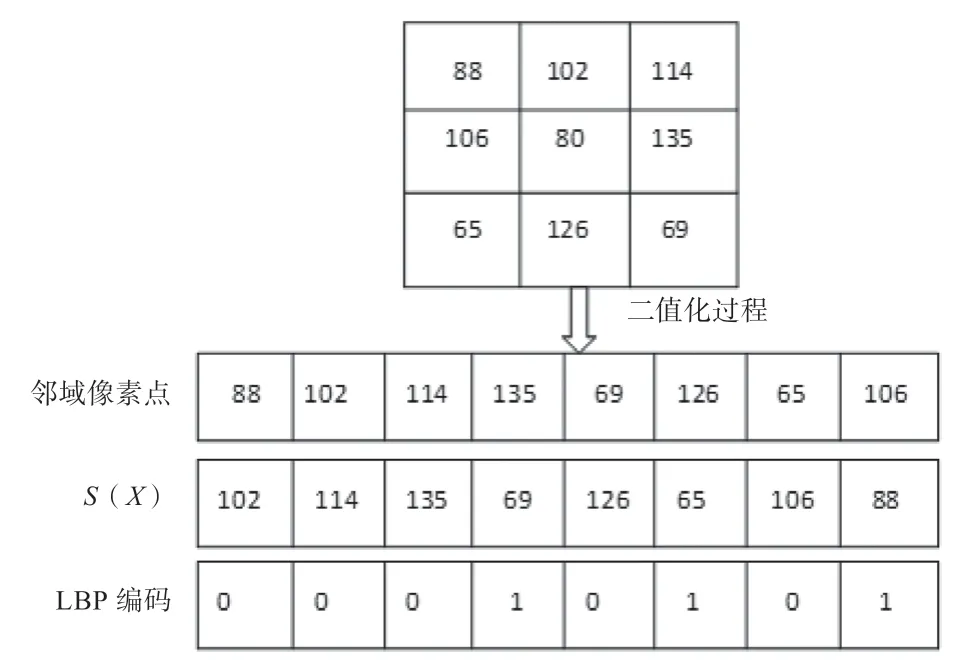
图2 改进算法示意图(P=8,R=1)Fig.2 Schematic of the improved algorithm (P=8, R=1)
优化算法所提取的纹理特征可以表示为:
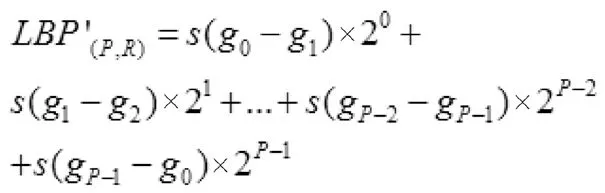
由此可知,将中心点周围的邻域点考虑进来是优化算法最大的特点。将基于传统模式的纹理特征图像,与优化后的局部二值模式取得的目标图像特征,两者相互结合,作为最终得到的目标图像特征。
2 中草药鉴别
结合所提取的颜色特征和纹理特征,对中草药截面切片显微图像进行鉴别。
2.1 相似性度量
常见的直方图相似性度量方法包括相交距离法、对数似然法等等[12]。本研究最终选择了这种方法,重要的原因是Chi 平方统计法对训练样本的数目要求较低。其原理为:以Am×h1表示训练集特征矩阵,其中m 的含义是训练集图像数量,hl的含义是特征向量所含有的维数;以Bn×h2表示测试集特征矩阵,其中n 的含义是测试集图像数量,h2的含义是特征向量所含有的维数;训练集成员i 和测试集成员j 的Chi 距离以Cij 表示,则相似性度量的流程可以体现为图3:
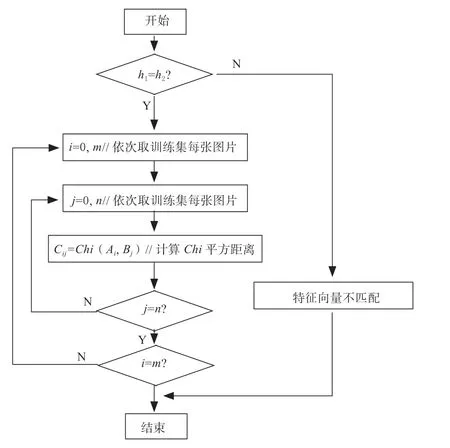
图3 相似性度量流程Fig.3 Similarity measurement process
2.2 基于改进K 近邻法的分类识别
引入K 近邻法对图像进行分类识别[13]。这种分类方法不必事先考虑目标图像的属性分布,且不需求取识别目标中的显式规则,因此效率和准确率均较高。
深秋已到,雁群南飞,凉风阵阵。一天,杨力生去二里地外一个镇上赶集,在集上,见有人卖新鲜牛肉,便随意买了四斤。他想,自己把这四斤牛肉一分两份,自己留下二斤拿回家,另外二斤便送给父母,让父母也尝尝鲜牛肉的味道。忽然想起媳妇与父母的矛盾。心想:这事要是让杨秋香知道,肯定两口子又要大吵起来,无奈,只得背着杨秋香把二斤牛肉送给了父母。不料,这天杨秋香到吴玉梅家和几个女伴玩扑克,到中午,正从另一条胡同回家,走到胡同口时,远远便看到杨力生提着二斤牛肉进了公婆的家,而杨力生却未看见她。回到家后,杨秋香心里的怒气不打一处来,脸拉得有二尺长,歪着头质问杨力生:“杨力生,你今天是不是送牛肉给你爹妈了?”
传统的K 近邻法流程如下:
(1)对待分类目标x 进行预处理,使其格式与训练集一致;
(2)结合相似性度量方法,获取分类目标与训练集之间相似度,将其中与待分类目标相似度较高的K 个成员当做分类目标x 的邻居成员;
(3)结合K 个邻居成员,为分类目标x 决定其具体类别。假设共计J 个类别,结合分类目标x 的K 个邻居,获取每个类别的可能性,方法为:

式中,wa(ai, Cj) 表示根据分类目标x 的邻居ai,把该目标划分为Cj类别的可能性。
传统的K 近邻法会面临“多优解”问题,对识别准确率造成影响[14]。本文对传统算法进行优化,主要思想是:将最短距离引入到K 近邻法中,对最优解进行整体判断。研究证实基于K 近邻法的分类出现多个不同结果时,距离最小的类别与目标所属类别之间相似度最高[15]。因此本研究将距离的远近作为在出现多个概率相等类别的情况下的最优解判断标准。当K 近邻法获取的K 个成员中会存在若干多优解,则最优解是距离最小的成员,这样会为该成员赋予更高的权重,从而相应减少距离最大的成员权重。具体的处理流程为:
(1)提取基于K 近邻法的分类作为最优解;
(2)判断该最优解是否是唯一解。倘若是,则将其作为最优解,并结束算法;
(3)在最优解中寻找距离最小的最优解,将其权重值加1;
(4)在最优解中寻找距离最大的最优解,将其权重值减1;
(5)将(3)—(4)循环往复,为所有的多优解排序,最终选择距离最小,也就是权重最大的解作为最优解。
3 实验结果与分析
3.1 实验方案
选取中草药图像数据库里的图像共计10 幅,包含6 个类别(中麻黄、木通、鸡血藤、北沙参、夜交藤、小蓟),对本文的分类方法进行验证和分析。原图大小均为960×960,等份切割后变成192×192,共计250 幅。为了对算法进行训练,每个类别随机抽取10 幅,共计100 幅,而其余的150 幅为测试集。先对所有的样本以颜色直方图形式进行初步的分类,再分别以传统的K 近邻法及本文优化K 近邻法,设置不同的K 值(1 ~10)进行分类,考察不同情况下的识别率,从而验证算法的效果。部分切割后的图像如图4 所示。
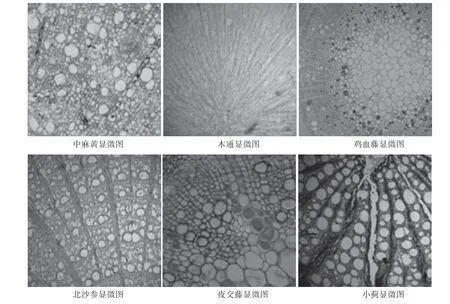
图4 部分切割后的待识别图像Fig.4 Image to be identified after partial segmentation
将训练集与测试集两者相结合,从而验证本算法在中草药横截面显微图像识别方面的具体性能。
实验环境如下:
戴尔OptiPlex,PIV CPU 3.0G,4GB RAM,操作系统Windows8,MATLAB 7.10.0。
主要验证的方面包括:
(1)验证对比本文的优化局部二值模式算法与传统算法对于中草药显微图像的识别率,计算方法为:

(2)验证适合中草药显微图像识别的最优K 值。对于K 的取值目前并不存在标准的确定方法,本文结合文献[16-19],以及本研究的训练集和测试集中所含有的样本数目,将K 设置在区间[5,50]。
(3)验证对比本文的优化算法与传统局部二值模式算法在运算时间上的性能。
当K 值分别取5、10、15、20、25、30、35、40、45、50 时,以本文改进后的K 近邻法,对局部二值优化方法与传统局部二值模式在识别率、识别时间上的测试结果进行比较。
3.2 实验结果
相关实验结果数据体现在表1。
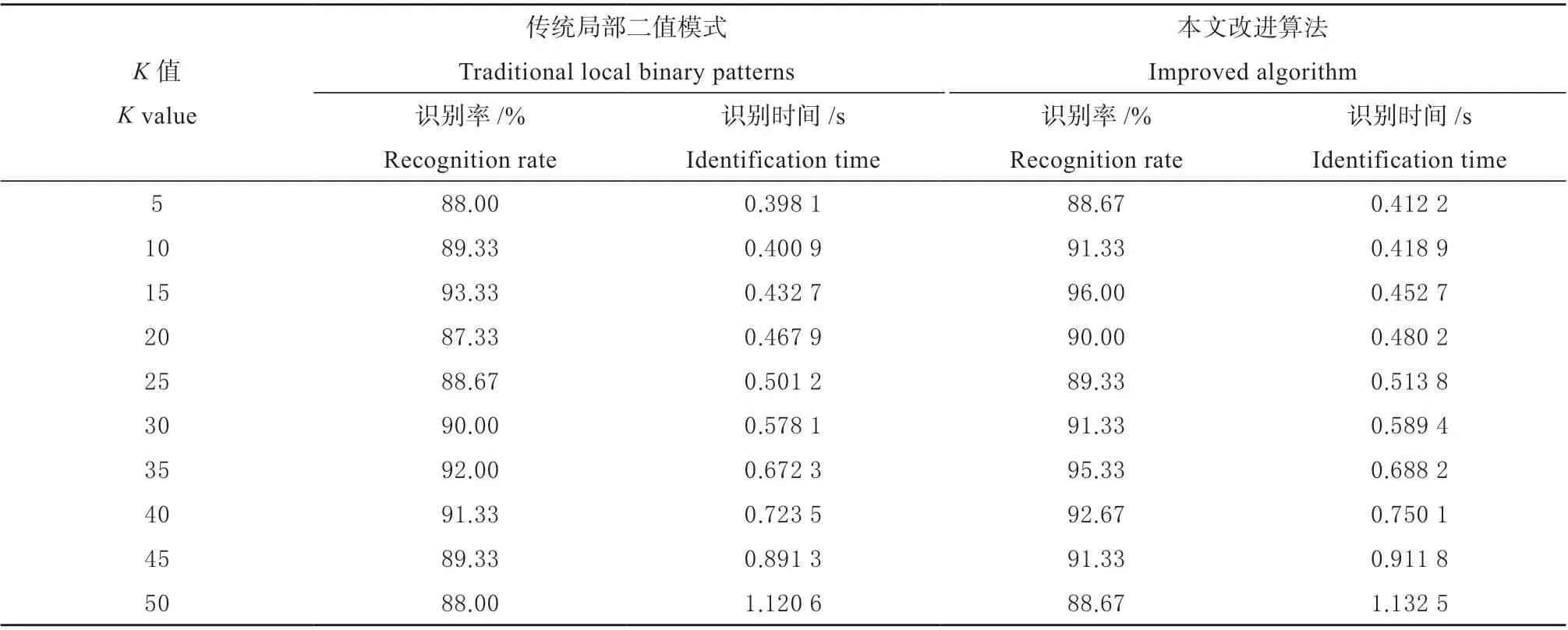
表1 不同K 值及不同算法在识别率和识别时间上的对比Table 1 Comparison of different K values and different algorithms in recognition rate and recognition time
不同K 值下的传统算法与本文优化算法在识别率上的比较如图5 所示。
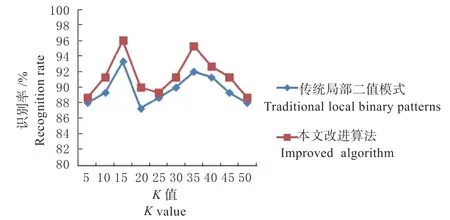
图5 不同K 值下的识别率比较Fig.5 Comparison of recognition rates under different K values
不同K 值下的传统算法与本文优化算法在识别时间上的比较如图6 所示。

图6 不同K 值下的识别时间比较Fig.6 Comparison of recognition time under different K values
3.3 结果分析
(1)从表1 及图5 的数据及曲线可看出,在中草药截面切片显微图像识别率方面,在K 取各个值的情况下,本文优化算法均高于传统的局部二值模式算法,最高识别率达到96.00%。传统的局部二值模式算法主要考虑的是中心点和领域的灰度关系,本研究是基于传统算法的基础上,考虑了领域像素的分布差异,并完善地体现出目标图像的全部纹理特征,提高了算法的性能,对于邻域点间关系的描述有所增加,这样在原有的基础上,保留了更多包含目标图像的有用信息,获得了更多纹理特征,比较原来的图像分类,取得了更明显的效果。
(2)从表1 及图5 的数据及曲线还可看出,无论是传统算法还是改进算法,K 的取值不同,识别率也有所不同。整体趋势为:K 值在[5,15]区间递增时,识别率呈现上升趋势,传统算法最高达到93.33%,优化算法最高达到96%;K 值在[15,25]区间递增时,识别率呈现下降趋势;K 值在[25,35]区间以及[35,50]区间递增时,识别率又分别呈现上升和下降趋势。K 值的选择是十分关键的,但目前的相关研究均是以不断调整试验的方法决定K 的最佳取值。由曲线图可知在K=15 及K=35 时,可以达到较好的分类效果。本研究经过对比,最终将K 的最佳取值定为K=15。
(3)从表1 及图6 的数据及曲线还可看出,当K 值确定的时候,本文的改进算法在识别时间上均略高于传统算法。当K=50 时,识别时间达到1.132 5 s。但整体来看,时间增加得并不多,因为为了提升识别准确率而稍微降低算法效率是值得的。总体而言,本研究所构建的优化识别算法是可行而有效的,对中草药显微图像的识别能够取得较为满意的效果。
4 结论
本文综合考虑中草药目标图像颜色特征和纹理特征,并结合中草药图像识别的需求,提出了更完善的识别方法。针对纹理特征对于旋转不变性的要求,在局部二值模式算法的基础上,进行改进,完善了特征的提取。改进了传统K 近邻分类法,使之避免陷入多个最优解,通过实验给出了较理想的K值。最后通过实验验证了本文算法的性能提升。本文的成果能够为中草药信息化建设和发展提供支持,在一定程度上推动中医中药产业化发展。

