大椭圆轨道SAR滑动聚束模式设计及斜距模型

李立， 李财品， 何明一

(1.西北工业大学 电子信息学院，陕西，西安 710129； 2.中国空间技术研究院，陕西，西安 710072)

大椭圆轨道SAR由于轨道偏心率大，在远地点附近相对运动缓慢，可视时间长，可提供高仰角优势，适合于针对特定高纬度区域长时间连续侦察监视. 另外，大椭圆轨道SAR卫星同时具有低轨详查与中高轨普查监视的特点，在近地点可实现高分辨成像，在远地点可长时间连续监视敏感地区，在未来军事和民事侦察领域具有重大应用潜力.

在现有的星载SAR卫星中，无论是处于低轨、中轨或者高轨[1-3]，其一般运行在圆形轨道上. 各种不同的成像模式都是在圆形轨道下提出的. 在圆形轨道上，其星下点高度在全轨范围内基本处于一致的高度. 因此其在全轨范围内成像模式的参数基本上是一致的. 然而在大椭圆轨道SAR下，其时变的轨道高度变化及时变多普勒特性造成了工作模式设计的特殊性. 如不同轨道位置处对观测目标的功率孔径不同，不同轨道位置处对分辨率改善因子不同，特殊的轨道特性造成了方位向多普勒特性随时间变化，不同轨道时间内波束地面覆盖足迹大小不一致等问题，因此在雷达系统工作模式设计时需要进行考虑.

另外，在大椭圆轨道下，其存在大的偏心率，星地相对运动轨迹严重偏离直线模型，斜视等效距离历程的拟合精度严重下降，并且常规的二阶斜距模型并不能用来描述大椭圆轨道SAR. 因此，需要建立更加合理的等效距离历程和点目标传递函数.

国内外在轨SAR卫星均处于圆轨道或者近圆轨道上，对大椭圆轨道SAR研究尚处于起步阶段，文献[4]建立了同步轨道合成孔径雷达(GEOSAR)的椭圆轨道模型,对其特殊的运动特性进行了分析,重点研究了椭圆轨道条件下目标的多普勒特性. 文献[5]开展了椭圆轨道全零多普勒导引律研究，提出一种基于椭圆轨道的全零多普勒方法,并用TerraSAR-X轨道参数进行了数值仿真,使用该方法后,多普勒中心频率被减小到不超过5 Hz. 文献[6]利用椭圆轨道下多普勒中心频率的表达式,将多普勒中心频率分为仅与俯仰角相关部分,以及与俯仰角和偏航角都相关的部分,残余多普勒中心频率约为0.03 Hz. 文献[7]给出了椭圆轨道GEO SAR非正交二维分辨率的评估方法，并且提出了利用连续变重频来解决椭圆轨道GEO SAR时变轨道高度带来的接收回波延迟变化的问题.

然而，上述的研究的椭圆轨道均属于小偏心率及远地点、近地点高度差别不大的轨道，国内外对于真正大椭圆轨道SAR的研究鲜有报道，对大椭圆轨道的工作模式设计更是未见公开报道.

本文对大椭圆轨道SAR轨道特性分析进行分析，包括空间几何关系、轨道高度变化、卫星速度变化情况等，在此基础上进行大椭圆轨道SAR滑动聚束工作模式设计，包括：不同轨道位置天线波束宽度要，天线扫描速度、扫描角速度等，对大椭圆轨道SAR滑动聚束模式的回波模型研究，考虑非停-走-停模型、多阶斜距模型对斜距表达式的影响.

1 大椭圆轨道SAR特性分析

1.1 空间几何关系

为了精确进行描述，需要对涉及到的空间坐标进行分析. 利用这些坐标系之间的平移和旋转关系，可以方便的对星载SAR星地相对运动状态、距离历程模型进行描述. 常用的7个空间坐标系[8]包括：大地坐标系，转动地心坐标系，不转动地心坐标系，卫星轨道坐标系，卫星平台坐标系，卫星星体坐标系以及天线坐标系. 这些坐标系可以通过一定的关系进行相互转换.

大椭圆轨道SAR采用如下仿真参数，远地点高度20 000 km，近地点高度1 000 km，轨道倾角63.4°，升交点赤经90°，近地点幅角270°，真近点角0°. 可得到大椭圆轨道SAR的空间几何关系如图1所示.

在卫星运行于不同的轨道段时，由于轨道的高度不同，导致了点目标完全不同的斜距历程，不同的斜距历程造成了成像处理严重的空变性，这极大增加了成像处理的难度.

另外，按照轨道参数可得到卫星轨道高度变化如图2所示.

1.2 地面波束足迹

设t时刻天线波束中心的地面投影在天线坐标系下的坐标为[0，r，0]T，式中r为标量，是天线相位中心到地面波束中心的距离.

地球采用椭球模型，地球赤道半径Re=6 378.137 km，地球极半径Rp=6 356.752 km，则在地心惯性坐标系下，地球椭球方程为

(1)

设0时刻卫星经过轨道的近地点，则t时刻对应的卫星真近心角为f. 设天线相位中心与卫星本体的质心重合，即[xa,ya,za]T=[0,0,0]T. 要求解r，可将地面波束中心的坐标[0，r，0]T由天线坐标系转换至地心惯性坐标系，再利用其满足地球椭球方程解得. 求得r后，即可得地面波束中心在地心轨道坐标系下的坐标.

按照轨道参数得到单轨的卫星地面波束足迹如图3所示，其中下视角为6°，俯仰向波束宽度为8°.

可见，在一定的视角下，在不同的纬度区域天线波束宽度对应的成像测绘带宽度不一致，因此需要根据不同轨道位置处所能达到的成像测绘带来确定成像的距离空变性. 另外，观察地面的波束足迹可知，在靠近远地点的位置处出现了两个波束足迹的拐点，这两个拐点将出现多普勒特性的变化.

1.3 变速运动

根据万有引力定律，卫星速度与空间几何关系、轨道高度之间具有耦合性和关联性，并且与轨道时间等因素有关. 通过坐标系转换，相对矢量信息及轨道时间可建立三者之间的关系[9]，下面直接给出相关的结论. 假设卫星的位置矢量rs、卫星速度Vs、目标的位置矢量rt，地球自转速度为Vt均已知.

则卫星相对于地面的速度为

(2)

β为卫星位置矢量rs与目标位置矢量rt地心夹角.

因此，可进一步得到波束地面速度为

(3)

按照轨道参数得到卫星全轨相对地面速度和波束足迹速度如图4所示.

大椭圆轨道SAR卫星相对地球速度与卫星波束足迹速度在全轨不同位置处存在较大的差别，在近地点较小而在远地点速度的差别更大. 由于在远地点位置处卫星波束足迹速度远比卫星相对地球速度慢，因此波束足迹驻留地面的时间更长，带来了更好的方位分辨率改善.

2 椭圆轨道SAR滑动聚束模式设计

在大椭圆轨道SAR下，其时变的轨道高度变化及时变多普勒特性造成了工作模式设计的特殊性. 如不同轨道位置处对分辨率改善因子不同，特殊的轨道特性造成了方位向多普勒特性随时间变化，从而造成了图像分辨率随着不同多普勒特性变化，固定雷达波束情况下地面波束足迹随时间出现变化等.

滑动聚束模式方位向分辨率如式(4)所示.

(4)

式中：Da为方位向发射天线尺寸；Vg为波束地面运动速度；Vs为卫星运动速度；γ为由于轨道高度带来的分辨率改善因子.

目标照射时间Ts如下式所示，其中R为目标至场景中心斜距，可见，目标照射时间与方位分辨率及平台飞行速度有关.

(5)

天线波束角扫描速度为

(6)

设天线方位向波束扫描的角度范围为θ∈[θstart,θend]，且定义Δθ=θend-θstart，则方位向成像场景总宽度为

(7)

大椭圆轨道SAR下，由于其轨道高度不断变化，如果采用固定的波束宽度照射，其天线3 dB测绘带不同，下面分析波束照射范围.

假设卫星天线俯仰向波束宽度为βa，在t时刻卫星星下点地理坐标系纬经度及高度为(Ln,λn,Re)，星下点速度为(vx,vy,vz)，其矢量表达为vse，由于雷达正侧视工作时雷达波束始终垂直于卫星速度方向，设经过星下点且与vse垂直的落在波束平面内的向量为vb，如图5所示.

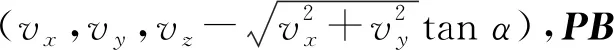
(9)

式中：xA,yA,zA分别为点A在地球直角坐标系中的坐标；xP,yP,zP分别为点P在地球直角坐标系中的坐标；vx_PA,vy_PA,vz_PA分别为向量PA在地球坐标系中x,y,z轴的投影.

同理也可以得到B点在地球直角坐标系内坐标为

式中xB,yB,zB分别为点B在地球直角坐标系中的坐标，xP,yP,zP分别为点P在地球直角坐标系中的坐标.vx_PB,vy_PB,vz_PB分别为向量PB在地球坐标系中x,y,z轴的投影. 点A和点B所围成的区域就是大椭圆SAR俯仰向波束照射范围.

随着卫星轨道高度的变化，固定波束照射范围也随着高度变化. 针对这个问题有两种技术途径可以采用，一种是通过雷达采样窗回波信号进行截取来获取一定的测绘带，例如如果天线波束宽度的3 dB对应的幅宽很宽，超过了任务要求的测绘带宽度，那么可以通过雷达采样窗回波信号来截取的天线波束宽度，这样能够使得波束边缘获得更好的天线增益，然而这种方法这是能够对波束边缘天线增益的获取有好处，而且还需要根据轨道高度的变化进行合理的选取，如果长时间对不同天线波束宽度进行截取还容易导致一副图像辐射强度的不一致. 因此，需要进行合理的采样窗回波信号截取准则来保证雷达的图像质量.

另外一种技术途径是随着大椭圆轨道高度的提升如果需要波束中心获得较好的天线增益，那么就不能通过截取回波窗口了，而是应该根据不同的任务需求及其不同的轨道高度对天线波束宽度及其增益进行调整，通过降低波束宽度，提高天线增益，以获得较好的系统灵敏度及图像信噪比.

3 滑动聚束斜距模型

在滑动聚束成像回波模型中，传统低轨SAR普遍采用了“停-走-停”假设,即收发脉冲期间平台位置的移动可以忽略. 然而，大椭圆轨道远地点平台到目标距离远，回波时延大幅增加，在这期间平台的移动不能忽略，因此大椭圆轨道SAR不再满足“停-走-停”假设. 传统SAR斜距模型普遍采用二阶斜距模型，低轨SAR卫星的合成孔径时间短，只有数秒钟的时间，在该照射时间范围内，可认为“停-走-停”假设模型几何关系仍然成立[10]. 然而，大椭圆轨道SAR远点段合成孔径时间为百秒量级，回波时延大幅增加，传统斜距模型不再适用，需要特别分析.

3.1 非停走停模式分析

大椭圆轨道SAR最长的回波时延长达百ms量级，在如此长的时间范围内，由于卫星运动使得雷达信号发射与接收位置不能简单看成同一位置，即常规低轨及机载SAR的“停-走-停”模式不再适用于大椭圆轨道SAR.

下图显示了非“停-走-停”假设下目标与平台几何关系，其中tstart为雷达信号发射信号时刻(为已知量)，tend为雷达信号接收时刻(为未知量)，O为目标位置. 设卫星和点目标在地球固定坐标系下的位置矢量分别为RS和RT，则在发射时刻卫星位置为RS(tstart)，接收时刻卫星位置为RS(tend)，点目标位置为RT(tstart)，则

tend=tstart+

(11)

tend的值可以由方程(11)求出.

3.2 斜距表达式分析

将斜距进行泰勒级数展开并表示成标量形式[11-13]

(12)

式中：

RST=RS-RT,VST=VS-VTAST=

AS-ATBST=BS-BT,

RS,VS,AS,BS分别为波束中心时刻卫星位置矢量一阶、二阶、三阶导数，RT,VT,AT,BT分别为波束中心时刻点目标位置矢量一阶、二阶、三阶导数.

假设雷达发射线性调频信号，回波经过解调后的信号模型可以表示为[14]

s0(tr,ta)=

(13)

式中：tr为距离向时间；ta为方位向时间；wr为距离向包络；wa为方位向包络；f0为雷达中心频率；Kr为距离向信号调频率；c为光速；R(ta)为目标点到卫星瞬时斜距.

4 仿真验证

为了对大椭圆轨道SAR滑动聚束模式进行仿真验证，选取以下仿真参数如表1所示.

表1 仿真参数Tab.1 Simulation parameters

根据以上的仿真参数，进行大椭圆轨道SAR模式设计，首先需要考虑到在不同轨道高度下，波束地面足迹速度与卫星相对地面速度不同差异带来的分辨率改善因子不同[15]，如图7所示.

然后，根据分辨率及成像覆盖需求计算天线波束要求. 假设成像模式要求的方位向成像分辨率为0.3 m，方位向覆盖要求为10 km，根据这些参数可计算方位向波束旋转角度、波束旋转速率.

从图8可以看出，在0.3 m测绘带宽度为10 km情况下，20 m天线发射在近地点天线波束扫描为±9.2°，总共扫描角度为18.4°，在远地点位置处天线波束扫描±0.09°，总共扫描角度为0.18°.

根据不同轨道高度分析不同轨道高度及不同时间内波束足迹地面覆盖变化. 下面分别给出近地点2时刻间隔10 min地面波束足迹之间的变化,如图9所示.

可见，不同轨道高度造成了地面波束足迹的不一致，即造成了成像测绘带的变化，首先分析通过截取雷达回波信号长度的方式，即截取同一天线不同位置处的波束宽度，如图10所示.

由此可见，当天线的增益由峰值下降3 dB变为下降2.5 dB时,天线波束宽度变窄约为原来的91.6%. 当天线的增益由峰值下降3 dB变为下降2 dB时,天线波束宽度变窄约为原来的82.52%. 当天线的增益由峰值下降3 dB变为下降1 dB时,天线波束宽度变窄约为原来的59.05%. 因此，如果要将一副图像的增益变化控制在0.5 dB范围之内，通过雷达采样窗回波信号进行截取的方式只能在原波束宽度的91.6%进行截取.

另外，也可以实时调整天线3 dB波束宽度，对于大椭圆轨道来说，由于轨道高度是时变的，同样的测绘带其所需要天线俯仰向波束宽度也不一样,如图11所示.

通过采用上述两种方法后，天线波束在地面的足迹如图12所示，获得了一致的地面波束覆盖.

综合以上的分析，大椭圆轨道SAR滑动聚束模式设计流程可用如图13表示.

以大椭圆轨道过近地点1,2和3 h为例，对回波的双程斜距进行仿真分析，其目标位于场景中心点位置. 下图左侧为非“停-走-停”假设下精确计算的斜距，右侧为两种斜距之差. 从图14可以看出，“停-走-停”假设下引起的相位误差远远大于π/4，因此大椭圆轨道SAR必须采用非“停-走-停”模式，即收发分离计算.

下面分析斜距多斜展开模型的误差，图15分别为大椭圆轨道二阶和三阶斜距模型产生的斜距误差，从图中可以发现：当斜距模型取到三阶时，就可以满足大椭圆轨道斜距历程的精度要求.

由上面的仿真图可以看出，当斜距模型展开到三次时其斜距模型误差远远小于波长的1/16(3.4×10-3m)，从而引起相位误差小于π/4，能满足成像需求[16].

5 结束语

大椭圆轨道SAR具有在远地点附近相对运动缓慢，可视时间长，可提供高仰角优势，适合于针对特定高纬度区域长时间连续侦察监视. 另外，大椭圆轨道SAR卫星同时具有低轨详查与中高轨普查监视的特点，在近地点可实现高分辨成像，在远地点可长时间连续监视敏感地区，在未来军事和民事侦察领域具有重大应用潜力. 然而，大椭圆轨道SAR存在大偏心率、时变轨道高度及卫星速度时变的特性也造成雷达系统工作模式设计存在特殊性. 本文首次对大椭圆轨道SAR滑动聚束工作模式进行了设计，对大椭圆轨道SAR特性进行研究，包括空间几何关系、轨道高度变化、卫星速度变化情况等. 在此基础上进行大椭圆轨道SAR滑动聚束工作模式设计，包括:不同轨道位置天线波束宽度设计、地面波束足迹一致性设计、天线扫描角度、天线扫描角速度等. 最后对大椭圆轨道SAR滑动聚束模式回波斜距模型研究，考虑非停-走-停模型、多阶斜距模型对斜距表达式的影响. 希望本文对大椭圆轨道SAR的研究能够起一定的参考借鉴作用.